Obersumme Untersumme Zwischenwertsumme - Technik

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Numerische Methoden zur Lösung bestimmter Integralen
Da es oft schwierig oder sogar unmöglich ist, die Stammfunktion durch eine bekannte Funktion
auszudrücken, ist es oft sinnvoll/einfacher bestimmte Integrale numerisch zu lösen.
Ein bestimmtes Integral läßt sich durch Ober-, Unter- oder Zwischenwertsummen approximieren.
Dabei wird die Fläche eines Teilintervalls durch ein Rechteck approximiert. Für die Bestimmung
der Obersumme (Untersumme) wird als Rechteckhöhe im Teilintervall der Maximalwert
(Minimalwert) im Teilintervall angesetzt. Bei der Zwischenwertsumme wird der Funktionswert
4
für einen Zwischenwert (z.B. die Mitte) des Intervalls angesetzt.
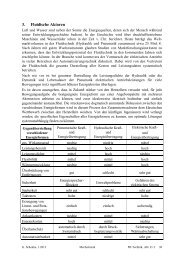
Die 3 folgenden Abb. zeigen die Ober-, Unter und Zwischenwertsumme zur Best. von x 2 dx
:
Obersumme
∫
0
Untersumme
Zwischenwertsumme
# Teilintervalle Fläche Untersumme Fläche Obersumme F. Zwischenwertsumme
4 14 30 21
16 19,39 23,37 21,31
256 21,21 21,46 21,33
3

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Die exakte mathematische Lösung für dieses Beispiel ist natürlich sehr einfach:
4
x 2 x 3 4
∫ dx
----
64
= = ----- = 21 1 3 0 3 3 --
0
Der Grenzwert für #Teilintervalle → ∞ strebt für alle 3 Summen gegen den Wert des tatsächlichen
bestimmten Integrals:
4
n
n
∫x 2 d x lim ∑
4 – 0
U i ⋅ -----------
n
O 4 0
n
lim ∑
–
⋅ ----------- i n → ∞ n
Z 4 –
= = = lim ∑ ⋅ -----------
0
i n → ∞ n → ∞ n
0
i = 1
i = 1
i = 1
Neben diesen 3 Verfahren gibt es folgende weitere Verfahren:
• Links- und Rechtssumme: ähnlich Unter-/Obersumme; jedoch wird anstelle des Max-/Min-
Wertes immer der linke bzw. rechte Funktionswert angesetzt - für obiges Beispiel entspricht
die Untersumme auch der Linkssumme und die Rechtssumme der Obersumme, da die Beispielfunktion
im Integrations-Intervall monoton steigt.
• Trapezsumme: Die Fläche für das Intervall [x i ;x i+1 ] wird durch ein Trapez angenähert. Die
fx ( i – 1
) + fx ( i
)
Teilfläche von einem Trapez ist gegeben durch A i
= ---------------------------------- ⋅ ( x
2
i + 1
– x i
)
• Simpson-Summe:
Beim Trapezsummen-Verfahren wird die Funktionskurve für ein Teilintervall durch seine Sekante
angenähert.
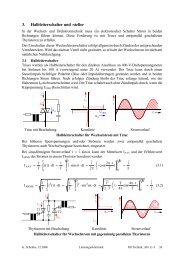
Bei der Simpson-Summe wird die Funktionskurve durch ein Polynom 2.Grades
( y = a 2 x 2 + a 1 x + a 0 ) für einen Doppelstreifen angenähert (siehe Abbildung). D.h., dass
das Polynom durch die 3 Kurvenpunkte P 0 , P 1 und P 2 von f(x) definiert ist. Der Flächeninhalt
A P1 zwischen dem Polynom und der x-Achse soll also den Flächeninhalt zwischen f(x) und
der x-Achse im Intervall [x 0 ,x 2 ] approximieren.
y
P 2
0
y 0
h h
x 0 x 1
x 2
f(x)
x
4

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Der Flächeninhalt A P1 läßt sich wie folgt berechnen:
x + 2h
∫
A P1
= ( a 2
x 2 + a 1
x+
a 0
) dx
=
x 0
⎛a 2
x 3 a
---------- 1
x 2 ⎞
⎜ + ---------- + a
3 2 0
x⎟
⎝
⎠
x 0
x 0
+ 2h
a 2 ( x 0 + 2h) 3 a
------------------------------ 1 ( x 0 + 2h) 2
3 2
a
------------------------------ 2 x 0
a
a
3
2
0
( x 0
+ 2h)
------------ 1 x 0
=
+ +
– – ------------ – a
3 2 0
x 0
3
a 2
x 0 2
------------ 2a
3 2
x 0h 4a2 x 0
h 2 8 2
3 --a 2
h 3 a 1
x 0
+ + + + ---------- + 2a
2 1
x 0
h + 2a 1
h 2 + a 0
x 0
+ 2a 0
h
=
3 2
a 2
x
------------ 0
a 1
x 0
– – ------------ – a
3 2 0
x 0
=
2
2a 2 x 0h + 4a2 x 0 h 2 + 8 3 --a 2 h 3 + 2a 1 x 0 h + 2a 1 h 2 + 2a 0 h
=
=
h 2
--( 6a
3 2
x 0
+ 12a 2
x 0
h + 8a 2
h 2 + 6a 1
x 0
+ 6a 1
h + 6a 0
)
⎛
2
h
a 2
x 0
+ a 1
x 0
+ a 0
--⎜
3⎜
⎝
⎧ ⎪⎪⎨⎪⎪⎩
+ 4
⎧ ⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩
y 0
2
⎛a 2
x 0
+ 2a 2
x 0
h + a 2
h 2
⎞
⎜
+ a 1
( x 0
+ h) + a ⎟
⎜
0
⎝ a 2 ( x 0 + h) 2 ⎟
⎠
⎧ ⎪⎪⎪⎨⎪⎪⎪⎩
+
⎧ ⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩
⎧ ⎪⎪⎪⎪⎪⎪⎪⎪
⎨
⎪⎪⎪⎪⎪⎪⎪⎪⎩
h
A P1 = --( y
3 0 + 4y 1 + y 2 )
Daraus folgt, dass man die Koeffizienten a 2 , a 1 und a 0 nicht bestimmen muss, um die Fläche
A P1 zu bestimmen. Analog zur Berechnung des Flächeninhalts A P1 können die Flächeninhalte
der Doppelstreifen A Pi berechnet werden:
A P2
Das zu approximierende bestimmte Integral I =
y 1
2
a 2 x 0 + 4a 2 x 0 h + 4a 2 h 2
⎞
⎟
+ a 1 ( x 0 + 2h) + a 0 ⎟
a 2 ( x 0 + 2h) 2 ⎟
⎟
⎟
⎠
h
--
h
= ( y
3 2 + 4y 3 + y 4 ) A P3 = --( y
3 4 + 4y 5 + y 6 )
h
A Pi = --( y
3 2i – 2 + 4y 2i – 1 + y 2i )
y 2
f( x) dx
soll nun durch die Aufsummierung
von n Doppelstreifen gebildet werden. Hierbei fällt auf, dass alle ungeraden Stützstel-
b
∫
a
5

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
len 4-fach in die Flächenbildung eingehen und alle geraden Stützstellen bei zwei
aufeinanderfolgenden Doppelstreifen je 1x (also insgesamt 2x) berücksichtigt werden (Ausnahme
erster und letzter Doppelstreifen). Das bestimmte Integral läßt sich also wie folgt
approximieren:
n
∑
i = 1
A Pi
h⎛
= --⎜
3⎝
⎧ ⎪⎨⎪⎩
⎧ ⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩
⎧ ⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩
y 0
+
S0
y 2n
I
=
b
∫
a
f( x) dx
≈ ∑
n
A Pi
i = 1
⎛ ( y 1
+ y 3
+ … + y 2n – 1
) ⎞ ⎛
+ 4⎜
⎟ + 2⎜
⎝
S1 ⎠ ⎝
( y 2
+ y 4
+ … + y 2n – 2
)
S2
⎞⎞
⎟⎟
⎠⎠
Sämtliche dieser Approximationsverfahren konvergieren für n → ∞ gegen den tatsächlichen
Integralwert. Erfahrungsgemäß konvergieren die verschiedenen Vefahren in folgender Reihenfolge:
• am schnellsten: Simpson-Summe
• Zwischenwertsumme
• Trapezsumme
• Unter-, Ober-, Links- und Rechtssumme
6

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Lösung komplizierter unbestimmter Integrale
Trignometrische Integrale
Enthalten die Integranden Produkte mehrerer trigonometrischer Funktionen oder zusammengesetzte
Funktionen mit trigonometrischen Funktionen, so kann man diese oft durch geschickte
Umformungen und Substitutionen lösen.
Beispiele:
∫
( cosx) 3 dx
∫
( sinx) 5 ( cosx) 2 dx
Wichtige trigonometrische Beziehungen für Umformungen:
( sinϕ) 2 + ( cosϕ) 2
sinϕ
= 1 tanϕ
= ----------- 1 + ( tanϕ) 2
cosϕ
sinα
sinα
cosα
⋅ cosβ
⋅ sinβ
⋅ cosβ
1
= -- [ sin( α–
β)
+ sin( α+
β)
]
2
1
= --[ cos( α–
β)
– cos( α+
β)
]
2
1
= --[ cos( α–
β)
+ cos( α+
β)
]
2
( cosϕ) 2 = 1 ------------------------
+ cos2ϕ
( sinϕ) 2 = ------------------------
1– cos2ϕ
2
2
( cosϕ) 3 = 3 -------------------------------------
cosϕ
+ cos3ϕ
( sinϕ) 3 =
3 -----------------------------------
sinϕ
– sin3ϕ
4
4
sinnϕ
=
∑
n
k = 0
n
⎛n⎞( cosϕ) k ( sinϕ) n– k n– k
⎝k⎠
sin ---------- π
⎝
⎛ 2 ⎠
⎞
cosnϕ
n
= ⎛ ⎞
∑ ( cosϕ) ( sinϕ) ---------- – k π
⎝k⎠
⎝
2 ⎠
k = 0
⎛n⎞ n!
= --------------------------
⎝k⎠
( n – k)! ⋅ k!
n! = n ⋅ ( n – 1) ⋅( n – 2)…3 ⋅ 2 ⋅ 1 0! = 1
1
= -------------------
( cosϕ) 2
( sinϕ) 2 ( cosϕ) 2 = 1 ------------------------
– cos4ϕ
( sinϕ) 3 ( cosϕ) 3 = ---------------------
( sin2ϕ)3
8
8
Weitere Strategien werden in der Vorlesung behandelt.
7

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Trigonometrische Grundintegrale
∫
fx ( ) Fx ( ) = fx ( ) dx
fx ( ) Fx ( ) = fx ( ) dx
∫
cosx
sinx
+ C
x
tan ln ----------
1
cosx
+ C
sinx
– cosx
+ C
cotx
ln
sinx
+ C
------------------
1
( cosx) 2
tanx
+ C
---------
1
sinx
ln
---------
1
+ cotx
sinx
+ C
-----------------
1
( sinx) 2
1
– ---------- + C = – cotx
+ C
tanx
----------
1
cosx
ln
----------
1
+ tanx
cosx
+ C
------------------
sinx
( cosx) 2
----------
1
+ C
cosx
-----------------
cosx
( sinx) 2
1
– --------- + C
sinx
Trignometrische Substitution
Für folgende Terme im Integranden bieten sich trigonometrische Funktionen zur Substitution
an:
Term im
Integranden
Substitution
Definitionsbereich
von ϕ
trignometrische
Beziehung zur
Vereinfachung
a 2 – x 2
x = a⋅
sinϕ
dx = a ⋅ cosϕ
⋅ dϕ
π
–--
≤ ϕ ≤ π 2
-- 1 – ( sinϕ) 2 = ( cosϕ) 2
2
a 2 + x 2
x = a⋅
tanϕ
dx
a
= -------------------
( cosϕ) 2 ⋅ dϕ
π
–--
< ϕ < π 2
-- 1 + ( tanϕ) 2
2
=
-------------------
1
( cosϕ) 2
x 2 – a 2
a
x = -----------
cosϕ
tanϕ
dx = a ⋅ ----------- ⋅ dϕ
cosϕ
0 ≤ ϕ <
π -- oder
2
π
-- < ϕ ≤ π
2
-------------------
1
( cosϕ) 2 – 1 = ( tanϕ) 2
8

Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
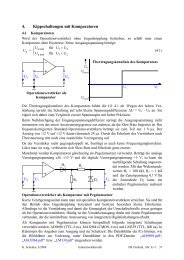
graphische Darstellung der o.a. Integranden:
x 2 – 4
4 + x 2
4 – x 2
9