Psychologische Diagnostik II - Universität Regensburg

Psychologische Diagnostik , latent trait Theorie
WS 2010/11
Prof. Dr. Jan Drösler
Universität Regensburg
Das diagnostische Gespräch
Hell u. a. (2007) haben knapp 4000 Validitätsuntersuchungen,
die seit 1980 berichtet worden
sind, ausgewertet. Es ergab sich (nach rechnerischer
Schönung der Daten wegen mangelnder
Reliabilität des jeweiligen Kriteriums) eine
mittlere Validität von rho = 0.12
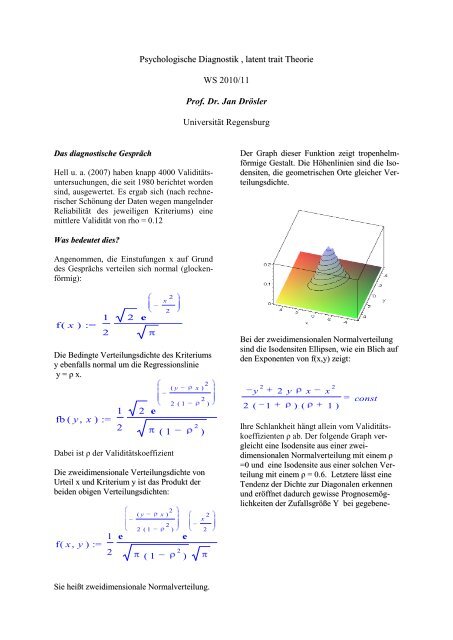
Der Graph dieser Funktion zeigt tropenhelmförmige
Gestalt. Die Höhenlinien sind die Isodensiten,
die geometrischen Orte gleicher Verteilungsdichte.
Was bedeutet dies?
Angenommen, die Einstufungen x auf Grund
des Gesprächs verteilen sich normal (glockenförmig):
x 2
f( x )
Die Bedingte Verteilungsdichte des Kriteriums
y ebenfalls normal um die Regressionslinie
y = ρ x.
Dabei ist ρ der Validitätskoeffizient
Die zweidimensionale Verteilungsdichte von
Urteil x und Kriterium y ist das Produkt der
beiden obigen Verteilungsdichten:
f ( x,
y )
:=
fb ( y,
x )
:=
1
2
:=
1
2
1
2
e
2 e
2 e
2
( y x )
2
2
2 ( 1 )
e
2
( 1 )
( y x )
2
2
2 ( 1 )
2
( 1 )
x 2
2
Bei der zweidimensionalen Normalverteilung
sind die Isodensiten Ellipsen, wie ein Blich auf
den Exponenten von f(x,y) zeigt:
Ihre Schlankheit hängt allein vom Validitätskoeffizienten
ρ ab. Der folgende Graph vergleicht
eine Isodensite aus einer zweidimensionalen
Normalverteilung mit einem ρ
=0 und eine Isodensite aus einer solchen Verteilung
mit einem ρ = 0.6. Letztere lässt eine
Tendenz der Dichte zur Diagonalen erkennen
und eröffnet dadurch gewisse Prognosemöglichkeiten
der Zufallsgröße Y bei gegebeney
2 2 y x x 2
2 ( 1 ) ( 1 )
const
Sie heißt zweidimensionale Normalverteilung.

nem Y = x.
Ein entsprechender Vergleich mit Validitäten ρ
= 0 und ρ = 0.1 (der Validität des freien Untersuchungsgesprächs)
lässt jede Prognosemöglichkeit
praktisch verschwinden:
Daraus ergibt sich für die Psychologie das
Gebot, freie Untersuchungsgespräche zu unterlassen
und statt dessen jede Diagnostik zu objektivieren.
Das kann beispielsweise durch die
Verwendung von Tests geschehen, in denen
der zu untersuchende Proband Punktwerte
erzielen kann. Das Grundproblem jeder auf
diese Weise objektivierten Diagnostik lautet:
Was bedeutet es, Punktwerte zu addieren?
Die Theorie der Diagnostik
stellt, Objektivität und Reproduzierbarkeit
der Befunde sicher. Definition eines Entscheidungsraums.(Befund
„wofür“). Sie
definiert Validität der Befunde im Hinblick
auf ein Kriterium (Punktwert bedeutet das
und das). Wenn also eine Universität vom
Bertelsmann-Intitut CHE einen höheren
Rangplatz auf Grund einer höheren Punktzahl
bekommt, so müßte damit irgendeine
Bedeutung verbunden sein, die eine Universität
auszeichen könnte. Infrage käme,
daß etwa ihre Absolventen mehr verdienen,
seltener arbeitslos sind oder umfangreichere
Fachkenntnisse besitzen als die
Absolventen anderer Universitäten. Das ist
aber ebenso wenig der Fall wie der Nachweis
irgend einer anderen nennenswerten
Bedeutung. Die von der Illustrierten Stern
verbreiteten Punkwerte sind bedeutungslos.
Ihre Sinnlosigkeit läuft auf eine Desinformation
der öffentlichkeit hinaus.
Grundsätzlich stehen drei Wege offen, die
Äquivalenz von Versuchspersonen mit
gleicher Punktzahl zu untersuchen. Der
einfachste Weg ist die Korrelation der
Punktwerte mit einem nahe liegenden Außenkriterium.
Diesen Weg geht die klassische
Testtheorie. Ein zweiter Weg besteht
in der Untersuchung der empirischen
Struktur und deren Vergleich mit den Bestimmungsstücken
einer Zahlenstruktur.
Diesen Weg geht die repräsentative Meßtheorie.
Ein dritter Weg ist der statistische.
Es wird untersucht, ob beispielsweise die
Punktsummen erschöpfend über einen dahinterliegenden
latent trait Auskunft geben.
Dieser Weg wird din dieser Vorlesung
im Einzelnen beschritten.
Optimalität
Den Befunden soll die Bedeutung nicht
beliebig sondern in optimaler Weise zugeordnet
werden. Das setzt einen Bewertungsmaßstab
sowie außerdem ein Optimalitätskriterium
voraus. Voraus-setzung für
deren Erstellung ist die Objektivität der
Befunde. Sie ist wie folgt definiert: Die
Wahrscheinlichkeit des Auftretens eines
Befundes hängt nicht vom Untersucher ab.
Für die Erhebung jedes Befundes muß
schon aus diesem Grunde ein Wahrscheinlichkeitsraum
definiert sein:
< , , >
Dabei ist die Ergebnismenge, z. B.
{Aufgabe gelöst, nicht gelöst}.die Ereignismenge,
z. B.{ Aufgabe gelöst oder
nicht gelöst, Aufgabe gelöst, nicht gelöst,

Aufgabe gelöst und nicht gelöst}, das
Wahrscheinlichkeitsmaß (nicht-negativ,
normiert, additiv) auf der Ereignismenge.
Der Entscheidungsraum
Nach diesen Vorüberlegungen lässt sich
die Validitätsfrage systematisch untersuchen.
Befunde x werden, wie gesagt, nicht
isoliert betrachtet. Sie sollen Indikatoren
für etwas anderes sein, das Kriterium . In
einem wissenschaftlichen Kontext ist diese
Beziehung empirisch nachzuweisen: Die
Frage lautet:
P( x | ) = P( x ) ?
Erst wenn diese Frage verneint werden
kann, geht es um die Findung einer Diagnose
(als einer optimalen Entscheidung).
Optimalität der Entscheidung
Optimalität verlangt zweierlei: einen Kostenmaßstab
und ein Optimalitätskriterium.
Im vorliegenden Zusammenhang wird der
Erwartungswert der quadrierten Größe der
Abweichungen vom Kriterium als Maßstab
benutzt. Als Optimalitätskriterium
dient die maximale Likelihood.
Likelihood
Folgen die Daten X einer diskreten Zufallsverteilung,
dann ist pk die Wahrscheinlichkeit
für das Eintreffen von
X = xk, k = 1,2,3 ..., n, und , unbekannte
Parameter. Hier ist
L = p1( , ) p2( , ) p3( , )... pn( , )
die Likelihood. Diese Produktbildung setzt
voraus, daß die einzelnen diagnostischen
Ereignisse pk voneinander stochastisch
unabhängig sind. Andernfalls wäre die
Likelihood viel komplizierter zu formulieren.
Für die psychologische Diagnostik
bedeutet dies beispielsweise, daß die Versuchsperson
aus den früheren diagnostischen
Zugriffen nicht in der Weise lernen
darf, daß es ihr späteres Verhalten in der
gleichen Untersuchung verändern würde.
Für kontinuierlich zufallsverteilte Daten ist
die Likelihood entsprechend als das Produkt
der Dichten für die einzelnen Ergebnisse
definiert und deshalb keine Wahrscheinlichkeit.
Maximum Likelihood
Funktionen kann man, wie in der 11.
Gymnasialklasse unterrichtet wird, durch
Ableiten und Nullsetzen der Ableitung
optimieren. Das setzt voraus, daß man die
Wahrscheinlichkeit für das Auftreten der
Daten explizit formuliert hat, also eine
Theorie für die Entstehung der Daten besitzt.
Ein Beispiel für eine solche diagnostische
Theorie ist das Rasch-Modell.
Das Rasch-Modell
Sei U = 0,1 eine Zufallgröße, und ,
Parameter, i der Personenindex, j der Aufgabenindex,
dann ist die Lösungswahrscheinlichkeit
PU ( 1 | , )
i.
j i j
exp( )
1 exp( )
Die Lösungswahrscheinlichkeit einer Aufgabe
hangt entsprechend der logistischen
Funktion von der Differenz von Personenfähigkeit
und Aufgabenschwierigkeit ab.
Sind beide gleich, so ist das Argument der
Funktion gleich null und der Funktionswert
gleic ½. Der Fähigkeitswert, bei dem dieser
Funktionswert auftritt, ist der Zahlenwert
der Aufgabenschwierigkeit.
i
i
j
j

Die Aufgebencharakteristik
Die Likelihood-Funktion
Sei U = 0,1 eine Zufallgröße, und ,
Parameter, i der Personenindex, j der Aufgabenindex,
dann ist die Wahrscheinlichkeit
als Likelihood-Funktion für eine Aufgabe
und eine Person zum Rasch-Modell
gegeben.
P ( U u | , )
i. j i , j i j
exp[ u ( )]
i , j i j
1 exp( )
Die Versuchsperson als Zufallgenerator
i
j
Die Aufgaben-Charakteristik verläuft als
logistische Funktion von (θ- ) ogivenförmig.
Andere Ogiven
Die Formel des Rasch-Modells legt in Abhängigkeit
von Personenfähigkeit und
Aufgabenschwierigkeit eine Wahrscheinlichkeit
fest, mit der richtige bzw.
falsche Lösungen produziert werden. Diese
werden als Einsen bzw. Nullen kodiert.
Bei gegebener Aufgabe wird die Wahrscheinlichkeit,
bei einer Vp. mit großer
Fähigkeit hoch sein, aber nicht den Wert
Eins annehmen.
Aufgabe des Diagnostikers
Die Aufgabe des Diagnostikers besteht
darin, aus den zufälligen Nullen und Einsen,
dem Antwortmuster, die Werte von
und zu erschließen und Angaben über
die Genauigkeit dieses Verfahrens zu liefern.
Dazu stehen ihm die Hilfsmittel der
Statistik zur Verfügung.
Die Summenstatistik
Andere Beschreibungen der Itemcharakteristikmittels
arctan(θ-ε), tanh(θ-ε) oder die
kumul. Normalverteilung sind graphisch
nicht von der (in der Abszisse mit Faktor
1.43 gedehnten)logistischen Funktion zu
unterscheiden. Sie besitzen aber nicht die
noch zu beschreibenden Eigenschaften, die
die logistische Funktion als Theorie für die
psychologische Diagnostik so interessant
machen.
Funktionen von Daten heißen Statistiken.
Eine besonders in der Psychologie beliebte
Statistik ist die Summe richtiger Antworten.
Ihr gegenüber besitzt das Fach eine
merkwürdige Ambivalenz. Einerseits sind
Psychologen oft skeptisch, ob ein eindimensionales
Symptom sinnvoll sei. Andererseits
summieren auch sie, wie eingangs
erörtert, nicht selten bedenkenlos Unvergleichliches.
Deshalb müssen die Eigenschaften
von Statistiken, auch der Summenstatistik
analysiert werden.

Bedingte Wahrscheinlichkeit
Für jede bedingte Wahrscheinlichkeit gilt:
P ( u | s)
i,
j
P ( u , s)
i,
j
P( s)
und deshalb auch unter der zusätzlichen
Bedingung
P ( u | s, )
i,
j
P ( u , s | )
i,
j
P( s | )
Erschöpfungseigenschaft
der Statistik beschreibt faktorisieren, dann
ist bei gegebener Statistik die Auftretenswahrscheinlichkeit
der Daten ebenso durch
die Statistik allein bestimmt, wie in Abwesenheit
der Erschöpfungseigenschaft nur
durch die Daten.
Erschöpfungseigenschaft der Summenstatistik
im Rasch-Modell als Lehrsatz formuliert
Wegen der hervorragenden Bedeutung der
Erschöpfungseigenschaft für jede Skalierung
überhaupt wird sie hier noch einmal nach dem
Euklidschen Schema von Voraussetzung, Behauptung,
Beweis formuliert:
Voraussetzungen:
Dieses Attribut von Parameterschätzungen
ist definiert als
P ( u | s, ) P ( u | s )
i , j
i , j
Es verlangt, daß bei gegebener Statistik die
Daten stochastisch unabhängig von sind.
1. das Rasch-Modell
P 0 u i, j
= 1, q i
, 3 j 1 =
2. Die Summenstatistik:
n
s i
=
j
> u i,
= 1
e 0 q i K 3 j1
1 C e 0 q i K 3 j1
Faktorisierungsbedingung
Manchmal ordnet man die sich unter der
Erschöpfungseigenschaft ergebende Formel
anders:
P ( u | ) P ( s | ) P ( u | s )
i , j
i , j
und spricht von einer Faktorisierungsbedingung
der Likelihood. Dabei ist für die
Verbundwahrscheinlichkeit von uij und s
die Wahrscheinlichkeit von uij allein eingesetzt,
weil mit der Kenntnis von uij und
der Berechnungsvorschrift für die Statistik,
die Summenbildung, s gegeben ist.
Bedeutung dieser Bedingung
Läßt sich die Likelihood der Daten in einen
Faktor, der die Wahrscheinlichkeit des
Auftretens des Wertes der Statistik und
einen Faktor, der die Wahrscheinlichkeit
der Daten in alleiniger Abhängigkeit von
3. Die Erschöpfungseigenschaft:
L ( U, s, q ) = L ( U, s )
Behauptung
Satz: Die Summenstatistik im Raschmodell
besitzt die Erschöpfungseigenschaft.
Beweis
Die Likelihood-Funktion für eine Aufgabe und
eine Versuchsperson lautet:
q1 := L ( u, q, 3 ) = e 0 u i, j 0 q i K 3 j1 1
Die Likelihood für eine Person und n Aufgaben
(Das ? bedeutet ε) :
n
e 0 u i, j 0 q i K 3 j1 1
q2 := L ( U, q, ? ) = ?
j = 1
Wegen der Rechenregeln für Exponenten läßt
sich q2 schreiben als:
æ
ç
ç
è
1 C e 0 q i K 3 j1
1 C e 0 q i K 3 j1
ö
÷
ø

q3 := L ( U , q, ? ) = e æ
Summierung ist ein linearer Operator und läßt
sich deshalb in die Klammer „hineinmultiplizieren"
q4 := L ( U , q,
æ æ
ç
ç q ç
i ç
? ) = e è è
n
>
j = 1
Die Summe von Einsen und Nullen ist gleich
der Summe der vorgekommenen Einsen, also
der Summe richtig gelöster Aufgaben der
Person i :
q5 := L ( U , q, ? ) =
u i, j ö
÷
÷
ø
Man sieht, daß diese Likelihood faktorisierbar
ist in einen Ausdruck, der nur von der Statistik
aber nicht mehr von den Daten abhängt, und
einen der von den Daten aber nicht mehr von
abhängt. Die Erschöpfungseigenschaft der
Statistik ist damit bewiesen.
ç
ç
è
n ö
K > u 3 ÷
i, j j ÷
j = 1 ø
n
?
0 0 q i K 3 j1 1 C e 1
j = 1
æ
ç
ç
e è
n
> u i, j 0 q i K 3 j1
j = 1
n
q s K i i >
j = 1
ö
÷
÷
ø
n
?
0 0 q i K 3 j1 1 C e 1
j = 1
u i, j 3 j ö
÷
÷
ø
n
?
0 0 q i K 3 j1 1 C e 1
j = 1
relative Häufigkeiten von null oder eins auftreten,
für die keine logits existieren, und dann in
logits log (p/(1-p)) umgewandelt. Da logits die
Umkehrfunktion des Modells darstellen, bedeuten
die Eintragungen nun θ – ε :
0.405 -0.847 -1.73 -2.20 -3.66
1.39 0.100 -1.39 -2.51 -2.20
2.51 1.10 -0.100 -1.24 -2.94
2.94 1.95 1.24 0.405 -0.969
3.66 3.66 1.73 1.55 0.511
Wegen der fehlenden Eindeutigkeit der Skalierung
kann man nun den
Ursprung für beide willkürlich ansetzen und
die Größe der Niveaus in beiden Variablen aus
den mittleren Differenzen bestimmen.
Kleinere Stichproben
Hat man z. B. nur 15 Vpn. untersucht, dann
ergeben sich Häufigkeiten wie
diese:
1 0 0 0 0
2 2 2 0 0
2 2 1 0 0
3 3 3 0 1
3 3 3 3 2
Da die Randsummen ebenfalls die Erschöpfungseigenschaft
besitzen, kann man sie in
relative Häufigkeiten, umrechnen und auswerten:
Auswertungsbeispiel
Auf Grund der Erschöpfungseigenschaft der
Summenstatistik lassen sich beispielsweise
200 Vpn. in fünf gleichgroße Gruppen nach
der erreichten Gesamtpunktzahl zusammenfassen.
Entsprechendes geschieht für die Aufgaben
(Spalten):
24 12 6 4 1
32 21 8 3 4
37 30 19 9 2
38 35 31 24 11
39 39 34 33 25
Diese Lösungshäufigkeiten werden zunächst in
relative Häufigkeiten. Dies ist nur bei größen
Versuchspersonenzahlen möglich, da sonst
Randsummenauswertung
1
6
5
10
14
Die logits der Randsummen existieren, solange
keine Nullen oder Einsen als relative Häufigkeiten
auftreten.

-2.64
-0.405
-0.693
0.693
2.64
Sie werden als Differenzen der verschiedenen
θ zu einem mittleren ε aufgefaßt und unter
Benutzung der freien Ursprungswahl zahlenmäßig
bestimmt. Entsprechendes wiederholt
man für die Spaltensummen und die Ausprägungen
der ε.
Was bedeutet ?
Die Bedeutung von wird durch Bildung
der Umkehrfunktion der Rasch-Modells
deutlich:
Die logarithmierte Wettchance ist gleich
der Parameterdifferenz. Alle weitergehende
Bedeutung liegt in den Aufgaben selbst.
Spezifische Objektivität
Aus den Ausdrücken für die Wahrscheinlichkeiten
der Lösung einer Aufgabe durch
eine und eine andere Person läßt sich durch
Abziehen der beiden Umkehrfunktionen
voneinander der Aufgabenparameter eliminieren:
Pi,
j
log( )
1 P
i,
j
Pk,
j
log( )
1 P
k,
j
Pi,
j
log( )
1 P
i
k
j
i,
j
j
Die Differenz der logarithmierten Wettchancen
zweier Personen hängt nicht von
der betrachteten Aufgabe ab (ist für alle
Aufgaben gleich).
P
P
i , j k , j
log( ) log( )
1 P 1 P
i , j k , j
i
i
j
k
Diese Aussage setzt voraus, daß das
Rasch-Modell in gerade betrachteten Fall
empirisch gilt, weil nur dann sämtliche
aufgaben gleichartig sind. Wie die empirische
Geltung festgestellt wird, kommt später
zur Sprache.
Spezifische Objektivität
Aus den Ausdrücken für die Wahrscheinlichkeiten
der Lösung einer Aufgabe durch
eine und eine andere Person läßt sich durch
Abziehen der beiden Umkehrfunktionen
voneinander der Aufgabenparameter eliminieren:
Pi,
j
log( )
1 P
i,
j
Pk,
j
log( )
1 P
k,
j
i
k
j
j
Die Differenz der logarithmierten Wettchancen
zweier Personen hängt nicht von
der betrachteten Aufgabe ab (ist für alle
Aufgaben gleich).
P
P
i , j k , j
log( ) log( )
1 P 1 P
i , j k , j
Diese Aussage setzt voraus, daß das
Rasch-Modell in gerade betrachteten Fall
empirisch gilt, weil nur dann sämtliche
aufgaben gleichartig sind. Wie die empirische
Geltung festgestellt wird, kommt später
zur Sprache.
Hinreichende und notwendige empirische
Bedingungen
Man definiert die einer Person i äquivalente
Aufgabe j durch Gleichheit von i und
j. Eine Aufgabe j ist demnach einer Person
i äquivalent, wenn Pij = ½. Nun lassen
sich Personen bzw. Aufgaben untereinander
vergleichen. Ein praktisches Beispiel
i
k

ist etwa das Tennisspiel, bei dem der Spieler
mit einem Gegner als „Aufgabe“ konfrontiert
ist.
Aus den drei Vergleichswahrscheinlichkeiten
für drei Aufgaben (oder drei Personen),
lassen sich deren Parameter sämtlich eliminieren.
Es ergibt sich so die Multiplikationsbedingung.
Multiplikationsbedingung (Luce,1959).
P P
i , j j , k
Pik
,
log( ) log( ) log( )
1 P 1 P 1 P
oder:
i , j j , k i , k
Betrachtet man die P als Beobachtungen
von relativen Häufigkeiten (richtiger Lösungen),
dann ist die Multiplikationsbedingung
eine empirische Formulierung von
Raschs Latent Trait Theorie, weil sie parameterfrei
ist. Grundsätzlich ließe sich
diese Form zur empirischen Modellprüfung
benutzen, sofern man alle aus den
Aufgaben zu bildenden Tripel untersucht.
Praktisch ergeben sich dabei allerdings
Schwierigkeiten in der Beobachtung von
hinreichend großen absoluten Häufigkeiten,
sowie bei der Formulierung einer geeigneten
statistischen Nullhypothese. Man
benutzt deshalb später zu besprechende
andere Modelltests.
Eigenschaften von Abständen D
(x, x) = 0. (1)
(x, y) > 0 für x ¹ y. (2)
(x, y) = D (y, x). (3)
(x, y) + D (y, z) ³ D (x, z). (4)
Beispiel:
P P P
i , j j , k ik ,
1 P 1 P 1 P
i , j j , k i , k
--O---------------------------O---------------O-
x y z
Würzburg Nürnberg Regensburg
Lineare Abhängigkeit
Bei Geltung der Multiplikationsbedingung
wird die Dreiecksungleichung zur Gleichung.
Die beiden Summanden links ergeben
dann stets den rechten Term. Man sagt,
die drei Abstände sind linear abhängig.
Geometrisch wird lineare Abhängigkeit
von je drei Elementen als Eindimensionalität
gedeutet. Diese Eigenschaft der Abstände
führt dazu, daß man aus je zwei
Abstanden den dritten berechnen kann.
Aus zwei Vergleichen dreier Personen ist
das Resultat des ausstehenden dritten Vergleichs
vorherzusagen. Aus zwei Vergleichen
dreier Personen ist das Resultat des
ausstehenden dritten Vergleichs in Wahrscheinlichkeit
berechenbar
Beispiel:
Wenn Person i von Person j den Abstand
0,5 besitzt und Person j von Person k den
Abstand 1,5 , dann besitzt Person i von
Person k den Abstand 2. Wegen 2 = log
(pik/(1 - pik)) ist die Wahrscheinlichkeit
pik, daß Person i das Niveau von Person k
übertrifft gleich 0,88.
Multiplikationsbedingung als Modelltest
Man kann alle Tripel von logits daraufhin
untersuchen, ob ihre Summe Null ist. Es
ergibt sich eine Verteilung um Null. Deren
Streuung kann man beurteilen, wenn man
die gleiche Verteilung aus vorgegebenen
Skalenwerten simuliert und dann verschiedene
„Verrauschungen“ einführt und vergleicht.
Auch hier ist das logit gleich der
Differenz zweier Skalenwerte.
Beispiel
Seien drei Tennisspieler i, j, k gegeben,
deren Spielstärken i =1, j = 2 und k = 4

etragen. Dann sind die drei Differenzen ij
= 1, jk = 2 und ik = 3. Daraus lassen sich
die paarweisen Gewinnwahrscheinlichkeiten
berechnen. Die Differenzen addieren
sich zu Null. Überlagert man die Differenzen
mit einer (normalverteilten) Fehlerkomponente
, dann bilden sie eine Verteilung
um Null, deren Streubreite von der
Größe der Fehlerkomponente abhängt.
Ableitung des Rasch-Modells
Unter der Voraussetzung einer erschöpfenden
Statistik s, der Eindimensionalität und
der lokalen stochastischen Unabhängigkeit
läßt sich das Rasch-Modell ableiten. Zunächst
wird die Faktorisierungsbedingung
für eine Statistik von s = 1 formuliert.
PU ( [1, 0] |
oder
h
P( s 1 | )
PU ( [0,1] |
h
h
P( s 1 | )
h
h)
h)
Zwei Aufgaben g und f.
P ( U [1, 0] | s 1)
h
P ( U [0,1] | s 1)
Bei h = k = läßt sich wegen der lokalen
stochastischen Unabhängigkeit schreiben
P ( U [1, 0] | P (1 P )
und
h ) h , g h , f
P ( U [0,1] | P (1 P )
k ) k , f k , g
Wahrscheinlichkeit für s = 1
Weil logisch „oder“ disjunkter Ereignisse
der Addition von Wahrscheinlichkeiten
entspricht, gilt
P ( s 1 | ) P (1 P ) P (1 P )
h , g hf h , f h , g
h
Kombinieren der beiden Gleichungen
durch Division
PU ( [1, 0] | )
(1 P )
h , g h , f
P ( s 1 | ) P (1 P ) P (1 P )
P
h , g h , f h , f h , g
unabhängig von . Vereinfacht
PU ( [1, 0] | ) 1
P( s 1 | )
1
P
P
Spezifische Objektivität
(1 P )
h , f h , g
(1 P )
h , g h , f
Das Verhältnis der Wettchancen zweier
Aufgaben f,g ist für eine Person h
1
P
1
P
h , f
h , g
P
P
h , f h , g
k
f , g
unabhängig von . Aus Symmetriegründen
gilt dies auch für den Vergleich zweier
Personen mittels einer beliebigen Aufgabe.
Psychologische Bedeutung von k
Andersen hat gezeigt, daß die Interpretation
dieser Konstanten k als Verhältnis εf /
εg der betreffenden Aufgabenschwierigkeiten
die Entwicklung mit einem psychologischen
Sachsinn versieht und gleichzeitig
die Ableitung vollendet.
Multiplikationsbedingung
Die Wahl der Konstanten k = εf / εg führt
dazu, daß Sich bei einer multiplikativen
Kombination von drei Wettchanchen sämtliche
Parameter herauskürzen:
P
1
P
P
i , j ik , j , k i k j
1 P P 1 P
i , j i , k j , k j i k
Das ist die Multiplikationsbedingung von-
Luce(1959. Sie ist hinreichend und notwendig
für das Rasch-Modell. Deshalb ist
damit die Ableitung vollzogen.)
0
1

Eindimensionalität
Logarithmiert man die Multiplikationsbedingung,
dann werden aus den Quotienten
der Parameter Differenzen und die entstehenden
logarithmierten Wettschancen weisen
als „Logits“ eine lineare Abhängigkeit
auf.
Pi , j
1 P P
ik ,
j , k
log log log
1 P P 1 P
.
i , j i , k j , k
i
k
log log log 0
j i k
Beweis für n Aufgaben
Dieser Beweis einer Ableitbarkeit eines
Rasch-Tests bestehend aus zwei Aufgaben
aus der Erschöpfungseigenschaft einer
Summenstatistik von 1, der lokalen stochastischen
Unabhängigkeit und der Eindimensionalität
ergibt den Induktionsanfang
für einen allgemeinen Beweis.
Es läßt sich zeigen, daß unter Beibehaltung
der Annahmen die schrittweise Vergrößerung
der Summenstatistik von 1 auf 2, 3, ...
, n zu einem Rasch-Test von n Aufgaben
führt.
Test-Information
Die logarithmierte Likelihood-Funktion
log( L) ist für stochatisch unabhängige
Daten X und Y additiv.Wegen L( |
X,Y)=L1( | X) L2( |Y) gilt
log L( |X,Y) = log L1( | X) + log L2(
|Y).
Die Log-Likelihood-Funktion wird auch
support genannt. Ihre Ableitung nach
heißt score:
Parameter des score V
V = v( X | ) = log L( | X ) / = L´(
) / L ( ).Der Erwartungswert des score
ist gleich Null:
(V) = ([v( X | )] = 0.
j
Die Varianz des score ist die Fishersche
Information I Der Stichprobe X:
IX( ) = var (V) = { [ log ( L ( X | )/
]² }
Additivität der Information
Satz: Für unabhängige Experimente X und
Y ist Information additiv:
I X,Y ( ) = I X ( ) + I Y ( ).
Deshalb ergibt auch die Information einer
Stichprobe n-fachen Umfangs Z = ( X1,X2,
... ,Xn )die n-fache Information.
I Z ( ) = n I X ( ).
Information erschöpfender Statistik
Satz: Die Information, die durch eine erschöpfende
Statistik beigetragen wird, ist
gleich der Information der Stichprobe.
Das folgt aus der Faktorisierungsbedingung:
F ( X | ) = g( t(X), ) h( X ).
Satz: Bei der Reduktion einer Stichprobe
auf eine Statistik kann Information verlorengehen,
es sei denn die Statistik ist erschöpfend:
Ist T = t( X ), dann gilt
I T ( ) I X ( ).
Parameterschätzung
Sei U = 0,1 eine Zufallgröße, und ,
Parameter, i der Personenindex, j der Aufgabenindex,
dann ist die Wahrscheinlichkeit
exp( u ( ))
i , j i j
P ( U u | , )
i , j i j
1 exp( u ( ))
i , j i j
als Likelihood-Funktion für eine Aufgabe
und eine Person zum Rasch-Modell gegeben.

Erweiterung auf mehrere Aufgaben
Betrachtet man die Bearbeitung von n
Aufgaben einer Person, so ergibt sich:
n exp( u ( ))
i , j i j
P ( U | , , E )
i i i j j 1
1 exp( )
exp( u ( ))
n
j 1
n
j 1
i , j i j
1 exp( )
i
Maximum Likelihood Schätzung
j
Im weiteren setzt man h = exp(h) und
g= exp(g). Dabei ist h der Personen- und
g der Aufgabenindex. Dann gilt
P
h,
g
h
h
1 1
h g h g
h
mit = 1/ der Aufgabenleichtigkeit.
Neue Schreibweise der Likelihood
h,
g
g
h
h g uh , g
h g 1 uh , g
L( u | , ) ( ) (1 ( )
h,
g
1 1
L( u | , )
( )
1
h
g
h g h g
h
u h,
g
Erweiterung der Likelihood auf mehrere
Aufgaben
sh
h
g , h g 1 k k
L( u | , ,..., )
g
i 1
u h1
1
g
,...,
(1 , )
i
h
u hk
k
Ausmultiplizieren des Nenners rechts führt
zur elementarsymmetrische Funktion k-ter
Ordnung, die man mit γk abgekürzt.
Elementarsymmetrische Funktionen
sind Produktsummen aller Tupel der Parameter:
i
j
0
...
1,
1 1 2
2 1 2 1 3 k 1
3 1 2 3 1 2 4 k 2 k 1 k
k
k
g
1
g
.
... ,
k
... ,
k
... ,
Grundsätzlich gibt es zwei Möglichkeiten
eine Maximum-Likelihood Schätzung der
Parameter anzusetzen. Die erste besteht in
der Formulierung der Likelihood für die
gesamte Datenmatrix, deren Maximierung
in Abhängigkeit von den gesuchten Parametern
und Auflösung nach den gesuchten
Parametern. Dieser Zugang führt zu einfacheren
Formeln, wird aber dennoch nicht
gern begangen. Die gemeinsame Schätzung
von Person- und Aufgabenparametern
ermöglicht keine konsistenten Parameterschätzungen,
da eine Vergrößerung der
Stichprobe stets mit einer Vermehrung der
Parameteranzahl einhergeht.
Der andere Ansatz geht von der Formulierung
der bedingten Likelihood unter der
Bedingung der beobachteten Zeilen- sowie
Spaltensummen der Datenmatrix aus. Dazu
muß entsprechend dem Satz von Bayes
neben der Likelihood der Datenmatrix
auch die Likelihood der Bedingung bestimmt
werden. Der Quotient dieser beiden
Größen ist die bedingte Likelihood, die
maximiert und nach den Parametern ausgewertet
werden kann. Die Formulierung
dieses Ausdrucks ist nicht ganz einfach, da
bei festen Randsummen einer Matrix mehrere
Datenmatrizen infrage kommen, die
diese Randsummen hervorgebracht haben.
Die Bestimmung dieser Anzahl ist ein
kombinatorisches Problem, das schon
Rasch (1960) bearbeitet hat. Man kann den
kombinatorischen Koeffizienten mittels
elementarsymmetrischer Funktionen der i
bestimmen. Dieses Symbol bedeutet hier
uij ist in der gerade betrachteten Zeile der
Datenmatrix in der i-ten Spalte gleich eins.
In der sich auf diese Weise ergebenden
elementarsymmetrischen Funktion der i
ergibt sich der gesuchte kombinatorische

Wert als Koeffizient desjenigen Produkts
von Potenzen der 12 …k (k ist die Spaltenanzahl
der Datenmatrix), dessen Potenzen
bei den einzelnen i gleich den Spaltensummen
sind. Diese Koeffizient kann
rechnerisch durch Ableitung nach den i
gefunden werden. Fischer (1974) beschreibt
das Verfahren im einzelnen, erklärt
aber auch, wie es iterativ in den eigentlichen
Parameterschätzprozess eingegliedert
werden kann.
Diesem Verfahren wird, obwohl etwas
komplizierter, der Vorzug gegeben, weil
damit die Aufgabenparameter unabhängig
von den Personparametern geschätzt werden
können. Bei der Formulierung der bedingten
Likelihood fällt jeweils eine Art
der Parameter heraus.
Das iterative Verfahren wird in folgenden
Schritten vollzogen:
Likelihood einer gesamten Datenmatrix
G( , n )
n*
i
v*
n*
i
i
nv*
für 0 n n und
n
* i
K
i
* i
n
v
Die bedingte Likelihood ist dann der Quotient,
bei dem die Personenparameter ξ
herausgefallensind („Trennung der Parameter“,
„Spezifische Objektivität“):
n*
I
i
L P ( n | n ) K
* i v*
G nv
*
( , )
Maximierung der logarithmierten Likelihood
Nun wird in diesen Ausdruck für K und G
eingesetzt, logarithmiert, nach den gesuchten
ω abgeleitet, und nullgesetzt. Es ergibt
sich die (implizite) Schätzgleichung
P{ n , n | , } K
v* * i
v
v
i
n v *
i
* i
(1 )
Dabei ist K der kombinatorische Faktor,
der angibt, wie viele binäre Datenmatrizen
die eben gegebenen Ransummen erzeugt
haben können. Die Likelihood der Bedingung
ist
P{ n | , }
v*
v
v
i
i
v
v
Dabei ist
nv*
(1 )
nv*
v
nv*
n*
i
v i
v i
i
a*
i
G( , N )
v*
(1 )
v
i
K
v
K
i
i
* i
v
* i
(1 )
i
Nullsetzen führt zu der (impliziten) Lösung:
u
k ( g )
* g
r 1
n
r
g r 1 r
Dabei bedeutet der Ausdruck im Zähler
ganz rechts, daß in γr das g gleich Null
gesetzt wird, nach dem eben partiell differenziert
wird
Dies ist eine Schätzung der Aufgabenparameter
allein auf Grund der Randsummen
u*g und nr.
Mit Hilfe von auf dem Markt befindlichen
kommerziellen Computerprogrammen läßt
sich für die Aufgabenparameter iterativ
eine Lösung finden. Man setzt sie zu Anfang
alle mit gleichem Zahlenwert in die
rechte Seite der Gleichung ein, so daß sie
sich zu Eins aufsummieren. Dann errechnet
man die links in der Gleichung vorkommenden
ω. Diese benützt man dann

wieder rechts als Eingabe für den nächsten
Iterationsschritt. Sobald sich die jeweils
neuen nicht mehr wesentlich geändert
haben, beendet man das Verfahren. Nun
kann man mit den bekannte Aufgabenparametern
und dem Rasch-Modell die Personenparameter
berechen.
(wird fortgesetzt).
Literatur
Fischer, G.H.(1974), Einführung in die
Theorie psychologischer Tests. Bern, Huber.
Fischer, G.H.(1995) Derivation of the
Rasch Model, S.15 – 38 in Fischer, G. H,
& Molenaar,I, W., (Herausgeber) Rasch
Models, New York usw., Springer.
Fischer, G. H. & Mlenaar I,.V.: (1995)
Rasch Models, foundations, recent developments
and applications. New York,
Springer.
Hell, B., Trapmann, S., Weigand, S. & Schuler,
H: (2007) ,
Die Validität von Auswahlgesprächen im
Rahmen der Hochschulzulassung – eine Metaanalyse.
Psychologische Rundschau, 58, 2, 93 – 102.
Irtel, H.,(1996) Entscheidungs- und testtheoretische
Grundlagen der Psychologischen
Diagnostik, Frankfurt a. M., Lang,
.
Lindgren, B. W., (1968) Statistical Theory,
second edition. London, McMillan.