Download (PDF: 6.1 MB)

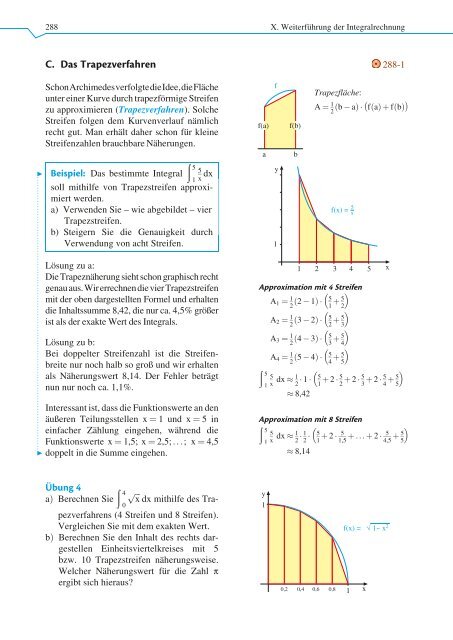
288
X. Weiterführung der Integralrechnung
C. Das Trapezverfahren 288-1
c
........................................................................................................
c
SchonArchimedesverfolgtedieIdee,dieFläche
unter einer Kurve durch trapezförmige Streifen
zu approximieren (Trapezverfahren). Solche
Streifen folgen dem Kurvenverlauf nämlich
recht gut. Man erhält daher schon für kleine
Streifenzahlen brauchbare Näherungen.
ð
5
1
5
Beispiel: Das bestimmte Integral
x dx
soll mithilfe von Trapezstreifen approximiert
werden.
a) Verwenden Sie – wie abgebildet – vier
Trapezstreifen.
b) Steigern Sie die Genauigkeit durch
Verwendung von acht Streifen.
Lösung zu a:
Die Trapeznäherung sieht schon graphisch recht
genauaus.WirerrechnendievierTrapezstreifen
mit der oben dargestellten Formel und erhalten
die Inhaltssumme 8,42, die nur ca. 4,5% größer
ist als der exakte Wert des Integrals.
Lösung zu b:
Bei doppelter Streifenzahl ist die Streifenbreite
nur noch halb so groß und wir erhalten
als Näherungswert 8,14. Der Fehler beträgt
nun nur noch ca. 1,1%.
Interessant ist, dass die Funktionswerte an den
äußeren Teilungsstellen x ¼ 1 und x ¼ 5in
einfacher Zählung eingehen, während die
Funktionswerte x ¼ 1,5; x ¼ 2,5; ...;x¼ 4,5
doppelt in die Summe eingehen.
f(a)
a
f
y
1
f(b)
b
Trapezfläche:
A ¼ 1 2 ðb aÞ fðaÞþfðbÞ
f(x) = 5 x
1 2 3 4 5 x
Approximation mit
4 Streifen
A 1 ¼ 1 2 ð2 1Þ 5
1 þ 5 2
A 2 ¼ 1 2 ð3 2Þ 5
2 þ 5 3
A 3 ¼ 1 2 ð4 3Þ 5
3 þ 5 4
A 4 ¼ 1 2 ð5 4Þ 5
4 þ 5 5
ð 5
5
1 x dx 1 2 1 5
1 þ 2 5 2 þ 2 5 3 þ 2 5 4 þ 5 5
8,42
Approximation mit 8 Streifen
ð 5
5
1 x dx 1 2 1 2 5
1 þ 2 5
1,5 þ ...þ 2 5
4,5 þ 5 5
8,14
Übung 4
aÞ Berechnen Sie
ð
4
0
pffiffi
x dx mithilfe des Trapezverfahrens
(4 Streifen und 8 Streifen).
Vergleichen Sie mit dem exakten Wert.
bÞ Berechnen Sie den Inhalt des rechts dargestellen
Einheitsviertelkreises mit 5
bzw. 10 Trapezstreifen näherungsweise.
Welcher Näherungswert für die Zahl p
ergibt sich hieraus?
y
1
0,2 0,4 0,6 0,8
f(x) = √ 1- x 2
1
x