Download (PDF: 6.1 MB)
Download (PDF: 6.1 MB) Download (PDF: 6.1 MB)
276 X. Weiterführung der Integralrechnung Übungen 4. Bestimmen Sie das Volumen des Körpers, der durch Rotation des Funktionsgraphen von f um die x-Achse über dem Intervall I entsteht. Fertigen Sie eine Skizze an. p aÞ fx ð Þ¼ ffiffi x , I¼½1;4Š bÞ fx ðÞ¼ x 4 x 2 , I¼½ 1;1Š cÞ fx ð Þ¼ 0,5x þ 2, I ¼½ 2;1Š dÞ fx ðÞ¼ ðx 2Þ 2 þ 4, I ¼½0;4Š p eÞ fx ð Þ¼ ffiffiffiffiffiffiffiffiffiffiffiffi 1 x 2 ,I¼½ 1;1Š fÞ fx ðÞ¼ xx ð 1Þ 2 , I¼½0;2Š 5. Bestimmen Sie das Volumen des Körpers, der entsteht, wenn der Graph von f zwischen den angegebenen Grenzen um die y-Achse rotiert. a) fðxÞ¼ 3x 2, y ¼ 1 bis y ¼ 4 b) fðxÞ¼ x 2 1, y¼0 bis y ¼ 3 c) fðxÞ¼ x 2 þ 1, y ¼ 1 bis y ¼ 2 d) fðxÞ¼ 1 x , y¼ 1 2 bis y ¼ 2 6. Gesucht ist das Volumen des abgebildeten Footballs, der durch Rotation einer Parabel um die x-Achse entsteht. Bestimmen Sie zunächst die Gleichung der Randparabel f. y f(x) = ax 2 + b 7. Kugelkappe Bestimmen Sie das Volumen der Kugelkappe in Abhängigkeit vom Radius r der Kugel und der Höhe h der Kugelkappe. y 7 inch x r h x 11 inch 1 4 1 inch = 2,54 cm 8. Kegelstumpf Die Formel für das Volumen des Kegelstumpfs mit den Radien R und r und der Höhe h soll hergeleitet werden. a) Das Kegelvolumen lässt sich als Rotationsvolumen darstellen. Begründen Sie dies anhand der Skizze. y R r a b x h b) Zeigen Sie, dass die als Randkurve verwendete Ursprungsgerade die Steigung m ¼ R r hat. h c) Weisen Sie nach, dass a ¼ r h R r und b ¼ R h die Integrationsgrenzen sind. R r d) Berechnen Sie das Rotationsvolumen des Kegelstumpfes. y 9. Eine Kugel mit dem Radius R ¼ 4 wird durch eine ringartige Schale eingefasst, deren Volumen gesucht ist. 5 4 1 1 x 10. fx ðÞ¼ x 2 þ 1 rotiert über [ 1;1] um die x-Achse. Ist die Maßzahl des Rotationsvolumens größer als 5? y x
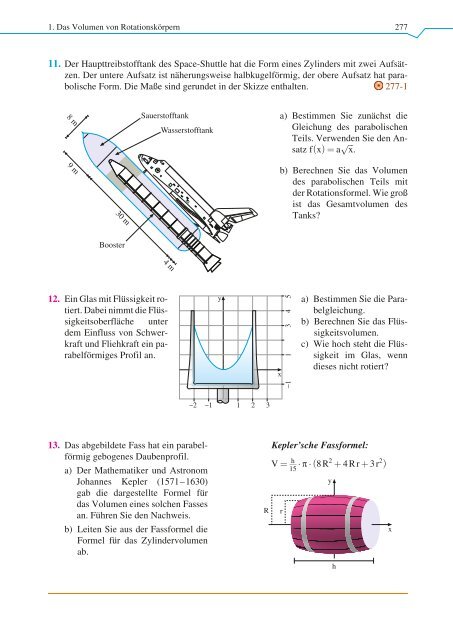
1. Das Volumen von Rotationskörpern 277 11. Der Haupttreibstofftank des Space-Shuttle hat die Form eines Zylinders mit zwei Aufsätzen. Der untere Aufsatz ist näherungsweise halbkugelförmig, der obere Aufsatz hat parabolische Form. Die Maße sind gerundet in der Skizze enthalten. 277-1 8 m Sauerstofftank Wasserstofftank a) Bestimmen Sie zunächst die Gleichung des parabolischen Teils. Verwenden p Sie den Ansatz fðxÞ¼ a ffiffi x . 9 m b) Berechnen Sie das Volumen des parabolischen Teils mit der Rotationsformel. Wie groß ist das Gesamtvolumen des Tanks? 30 m 4 m Booster 12. Ein Glas mit Flüssigkeit rotiert. Dabei nimmt die Flüssigkeitsoberfläche unter dem Einfluss von Schwerkraft und Fliehkraft ein parabelförmiges Profil an. y x 1 2 3 4 5 a) Bestimmen Sie die Parabelgleichung. b) Berechnen Sie das Flüssigkeitsvolumen. c) Wie hoch steht die Flüssigkeit im Glas, wenn dieses nicht rotiert? −1 −2 −1 1 2 3 13. Das abgebildete Fass hat ein parabelförmig gebogenes Daubenprofil. a) Der Mathematiker und Astronom Johannes Kepler (1571–1630) gab die dargestellte Formel für das Volumen eines solchen Fasses an. Führen Sie den Nachweis. b) Leiten Sie aus der Fassformel die Formel für das Zylindervolumen ab. R Kepler’sche Fassformel: V ¼ h 15 p ð 8R2 þ 4Rrþ 3r 2 Þ r y h x
- Seite 1 und 2: Bigalke / Köhler Mathematik Gymnas
- Seite 3 und 4: VII. Integrationsmethoden y Im Kapi
- Seite 5 und 6: 1. Die Produktintegration 177 c ...
- Seite 7 und 8: 1. Die Produktintegration 179 Übun
- Seite 9 und 10: 1. 2. Die Produktintegration Substi
- Seite 11 und 12: 1. 2. Die Produktintegration Substi
- Seite 13 und 14: 1. 2. Die Produktintegration Substi
- Seite 15 und 16: 1. 2. Die Produktintegration Substi
- Seite 17 und 18: VII. Integrationsmethoden 189 Über
- Seite 19 und 20: IX. Logarithmusfunktionen y In dies
- Seite 21 und 22: 1. Die Differentiation der Umkehrfu
- Seite 23 und 24: 1. 2. Die Differentiation natürlic
- Seite 25 und 26: Wie Euler Logarithmen berechnete 24
- Seite 27 und 28: 3. Die Ableitung von fðxÞ¼ln x 2
- Seite 29 und 30: 3. Die Ableitung von fðxÞ¼ln x 2
- Seite 31 und 32: 3. 4. Die Elementare Ableitung Funk
- Seite 33 und 34: 3. 4. Die Elementare Ableitung Funk
- Seite 35 und 36: 3. 5. Die Kurvendiskussionen Ableit
- Seite 37 und 38: 3. 5. Die Kurvendiskussionen Ableit
- Seite 39 und 40: 3. 5. Die Kurvendiskussionen Ableit
- Seite 41 und 42: 3. 5. Die Kurvendiskussionen Ableit
- Seite 43 und 44: 3. 5. Die Kurvendiskussionen Ableit
- Seite 45 und 46: IX. Logarithmusfunktion 269 Überbl
- Seite 47 und 48: X. Weiterführung der Integralrechn
- Seite 49 und 50: 1. Das Volumen von Rotationskörper
- Seite 51: 1. Das Volumen von Rotationskörper
- Seite 55 und 56: 2. Uneigentliche Integrale 279 Im o
- Seite 57 und 58: 2. Uneigentliche Integrale 281 Typ
- Seite 59 und 60: 2. Uneigentliche Integrale 283 Übu
- Seite 61 und 62: 3. Numerische Integrationsverfahren
- Seite 63 und 64: 3. Numerische Integrationsverfahren
- Seite 65 und 66: 3. Numerische Integrationsverfahren
- Seite 67 und 68: 3. Numerische Integrationsverfahren
- Seite 69 und 70: 3. Numerische Integrationsverfahren
- Seite 71 und 72: 3. X. Numerische Weiterführung Int
- Seite 73 und 74: XIV. Skalarprodukt und Vektorproduk
- Seite 75 und 76: 5. Das Vektorprodukt 391 c ........
- Seite 77 und 78: 5. Das Vektorprodukt 393 C. Exkurs:
- Seite 79 und 80: 5. Das Vektorprodukt 395 Übungen 1
- Seite 81 und 82: XIV. 5. DasSkalarprodukt Vektorprod
- Seite 83 und 84: XVII. Kugeln Auch Kugeln im Raum k
- Seite 85 und 86: 1. Kugelgleichungen 467 c .........
- Seite 87 und 88: 2. Kugeln, Geraden und Ebenen 469 2
- Seite 89 und 90: 2. Kugeln, Geraden und Ebenen 471 .
- Seite 91 und 92: 2. Kugeln, Geraden und Ebenen 473 .
- Seite 93 und 94: 2. Kugeln, Geraden und Ebenen 475 1
- Seite 95 und 96: 2. Kugeln, Geraden und Ebenen 477 4
- Seite 97 und 98: 2. XVII. Kugeln, Kugeln Geraden und
- Seite 99 und 100: XXII. Die Normalverteilung Die wich
- Seite 101 und 102: 1. Die Normalverteilung 601 Wird de
1. Das Volumen von Rotationskörpern 277<br />
11. Der Haupttreibstofftank des Space-Shuttle hat die Form eines Zylinders mit zwei Aufsätzen.<br />
Der untere Aufsatz ist näherungsweise halbkugelförmig, der obere Aufsatz hat parabolische<br />
Form. Die Maße sind gerundet in der Skizze enthalten. 277-1<br />
8 m<br />
Sauerstofftank<br />
Wasserstofftank<br />
a) Bestimmen Sie zunächst die<br />
Gleichung des parabolischen<br />
Teils. Verwenden<br />
p<br />
Sie den Ansatz<br />
fðxÞ¼ a<br />
ffiffi x .<br />
9 m<br />
b) Berechnen Sie das Volumen<br />
des parabolischen Teils mit<br />
der Rotationsformel. Wie groß<br />
ist das Gesamtvolumen des<br />
Tanks?<br />
30 m 4 m<br />
Booster<br />
12. Ein Glas mit Flüssigkeit rotiert.<br />
Dabei nimmt die Flüssigkeitsoberfläche<br />
unter<br />
dem Einfluss von Schwerkraft<br />
und Fliehkraft ein parabelförmiges<br />
Profil an.<br />
y<br />
x<br />
1 2 3 4 5<br />
a) Bestimmen Sie die Parabelgleichung.<br />
b) Berechnen Sie das Flüssigkeitsvolumen.<br />
c) Wie hoch steht die Flüssigkeit<br />
im Glas, wenn<br />
dieses nicht rotiert?<br />
−1<br />
−2<br />
−1 1 2 3<br />
13. Das abgebildete Fass hat ein parabelförmig<br />
gebogenes Daubenprofil.<br />
a) Der Mathematiker und Astronom<br />
Johannes Kepler (1571–1630)<br />
gab die dargestellte Formel für<br />
das Volumen eines solchen Fasses<br />
an. Führen Sie den Nachweis.<br />
b) Leiten Sie aus der Fassformel die<br />
Formel für das Zylindervolumen<br />
ab.<br />
R<br />
Kepler’sche Fassformel:<br />
V ¼ h 15 p ð 8R2 þ 4Rrþ 3r 2 Þ<br />
r<br />
y<br />
h<br />
x