Download (PDF: 6.1 MB)
Download (PDF: 6.1 MB) Download (PDF: 6.1 MB)
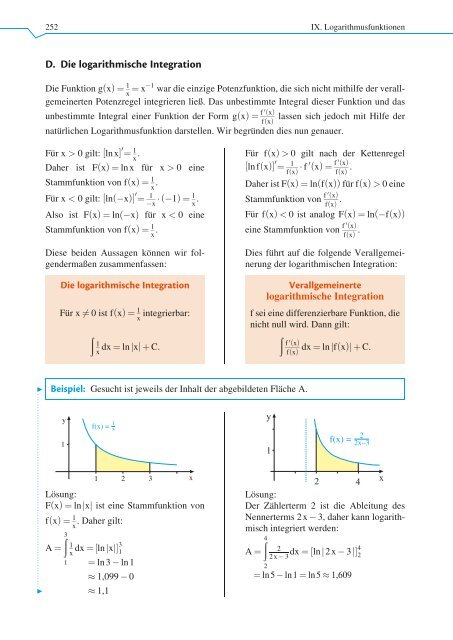
252 IX. Logarithmusfunktionen D. Die logarithmische Integration Die Funktion gx ð Þ¼ 1 x ¼ x 1 war die einzige Potenzfunktion, die sich nicht mithilfe der verallgemeinerten Potenzregel integrieren ließ. Das unbestimmte Integral dieser Funktion und das unbestimmte Integral einer Funktion der Form gx ð Þ¼ f 0 ðxÞ lassen sich jedoch mit Hilfe der fx ð Þ natürlichen Logarithmusfunktion darstellen. Wir begründen dies nun genauer. Für x > 0 gilt: ½lnxŠ 0 ¼ 1 x . Daher ist Fx ðÞ¼ lnx für x > 0 eine Stammfunktion von fx ð Þ¼ 1 x . Für x < 0 gilt: ½lnð xÞŠ 0 ¼ 1 x ð 1Þ¼ 1 x . Also ist Fx ðÞ¼ lnð xÞ für x < 0 eine Stammfunktion von fx ð Þ¼ 1 x . Diese beiden Aussagen können wir folgendermaßen zusammenfassen: Die logarithmische Integration Für x 6¼ 0 ist fx ðÞ¼ 1 x integrierbar: ð 1 x dx ¼ ln jxj þ C. Für fx ðÞ> 0 gilt nach der Kettenregel ½ln fðÞ x Š 0 ¼ 1 fx ðÞ f 0 ðÞ¼ x f 0 ðxÞ fx ð Þ . Daher ist Fx ðÞ¼ lnðfðxÞÞfür fx ðÞ> 0 eine Stammfunktion von f 0 ðxÞ fx ð Þ . Für fx ðÞ< 0 ist analog Fx ð Þ¼ lnð fx ðÞÞ eine Stammfunktion von f 0 ðxÞ fx ð Þ . Dies führt auf die folgende Verallgemeinerung der logarithmischen Integration: Verallgemeinerte logarithmische Integration f sei eine differenzierbare Funktion, die nicht null wird. Dann gilt: ð f 0 ðÞ x dx ¼ ln jf ðÞjþC. x fx ðÞ .......................................................................... c Beispiel: Gesucht ist jeweils der Inhalt der abgebildeten Fläche A. y 1 f(x) = 1 x 1 2 3 Lösung: Fx ðÞ¼ lnjxj ist eine Stammfunktion von fx ðÞ¼ 1 . Daher gilt: x ð 3 1 A ¼ x dx ¼½ln jxjŠ3 1 1 ¼ ln3 ln1 1,099 0 c 1,1 x y 1 f(x) = 2 2x−3 2 4 x Lösung: Der Zählerterm 2 ist die Ableitung des Nennerterms 2x 3, daher kann logarithmisch integriert werden: A ¼ ð 4 2 2 2x 3 dx ¼½lnj2x 3jŠ4 2 ¼ ln5 ln1 ¼ ln5 1,609
3. Die Ableitung von fðxÞ¼ln x 253 E. EXKURS: Flächeninhaltsbestimmungen mit logarithmischer Integration Mit der logarithmischen Integration lassen sich Flächenprobleme für den Fall lösen, dass die Randkurven einfache gebrochen-rationale Funktionen sind. c ............................................................................................................... Beispiel: Gegeben sind die Funktionen gx ð Þ¼ 3 2 x und hðxÞ¼ 6 ð 2xþ 2 x > 0Þ sowie die vertikale Gerade k mit der Gleichung x ¼ 4. Welchen Inhalt hat die Fläche A, die von den drei Graphen von g, h und k sowie der x-Achse umschlossen wird? Fertigen Sie zunächst eine Skizze an. Lösung: Anhand der Skizze erkennen wir, dass die Fläche A in die Teilflächen A 1 und A 2 zerlegbar ist. Die Schnittstelle der Funktionen g und h liegt bei x ¼ 1. A 1 hat den Inhalt 0,75. Zur Berechnung des Inhaltes von A 2 müssen wir im Integranden den Faktor 3 6 2xþ 2 ausklammern, um einen Bruchterm der Form f0 ðxÞ zu erhalten, den wir mittels logarithmischer Integration behandeln können. fx ð Þ A 2 hat den Inhalt 2,75. c Als Gesamtinhalt erhalten wir A 3,5. 1 y A A 1 A 2 1 Schnittstellen von g und h: 3 2 x ¼ 6 2xþ 2 6x 2 þ 6x ¼ 12 x 2 þ x 2 ¼ 0 x ¼ 1, ðx ¼ 2Þ Flächeninhalte: h i 1 3 A 1 ¼ 2 xdx¼ 3 4 x2 ¼ 0,75 0 ð 1 0 ð 4 ð 4 6 A 2 ¼ 2x þ 2 dx ¼ 3 1 1 g 4 ¼ 3 lnj2xþ 2j 1 2,75 h 2 2xþ 2 dx k x = 4 ¼ 3ln10 ð ln4 Þ Resultat: A ¼ A 1 þ A 2 3,5 x Übung 4 Berechnen Sie den Inhalt der Fläche A unter dem Graphen von f über dem Intervall I. a) fx ð Þ¼ 1 ,I¼ ½0;4Š b) fx ðÞ¼ 4x ,I¼ ½0;3Š c) fx ð Þ¼ ex ,I¼ ½ 2;2 Š x þ 3 x 2 þ 2 e x þ 1 Übung 5 Die Graphen von f und g schließen eine Fläche A ein. Bestimmen Sie deren Inhalt. a) fx ð Þ¼ 10 b) fx ðÞ¼ 1 c) fx ð Þ¼ 3x 2 10x þ 9 2x þ 1 2x gx ðÞ¼ 5xþ 10 gðxÞ¼ 5 6 x þ 8 gx ðÞ¼ 2 3 x Übung 6 Bestimmen Sie den Inhalt der Fläche A, die von den Graphen der Funktionen fx ðÞ¼ 12 gx ð Þ¼ x 2 þ 2, der vertikalen Geraden x ¼ 3 und den Koordinatenachsen umschlossen wird. 3xþ 1 und
- Seite 1 und 2: Bigalke / Köhler Mathematik Gymnas
- Seite 3 und 4: VII. Integrationsmethoden y Im Kapi
- Seite 5 und 6: 1. Die Produktintegration 177 c ...
- Seite 7 und 8: 1. Die Produktintegration 179 Übun
- Seite 9 und 10: 1. 2. Die Produktintegration Substi
- Seite 11 und 12: 1. 2. Die Produktintegration Substi
- Seite 13 und 14: 1. 2. Die Produktintegration Substi
- Seite 15 und 16: 1. 2. Die Produktintegration Substi
- Seite 17 und 18: VII. Integrationsmethoden 189 Über
- Seite 19 und 20: IX. Logarithmusfunktionen y In dies
- Seite 21 und 22: 1. Die Differentiation der Umkehrfu
- Seite 23 und 24: 1. 2. Die Differentiation natürlic
- Seite 25 und 26: Wie Euler Logarithmen berechnete 24
- Seite 27: 3. Die Ableitung von fðxÞ¼ln x 2
- Seite 31 und 32: 3. 4. Die Elementare Ableitung Funk
- Seite 33 und 34: 3. 4. Die Elementare Ableitung Funk
- Seite 35 und 36: 3. 5. Die Kurvendiskussionen Ableit
- Seite 37 und 38: 3. 5. Die Kurvendiskussionen Ableit
- Seite 39 und 40: 3. 5. Die Kurvendiskussionen Ableit
- Seite 41 und 42: 3. 5. Die Kurvendiskussionen Ableit
- Seite 43 und 44: 3. 5. Die Kurvendiskussionen Ableit
- Seite 45 und 46: IX. Logarithmusfunktion 269 Überbl
- Seite 47 und 48: X. Weiterführung der Integralrechn
- Seite 49 und 50: 1. Das Volumen von Rotationskörper
- Seite 51 und 52: 1. Das Volumen von Rotationskörper
- Seite 53 und 54: 1. Das Volumen von Rotationskörper
- Seite 55 und 56: 2. Uneigentliche Integrale 279 Im o
- Seite 57 und 58: 2. Uneigentliche Integrale 281 Typ
- Seite 59 und 60: 2. Uneigentliche Integrale 283 Übu
- Seite 61 und 62: 3. Numerische Integrationsverfahren
- Seite 63 und 64: 3. Numerische Integrationsverfahren
- Seite 65 und 66: 3. Numerische Integrationsverfahren
- Seite 67 und 68: 3. Numerische Integrationsverfahren
- Seite 69 und 70: 3. Numerische Integrationsverfahren
- Seite 71 und 72: 3. X. Numerische Weiterführung Int
- Seite 73 und 74: XIV. Skalarprodukt und Vektorproduk
- Seite 75 und 76: 5. Das Vektorprodukt 391 c ........
- Seite 77 und 78: 5. Das Vektorprodukt 393 C. Exkurs:
252<br />
IX. Logarithmusfunktionen<br />
D. Die logarithmische Integration<br />
Die Funktion gx ð Þ¼ 1 x ¼ x 1 war die einzige Potenzfunktion, die sich nicht mithilfe der verallgemeinerten<br />
Potenzregel integrieren ließ. Das unbestimmte Integral dieser Funktion und das<br />
unbestimmte Integral einer Funktion der Form gx ð Þ¼ f 0 ðxÞ<br />
lassen sich jedoch mit Hilfe der<br />
fx ð Þ<br />
natürlichen Logarithmusfunktion darstellen. Wir begründen dies nun genauer.<br />
Für x > 0 gilt: ½lnxŠ 0 ¼ 1 x .<br />
Daher ist Fx ðÞ¼ lnx für x > 0 eine<br />
Stammfunktion von fx ð Þ¼ 1 x .<br />
Für x < 0 gilt: ½lnð<br />
xÞŠ 0 ¼ 1 x ð 1Þ¼<br />
1 x .<br />
Also ist Fx ðÞ¼ lnð xÞ für x < 0 eine<br />
Stammfunktion von fx ð Þ¼ 1 x .<br />
Diese beiden Aussagen können wir folgendermaßen<br />
zusammenfassen:<br />
Die logarithmische Integration<br />
Für x 6¼ 0 ist fx ðÞ¼ 1 x integrierbar:<br />
ð<br />
1<br />
x<br />
dx ¼ ln jxj þ C.<br />
Für<br />
fx ðÞ> 0 gilt nach der Kettenregel<br />
½ln fðÞ<br />
x Š 0 ¼ 1<br />
fx ðÞ f 0 ðÞ¼ x<br />
f 0 ðxÞ<br />
fx ð Þ .<br />
Daher ist Fx ðÞ¼ lnðfðxÞÞfür fx ðÞ> 0 eine<br />
Stammfunktion von f 0 ðxÞ<br />
fx ð Þ .<br />
Für fx ðÞ< 0 ist analog Fx ð Þ¼ lnð<br />
fx ðÞÞ<br />
eine Stammfunktion von f 0 ðxÞ<br />
fx ð Þ .<br />
Dies führt auf die folgende Verallgemeinerung<br />
der logarithmischen Integration:<br />
Verallgemeinerte<br />
logarithmische Integration<br />
f sei eine differenzierbare Funktion, die<br />
nicht null wird. Dann gilt:<br />
ð<br />
f 0 ðÞ x<br />
dx ¼ ln jf ðÞjþC. x<br />
fx ðÞ<br />
..........................................................................<br />
c Beispiel: Gesucht ist jeweils der Inhalt der abgebildeten Fläche A.<br />
y<br />
1<br />
f(x) = 1 x<br />
1 2 3<br />
Lösung:<br />
Fx ðÞ¼ lnjxj ist eine Stammfunktion von<br />
fx ðÞ¼ 1 . Daher gilt:<br />
x<br />
ð 3 1<br />
A ¼<br />
x dx ¼½ln jxjŠ3 1<br />
1 ¼ ln3 ln1<br />
1,099 0<br />
c 1,1<br />
x<br />
y<br />
1<br />
f(x) = 2<br />
2x−3<br />
2 4<br />
x<br />
Lösung:<br />
Der Zählerterm 2 ist die Ableitung des<br />
Nennerterms 2x 3, daher kann logarithmisch<br />
integriert werden:<br />
A ¼<br />
ð 4 2<br />
2<br />
2x 3 dx ¼½lnj2x 3jŠ4 2<br />
¼ ln5 ln1 ¼ ln5 1,609