Download (PDF: 6.1 MB)
Download (PDF: 6.1 MB) Download (PDF: 6.1 MB)
612 XXII. Die Normalverteilung 18. Die mittlere Windgeschwindigkeit an der westlichen Ostsee beträgt 18 km/h. Die Standardabweichung beträgt 6 km/h. Zur Vorbereitung von Segelregatten werden Messungen vorgenommen bzw. Wahrscheinlichkeiten berechnet. a) Mit welcher Wahrscheinlichkeit wird bei einer Messung eine Windgeschwindigkeit über 25 km/h gemessen? b) Wie wahrscheinlich ist es, dass beim Start der Regatta der Wind mit einer Geschwindigkeit von über 15 km/h bläst? c) Es werden fünf zufällige Messungen vorgenommen. Mit welcher Wahrscheinlichkeit liegen alle Messwerte über 15 km/h? d) Mit welcher Wahrscheinlichkeit wird die Windgeschwindigkeit bei mindestens drei der zehn geplanten Regatten über 15 km/h liegen? Die Kieler Woche: Das größte Segelsport-Ereignis der Welt 19. Das Durchschnittsgewicht eines Erwachsenen beträgt 70 kg mit einer Standardabweichung von 10 kg. a) Mit welcher Wahrscheinlichkeit wiegt eine zufällig ausgewählte Person mehr als 85 kg? b) Acht Personen besteigen einen Aufzug, der eine Tragfähigkeit von 650 kg besitzt. Mit welcher Wahrscheinlichkeit wiegt keine der Personen mehr als 80 kg, so dass die Tragfähigkeit in jedem Fall gewährleistet ist? c) Für einen Test werden zwanzig Personen mit einem Gewicht zwischen 65 kg und 75 kg benötigt. Wie viele Personen muss man überprüfen, um die zwanzig Testkandidaten zu finden? 20. Die Strandstraße ist eine 30-km-Zone. Die Fahrgeschwindigkeit wurde durch Radarmessungen statistisch in der Hauptverkehrszeit zwischen 15 und 17 Uhr erfasst. Es ergab sich eine angenäherte Normalverteilung mit m ¼ 32 km/h und s ¼ 7 km/h. a) Welcher Prozentsatz der Fahrzeuge überschreitet das Geschwindigkeitslimit? b) Welcher Prozentsatz der Fahrer erhält ein Bußgeld, wenn dies ab 35 km/h verhängt wird? c) Die Geschwindigkeitsbegrenzung wird versuchsweise auf 50 km/h angehoben. Danach ergibt eine Messung, dass nur noch 30% der FahrerdasLimitüberschreiten.WelcheDurchschnittsgeschwindigkeit wird nun gefahren, wenn die Standardabweichung 10 km/h ist?
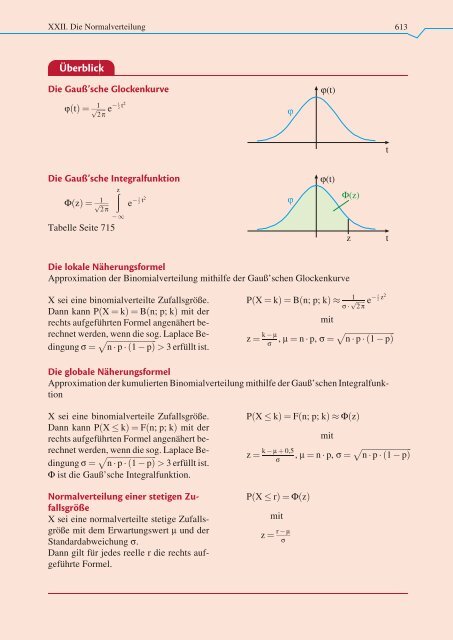
2. XXII. Anwendung Die Normalverteilung der Normalverteilung 613 Überblick Die Gaußsche Glockenkurve ϕ(t) jðtÞ¼ 1 ffiffiffiffiffiffi 2p ϕ p e 1 2 t 2 t Die Gaußsche Integralfunktion ϕ(t) ð z 1 FðzÞ¼ p 1 ffiffiffiffiffiffi 2 p e 1 2 t 2 ϕ Φ(z) Tabelle Seite 715 z t Die lokale Näherungsformel Approximation der Binomialverteilung mithilfe der Gauß’schen Glockenkurve X sei eine binomialverteilte Zufallsgröße. Dann kann PðX ¼ kÞ¼Bðn; p; kÞ mit der rechts aufgeführten Formel angenähert berechnet werden, wenn die sog. Laplace Bedingung s ¼ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi n p ð1 pÞ > 3 erfüllt p ist. PðX ¼ kÞ¼Bðn; p; kÞ 1 z ¼ k m s pffiffiffiffiffiffi e 1 2 z 2 s 2 p mit pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi , m ¼ n p, s ¼ n p ð1 pÞ Die globale Näherungsformel Approximation der kumulierten Binomialverteilung mithilfe der Gauß’schen Integralfunktion X sei eine binomialverteile Zufallsgröße. Dann kann PðX kÞ¼Fðn; p; kÞ mit der rechts aufgeführten Formel angenähert berechnet werden, wenn die sog. Laplace Bedingung s ¼ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi n p ð1 pÞ > 3 erfüllt ist. p F ist die Gauß’sche Integralfunktion. Normalverteilung einer stetigen Zufallsgröße X sei eine normalverteilte stetige Zufallsgröße mit dem Erwartungswert m und der Standardabweichung s. Dann gilt für jedes reelle r die rechts aufgeführte Formel. PðX kÞ¼Fðn; p; kÞFðzÞ z ¼ k m þ 0,5 s PðX rÞ¼FðzÞ mit z ¼ r m s mit p , m ¼ n p, s ¼ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi n p ð1 pÞ
- Seite 61 und 62: 3. Numerische Integrationsverfahren
- Seite 63 und 64: 3. Numerische Integrationsverfahren
- Seite 65 und 66: 3. Numerische Integrationsverfahren
- Seite 67 und 68: 3. Numerische Integrationsverfahren
- Seite 69 und 70: 3. Numerische Integrationsverfahren
- Seite 71 und 72: 3. X. Numerische Weiterführung Int
- Seite 73 und 74: XIV. Skalarprodukt und Vektorproduk
- Seite 75 und 76: 5. Das Vektorprodukt 391 c ........
- Seite 77 und 78: 5. Das Vektorprodukt 393 C. Exkurs:
- Seite 79 und 80: 5. Das Vektorprodukt 395 Übungen 1
- Seite 81 und 82: XIV. 5. DasSkalarprodukt Vektorprod
- Seite 83 und 84: XVII. Kugeln Auch Kugeln im Raum k
- Seite 85 und 86: 1. Kugelgleichungen 467 c .........
- Seite 87 und 88: 2. Kugeln, Geraden und Ebenen 469 2
- Seite 89 und 90: 2. Kugeln, Geraden und Ebenen 471 .
- Seite 91 und 92: 2. Kugeln, Geraden und Ebenen 473 .
- Seite 93 und 94: 2. Kugeln, Geraden und Ebenen 475 1
- Seite 95 und 96: 2. Kugeln, Geraden und Ebenen 477 4
- Seite 97 und 98: 2. XVII. Kugeln, Kugeln Geraden und
- Seite 99 und 100: XXII. Die Normalverteilung Die wich
- Seite 101 und 102: 1. Die Normalverteilung 601 Wird de
- Seite 103 und 104: 1. Die Normalverteilung 603 c .....
- Seite 105 und 106: 1. Die Normalverteilung 605 Möchte
- Seite 107 und 108: 2. Anwendung der Normalverteilung 6
- Seite 109 und 110: 2. Anwendung der Normalverteilung 6
- Seite 111: 2. Anwendung der Normalverteilung 6
- Seite 115 und 116: Tabellen zur Stochastik 715 Tabelle
2. XXII. Anwendung Die Normalverteilung<br />
der Normalverteilung 613<br />
Überblick<br />
Die Gaußsche Glockenkurve<br />
ϕ(t)<br />
jðtÞ¼<br />
1 ffiffiffiffiffiffi<br />
2p<br />
ϕ<br />
p e 1 2<br />
t 2 t<br />
Die Gaußsche Integralfunktion<br />
ϕ(t)<br />
ð z 1<br />
FðzÞ¼<br />
p<br />
1 ffiffiffiffiffiffi<br />
2 p<br />
e 1 2<br />
t 2<br />
ϕ<br />
Φ(z)<br />
Tabelle Seite 715<br />
z<br />
t<br />
Die lokale Näherungsformel<br />
Approximation der Binomialverteilung mithilfe der Gauß’schen Glockenkurve<br />
X sei eine binomialverteilte Zufallsgröße.<br />
Dann kann PðX ¼ kÞ¼Bðn; p; kÞ mit der<br />
rechts aufgeführten Formel angenähert berechnet<br />
werden, wenn die sog. Laplace Bedingung<br />
s ¼<br />
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi<br />
n p ð1 pÞ > 3 erfüllt<br />
p<br />
ist.<br />
PðX ¼ kÞ¼Bðn; p; kÞ 1<br />
z ¼ k<br />
m<br />
s<br />
pffiffiffiffiffiffi<br />
e 1 2<br />
z 2<br />
s 2 p<br />
mit<br />
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi<br />
, m ¼ n p, s ¼ n p ð1 pÞ<br />
Die globale Näherungsformel<br />
Approximation der kumulierten Binomialverteilung mithilfe der Gauß’schen Integralfunktion<br />
X sei eine binomialverteile Zufallsgröße.<br />
Dann kann PðX kÞ¼Fðn; p; kÞ mit der<br />
rechts aufgeführten Formel angenähert berechnet<br />
werden, wenn die sog. Laplace Bedingung<br />
s ¼<br />
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi<br />
n p ð1 pÞ > 3 erfüllt ist.<br />
p<br />
F ist die Gauß’sche Integralfunktion.<br />
Normalverteilung einer stetigen Zufallsgröße<br />
X sei eine normalverteilte stetige Zufallsgröße<br />
mit dem Erwartungswert m und der<br />
Standardabweichung s.<br />
Dann gilt für jedes reelle r die rechts aufgeführte<br />
Formel.<br />
PðX kÞ¼Fðn; p; kÞFðzÞ<br />
z ¼ k m þ 0,5<br />
s<br />
PðX rÞ¼FðzÞ<br />
mit<br />
z ¼ r<br />
m<br />
s<br />
mit<br />
p<br />
, m ¼ n p, s ¼ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi<br />
n p ð1 pÞ