Komplexe Form einer Fourier-Reihe - Fakultät Informatik/Mathematik

Richter, M.: Grundwissen Mathematik für Ingenieure, Ergänzungen 1
Ergänzungen zu Kapitel 9:
9.4 Fourier-Reihen
Komplexe Form einer Fourier-Reihe
Wenn man die Beziehung (2.5)
e iϕ = cos(ϕ) + sin(ϕ)i
von Seite 74 verwendet, dann lässt sich die Fourier-Reihe der periodischen Funktion
f(x) aus der Definition 9.6 (Seite 307)
s(x) = a 0
2 + ∞
∑
k=1
∫ p
( ( 2kπ
) ( 2kπ
))
a k · cos
p x + b k · sin
p x
(9.29)
mit a 0 = 2 f(x) dx , (9.30)
p 0
a k = 2 ∫ p ( 2kπ
)
f(x) · cos
p 0
p x dx, k ∈ N\{0} , (9.31)
b k = 2 ∫ p ( 2kπ
)
f(x) · sin
p 0
p x dx, k ∈ N\{0} , (9.32)
in komplexer Form darstellen. Es gilt
Definition 9.6’: Es sei y = f(x), x ∈ R, eine periodische Funktion mit der
Periodenlänge p. Die Funktionenreihe
s(x) =
mit
∞∑
k=−∞
c k = 1 p
c k · e i 2kπ
p x (9.29 ′ )
∫ p
0
2kπ
−i
f(x) · e
p x dx, k ∈ Z, (9.30 ′ )
heißt Fourier-Reihe der Funktion f(x). Die komplexen Zahlen c k
man Fourier-Koeffizienten.
Aus e iϕ = cos(ϕ) + i sin(ϕ) (Seite 74) folgt
e −iϕ = cos(−ϕ) + i sin(−ϕ) = cos(ϕ) − i sin(ϕ) ,
woraus durch Addition
e iϕ + e −iϕ = 2 cos(ϕ) =⇒ cos(ϕ) = eiϕ + e −iϕ
= cosh(iϕ)
2
nennt

Richter, M.: Grundwissen Mathematik für Ingenieure, Ergänzungen 2
und durch Subtraktion
e iϕ − e −iϕ = 2i sin(ϕ) =⇒
sin(ϕ) = eiϕ − e −iϕ
2i
= −i sinh(iϕ)
folgen. Mit den gerahmten Formeln lassen sich die folgenden Beziehungen zwischen
den Fourier-Koeffizienten überprüfen.
Satz: Für die Fourier-Koeffizienten gilt für jedes k ∈ N
a k − ib k = 2 · c k und a k + ib k = 2 · c −k bzw.
a k = c k + c −k und b k = i(c k − c −k ),
wobei b 0 = 0 zu setzen ist. Weiterhin gilt
s n (x) = a 0
2 + n∑
k=1
( ( 2kπ
) ( 2kπ
))
a k·cos
p x +b k·sin
p x =
n∑
k=−n
c k·e i 2kπ
p x , x ∈ R .
Beweis:
b k = 2 p
∫ p
0
( 2kπ
)
f(x) · sin
p x dx = 2 p
= 1 i (c −k − c k ) = i(c k − c −k )
∫ p
0
f(x) · 1
2i
(e i 2kπ
p x − e
2kπ
−i p
x)) dx
Analog zeigt man die anderen Beziehungen.
◭
Die komplexe Form der Fourier-Reihe (9.29’) stimmt mit (9.29) überein. Für die
komplexe Form der Fourier-Reihe gelten ebenfalls die Sätze 9.8 bis 9.10 (Seiten 309
ff.).
Beispiel: Gesucht ist die Fourier-Reihe der Funktion
f(x) = e −x für 0 ≤ x < 2, f(x) = f(x + 2) , x ∈ R.
Lösung: Aus
c k = 1 2
∫ 2
0
e −x · e −ikπx dx = 1 2
∫ 2
0
e −x(1+ikπ) 1 (
dx = −
e −2(1+ikπ) − 1 )
2(1 + ikπ)
= 1 − e−2
2(1 + ikπ) = (1 − ikπ) (1 − e−2 )
, k ∈ Z, c
2(1 + k 2 π 2 0 = 1 − e−2
)
2

Richter, M.: Grundwissen Mathematik für Ingenieure, Ergänzungen 3
erhält man für k ∈ N\{0} c k · e ikπx + c −k · e −ikπx =
= 1 − (
)
e−2
(cos(kπx) + i sin(kπx)) (1−ikπ)+(cos(kπx) − i sin(kπx)) (1+ikπ)
2(1 + k 2 π 2 )
= 1 − e−2
(cos(kπx) + kπ sin(kπx)) .
1 + k 2 π2 Damit ergibt sich
s n (x) =
n∑
k=−n
c k · e i 2kπ
p x = (1 − e−2 )
+
2
Aus dem Satz 9.8 (Seite 309) folgt dann
n∑
k=1
1 − e −2
(cos(kπx) + kπ sin(kπx)) .
1 + k 2 π2 f(x) = 1 − e−2
2
+
∞∑
k=1
1 − e −2
(cos(kπx) + kπ sin(kπx)) , x ≠ 2j, (j ∈ Z). ⊳
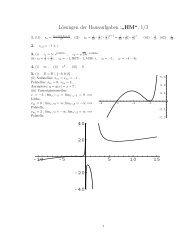
1 + k 2 π2 In der folgenden Abbildung sind die Funktionen s 5 (x) und s 15 (x) graphisch dargestellt.
An den Sprungstellen der Funktion f(x) ist das Gibbs-Phänomen zu erkennen.
y
y
1.0
1.0
0.5
0.5
4 2 2 4
x
4 2 2 4
x
s 5 (x)
s 15 (x)