blatt wiederholung 02.pdf - am Institut für Theoretische Informatik ...

Karlsruher Institut für Technologie
Institut für Theoretische Informatik
Prof. Dr. Peter Sanders
T. Bingmann, C. Schulz
2. Wiederholungsblatt zu Algorithmen I im SS 2013
Aufgabe 1
(Bellman-Ford)
http://algo2.iti.kit.edu/AlgorithmenI2013.php
{sanders,bingmann,christian.schulz}@kit.edu
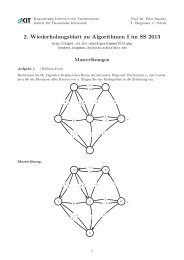
Bestimmen Sie für folgenden Graphen den Baum der kürzesten Wege mit Startknoten s, und bestimmen
Sie die Distanzen aller Knoten von s. Tragen Sie das Endergebnis in die Zeichnung ein.
−1
4
−2 3
3 −2
−2 6
6
5
−1
s
7
−1 4
1
Aufgabe 2
(Schnelles Potenzieren)
Gegeben ist der Algorithmus power(a : R; n 0 : N) aus der Vorlesung (siehe Folie 51 der Vorlesungsfolien).
Führen Sie den Algorithmus für a = 2, n 0 = 15 aus und geben Sie die Belegung der Variablen
p, r, n zu Beginn des Programms und jeweils am Ende der Whileschleife an. Nutzen Sie dafür die
folgende Tabelle!
Aufgabe 3
(Anwendungsproblem)
Durchlauf n r p
Start
1
2
3
4
5
6
7
Ein Staat möchte seine Internet-Infrastruktur erneuern. Es gibt n Städte die alle angebunden werden
sollen, wobei indirekte Verbindungen ausreichen. Eine symmetrische Matrix C = ((c ij )) ∈ R n×n
>0 informiert
darüber, wieviel Einheiten der einheimischen Währung es jeweils kosten würde, eine Leitung
zwischen je zwei Städten zu bauen.
1

a) Entwickeln Sie einen Algorithmus, der eine kostenminimale Netzinfrastruktur berechnet, die alle
n Städte direkt oder indirekt anbindet. Ihr Algorithmus darf höchsten O ( n 2 log n ) Zeit brauchen.
b) Begründen Sie kurz, warum Ihr Algorithmus das gewünschte Laufzeitverhalten aufweist.
Aufgabe 4
(Minimale Spannbäume)
a) Sei G = (V, E) ein zusammenhängender ungerichteter gewichteter Graph und T ein MST in G.
Für V ′ ⊆ V sei G ′ der von V ′ induzierte Teilgraph von G und T ′ der von V ′ induzierte Teilgraph
von T . Zeigen Sie: Wenn T ′ zusammenhängend ist, dann ist T ′ ein MST in G ′ .
b) Sei G = (V, E) ein zusammenhängender ungerichteter gewichteter Graph mit Gewichtsfunktion
c : E → R >0 . Sei T ein MST in G bzgl. der Gewichtsfunktion c.
Sei e 0 eine Kante in T und q 0 ∈ R mit c(e 0 ) ≥ q 0 ≥ 0. Wir definieren nun eine weitere Gewichtsfunktion
c 0 : E → R >0 mit c 0 (e) := c(e) für e ≠ e 0 und mit c 0 (e 0 ) := c(e 0 ) − q 0 .
Zeigen Sie: T ist auch bzgl. der Gewichtsfunktion c 0 ein MST in G.
Aufgabe 5 (MST )
Gegeben sei ein ungerichteter, zusammenhängender Graph ohne Mehrfachkanten und Schleifen. Die
Kanten seien gewichtet und o. B. d. A. nach Gewicht sortiert: w(e 1 ) ≤ w(e 2 ) ≤ . . . ≤ w(e m ). Zeigen
Sie, dass e 2 in diesem Fall immer Teil eines minimalen Spannbaums sein kann.
Aufgabe 6
(Durchmesser eines Graphen)
Skizzieren Sie einen Algorithmus, der den Durchmesser eines ungerichteten, zusammenhängenden Graphen
G = (V, E) berechnet und dabei höchstens O(nm) Zeit benötigt (n := |V |, m := |E|). Sie können
dazu einen bekannten Algorithmus modifizieren und verwenden. Begründen Sie, warum Ihr Algorithmus
das gewünschte Laufzeitverhalten hat.
Anmerkung: Der Durchmesser D eines Graphen G ist der maximale Abstand zwischen zwei Knoten
in G. Der Abstand zweier Knoten sei dabei die minimale Kantenanzahl eines Pfades zwischen diesen
Knoten in G.
Mathematisch: D := max u,v∈V min P ∈P(u,v) |P |, wobei P(u, v) die Menge aller Pfade zwischen u und
v ist, und |P | die Anzahl der Kanten in Pfad P .
Aufgabe 7
(Hashing)
Gegeben sei eine leere Hash-Tabelle mit linearem Suchen ( ”
open hashing with linear probing“). Als
Hashfunktion werde h(x) := x mod 10 verwendet.
a) Nun werde die Operationsfolge
insert(13), insert(16), insert(4), insert(14), insert(3)
ausgeführt. In welchen Zustand befindet sich die Hashtabelle nach der Ausführung? Tragen Sie
die Lösung in die folgende Tabelle ein:
2

0
1
2
3
4
5
6
7
8
9
b) Gegeben sei nun eine weitere Hash-Tabelle mit linearem Suchen ( ”
open hashing with linear
probing“). Die Operation remove sei dabei so implementiert, dass keine Löschmarkierungen
gesetzt werden (verwenden Sie den Algorithmus aus der Vorlesung). Als Hashfunktion werde
wieder h(x) := x mod 10 verwendet.
Die Hashtabelle befinde sich in dem wie folgt skizzierten Zustand:
0
1 21
2 1
3 12
4 14
5 2
6 13
7
8
9
Nun werde die Operation remove(12) ausgeführt. In welchen Zustand befindet sich die Hashtabelle
nach der Ausführung? Tragen Sie die Lösung in die folgende Tabelle ein:
Aufgabe 8
(Prioritätswarteschlangen)
0
1
2
3
4
5
6
7
8
9
a) Beschreiben Sie, wie man eine adressierbare Prioritätswarteschlange mittels einer doppelt verketteten
Liste implementiert. Ein Listenglied repräsentiere dabei ein Element in der Schlange,
ein Handle sei ein Handle eines Listenglieds. Es gelte die Invariante, dass die Liste vor und nach
jeder Operation sortiert ist. Skizzieren Sie alle Operationen der Schnittstelle und geben Sie die
asymptotischen Laufzeiten an.
b) Beschreiben Sie, wie man eine adressierbare Prioritätswarteschlange mittels einer sortierten Folge
(z. B. (a, b)-Baum) implementiert. Skizzieren Sie alle Operationen der Schnittstelle und geben
Sie die asymptotischen Laufzeiten an.
3

Aufgabe 9
(O-Notation)
a) Zeigen Sie: g(n) = O(f(n)) =⇒ O(f(n) + g(n)) = O(f(n)).
b) Zeigen Sie: O(f(n)) · O(g(n)) = O(f(n) · g(n)).
c) Für o(f(n)) wird auch die folgende, alternative Definition verwendet:
g(n) = o(f(n)) :⇐⇒ lim
n→∞ |g(n)/f(n)| = 0 .
Es soll nun bewiesen werden, dass beide Definitionen äquivalent sind für g : N ≥0 → R ≥0 und
f : N ≥0 → R >0 . Zeigen Sie also:
g(n)
lim
n→∞ f(n) = 0 ⇐⇒ ∀c ∈ R >0 : ∃n 0 ∈ N >0 : ∀n ≥ n 0 : g(n) ≤ cf(n)
Aufgabe 10
(Geldwechselproblem und dynamisches Programmieren)
Angenommen, Sie haben die Aufgabe, eine Wechselgeldrückgabe für Getränkeautomaten zu programmieren.
Ziel ist es dabei, immer die optimale (d. h. kleinstmögliche) Anzahl von Münzen zurückzugeben.
Für viele Münzwertsysteme (z. B. auch für den Euro) wird diese Aufgabe durch das Greedy-
Verfahren in Abbildung 1 optimal gelöst.
a) Im Fall des Euro ist die Menge der Münzwerte M = {1, 2, 5, 10, 20, 50, 100, 200} (alle Werte in
Cent). Zeigen Sie: Der Greedy-Algorithmus aus Abbildung 1 liefert nicht immer ein optimales
Ergebnis, wenn eine zusätzliche Münze im Wert von 4 Cent eingeführt wird.
Nun soll mit Hilfe von dynamischem Programmieren eine Algorithmus entwickelt werden, der für
jedes beliebige Münzsystem M mit 1 ∈ M stets eine optimale Lösung liefert (wäre 1 ∉ M, so könnten
manche Beträge nicht dargestellt werden).
b) Identifizieren Sie die optimalen Teillösungen einer optimalen Lösung. Die Optimalität dieser
Teillösungen muss dabei bewiesen werden. Was sind die trivialen Teilprobleme und deren trivialoptimale
Lösungen?
c) Geben Sie die optimale Lösung als Rekurrenz an.
d) Geben Sie den fertigen Algorithmus in Pseudo-Code an.
1: procedure Geldrueckgabe(rueckbetrag : N 0 , M : Set of N)
2: rest := rueckbetrag : N 0
3: while rest > 0 do
4: wähle m ∈ M sodass m maximal ist mit m ≤ rest
5: print Gib eine Münze im Wert von m zurück.
6: rest := rest − m
7: end while
Abbildung 1: Ein Greedy-Verfahren zur Bestimmung der verwendeten Münzen bei der Geldrückgabe.
Alle Werte sind natürliche Zahlen und werden z. B. in Cent angegeben. Die Menge M umfasst die
möglichen Münzwerte.
Aufgabe 11
(Listen)
In unserer einfachen Listen-Datenstruktur ist die Bestimmung der Listenlänge in konstanter Zeit nicht
möglich. Das kann durch die Einführung einer Objektvariable size behoben werden, die aktualisiert
wird, sobald sich die Anzahl der Elemente verändert. Operationen, die mehrere Listen betreffen,
müssen nun über diese Listen Bescheid wissen, obwohl Low-Level-Funktionen wie splice nur Handles
auf die betreffenden Elemente benötigen. Der Code, um ein Element a aus Liste L in Liste L ′ nach a ′
zu verschieben, wäre beispielsweise:
4

1: procedure moveAfter(a, a ′ : Handle; L, L ′ : List)
2: splice(a, a, a ′ )
3: L.size – –
4: L ′ .size++
Modifizieren Sie die Operationen remove, insertAfter und concat so, dass size korrekt aktualisiert
wird.
Aufgabe 12
(Branch-and-Bound)
Implementieren Sie einen Branch-and-Bound Algorithmus aus der Vorlesung (z.B. in Java oder C++)
und/oder implementieren Sie einen Algorithmus der alle Permtationen der Zahlen {1, . . . , n} ausgibt.
(ohne Lösung)
T U T O R E N
O-Phase 2013
G E S U C H T
!!! Werde selbst O-Phasen-Tutor !!!
Seminar vom 30. September bis 2. Oktober, Tutorentag am 12. Oktober,
O-Phase vom 14. bis 19. Oktober
Weitere Infos über die Fachschaft Mathe/Info oder unter https://www.o-phase.com/o13/tutor
Ausgabe: Mittwoch, 10.7.2013
Abgabe keine
5