Stufenfasern (STU) - TU Berlin

Einführung in die optische Nachrichtentechnik
STU/1
Stufenfasern (STU)
In diesem Kapitel wird die Wellenausbreitung in Stufenfasern behandelt. Es wird die Feldberechnung
in der Stufenfaser und die chromatische Dispersion erläutert.
Die einfachste Form eines Lichtwellenleiters besteht aus einem lichtführenden Faserkern mit der Brechzahl
n 1 und einem Fasermantel mit der Brechzahl n 2 < n 1 , wobei der Unterschied im Prozentbereich
oder sogar darunter liegt. Der Faserkerndurchmesser liegt typischerweise in der Gröÿenordnung
2a 10 100µm und der Durchmesser von Kern und Mantel bei D 125µm.
Abbildung 1: Schematische Darstellung einer Stufenfaser
Die Stufenfaser weist folgendes Brechzahlprol auf
n(r) =
⎧
⎪⎨ n 1
⎪⎩
für r a
n 2 für a < r D 2
1 sei nun der Winkel der eingekoppelten Welle zur Faserachse und 1 der Winkel, unter dem die Welle
aus dem freien Raum (n 0 = 1) in die Faser eingekoppelt wird. Die Welle wird dann im Kern geführt,
wenn 1 < 1g ist. Es gilt
Mit dem Brechungsgesetz von Snellius folgt
sin( 1g ) = √ 1 cos 2 ( 1g ) = 1 n 1
√
n 2 1 n 2 2 (2)
sin( 1g ) = n 1 sin( 1g ) = √ n 2 1 n 2 2 = A N (3)
A N wird als numerische Apertur bezeichnet und gibt den maximalen Winkel 1 an, für den die Welle
nur im Kern geführt wird. Ein typischer Wert ist A N = 0; 2, was auf einen maximalen Einfallswinkel
1g = 11; 5 führt.
(1)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/2
1 Feldberechnung in der Stufenfaser
Da die Strahlenbetrachtung die Wellenausbreitung nur für ! 0 ausreichend beschreibt, stellt sich die
Frage nach der Berechnung des Feldes in der Stufenfaser. Dazu werden die sogenannten Eigenwellen
bestimmt, die dadurch gegeben sind, dass sich eine bestimmte transversale Feldverteilung ~E(x; y)
unverändert in z-Richtung mit der Ausbreitungskonstanten ausbreitet. Die Brechzahl sei unabhängig
von z. Der Feldansatz ist dann
~E(x; y; z) = ~E(x; y) exp( j z) (4)
Zunächst soll die Gröÿenordnung von abgeschätzt werden. Aus der Strahlenbetrachtung in Abb. 1
folgt
= k 0 n 1 cos( 1 ) (5)
Für die geführte Welle ist 0 < 1 < 1g , daher ist
k 0 n 2 < < k 0 n 1 (6)
Für die kartesischen Feldkomponenten E x und E y gilt die Wellengleichung sowohl im Kern als auch
im Mantel.
4E x;y + k 2 0n 2 i E x;y = 0 (7)
mit i = 1; 2. Es folgt aus Gl. (4)
@ 2 E x;y
@z 2 = 2 E x;y (8)
und damit erhält man aus Gl. (7) die Wellengleichung
4 t E x;y + ( k 2 0n 2 i 2) E x;y = 0 (9)
mit dem transversalen Laplace-Operator 4 t = @x @2 + 2 @y @2 .
Im folgenden setzen wir einen schwach führenden Wellenleiter 2 mit
n 1 n 2
n 1
1 (10)
voraus, so dass gilt:
und damit
Daraus folgt
jk 2 0n 2 i 2 j 2 mit = k 0 n ef f und n 2 < n ef f < n 1 (11)
∣ ∣∣∣∣
@
j4 t j 2 (12)
∣
∣ ∣∣∣∣ @x ∣ ; @
@y
∣ (13)
Die Felder der ausbreitungsfähigen Wellen ergeben sich aus Gl. (7) unter Beachtung der Randbedingungen.
Die Feldkomponenten E z , H z und E ' , H ' sind stetig für r = a, wobei a der Kernradius
ist (Abb. 2).
∣
TU Berlin Prof. Dr.-Ing. K. Petermann

O
H
N
Einführung in die optische Nachrichtentechnik
STU/3
1.1 Feldkomponenten der Eigenwellen einer schwach führenden Stufenfaser
. = I A H
= J A
=
=
. = I A H
A H
-
0
-
0
=
=
Abbildung 2: Randbedingungen der Stufenfaser
Nehmen wir an, Gl. (9) sei für E x und E y gelöst. Es stellt sich dann die Frage nach der Gröÿe der
anderen Feldkomponenten. Aus der Maxwell'schen Gleichung r ~E = j! ~H folgt
H z =
(
1 @Ey
j! 0 @x
Aus der Maxwell'schen Gleichung r ~H = j!" 0 n 2 i
1
E x =
j!" 0 ni
2
E y =
1
j!" 0 n 2 i
@E x
@y
)
~E ergibt sich für E x und E y :
( )
@Hz
@y + jH y
(
@Hz
@x
jH x
)
Damit lassen sich ganz allgemein aus bekanntem E x , E y und H z aus Gl. (14) H x und H y bestimmen.
Wird nun eine schwach führende Faser angenommen (siehe Gl. (13)), lassen sich @H z =@y und
@H z =@x in Gl. (15) und Gl. (16) vernachlässigen und man kann H x und H y ausdrücken als
Für E z ergibt sich
E z =
1
j!" 0 n 2 i
(
@Hy
@x
(14)
(15)
(16)
H x !" 0n 2 i
E y (17)
H y !" 0n 2 i
E x (18)
)
@H x
@y
1
(
@Ex
j @x
Damit ist gezeigt, dass sich alle sechs Feldkomponenten aus der Kenntnis von E x und E y ableiten
lassen. Bei schwach führender Faser lässt sich dabei n i näherungsweise durch n 1 ersetzen.
@E y
@y
)
(19)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/4
1.2 Stetigkeit der tangentialen Feldkomponenten
Die tangentialen Feldkomponenten der Faser E ' , H ' , E z und H z müssen bei r = a stetig ineinander
übergehen. Für E ' und H ' gilt
E ' = E y cos(') E x sin(') (20)
H ' = H y cos(') H x sin(') (21)
Aus den Gl. (17), Gl. (18), Gl. (20) und Gl. (21) folgt mit n i n 1 , dass E x und E y stetig sein
müssen (bei r = a), wenn E ' und H ' stetig sein sollen. Da diese Stetigkeit für alle ' gelten soll,
müssen auch @E x
@' und @E y
@' für r = a stetig sein.
Wie schon oben in Gl. (14) und Gl. (19) gezeigt, lassen sich E z und H z aus E x und E y bestimmen,
wobei dort E x und E y nach x bzw. y abgeleitet werden. Die Ableitungen @x @ und @y @ lauten in
Zylinderkoordinaten
Eingesetzt in Gl. (14) und Gl. (19) folgt
E z = 1
j
H z =
(
cos(') @E x
@r
(
1
cos(') @E y
j! 0 @r
@
@x = cos(') @ 1
@r r sin(') @
@'
@
@y = sin(') @ @r + 1 r cos(') @
@'
1
r sin(')@E x
@' + sin(')@E y
@r
1
r sin(')@E y
@'
sin(') @E x
@r
+ 1 )
r cos(')@E y
@'
)
1
r cos(')@E x
@'
Da @E x
@' und @E y
@' für r = a aufgrund der Stetigkeit von E ' und H ' stetig sein müssen, folgt aus Gl.
(24) und Gl. (25), dass zusätzlich @E x
@r und @E y
@r für r = a stetig sein müssen.
Die Bedingung der Stetigkeit von E ' , H ' , E z und H z lässt sich damit durch die Forderung nach
@E
Stetigkeit von E x , E y , x
@r und @E y
@r ersetzen.
1.3 Linear polarisierte LP-Wellen
Da E x und E y bei schwach führenden Fasern durch die Wellengleichung (9) und durch die Randbedingungen
für r = a nicht miteinander verkoppelt sind, lassen sich Eigenwellen nden, bei denen
beispielsweise E y = 0 gesetzt ist. Diese Eigenwellen werden als linear polarisierte LP-Wellen bezeichnet
mit z.B.
E x = (r; ') exp( jz) (26)
und
(r; ') =
⎧
⎨
⎩
für r a
1(r; ')
2(r; ') für r > a :
(22)
(23)
(24)
(25)
(27)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/5
Aus der Wellengleichung (9) wird damit die skalare Wellengleichung
4 t i + ( k 2 0n 2 i 2) i = 0 (28)
mit i = 1; 2 und den Randbedingungen
@ 1
1j r=a = 2 j r=a (29)
j r=a = @ 2
j r=a : (30)
@r @r
Zunächst werden folgende Normierungen eingeführt:
Faserparameter: V = k 0 a √ n 2 1 n 2 2 = k 0 aA N (31)
2
k
n
Normierte Ausbreitungskonstante: 2 ( ) k0
0
B =
2 n 2 ( )
n1 2 n2
=
k0
+ n 2 k 0
n 2
p (32)
(n 1 n 2 )(n 1 + n 2 ) n 1 n 2
Kernparameter: u = V 1 B = a √
p k0n 2 1 2 2 (33)
Mantelparameter: v = V B = a √ 2 k0n 2 2 (34)
Setzt man diese Normierungen in Gl. (28) ein, so erhält man
Lösungen dieser Dierentialgleichungen sind
a 2 4 t 1 + u 2 1 = 0 für r a (35)
a 2 4 t 2 v 2 2 = 0 für r a (36)
1(r; ') = A 1 J l
(
r u a
2(r; ') = A 2 K l
(
r v a
) { }
cos(l ')
sin(l ')
) { }
cos(l ')
sin(l ')
Dabei ist J l eine Besselfunktion und K l eine modizierte Hankelfunktion ganzzahliger Ordnung. Für
niedrige Ordnungen sind sie in Abb. 3 und 4 dargestellt. Ihre Ableitungen nach dem Argument lauten
dJ l (x)
dx
dK l (x)
dx
Damit folgt aus Gl. (29) und Gl. (30)
= J 0 l (x) = J l+1 (x) + l x J l(x) = J l 1 (x)
= K 0 l(x) = K l+1 (x) + l x K l(x) = K l 1 (x)
(37)
(38)
l
x J l(x) (39)
l
x K l(x) (40)
A 1 J l (u) = A 2 K l (v) (41)
A 1
u
a J0 l (u) = A 2
v
a K0 l(v) (42)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/6
Abbildung 3: Besselfunktionen ganzzahliger Ordnung
Abbildung 4: Modizierte Bessel- und Hankelfunktionen 0. und 1. Ordnung
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/7
Dividiert man nun beide Gleichungen durcheinander, so erhält man die charakteristische Gleichung zur
Bestimmung der Ausbreitungskonstanten (u und v enthalten nur als Unbekannte).
Mit Gl. (39) und Gl. (40) folgt
u J0 l (u)
J l (u)
u J l+1 (u)
J l (u)
= v K 0 l (v)
K l (v)
+ v K l+1(v)
K l (v)
(43)
= 0 (44)
mit V 2 = u 2 + v 2 .
Für vorgegebenes V und vorgegebene Umfangsordnung l kann die Ausbreitungskonstante aus Gl.
(44) numerisch bestimmt werden. Die Gleichung hat im allgemeinen mehrere Lösungen, die mit p =
1; 2; 3::: nummeriert werden. p bezeichnet dabei die Anzahl der Feldextrema in radialer Richtung. Daher
wird die Bezeichnung LP lp -Welle mit der Umfangsordnung l und der radialen Ordnung p gewählt.
(Feldverteilungen einiger LP l p-Wellen sind in Abb. 5 dargestellt.)
Mit vorgegebener Dimensionierung (a; ; n 1 ; n 2 ) folgt V , damit kann aus Gl. (44) u und v bestimmt
werden. Daraus ergibt sich mit Gl. (33) und Gl. (34) und mit Gl. (37) und Gl. (38) auch die
Feldverteilung (r; '). Die Lösung von Gl. (44) ist in Abb. 6 dargestellt. Sie zeigt die normierte
Phasenkonstante B ( vergl. Gl. (32)) als Funktion von V .
1.4 Einwelligkeitsbereich
In Abb. 6 kann man sehen, dass nur die LP 01 -Welle für beliebig kleine V ( V Frequenz) ausbreitungsfähig
ist. Diese Welle wird auch als Grundwelle (fundamental mode) bezeichnet.
Die charakteristische Gleichung der LP 01 -Welle lautet gemäÿ Gl. (44):
u J 1 (u)
J 0 (u)
v K 1 (v)
K 0 (v)
= 0 (45)
Diese Gleichung führt zu Lösungen auch für beliebig kleine V . Dabei breitet sich die Welle dann
allerdings im wesentlichen im Fasermantel aus, da B 0, woraus folgt, dass k 0 n 2 . Sie ist damit
schlecht geführt. Für eine bessere Führung sollte V schon etwas gröÿer sein, z.B. V > 1; 5.
Für einen Faserparameter 1; 5 < V < 2; 5 wird Gl. (45) näherungsweise gelöst durch:
v = 1; 1428V 0; 996 (46)
Im Einwelligkeitsbereich darf die LP 11 -Welle (vergl. Abb. 6) nicht ausbreitungsfähig sein. Die charakteristische
Gleichung der LP 11 -Welle folgt aus Gl. (43) mit l = 1 zu:
u J 0 (u)
J 1 (u)
+ v K 0(v)
K 1 (v)
= 0 (47)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/8
Abbildung 5: Feldverteilungen einiger LP-Moden. Von oben: LP 01 , LP 11 , LP 25 und LP 73 (aus: Voges/Petermann,
Handbuch Optische Kommunikationstechnik)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/9
Abbildung 6: Normierte Phasenkonstante B von LP lp -Wellen in schwach führenden Stufenfasern (aus:
Voges/Petermann, Handbuch Optische Kommunikationstechnik)
Die Grenze der Ausbreitungsfähigkeit der LP 11 -Welle ist erreicht, wenn für den Mantelparameter gilt:
v = 0 Mit dieser Bedingung kann aus Gl. (47) der Kernparameter u c bestimmt werden.
u c J 0 (u c )
J 1 (u c )
= 0 ) J 0 (u c ) = 0 (48)
Der Kernparameter u c entspricht also der ersten Nullstelle der Besselfunktion J 0 (x). Daraus ergibt
sich ein Kernparameter von u c (LP 11 ) = 2; 405. Mit V = p u 2 + v 2 folgt daraus V c = 2; 405. Das
bedeutet, dass für einen Faserparameter V < 2; 405 eine einmodige Faser vorliegt ( allerdings ist die
dann verbleibende LP 01 -Welle noch in 2 Polarisationen ( E x und E y ) ausbreitungsfähig). Normalerweise
wird ein Faserparameter V > 1; 5 gewählt, da die Welle sonst zu schwach auf den Faserkern
konzentriert ist.
Als Beispiel sei eine Faser folgendermaÿen dimensioniert:
Faserdurchmesser: 2a = 8µm
Relative Brechzahldierenz: = n 1 n 2
= 310
n 3
1
Numerische Apertur: A N = 0; 116
Faserparameter:
V = 2; 9 µm
Mit dieser Faser wäre ein einwelliger Betrieb also für Wellenlängen 1; 2µm < < 1; 9µm möglich.
(r) des Grundmodes wird häug durch eine Gauÿverteilung angenähert:
( )
r 2
(r) = A 0 exp
w 2 : (49)
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/10
w entspricht hierbei dem Fleckradius.
Bei einer Stufenfaser mit V > 1; 2 ist w a 0; 65 + 1;619
V
+ 2;879
3=2 V . Mit steigendem V nimmt also der
Fleckradius ab. Dies entspricht einer zunehmenden Konzentration 6
des Feldes auf den Faserkern.
2 Chromatische Dispersion
Auch bei einer einwelligen Faser ist zu berücksichtigen, dass die Gruppenlaufzeit der LP 01 -Welle wellenlängenabhängig
ist (chromatische Dispersion), was die Übertragungseigenschaften beeinusst. Die
Gruppenlaufzeit der Grundwelle pro Länge ist:
= d
d!
Die Ausbreitungskonstante kann mit Gl. (32) ausgedrückt werden als
(50)
= k 0 (B(n 1 n 2 ) + n 2 ) (51)
) = d(k 0(B(n 1 n 2 ) + n 2 ))
d!
Zur Vereinfachung wird die Annahme getroen, dass die Abhängigkeit der Brechzahlen n 1 und n 2 von
! gleich ist:
dn 1
d! = dn 2
d!
) d(n 1 n 2 )
d!
) dA d ( √
n 2
N
d! = 1 n2
(52)
(53)
= 0 (54)
0 (55)
d!
Dadurch vereinfacht sich die Gleichung der Laufzeit Gl. (52) zu:
= (n 1 n 2 ) d(k 0B)
d! + d(k 0n 2 )
= n 1 n 2
d! c
)
d(V B)
dV
Die chromatische Dispersion ist die Ableitung der Laufzeit nach der Wellenlänge:
d
d = n 1 n 2
c V d2 (V B)
dV 2
} {{ }
D W
^=Wellenleiterdispersion
+ 1 c N 2 (56)
d2 n 2
(57)
}
c
{{
d 2 }
D M
^=Materialdispersion
Die chromatische Dispersion besteht damit im wesentlichen aus zwei Anteilen (Abb. 7)
1. der Wellenleiterdispersion D W und
2. der Materialdispersion D M .
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/11
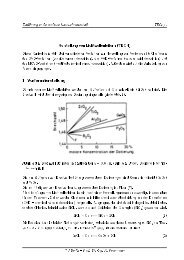
Abbildung 7: Wellenleiterdispersion D W und Materialdispersion D M einer Standard-Einmodenfaser
(aus: Voges/Petermann, Handbuch Optische Kommunikationstechnik)
Während die Materialdispersion bereits im Kapitel GRU ausführlich behandelt wurde, ergibt sich die
Wellenleiterdispersion im wesentlichen aus der Krümmung der B(V )-Charakteristik. Zur Veranschaulichung
sind in Abb. 8 die normierte Phasenkonstante B, der Term d(V B)=dV , sowie der Term
V d 2 (V B)=dV 2 als Funktion von V für die LP 01 -Welle einer Stufenfaser dargestellt.
Für einwellige Fasern mit Faserparameter V < 2; 4 ist V d 2 (V B)=dV 2 positiv und damit die Wellenleiterdispersion
negativ. Bei Wellenlängen von > 1; 3µm wird die Materialdispersion D M positiv.
Dies kann dafür genutzt werden, die Faser so zu dimensionieren, dass die Nullstelle der Gesamtdispersion
zu Wellenlängen > 1; 3µm verschoben wird. Insbesondere kann die Nullstelle der gesamten
chromatischen Dispersion zu 1; 55µm verschoben werden, wo die minimale Dämpfung erzielt
wird.
Beispiele:
1. Standard-Einmodenfaser
Eine Standard-Einmodenfaser hat beispielsweise die folgenden Dimensionierungen: a = 4µm,
= n 1 n 2
n 1
= 310 3 , bzw. n 1 n 2 = 4; 510 3 . Damit ergibt sich bei einer Wellenlänge
= 1; 55µm ein V = 1; 88 und damit gemäÿ Abb. 8 ein V d 2 (V B)=dV 2 = 0; 58, woraus sich
aus Gl. (57) eine Wellenleiterdispersion D W = 5; 6 kmnm ps ergibt, was nur zu einer teilweisen
Kompensation der Materialdispersion führt. Zur Illustration zeigt Abb. 7 für eine solche Faser
die einzelnen Anteile der chromatischen Dispersion.
2. Dispersionsverschobene Einmodenfaser
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/12
Abbildung 8: Dispersionsgröÿen der LP 01 -Grundwelle bei schwach führenden Stufenfasern (aus: Voges/Petermann,
Handbuch Optische Kommunikationstechnik)
Durch Variation der Faserparameter lassen sich auch höhere Wellenleiterdispersionswerte erzielen,
um z.B. die Materialdispersion D M = 20 kmnm ps bei = 1; 55µm vollständig zu kompensieren
oder sogar zu überkompensieren (z.B. für eine sogenannte dispersionskompensierende Faser).
Gemäÿ Gl. (57) lassen sich höhere Werte der Wellenleiterdispersion für gröÿere Brechzahlunterschiede
sowie kleinere V -Werte erreichen. So erhält man beispielsweise für eine Faserdimensionierung
mit a = 2; 4µm, = n 1 n 2
n 1
= 510 3 , bzw. n 1 n 2 = 7; 510 3 bei = 1; 55µm ein
V = 1; 46 und V d 2 (V B)=dV 2 = 1; 13, so dass sich dann eine betragsmäÿig deutlich gröÿere
Wellenleiterdispersion von D W = 18; 2 kmnm ps ergibt, mit der sich die Materialdispersion bei
= 1; 55µm im wesentlichen kompensieren lässt. Um bei den erforderlichen kleinen V -Werten
noch eine verbesserte Wellenführung zu erreichen, wird dabei häug der eigentlich lichtführende
Faserkern noch von einem Brechzahl-Ring umgeben, wie schematisch in Abb. 9 dargestellt ist.
TU Berlin Prof. Dr.-Ing. K. Petermann

Einführung in die optische Nachrichtentechnik
STU/13
= H
Abbildung 9: Schematische Darstellung des Brechzahlprols für eine dispersionsverschobene Faser
TU Berlin Prof. Dr.-Ing. K. Petermann