gesamtes Skript (PDF, 3,4 MB) - TU Berlin

Hochfrequenztechnik II 

Vorlesungsskript 

2012 

Fachgebiet Hochfrequenztechnik 

Prof. Dr.-Ing. Klaus Petermann 

überarbeitet unter Mitarbeit von 

Dr.-Ing. Christian-Alexander Bunge

Die Vorlesung Hochfrequenztechnik II beinhaltet die folgenden 

Abschnitte: 

ML: Mehrleitersysteme 

FI: Hochfrequenzfilter 

RÜ: Rückkopplung von Verstärkern 

MI: Mischer 

MOD: Modulationsverfahren 

PLL: Phasenregelkreise

Literaturhinweise 

Der gesamte Bereich der Hochfrequenztechnik wird recht umfassend dargestellt in: 

Zinke, O., Brunswig, H., (Hrsg. Von A. Vlcek u. H.L. Hartnagel): 

Lehrbuch der Hochfrequenztechnik, Band 1 und Band 2, 

Springer-Verlag Berlin, 6. Auflage bzw. 5. Auflage, 2000 bzw. 1999 

Umfassendes Handbuch über die gesamte Hochfrequenztechnik: 

Meinke, Gundlach: 

Taschenbuch der Hochfrequenztechnik, 

Springer-Verlag, Berlin, 5. Auflage 1992 

Für das Selbststudium eignet sich: 

Voges, E.: 

Hochfrequenztechnik 

Hüthig Verlag, Heidelberg, 3. Auflage 2003 

Sonstige Literatur: 

Detlefsen, I., Siart, K.: 

Grundlagen der Hochfrequenztechnik, 

Oldenbourg Verlag, 2. Auflage 2006 

Hoffmann, M.: 

Hochfrequenztechnik, ein systemtheoretischer Zugang, 

Springer-Verlag, Berlin Heidelberg 1997 

Nibler, F.: 

Hochfrequenzschaltungstechnik, 

Expert Verlag, 3. Auflage 1998 

Unger, H.G.: 

Hochfrequenztechnik in Funk und Radar, 

Teubner Verlagsgesellschaft Stuttgart, 4. Auflage 1994 

Zimmer, G.: 

Hochfrequenztechnik, Lineare Modelle (mit Windows Software), 

Springer Verlag, Berlin Heidelberg, 2000 

Best, R.E. 

Phased-Locked Loops: Design, Simulation, and Applications 

McGraw-Hill, New York, 6. Auflage 2007 

Williams, A.B., Taylor, F.J.: 

Electronic Filter Design Handbook 

McGraw-Hill, New York, 4. Auflage 2006 

Wolaver, D.H. 

Phase-Locked Loop Circuit Design 

Prentice Hall PTR, 1991 

Ein Filter-Design Programm ist frei verfügbar über: http://www.aade.com/filter.htm

Hochfrequenztechnik II Mehrleitersysteme ML/1 

Die bisher behandelten Leitungen bestanden aus 2 Leitern (Zweidrahtleitungen), wobei viele Leitungssysteme 

auch aus mehr als 2 Leitern bestehen können. Es kommt dann erwünscht (Beispiel: Richtkoppler) 

oder auch unerwünscht (Nebensprechen) zu einer Verkopplung zwischen den Leitungen. Um eine 

systematische Behandlung zu ermöglichen, sollen hier Mehrleitersysteme genauer analysiert werden. 

1 Leitungsgleichungen für Mehrleitersysteme 

Zur Veranschaulichung werde ein 3-Leiter-System gemäß Abb. 1 betrachtet. 

Abb. 1: 3-Leiter-System. 

Die einzelnen Leiter in Abb. 1 sind mit 0,1,2 bezeichnet, wobei der Leiter 0 als Masseleiter interpretiert 

werden kann. Es handelt sich somit in Abb. 1 um 2 miteinander verkoppelte Leitungen, wobei die eine 

Leitung (im folgenden Leitung 1) durch die Leiter 0,1 und die andere Leitung (im folgenden Leitung 2) 

durch die Leiter 0,2 gegeben ist, charakterisiert durch die jeweiligen Eigeninduktivitätsbeläge L ′ 11 bzw. 

L ′ 22 und die jeweiligen Kapazitätsbeläge c′ 10 bzw. c′ 20 . Das Leitungssystem in Abb. 1 enthält keine 

Verluste, die sich aber durch Berücksichtigung entsprechender Widerstands- und Leitwertsbeläge leicht 

einfügen ließen (siehe z.B. H. G. Unger, „Elektromagnetische Wellen auf Leitungen“). 

Die Verkopplung zwischen den Leitungen 1 und 2 in Abb. 1 erfolgt einerseits über den Gegeninduktivitätsbelag 

L ′ 12 (ein Teil des magnetischen Flusses von Leitung 1 durchsetzt auch Leitung 2 und 

umgekehrt) und andererseits den Koppelkapazitätsbelag c 12 ′ (Kapazität zwischen den Leitern 1,2). 

Für die Spannungs- und Stromzeiger U 1 (z), U 2 (z) bzw. I 1 (z), I 2 (z) der Leitungen 1 und 2 ergeben 

sich dann ähnlich wie im Abschnitt LEI die Leitungsgleichungen: 

dU 1 

dz 

dU 2 

dz 

= −I 1 (z)jωL ′ 11 − I 2 (z)jωL ′ 12 (1) 

= −I 1 (z)jωL ′ 12 − I 2 (z)jωL ′ 22 (2) 

TU Berlin – Prof. Dr.-Ing. K. Petermann


sowie 

dI 1 

dz 

dI 2 

dz 

= −U 1 (z)jωc ′ 10 − [ U 1 (z) − U 2 (z) ] jωc ′ 12 (3) 

= −U 2 (z)jωc ′ 20 − [ U 2 (z) − U 1 (z) ] jωc ′ 12 (4) 

Wenn man die Spannungen und Ströme in Gl. (1)-(4) zu Spaltenvektoren gemäß 

⎛ ⎞ ⎛ ⎞ 

(U) = ⎝ U 1 ⎠ , (I) = ⎝ I 1 ⎠ (5) 

U 2 I 2 

zusammenfasst, lassen sich Gl. (1)-(4) auch in Matrizenform schreiben gemäß 

d(U) 

dz 

d(I) 

dz 

mit der symmetrischen Matrix (L ′ ) der Induktivitätsbelagskoeffizienten 

(L ′ ) = 

= −jω(L ′ )(I) (6) 

= −jω(C ′ )(U) (7) 

⎛ 

⎝ L′ 11 L ′ 12 

L ′ 21 L ′ 22 

⎞ 

⎠ (8) 

mit L ′ 12 = L′ 21 

mit 

und der ebenfalls symmetrischen Matrix der Kapazitätsbelagskoeffizienten 

(C ′ ) = 

⎛ 

⎝ C′ 11 C 12 

′ 

C 21 ′ C 22 

′ 

⎞ 

⎠ (9) 

C ′ 11 = c ′ 10 + c ′ 12 ; C ′ 22 = c ′ 20 + c ′ 12 ; C ′ 12 = C ′ 21 = −c ′ 12 (10) 

2 Verallgemeinerung auf n verkoppelte Leitungen 

Wenn man das 3-Leiter-System von Abb. 1 auf ein (n+1)-Leiter-System erweitert, erhält man n 

miteinander gekoppelte Leitungen (jeweils gebildet von Leiter i = 1 . . . n mit dem Masseleiter 0), die 

auch wieder mit einem Spannungsvektor 

⎛ ⎞ 

U 1 

(U) = ⎜ 

⎝ 

. ⎟ 

(11) 

⎠ 

U n 

und einem Stromvektor 

⎛ 

(I) = ⎜ 

⎝ 

⎞ 

I 1 

. ⎟ 

⎠ 

I n 

(12) 

beschrieben werden können. Der Zusammenhang zwischen (U) und (I) ist durch die Leitungsgleichungen 

(6),(7) gegeben, wobei (L ′ ), (C ′ ) symmetrische quadratische Matrizen der Ordnung n darstellen. 



L ′ ii stellt dann den Eigeninduktivitätsbelag der Leitung i dar, während L ′ ij mit i ≠ j den Gegeninduktivitätsbelag 

zwischen den Leitungen i und j bezeichnet. Für die Matrix der Kapazitätsbelagskoeffizienten 

gilt in Verallgemeinerung von Gl. (10): 

C ′ ii = 

n∑ 

j=0,j≠i 

c ′ 

ij ; C ′ ij = −c ′ 

ij , i ≠ j (13) 

wobei c ′ 

ij den Kapazitätsbelag zwischen den Leitern i und j angibt. 

Wenn man Gl. (6) nach z ableitet und dann in Gl. (7) einsetzt, erhält man die eigentliche Wellengleichung 

d 2 (U) 

dz 2 = (A)(U) (14) 

ähnlich zur Wellengleichung der Zweidrahtleitung. Die (im allgemeinen nicht symmetrische) Matrix 

(A) ergibt sich als 

(A) = −ω 2 (L ′ )(C ′ ) (15) 

Gleichung (14) entspricht der Darstellung von n miteinander gekoppelten linearen Differentialgleichungen 

zweiter Ordnung. 

Die Lösung von Gl. (14) ergibt sich am einfachsten nach Bestimmung der Eigenwerte und zugehörigen 

Eigenvektoren. Diese Eigenwerte lassen sich auch als die neuen Eigenwellen des gesamten verkoppelten 

Mehrleitersystems interpretieren, wobei ein System mit n verkoppelten Leitungen zu genau n 

Eigenwellen führt. 

Wenn die Eigenwelle j(j = 1 . . . n) des Gesamtsystems durch die skalare Wellenamplitude w j beschrieben 

wird, so soll γ j 

deren Ausbreitungskonstante darstellen, so dass 

w j (z) = w jh (0) exp(−γ j 

z) + w jr (0) exp(+γ j 

z) (16) 

in eine hin- und rücklaufende Welle zerlegt werden kann. Es gilt damit auch 

d 2 w j 

dz 2 = γ2 j w j. (17) 

Sind die Wellenamplituden w j bekannt, ergeben sich die Spannungen als lineare Überlagerung dieser 

Wellenamplituden w j gemäß 

U i = 

n∑ 

V ij w j , (18) 

j=1 

wobei die Wichtungskoeffizienten V ij noch zu bestimmen sind. In vektorieller Form ergibt Gl. (18): 

(U) = (V )(w), (19) 

wobei die quadratische Matrix (V ) aus den Elementen V ij besteht und (w) einen Spaltenvektor mit 

den Wellenamplituden w 1 . . . w n darstellt. 

Zur Bestimmung der Matrix (V ) und der Eigenwerte γ j 

sei angenommen, es breite sich nur die j-te 

Eigenwelle des Gesamtsystems mit der Wellenamplitude w j aus. Der Spannungsvektor (U) ist dann 

gegeben als 

(U) = w j (V j ), (20) 



wobei der Spaltenvektor (V j ) die j-te Spalte der Matrix (V ) mit den Komponenten V 1j bis V nj darstellt. 

Wird Gl. (20) unter Berücksichtigung von Gl. (17) in Gl. (14) eingesetzt, ergibt sich 

d 2 (U) 

dz 2 

= (V j ) d 2 w j 

dz 2 = w jγ 2 j (V j) = (A)(U) = w j (A)(V j ). (21) 

Gl. (21) stellt ein homogenes lineares Gleichungssystem für (V j ) dar, das auch geschrieben werden 

kann als 

((A) − γ 2 j (E))(V j) = 0 (22) 

mit der Einheitsmatrix (E), das nichttriviale Lösungen nur ergibt, wenn die Koeffizientendeterminante 

verschwindet: 

) 

Det 

((A) − γ 2 j (E) = 0, (23) 

woraus die Eigenwerte γ j 

und schließlich die Eigenvektoren (V j ) bzw. die Matrix (V ) bestimmt werden 

können. 

Da dann gemäß Gl. (16) w j (z) bekannt ist, ergibt sich gemäß Gl. (18) U i (z) und schließlich mit 

Gl. (6) auch der Stromverlauf. Damit sind die Grundgleichungen für den allgemeinen Fall verkoppelter 

Mehrleitersysteme bekannt. 

3 Symmetrisches 3-Leiter-System 

Abb. 2: a) Schematische Darstellung eines symmetrischen 3-Leiter-Systems, b) Realisierung in Form 

einer Mikrostreifenleitung. 

Bei einem symmetrischen 3-Leiter-System gemäß Abb. 2 gelten für die Bezeichnungen in Abb. 1: 

c ′ 10 = c ′ 20 = c ′ ; L ′ 11 = L ′ 22 = L ′ (24) 

In diesem Fall vereinfacht sich die Analyse erheblich. Für die beiden Systemwellen ergeben sich dann 

die Gleichtaktwelle (auch gerade oder symmetrische Welle) sowie die Gegentaktwelle (auch ungerade 

oder anti-symmetrische Welle). Die Gleichtaktwelle werde durch die Spannung U S und den Strom I S 

charakterisiert, wobei bei alleiniger Ausbreitung der Gleichtaktwelle I 1 = I 2 = I S und U 1 = U 2 = U S 

gilt. Bei alleiniger Ausbreitung der Gegentaktwelle (charakterisiert durch U G und den Strom I G ) gilt 

hingegen I 1 = −I 2 = I G sowie U 1 = −U 2 = U G . 



Bei der Überlagerung von Gleich- und Gegentaktwelle gilt somit: 

U 1 = U S + U G , U 2 = U S − U G (25) 

I 1 = I S + I G , I 2 = I S − I G (26) 

beziehungsweise 

U S = 1 2 (U 1 + U 2 ), I S = 1 2 (I 1 + I 2 ) (27) 

U G = 1 2 (U 1 − U 2 ), I G = 1 2 (I 1 − I 2 ) (28) 

Beispielhafte Feldbilder für die Gleichtakt- bzw. Gegentaktstelle sind in Abb. 3 dargestellt. 

Abb. 3: Feldbilder der Gleichtaktwelle (a) und der Gegentaktwelle (b) eines symmetrischen 3-Leiter- 

Systems, — elektrisches Feld , - - - magnetisches Feld. 

Wenn man von Gl. (24) und damit auch von C ′ 11 = C′ 22 = c′ + c ′ 12 = C′ Gebrauch macht, erhält man 

durch Addition von jeweils Gl. (1), (2) und Gl. (3),(4): 

dU S 

dz 

dI S 

dz 

Nach Subtraktion von jeweils Gl. (1), (2) und Gl. (3),(4) ergibt sich: 

dU G 

dz 

dI G 

dz 

= −I S (z)jω(L ′ + L ′ 12) (29) 

= −U S (z)jω(C ′ − c ′ 12) (30) 

= −I G (z)jω(L ′ − L ′ 12) (31) 

= −U G (z)jω(C ′ + c ′ 12) (32) 

Damit sind Gleichtakt- und Gegentaktwelle voneinander entkoppelt und können sich in dem 3-Leiter- 

System unabhängig voneinander ausbreiten. Sie werden wie bei der 2-Draht-Leitung durch ihren jeweiligen 

Wellenwiderstand und ihre Ausbreitungskonstante beschrieben. Für die Gleichtaktwelle erhält 

man aus Gl. (29), (30) für den Wellenwiderstand 

Z S = 

√ 

L ′ + L ′ 12 

C ′ − c ′ 12 

(33) 



und die Ausbreitungskonstante γ S 

= jβ S 

√ 

β S = ω (L ′ + L ′ 12 )(C′ − c 12 ′ ) (34) 

Für die Gegentaktwelle ergibt sich aus Gl. (31),(32) der Wellenwiderstand 

Z G = 

√ 

L ′ − L ′ 12 

C ′ + c ′ 12 

(35) 

und die Ausbreitungskonstante γ G 

= jβ G 

√ 

β G = ω (L ′ − L ′ 12 )(C′ + c 12 ′ ) (36) 

Beispiel: Auf der Leitung breiten sich nur hinlaufende Wellen aus. Am Anfang der Leitung sei 

U 1 (z = 0) = U 10 , U 2 (z = 0) = 0 (37) 

Damit gilt: 

und es ergibt sich mit 

U S (z = 0) = U G (z = 0) = U 10 

2 

(38) 

und den Abkürzungen ∆β = β S − β G , ¯β = 1 2 (β S + β G ) 

U S (z) = U S (z = 0) exp(−jβ S z) (39) 

U G (z) = U G (z = 0) exp(−jβ G z) (40) 

( ) 

∆β 

U 1 (z) = U S (z) + U G (z) = U 10 cos 

2 z exp(−j ¯βz) (41) 

( ) 

∆β 

U 2 (z) = U S (z) − U G (z) = −jU 10 sin 

2 z exp(−j ¯βz) (42) 

Für ∆β ≠ 0 pendelt damit die Spannung zwischen den Leitungen 1 und 2 hin und her und man spricht 

von einer Vorwärtskopplung. 

Wegen der unterschiedlichen Wellenwiderstände Z S und Z G kommt es zu Reflexionen am Anfang 

und Ende des 3-Leiter-Systems, so dass auch eine Rückwärtskopplung auftritt. Tatsächlich gilt bei 

homogenem Dielektrikum (TEM-Wellen) ∆β = 0, so dass dort keine Vorwärtskopplung und nur eine 

Rückwärtskopplung auftritt. Bei Mikro-Streifenleitungen (Abb. 2b) hingegen wird durchaus ∆β ≠ 0, 

∆β ist aber immer noch klein, so dass bei normalen Richtkopplerlängen die Vorwärtskopplung klein ist 

und die Rückwärtskopplung auch dort dominiert. 

4 Mehrleitersystem mit homogenem Dielektrikum 

Falls die einzelnen Leiter in einem homogenen Medium eingebettet sind, sind alle Wellen des Gesamtsystems 

TEM-Wellen (wie bei der Zweidrahtleitung) und breiten sich mit einer gemeinsamen 

Ausbreitungskonstante γ = jβ mit 

β = ω √ µɛ (43) 



aus. Die Wellengleichung (14) vereinfacht sich dann erheblich zu 

so dass dann die Ausbreitungsmatrix (A) einfach gegeben ist als 

mit der Einheitsmatrix (E). 

d 2 (U) 

dz 2 = γ 2 (U) = −β 2 (U), (44) 

(A) = −ω 2 (L ′ )(C ′ ) = −β 2 (E) (45) 

Die Lösung von Gl. (44) ist in einfacher Weise mit hin- und rücklaufenden Wellen möglich als 

( U(z) 

) = 

( 

Uh (z = 0) ) exp(−jβz) + ( U r (z = 0) ) exp(+jβz), (46) 

wobei (U h ) bzw. (U r ) die Spannungsvektoren der hin- bzw. rücklaufenden Wellen bezeichnen. Auch 

der Stromvektor (I(z)) lässt sich dann in einfacher Weise in hin- und rücklaufende Wellen zerlegen, 

wobei aus Gl. (46) mit Gl. (7) folgt: 

( ) ω [ (Uh 

I(z) = 

β (C′ ) (z = 0) ) exp(−jβz) − ( U r (z = 0) ) exp(+jβz)] 

Ähnlich wie am Anfang vom Abschnitt SMI lassen sich dann auch die Spannungen und Ströme am Ende 

des Mehrleitersystems (Spannungsvektor (U e ), Stromvektor (I e )) mit den Spannungen und Strömen 

am Anfang (Spannungsvektor (U a ), Stromvektor (I a )) verknüpfen. Wenn man in Gl.(SMI 7,8) nur 

γ = jβ setzt, die Phasengeschwindigkeit v = ω/β entführt, Z L durch v(L ′ ) und 1/Z L durch v(C ′ ) 

ersetzt, ergibt sich für das Mehrleitersystem: 

(47) 

(U a ) = cos(βL)(U e ) + jv sin(βL)(L ′ )(I e ) (48) 

(I a ) = jv sin(βL)(C ′ )(U e ) + cos(βL)(I e ) (49) 

Mit Gl. (48), (49) ist auch eine allgemeine Impedanztransformation für Mehrleitersysteme mit homogenem 

Dielektrikum möglich. Wenn der Abschluss des Mehrleitersystems durch eine Impedanzmatrix 

(Z e ) mit (U e ) = (Z e )(I e ) gegeben ist, so lässt sich mit Gl. (48), (49) die Eingangsimpedanzmatrix 

(Z a ) mit (U a ) = (Z a )(I a ) bestimmen. Damit stellen Gl. (48), (49) eine vollständige Basis zur Beschreibung 

von beliebigen Mehrleitersystemen mit homogenem Dielektrikum dar. Die Verknüpfung in 

Gl. (48), (49) zwischen (U e ), (I e ) und (U a ), (I a ) entspricht dabei einer Kettenmatrix. Entsprechend 

den Verfahren der linearen Netzwerktheorie ist diese Kettenmatrix in jede andere Matrixdarstellung 

(z.B. Leitwert, Widerstands- oder auch Streumatrix) überführbar. Zur numerischen Berechnung ist 

dies auf einem Rechner leicht implementierbar. 

5 Symmetrisches 3-Leiter System mit homogenem Dielektrikum 

(Richtkoppler) 

Für ein symmetrisches 3-Leiter System mit homogenem Dielektrikum lässt sich die Analyse weiter 

vereinfachen. Dazu soll die Struktur mit den verkoppelten Leitungen 1,2 gemäß Abb. 4 betrachtet und 

schließlich für die Anwendung als Richtkoppler (siehe auch Abschnitt HS) analysiert werden. 



Abb. 4: Zwei verkoppelte Leitungen als Richtkoppler. 

Aufgrund des angenommenen homogenen Dielektrikums sind die Phasenkonstanten β S und β G der 

Gleichtakt- und Gegentaktwelle gleich, so dass mit Gl. (45) gilt: 

Aus Gl. (34), (36) folgt dann 

β S = β G = β = ω √ µɛ (50) 

κ L = L′ 12 

L ′ = c′ 12 

C ′ , (51) 

wobei mit κ L ein Koppelkoeffizient eingeführt wird. Gemäß Gl. (51) sind dabei für homogenes Dielektrikum 

(TEM-Koppler) die induktive und die kapazitive Kopplung gleich. 

Für die Wellenwiderstände der Gleich- und Gegentaktwelle lässt sich dann auch schreiben 

mit 

Z S = Z L 

√ 

1 + κL 

1 − κ L 

; Z G = Z L 

√ 

1 − κL 

1 + κ L 

(52) 

Z L = 

√ 

L ′ 

C ′ = √ Z S Z G (53) 

Die Spannungen an den Toren 1-4 des Kopplers in Abb. 4 werden mit einem hochgestellten Index 

bezeichnet, um sie von den Spannungen U 1 (z), U 2 (z) entlang den Leitungen 1,2 unterscheiden zu 

können. 

Am Ende des 3-Leiter-Systems (z = L) werden die Leitungen in Abb. 4 jeweils mit dem Widerstand 

Z L abgeschlossen, d.h. es soll gelten 

U (3) 

I (3) = U 1(z = L) 

I 1 (z = L) = Z L = U 2(z = L) 

I 2 (z = L) = U(2) 

I (2) (54) 

Aufgrund des symmetrischen Abschlusses werden die Gleich- und Gegentaktwellen jeweils nur im gleichen 

Wellentyp reflektiert und es ergeben sich die Abschlusswiderstände 

U S (z = L) 

I S (z = L) 

U G (z = L) 

I G (z = L) 

= U 1(z = L) + U 2 (z = L) 

I 1 (z = L) + I 2 (z = L) = Z L (55) 

= U 1(z = L) − U 2 (z = L) 

I 1 (z = L) − I 2 (z = L) = Z L (56) 



Da sich die Gleich- und Gegentaktwellen unabhängig voneinander ausbreiten, lassen sich die Impedanzen 

Z L vom Ende zum Anfang transformieren wie bei der verlustfreien Zweidrahtleitung (vergl. Gl. 

SMI 10), so dass sich unter Berücksichtigung der jeweiligen Wellenwiderstände Z S , Z G für Gleichtaktund 

Gegentaktwelle am Eingang als transformierte Impedanzen ergeben: 

U S (z = 0) 

I S (z = 0) = Z Lz S ; 

U G (z = 0) 

I G (z = 0) = Z Lz G (57) 

mit den normierten Impedanzen z S , z G , 

z S = 

√ √ 

1 + κL 

· 1 + j 1+κL 

1−κ L 

tan(βL) 

√ 

1 − κ L 1+κL 

1−κ L 

+ j tan(βL) 

(58) 

z G = 1 

z S 

(59) 

Insbesondere Gl. (59) wird natürlich nur dann so einfach, wenn die Abschlusswiderstände Z L Gl. (53) 

entsprechen. 

Ziel ist nun die Bestimmung des Eingangswiderstandes U 1 (z = 0)/I 1 (z = 0) und damit das Eigenreflexionsfaktors 

des Richtkopplers. Außerderm ist auch die Überkopplung U (4) /U (1) = U 2 (z = 0)/U 1 (z = 

0) von Interesse. 

Zunächst gilt am Tor 4 (bei Abschluss mit Z L ): 

−Z L = U 2(z = 0) 

I 2 (z = 0) = U S(z = 0) − U G (z = 0) 

I S (z = 0) − I G (z = 0) = Z U S (z = 0) − U G (z = 0) 

L 1 

z 

U 

S 

S (z = 0) − z S U G (z = 0) 

(60) 

woraus folgt: 

Für den Eingangswiderstand gilt dann: 

U S (z = 0) 

U G (z = 0) = z S (61) 

U 1 (z = 0) 

I 1 (z = 0) 

= U S(z = 0) + U G (z = 0) 

I S (z = 0) + I G (z = 0) = Z U S (z = 0) + U G (z = 0) 

L 1 

z 

U 

S 

S (z = 0) + z S U G (z = 0) 

= Z L 

U G (z = 0)(z S + 1) 

U G (z = 0)(1 + z S ) = Z L (62) 

Damit ist der Eingang reflexionsfrei angepasst und es gilt für den Streuparameter S 11 = 0 und wegen 

der Symmetrie des Kopplers in Abb. 4 auch S 22 = S 33 = S 44 = 0, wenn nur die Anschlussleitungen 

den Wellenwiderstand Z L aufweisen. 

Für die Überkopplung U 2 (z = 0)/U 1 (z = 0) ergibt sich 

U 2 (z = 0) 

U 1 (z = 0) = U S(z = 0) − U G (z = 0) 

U S (z = 0) + U G (z = 0) = z S − 1 

z S + 1 = S 41 (63) 

Wegen der Eigenreflexionsfreiheit entspricht das Verhältnis U 2 (z = 0)/U 1 (z = 0) = U (4) /U (1) dem 

Streuparameter S 41 , wobei wegen der Reziprozität und der Bausymmetrie auch S 41 = S 14 = S 32 = 

S 23 gilt. 

Damit ist das Nahnebensprechen bestimmt. Bei TEM-Leitungen soll das Fernnebensprechen (Vorwärtskopplung, 

Kopplung zwischen den Toren 1,2 bzw. 3,4) verschwinden, was durch Transformation 



vom Eingang (z = 0) zum Ausgang (z = L) in Analogie zu Gl. (8) im Abschnitt SMI (γ = jβ, L 

durch −L und Z L durch den jeweiligen Wellenwiderstand der Gleich- bzw. Gegentaktwelle ersetzen) 

gezeigt werden kann: 

U S (z = L) = cos(βL)U S (z = 0) − jZ S sin(βL)I S (z = 0) (64) 

U G (z = L) = cos(βL)U G (z = 0) − jZ G sin(βL)I G (z = 0) (65) 

Nach Einsetzen von Gl. (52), (57)-(59), (62) ergibt sich tatsächlich 

U (2) 

U (1) = U 2(z = L) 

U 1 (z = 0) = U S(z = L) − U G (z = L) 

U S (z = 0) + U G (z = 0) = 0 (66) 

und damit S 21 = 0 und wegen der Reziprozität und Symmetrie auch S 12 = S 34 = S 43 = 0 (Bei Mikro- 

Streifenleitungen mit ∆β ≠ 0 ergibt sich auch S 21 ≠ 0, was damit die Richtwirkung verschlechtert). 

Für die Übertragung von Tor 1 nach Tor 3 erhält man aus Gl. (64), (65) mit 

U (3) = U 1 (z = L) = U S (z = L) + U G (z = L) (67) 

und 

U (1) = U 1 (z = 0) = U S (z = 0) + U G (z = 0) = U S (z = 0)(1 + 1/z S ) (68) 

schließlich 

U (3) 

U (1) = 1 

√ 

cos(βL) + j sin(βL)/ 1 − κ 2 L 

= S 31 (69) 

mit 

Der Streuparameter S 41 mit 

S 31 = S 13 = S 24 = S 42 (70) 

S 41 = S 14 = S 23 = S 32 (71) 

lässt sich mit Gl. (63), (58) auch schreiben als 

S 41 = 

jκ L sin(βL) 

√1 − κ 2 L cos(βL) + j sin(βL) (72) 

in Übereinstimmung mit Gl. (HS 15). Alle anderen Streuparameter als die in Gl. (70), (71) genannten 

verschwinden, so dass sich ein idealer Richtkoppler ergibt. Die sich mit Gl. (69), (72) ergebende 

Streumatrix ist auch unitär, wie gemäß Abschnitt HS leicht nachgewiesen werden kann. 



6 Erhöhung der Bandbreite von Leitungsrichtkopplern 

Die maximale Überkopplung S 41 in einen Richtkoppler gemäß Abb. 4 erfolgt gemäß Gl. (72) für βL = 

π/2 bzw. L = λ/4. Damit ist die Kopplung in hohem Gerade frequenzabhängig. Die Bandbreite kann 

erhöht werden für einen ortsabhängigen Koppelkoeffizienten κ L (z). Ein einfaches Beispiel ist in Abb. 5 

dargestellt (siehe Meinke/Gundlach, Taschenbuch der Hochfrequenztechnik). Der dort dargestellte 

Richtkoppler entspricht der Hintereinander-Schaltung eines 3 dB- und eines 10 dB-Richtkopplers mit 

den jeweiligen Längen l 2 = l 1 = λ/4 bei der Bezugsfrequenz f = f 0 . Durch die Überlagerung entsteht 

insgesamt ein breitbandiger 5 dB-Richtkoppler. 

Abb. 5: Richtkoppler mit 2 Koppelabschnitten. 1) 3 dB-Koppler (Länge l 2 ) allein; 2) 10 dB-Koppler 

(Länge l 1 ) allein; 3) Hintereinander-Schaltung beider Koppler. 


Hochfrequenztechnik II Hochfrequenzlter FI/1 

1 Einleitung 

Bei Filtern handelt es sich um lineare (und zeitinvariante) Netzwerke, mit denen bestimmte Frequenzbereiche 

eines Eingangssignals herausgeltert werden. Man unterscheidet so beispielsweise zwischen 

Tiefpässen (Transmission nur bei tiefen Frequenzen), Hochpässen (Transmission nur bei hohen Frequenzen), 

Bandpässen (Transmission nur in einem vorgegebenen Frequenzbereich) und Bandsperren 

(Transmission nur ausserhalb eines vorgegebenen Frequenzbereichs). 

Das Filternetzwerk sei verlustfrei und reziprok. Die Quelle habe einen reellen Innenwiderstand R 1 und 

wir betrachten eine ebenfalls reelle Last R 2 gemäÿ Abb. 1. 

Abb. 1: Anordnung eines verlustlosen Filters. 

Die Betriebsdämpfungsfunktion H(s) in Abhängigkeit der komplexen Frequenz s (s = j! für reelle 

Frequenzen !) ergibt sich als 

√ 

U 2 

= 1 R 2 

: (1) 

U 1 H(s) 4R 1 

jH(j!)j 2 charakterisiert dabei die Leistungsübertragung 

jH(j!)j 2 = 

verfügbare Leistung der Quelle 

abgegebene Leistung an der Last = jU 1j 2 =(8R 1 ) 

> 1: (2) 

jU 2 j 2 =(2R 2 ) 

Die Dämpfung des Filters wird normalerweise in dB angegeben mit dem Betriebsdämpfungsmaÿ 

a b (!) = 20 ¡ lgjH(j!)jdB: (3) 

Das Filternetzwerk in Abb. 1 lässt sich auch mit Streuparametern beschreiben, was besonders einfach 

wird, wenn man den Eingang (Tor 1) auf eine Leitung mit dem Wellenwiderstand R 1 und den Ausgang 

(Tor 2) auf eine Leitung mit dem Wellenwiderstand R 2 bezieht. Der Ausgang ist dann angepasst, so 

dass sich dort nur eine hinauslaufende Wellenamplitude b 2 ergibt, während am Eingang das Signal 

durchaus reektiert werden kann, so dass sowohl I 1 als auch U 10 hin- und rücklaufende Strom- bzw. 

Spannungskomponenten beinhalten: 

U 10 = U h1 + U r 1 (4) 

I 1 = I h1 + I r 1 = 1 R 1 

(U h1 U r 1 ) (5) 

Somit gilt: 

U 1 = R 1 ¡ I 1 + U 10 = 2U h1 (6) 

TU Berlin Prof. Dr.-Ing. K. Petermann


Der Streuparameter S 21 ergibt sich somit 

S 21 = b 2 

= U 2= p √ 

R 2 

a 1 U h1 = p = U 2 4R 1 

= 1 

R 1 U 1 R 2 H(j!) 

und wegen der Reziprozität auch S 12 = S 21 = 1=H(j!). 

Unter Ausnutzung der Verlustfreiheit des Netzwerkes (Unitarität der Streumatrix) gilt für den Eigenreexionskoezienten 

= jS 11 j = jS 22 j = 

√ 

1 jS 21 j 2 = 

(7) 

√ 

1 

jH(j!)j 

jH(j!)j 

2 1 (8) 

Es ist häug auch die Gruppenlaufzeit g durch ein Filter von Interesse. Sie ist mit 

H(j!) = jH(j!)j exp ( j'(!) ) (9) 

durch 

gegeben. 

g = d'(!) 

d! 

(10) 

2 Realisierung von LC-Tiefpässen 

Die Übertragungsfunktion 1=H(s) lässt sich als Quotient eines Zähler- und eines Nennerpolynoms 

schreiben, die durch ihre jeweiligen Nullstellen in der komplexen s-Ebene charakterisiert werden (siehe 

auch Vorlesung Signale und Systeme). 

Für einige Tiefpasslter (z.B. Potenz- bzw. Butterworth, Tschebysche- oder Bessel-Thomson-Tiefpässe) 

wird die Übertragungsfunktion nur durch ein Nennerpolynom beschrieben, so dass sich dann 

die Betriebsdämpfungsfunktion H(s) schreiben lässt als 

H(s) = C 

N∏ 

n=1 

(s s xn ); (11) 

wobei N die Ordnung des Polynoms und damit des Filters angibt. C ist eine Konstante. Die Nullstellen 

s xn von H(s) (die Polstellen der Übertragungsfunktion 1=H(s)) liegen dabei in der linken s-Halbebene 

(d.h. Re(s xn ) < 0) und sind entweder rein reell oder paarweise konjugiert komplex (siehe Vorlesung 

Signale, Netzwerke und Systeme). Mögliche Realisierungen eines LC-Tiefpasslters mit H(s) gemäÿ 

Gl.(11) zeigt Abb. 2, wobei N die Anzahl der benötigten Reaktanzen angibt. Die Tore 1 und 2 wären 

wie in Abb. 1 mit der Signalquelle bzw. der Last zu verbinden. 

Oensichtlich wirken die Schaltungen in Abb. 2 als Tiefpässe, denn mit zunehmender Frequenz nimmt 

sowohl der Blindwiderstand der Serieninduktivitäten als auch der Blindleitwert der Querkapazitäten 

zu. Die genaue Wahl der Kapazitäten bzw. Induktivitäten hängt von den gewünschten Polstellen s xn 

in Gl.(11) ab. 

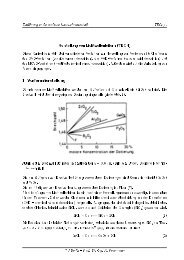
In Abb. 3 sind die Dämpfungsverläufe verschiedener Tiefpässe der Ordnung N = 5 dargestellt, wobei 

der Potenztiefpass (auch bezeichnet als Butterworth-Tiefpass) und der Tschebysche-Tiefpass durch 

Gl.(11) dargestellt und gemäÿ Abb. 2 realisiert werden. Für diese Tiefpässe gilt bei hohen Frequenzen 

(jsj js xn j) nach Gl.(11): 

jH(j!)j ! N ; (12) 



Abb. 2: Mögliche Tiefpässe verschiedener Ordnung N. 

Abb. 3: Betriebsdämpfung verschiedener Filter der Ordnung N = 5. 

was einem Dämpfungsanstieg bei hohen Frequenzen von N ¡ 6dB=Oktave entspricht. 

Für die Tiefpass-Realisierung sind verschiedene Optimierungsstrategien möglich. Beim Potenz- bzw. 

Butterworth-Tiefpass wird die Forderung nach maximal achem Dämpfungsverlauf gestellt, der durch 

jH(j!)j 2 = 1 + 

( 

! 

! G 

) 2N 

(13) 

gegeben ist (! G - 3 dB Grenzfrequenz) und sich dadurch auszeichnet, dass 

d n ( ) ∣ jH(j!)j 2 ∣∣!=0 

= 0 für n < 2N (14) 

d! n 

und damit alle Ableitungen bis zur Ordnung (2N 1) bei ! = 0 verschwinden. Der Dämpfungsverlauf 

des Potenzlters in Abb. 3 entspricht genau Gl.(13) mit N = 5. 



Die zur Realisierung des Potenzlters gemäÿ Gl.(13) sich ergebenden Pole s xn (Nullstellen von H(s) 

in Gl.(11)) liegen in der komplexen s-Ebene auf einem Halbkreis mit dem Radius ! G gemäÿ (siehe 

Signale und Systeme) 

s xn = ! G exp 

( 

j N + 2n 1 

2N 

) 

; n = 1; 2; : : : ; N: (15) 

Die in Abb. 3 eingeführte Durchlaÿgrenzfrequenz ! D bezeichnet die Frequenz, unterhalb derer die 

Dämpfung einen vorgegebenen Wert, in Abb. 3 0,1773 dB (entspricht mit Gl.(3), (7) einem = 0; 2) 

nicht überschreitet. Eine Realisierung als Tschebysche-Tiefpass (dort ist jH(j!)j 2 = 1+¡T 2 (!=! N D), 

- Konstante, T N (x) - Tschebysche-Polynom der Ordnung N) lässt im Durchlaÿbereich eine Oszillation 

der Betriebsdämpfung im vorgegebenen Toleranzbereich zu, wodurch ein steilerer Übergang zum 

Sperrbereich erzielt wird. Ein noch steilerer Übergang vom Durchlaÿ- zum Sperrbereich wird erzielt, 

wenn die Betriebsdämpfungsfunktion H(s) zusätzlich zu den Nullstellen s xn noch Pole (Nullstellen 

der Übertragungsfunktion 1=H(s)) enthält. Man gelangt dann beispielsweise zum Cauer-Tiefpass. Die 

Pole im Dämpfungsverlauf entstehen, wenn in Abb. 2 Induktivitäten durch Parallelschwingkreise oder 

Kapazitäten durch Serienschwingkreise ersetzt werden. 

Für eine Tiefpass-Anordnung nach Abb. 2 (oder ähnlich) lässt sich die Betriebsdämpfung berechnen, 

wobei die Kapazitäten und Induktivitäten so gewählt werden müssen, dass die gewünschten Pole und 

Nullstellen entstehen. Ergebnisse derartiger Rechnungen sind in Filterhandbüchern enthalten, wobei 

beispielsweise die Realisierung eines Filters 5. Ordnung mit einer maximalen Dämpfung von 0,1773 dB 

im Durchlaÿbereich ( = 0; 2) Abb. 4 entnommen werden kann (aus R. Saal, Handbuch zum Filterentwurf, 

AEG-Telefunken, 1979). 

Abb. 4 zeigt die Tiefpassrealisierung in normierter Darstellung. ist die normierte Frequenz 

= ! ! B 

(16) 

mit der Bezugsfrequenz ! B , wobei hier ! B = ! D mit der Dämpfungsgrenzfrequenz ! D gilt. Entsprechend 

gilt für die normierte komplexe Frequenz p = s=! B , und damit sind die Nullstellen s xn von H(s) 

(Polstellen der Übertragungsfunktion) durch s x = ! B ( ¦ j ) gegeben. 

Die Bauelemente-Dimensionierung bezieht sich auf gleiche Widerstände am Ein- und Ausgang R 1 = 

R 2 (r 1 = r 2 ) bzw. einer Speisung mit idealer Stromquelle (r 1 ! 1 bzw. R 1 ! 1) oder idealer 

Spannungsquelle (r 0 1 = 0 bzw. R0 1 

= 0). Die Realisierungen A und B entsprechen einander (siehe 

auch obere und untere Beschriftungszeile in Abb. 4). Die angegebenen Induktivitäten und Kapazitäten 

sind normiert, l = ! B L=R, c = ! B RC mit dem aktuellen Abschlusswiderstand R, so dass sich die 

aktuellen Induktivitäten bzw. Kapazitäten ergeben zu 

L = l R 

! B 

; C = c 

! B R 

(17) 



Abb. 4: Realisierung von Tiefpassltern 5. Ordnung als P : Potenz- oder Butterworth-Tiefpass oder 

T : Tschebysche-Tiefpass. ¢ = 17 : : : 25: Cauer-Tiefpässe unterschiedlicher Sperrdämpfung. 



Beispiel: Ein Tschebysche-Tiefpasslter (N = 5) mit der Grenzfrequenz f D = ! D =2 = 10MHz und 

< 0:2 für f < f D sei mit der unten in Abb. 2 dargestellten Schaltung und R 1 = R 2 = 50 zu 

dimensionieren. 

Aus Abb. 4 folgt: 

c 1 = c 5 = 1; 301894 l 2 = l 4 = 1; 345558 c 3 = 2; 128570 

und damit 

C 1 = C 5 = 414pF L 2 = L 4 = 1; 07H C 3 = 678pF 

Man erhält dann den in Abb. 3 dargestellten Dämpfungsverlauf. 

3 Realisierung von Hochpass, Bandpass, Bandsperre 

Filterhandbücher enthalten im allgemeinen nur die Dimensionierung von Tiefpässen, da sich der Entwurf 

von Hochpässen, Bandpässen und Bandsperren auf einen Tiefpass-Entwurf zurückführen lässt. 

Abb. 5 illustriert die Transformation eines Referenztiefpasses (Abb. 5a) mit der Bezugsfrequenz ! B 

in einen Hochpass (Abb. 5b), Bandpass (Abb. 5c) sowie eine Bandsperre (Abb. 5d). 

Tiefpass-Hochpass-Transformation Aus dem Referenz-Tiefpass in Abb. 5a ergibt sich das Hochpassverhalten 

in Abb. 5b, wenn die Frequenzen ! < ! B des Tiefpasses in die entsprechenden Frequenzen 

~! > ! B des Hochpasses abgebildet werden. Die komplette Abbildungsvorschrift zwischen der 

komplexen Frequenz j! des Tiefpasses und der komplexen Frequenz j ~! lautet 

j ~! 

! B 

= ! B 

j! bzw: ~p = 1 p 

(18) 

Damit entspricht das Dämpfungsverhalten des Hochpasses bei der Frequenz ~! = a! B exakt dem 

Dämpfungsverhalten des zugrundeliegenden Tiefpasses bei der Frequenz ! = ! B =a. Die zur Realisierung 

des Referenztiefpasses erforderlichen Induktivitäten und Kapazitäten seien bekannt. Bei der 

Transformation einer Induktivität L 0 des Referenztiefpasses muss mit Gl.(18) für seine Impedanz gelten: 

L 

Z = j!L 0 = ! 2 0 ! 

B 

= 1 

j ~! j ~!C mit C = 1 

! 2 L (19) 

B 0 

so dass eine Induktivität L 0 des Tiefpasses im transformierten Hochpass durch die Kapazität C nach 

Gl.(19) ersetzt wird. Für eine Kapazität C 0 des Referenztiefpasses gilt entsprechend 

C 

Y = j!C 0 = ! 2 0 

B 

j ~! 

! 

= 1 

j ~!L mit L = 1 

! 2 C B 0 

(20) 

so dass C 0 im transformierten Hochpass durch eine Induktivität L nach Gl.(20) ersetzt wird. Die aus 

Abb. 2 transformierten Hochpässe bestehen damit aus Längskapazitäten mit Querinduktivitäten. Die 

obigen Zusammenhänge sind in Abb. 6 tabellarisch zusammengefaÿt. 

Tiefpass-Bandpass-Bandsperre Transformation Beim transformierten Bandpass soll die Mittenfrequenz 

bei der Bezugsfrequenz ! B liegen, so dass die Frequenz ! 0 des Tiefpasses in die Frequenzen 

~! ¦! B des Bandpasses transformiert werden muss. Die Transformation erfolgt nicht nur zu 



Abb. 5: Dämpfungsverlauf eines a) Referenztiefpasses und des daraus abgeleiteten b) Hochpasses , 

c) Bandpasses sowie einer d) Bandsperre. 

~! +! B , sondern auch zu ~! ! B , da immer jH(j ~!)j = jH( j ~!)j gelten muss. Es wäre deshalb 

folgende Transformation wünschenswert: 

j! j2a(~! ! B ) für ~! +! B (21) 

j! j2a(~! + ! B ) für ~! ! B (22) 

wobei der Faktor a das Bandbreitenverhältnis zwischen dem transformierten Bandpass und dem Tiefpass 

angibt. Gl.(21),(22) gemeinsam werden relativ gut durch die Transformationsvorschrift 

j! = ja (~! ! B)(~! + ! B ) 

~! 

= a(j ~! + ! 2 B 

=j ~!) (23) 

oder in normierter Form mit p = j!=! B , ~p = j ~!=! B durch 

( ) 

p = a ~p + 1 ~p 

(24) 



Abb. 6: Transformation eines Referenztiefpasses in Hochpass,Bandpass, Bandsperre. 

erfüllt. Ähnlich wie bei der Tiefpass-Hochpass-Transformation können auch bei der Tiefpass-Bandpass- 

Transformation die Induktivitäten und Kapazitäten des Referenztiefpasses durch geeignete Reaktanzen 

ersetzt werden. Bei der Transformation einer Induktivität L 0 des Referenztiefpasses muss mit Gl.(23) 

gelten: 

Z = j!L 0 = j ~!aL 0 + a!2 B 

j ~! L 0 

! 

= j ~!L + 1 

j ~!C 

mit 

1 

L = aL 0 ; C = 

a! 2 L (26) 

B 0 

so dass eine Induktivität des Tiefpasses im transformierten Bandpass durch einen Serienschwingkreis 

ersetzt wird. Entsprechend gilt bei einer Kapazität C 0 des Referenztiefpasses: 

(25) 

Y = j!C 0 = j ~!aC 0 + a!2 B 

j ~! C ! 

0 = j ~!C + 1 

j ~!L 

(27) 



mit 

1 

C = aC 0 ; L = 

a! 2 C ; (28) 

B 0 

der damit in einen Parallelschwingkreis transformiert wird. 

Die Durchlaÿgrenzfrequenzen des Bandpasses ~! = ! ¦D ergeben sich aus der Durchlaÿgrenzfrequenz 

des Tiefpasses ! = ! B mit Gl.(23) zu: 

⎛√ 

⎞ 

! ¦D = ! B 

⎝ 1 + 1 

4a ¦ 1 ⎠ (29) 

2 2a 

so dass sich die gewünschte Durchlaÿbandbreite (! +D ! D) = ! B =a ergibt. Aufgrund der endlichen 

Güte Q der verwendeten Bauelemente (Q = !L=R, R parasitärer Reihenwiderstand bei einer 

Induktivität bzw. Q = !C=G, G parasitärer Parallelleitwert bei Kapazitäten) sind nicht beliebig kleine 

Bandbreiten realisierbar. Praktisch sollte a Q 10 : : : 100 erfüllt sein. Für kleinere Bandbreiten 

und damit höhere Güten können Quarze, keramische Filter, SAW(surface acoustic wave)-Filter oder 

unter Umständen auch Filter mit Leitungselementen eingesetzt werden. 

Bei der Tiefpass-Bandsperre Transformation gelten ähnliche Überlegungen wie beim Bandpass, wobei 

der Tiefpass gedanklich erst in einen Hochpass und dieser Hochpass dann gemäÿ obiger Bandpass- 

Transformationsbeziehungen transformiert wird. 

Die Transformationsbeziehungen sind in Tabelle 6 nochmals zusammengestellt. 

Bei der praktischen Filtersynthese wird häug gedanklich zunächst ! B = 1=s und ein Impedanzniveau 

von R = 1 zugrundegelegt. Die so normierten Induktivitäten und Kapazitäten werden dann erst zum 

Schluss gemäÿ Gl.(17) entnormiert. 

4 Positiv-Impedanz-Inverter (PII) 

Mit den vorgenannten Überlegungen ist die Synthese einer breiten Klasse von Filtern möglich. Es 

können sich aber möglicherweise Bauelementewerte ergeben, die nur schwer realisierbar sind. In diesem 

Fall kann es vorteilhaft sein, Impedanzen zu transformieren, beispielsweise mit einem Positiv-Impedanz- 

Inverter (PII). 

Abb. 7: Positiv-Impedanz-Inverter. 

Ein Positiv-Impedanz-Inverter gemäÿ Abb. 7 mit dem Bezugswiderstand R D soll einen Abschlusswiderstand 

Z e in einen Eingangswiderstand 

Z a = U a 

I a 

= R2 D 

Z e 

(30) 



transformieren, ihn also invertieren. Die Kettenmatrix des PII ist gegeben als 

⎛ 

⎝ U a 

I a 

⎞ 

⎛ 

⎠ = exp(j') 

⎝ 0 R D 

1 

R D 

0 

⎞ ⎛ 

⎠ 

⎝ U e 

I e 

⎞ 

⎠ (31) 

wobei sich mit Reaktanzen beispielsweise folgende Realisierungsmöglichkeiten (Abb. 8) ergeben: 

Abb. 8: Positiv-Impedanz-Inverter in - oder T-Schaltung 

Reaktanzen ¦jR D sind jedoch breitbandig nicht realisierbar. Eine schmalbandige Realisierung um eine 

Bezugsfrequenz ! B herum ist jedoch beispielsweise möglich gemäÿ Abb. 9. 

Abb. 9: Schmalbandige Positiv-Impedanz-Inverter. 

Für die LC-Schaltungen gilt dabei ! B L = R D = (! B C) 1 . Ein schmalbandiger PII kann auch durch 

eine =4-Leitung mit dem Wellenwiderstand Z L = R D dargestellt werden. 

Mit Hilfe eines PII ist es beispielsweise möglich, eine Kapazität in eine Induktivität oder umgekehrt zu 

transformieren. Die schmalbandige Realisierung nach Abb. 9 kann dabei durchaus ausreichend sein, 



solange es sich um die Synthese schmaler Bandlter handelt. 

5 Gekoppelte Bandlter 

Bandlter werden häug auch als miteinander verkoppelte Schwingkreise realisiert. Unter Berücksichtigung 

des Positiv-Impedanz-Inverters ist auch hier ein systematischer Entwurf möglich. 

Abb. 10: Tiefpass-Bandpass-Transformation mit gekoppelten Schwingkreisen. 

Als Beispiel wird in Abb. 10 die Transformation eines Tiefpasslters der Ordnung N = 3 in einen 

Bandpass betrachtet. Zunächst werden beim Tiefpass in Abb. 10a die Induktivität L 0 mit Hilfe von 

Positiv-Impedanz-Invertern mit den Bezugswiderständen R D = R in die Kapazitäten 

C 0 1 = L0 

R 2 (32) 

in Abb. 10b umgewandelt. Der Tiefpass von Abb. 10b hat damit die gleichen Eigenschaften wie 

der Tiefpass in Abb. 10a. Der Tiefpass von Abb. 10b wird nun mit Hilfe der Tiefpass-Bandpass- 

Transformation in einen Bandpass (Mittenfrequenz ! B , Bandbreite ! B =a) umgewandelt (vergl. Tabelle 

6), so dass sich in Abb. 10c ergibt 

C 1 = aC 0 1 ; L 10 = 

1 

a! 2 B C0 1 

; C 2 = aC 0 2 ; L 20 = 

1 

a! 2 B C0 2 

(33) 

und die Positiv-Impedanz-Inverter können schmalbandig nach Abb. 8 mit R D = R = ! B L 0 , d.h. mit 

positiven und negativen Induktivitäten 

L 0 = R ! B 

(34) 



realisiert werden. 

Durch Zusammenfassung der Induktivitäten ergibt sich dann Abb. 10d, wobei die Induktivität L 20 in 

2 parallele Induktivitäten von jeweils 2L 20 aufgeteilt ist und sich damit 

L 11 = 

( 1 

L 10 

1 

L 0 

) 

1 

und L 22 = 

( 1 

2L 20 

1 

L 0 

) 

1 

ergeben. Die beiden -Schaltungen aus Induktivitäten können bei Vergleich mit Gl.(7), (8), Abschnitt 

P als Transformatoren dargestellt werden mit 

(35) 

und M = k p L 1 L 2 mit 

beziehungsweise 

k = 

L 1 = L 11(L 22 + L 0 ) 

L 11 + L 22 + L 0 

(36) 

L 2 = L 22(L 11 + L 0 ) 

L 11 + L 22 + L 0 

(37) 

M = 

L 22 L 11 

L 11 + L 22 + L 0 

(38) 

1 

√ ( 

1 + L 0 

L 22 

)(1 + L 0 

L 11 

) : (39) 

Alternativ zur induktiven Kopplung in Abb. 10e lässt sich das Filter auch mit kapazitiver Kopplung 

entwerfen, wenn die Reaktanzen des Positiv-Impedanz-Inverters in Abb. 7 nicht mit Induktivitäten, 

sondern mit Kapazitäten realisiert werden. 

Beispiel: Aufbauend auf einen Tschebysche-Tiefpass 3. Ordnung mit maximaler Dämpfung von 

0,1773 dB ( < 0:2) im Durchlaÿbereich soll ein Bandpass mit der Mittenfrequenz f B = 10MHz 

und einer Bandbreite von 2 MHz (a = 5) für R = 50 entworfen werden. 

Nach Filterhandbuch gilt: l 0 = 1; 189469, c 0 2 

= 1; 154193 

Damit hätte der Referenztiefpass (! D = ! B = 2f B = 2 ¡ 10MHz, R = 50) 

L 0 = 947nH ; C 0 2 

= 367pF (40) 

und für den Bandpass in Abb. 10e ergibt sich mit L 10 = 134nH, L 20 = 138nH, L 0 = 796nH, 

L 11 = 161nH und L 22 = 422nH die Dimensionierung: 

C 1 = 1; 89nF ; C 2 = 1; 84nF (41) 

L 1 = 142nH ; L 2 = 293nH ; k = 0; 241 (42) 

6 Allpässe 

Allpässe haben eine konstante Dämpfung jH(j!)j = const, so dass nur die Phase ' von ! abhängt, 

was zu einer frequenzabhängigen Gruppenlaufzeit gemäÿ Gl.(10) führt. Allpässe werden eingesetzt, 

um Laufzeitverzerrungen auszugleichen. Nähere Informationen ndet man beispielsweise in 

Meinke/Gundlach: Taschenbuch der Hochfrequenztechnik, 4. Auage. 



7 Filter mit Leitungen 

Filter mit quasi-konzentrierten Elementen Die einfachste Möglichkeit zur Realisierung eines Tiefpasslters 

gemäÿ Abb. 2 besteht darin, die Kapazitäten und Induktivitäten durch kurze Leitungsstücke 

(Länge =4 im interessierenden Frequenzbereich) darzustellen, wobei Induktivitäten durch 

Leitungsstücke mit sehr hohem Wellenwiderstand √ L 0 =C 0 ( √ L 0 =C 0 Z L , Z L -Wellenwiderstand 

der Zuleitung), und Kapazitäten durch Leitungsstücke mit sehr kleinem Wellenwiderstand √ L 0 =C 0 

( √ L 0 =C 0 Z L ) realisiert werden. 

Abb. 11: Schematische Realisierungeines Tiefpasslters 5. Ordnung. 

Als Beispiel ist in Abb. 11 ein Tiefpasslter der Ordnung N = 5 in Anlehnung an Abb. 2, unten, 

skizziert. Die Kapazitäten C i und Induktivitäten L i ergeben sich mit den jeweiligen Leitungsbelägen 

C 0 i , L0 i 

und den jeweiligen Leitungslängen l i näherungsweise zu C i C 0 i 

¡ l i , L i L 0 i ¡ l i. 

Auch für Bandlter lassen sich leicht schmalbandige Leitungsrealisierungen angeben. So können für 

den Bandpass in Abb. 10c die Positiv-Impedanz-Inverter durch =4-Leitungen (vergl. Abb. 9e) und die 

3 Parallelschwingkreise durch am Ende kurzgeschlossene =4-Stichleitungen realisiert werden. 

Filter mit Leitungen jeweils gleicher Länge Eine genauere und doch einfache Analyse von Leitungsltern 

wie z.B. in Abb. 11 ist dann möglich, wenn alle vorkommenden Leitungsstücke gleich lang 

sind. 

Wenn man beispielsweise gemäÿ Abschnitt SMI eine am Ende kurzgeschlossene Leitung der Länge l 

mit dem Wellenwiderstand Z L betrachtet, gilt für die Eingangsimpedanz 

bzw. für eine verlustfreie Leitung mit = j = j!=v 

Z a = Z L tanh(l) (43) 

Z a = Z L tanh(j!l=v ) (44) 



wobei wir die komplexe Frequenz j! = s und l=v = , -Laufzeit der Leitung (Dispersion vernachlässigt), 

einführen können und sich so ergibt 

wobei S eine transformierte Frequenzebene gemäÿ 

Z a = Z L ¡ S (45) 

S = tanh(s) (46) 

angibt. Gl.(46) wird auch als Richards-Transformation bezeichnet, die sich mit 

auch schreiben lässt als 

mit 

exp(x) exp( x) 

tanh(x) = 

exp(x) + exp( x) 

S = z 1 

z + 1 

(47) 

(48) 

z = exp(2s); (49) 

wobei Gl.(49) praktisch der z-Transformation entspricht (vergleiche 'Signale und Systeme'). 

Der Grundgedanke der Filtersynthese besteht nun darin, einen Standardlterentwurf in der S-Ebene 

durchzuführen und die dort erhaltenen Elemente dann durch entsprechende Leitungsstücke in der s- 

Ebene zu ersetzen. So entspricht die Impedanz einer kurzgeschlossenen Leitung gemäÿ Gl.(45) formal 

in der S-Ebene der Impedanz einer Induktivität L = Z L . Damit lässt sich die kurzgeschlossene Leitung 

in der S-Ebene formal als Induktivität darstellen (siehe auch Abb. 12). Ähnlich lässt sich die am Ende 

leerlaufende Leitung durch eine Eingangsimpedanz 

Z a = Z L coth(l) = Z L 

S 

beschreiben und damit in der S-Ebene durch eine Kapazität C = 1=Z L darstellen. 

Ein allgemeines Leitungselement kann mit einer Kettenmatrix (siehe Seite SMI/2) beschrieben werden, 

die sich mit der Richards-Transformation schreiben lässt: 

⎛ 

⎝ U a 

I a 

⎞ 

⎠ = 

1 

p 

1 S 

2 

⎛ 

⎝ 1 SZ L 

S 

Z L 

1 

⎞ ⎛ 

⎠ 

⎝ U e 

I e 

⎞ 

(50) 

⎠ (51) 

Da sich diese Matrix in der S-Ebene nicht als einfaches Reaktanz-Netzwerk darstellen lässt, wird in der 

S-Ebene ein neues Element, das sogenannte Einheitselement (engl. unit element, abgekürzt UE) mit 

der charakteristischen Impedanz Z = Z L eingeführt, welches durch die Matrix Gl.(51) repräsentiert 

wird. Die korrespondierenden Elemente in der Leitungsebene und der Richards-Ebene sind in Abb. 12 

zusammenfassend dargstellt. 

Wenn man die komplexen Frequenzen gemäÿ s = + j! und S = u + jv beschreibt, ist der Zusammenhang 

zwischen ! (für s = j!) und der transformierten Frequenz v (für S = jv) nach Gl.(46) 

durch 

v = tan(!) (52) 

gegeben. Kleine Frequenzen v 1 in der S-Ebene entsprechen damit den Frequenzen ! 0; =; 2=; : : :, 

während groÿe v ! 1 den Frequenzen ! =2; 3=2; 5=2; : : : entsprechen. 



Abb. 12: Richards-Transformation von Schaltungselementen. 

Zur Illustration zeigt Abb. 13a den Dämpfungsverlauf eines Referenztiefpasses (Tschebysche-Tiefpass 

3. Ordnung) in der S-Ebene, woraus sich dann nach Transformation in Abb. 13b ein Leitungslter mit 

über ! periodischem Dämpfungsverlauf ergibt. So wird der Tiefpass in Abb. 13a für kleine Frequenzen 

! =2 wieder in einen Tiefpass transformiert, für ! =2 in eine Bandsperre, für ! in 

einen Bandpass usw. 

Ein Realisierungsbeispiel dafür ist in Abb. 15 dargestellt. Für den gewünschten Tschebysche-Tiefpass 

werden zunächst die Induktivitäten L 1 , L 3 , C 2 für die gewünschte Dämpfungsgrenzfrequenz v D in der 

S-Ebene bestimmt. Wenn man bei der Transformation in die Leitungsebene die Induktivitäten und 

Kapazitäten gemäÿ Abb. 12 einfach durch kurzgeschlossene bzw. leerlaufende Leitungsstücke ersetzt, 

entsteht das Problem, dass alle Leitungsstücke an der gleichen Stelle angreifen, was oft nur schwer 

realisierbar ist. 

Es ist deshalb zweckmäÿig, in das Filter Einheitselemente gemäÿ Abb. 15b einzuführen (dies entspricht 

Leitungsstücken mit dem Wellenwiderstand Z L = Z = R), die das Übertragungsverhalten des Filters 

nicht verändern. Einheitselemente mit angeschlossenen Reaktanzen können dann entsprechend Abb. 14 

umgeformt werden (Kuroda-Transformation), so dass sich schlieÿlich die in Abb. 15c dargestellte 

Realisierung in der S-Ebene ergibt. In der Leitungsrealisierung (mit der Filterdämpfung nach Abb. 13b) 

erhält man dann die Anordnung nach Abb. 15d mit drei leerlaufenden Stichleitungen. 



Abb. 13: Entwurf von Leitungsltern mit Richards-Transformation. a) Tiefpassentwurf in der S-Ebene 

(Frequenz v) und b) Dämpfungsverhalten des transformierten Filters mit Leitungselementen. 

Bei der gemäÿ obigen Überlegungen durchgeführten Filtersynthese ist zu beachten, dass Leitungswellenwiderstände 

nur in einem begrenzten Bereich realisierbar sind. Einheitselemente sind aber nicht nur 

durch einfache Leitungsstücke realisierbar, sondern auch mit verkoppelten Leitungen (Mehrleitersysteme), 

so dass sich mit verkoppelten Leitungen unter Umständen besser realisierbare Filter entwerfen 

lassen (siehe Zinke, Brunswig, Band I oder Meinke/Gundlach, Taschenbuch der Hochfrequenztechnik, 

4. Auage, Abschnitt F). 

Wenn das Filter in Abb. 11 durch Hintereinanderschaltung gleichlanger Leitungsstücke realisiert wird, 

lässt sich das in der S-Ebene als die Hintereinanderschaltung von Einheitselementen unterschiedlicher 

Impedanz Z i darstellen. Wenn U a , I a Spannung und Strom am Eingang und U e , I e Spannung und 

Strom am Ende des Filters bezeichnen, gilt für die Kettenmatrix bei N hintereinander geschalteten 

Einheitselementen (vergleiche Gl.(51)): 

⎛ 

⎝ U a 

I a 

⎞ 

⎠ = 

1 

(p 

1 S 

2 

⎛ 

∏ N 

) N 

i=1 

⎝ 1 SZ i 

S 

Z i 

1 

⎞ ⎛ 

⎠ 

⎝ U e 

I e 

⎞ 

⎠ (53) 

woraus sich die Übertragungsfunktion des Filters bestimmen lässt. Die einzelnen Wellenwiderstände 

Z i lassen sich dann so wählen, dass die gewünschten Pole und Nullstellen der Übertragungsfunktion 

in der S-Ebene entstehen. 

Insbesondere bewirkt eine =4-Leitung (dort ist S ! 1) mit dem Wellenwiderstand Z L = p R 1 R 2 

eine schmalbandige Impedanztransformation zwischen den Widerständen R 1 , R 2 . Damit stellt ein 



Abb. 14: Kuroda-Transformationen. 

Einheitselement für S ! 1 (bzw. v ! 1) einen schmalbandigen Impedanzwandler (genauer Impedanzinverter) 

dar. Zur breitbandigen Impedanztransformation um S ! 1 herum ist in der S-Ebene 

ein hochpassartiges Übertragungsverhalten erforderlich, das sich durch Analyse von Gl.(53) mit geeignet 

monoton gestuften Impedanzen Z i erreichen lässt (Eine genauere Analyse derartiger mehrstuger 

Leitungstransformatoren ndet sich in Zinke-Brunswig, Band I). 

8 SAW-Filter 

Zur Realisierung von Filtern (insbesondere Bandpassltern) im Frequenzbereich 10MHz < f < 1GHz 

werden auch oft SAW-Filter (SAW = surface acoustic wave) eingesetzt (beispielsweise Zwischenfrequenz- 

Filter in Fernsehempfängern). 

Für SAW-Filter werden piezoelektrische Kristalle (z.B. Lithiumniobat (LiNbO 3 ), Lithiumtantalat (LiTaO 3 ), 

Quarz (SiO 2 ) ) mit Interdigitalwandlern versehen, so dass eine angelegte Spannung an den Interdigitalwandlern 

zu mechanischen Verformungen an der Kristalloberäche führt, die sich dann als akustische 

Oberächenwelle (englisch abgekürzt SAW) mit einer Ausbreitungsgeschwindigkeit von typischerweise 

v a = 3000 : : : 4000m/s ausbreiten. Dies führt beim oben angegebenen Frequenzbereich 

10MHz < f < 1GHz zu akustischen Wellenlängen £ = v a =f 3m : : : 400m. 

Abb. 16 zeigt ein SAW-Filter, es besteht aus 2 Interdigitalwandlern zur Wandlung des elektrischen 

Signals in das akustische Signal und wieder zurück. 



Abb. 15: Anwendung der Kuroda-Transformation. 

Zum Verständnis des Filters ist der Interdigitalwandler genauer zu analysieren, wie er beispielsweise in 

Abb. 17 dargestellt ist. 

Eine angelegte Spannung u(t) führt zu elektrischen Feldern, wie sie durch Pfeile in Abb. 17 dargestellt 

sind. Diese Felder bewirken entsprechende mechanische Verformungen, die sich dann als SAW mit 

der Geschwindigkeit v a ausbreiten. Die Wirkung des Interdigitalwandlers lässt sich als Transversallter 

auassen, so dass sich das Ausgangssignal y (t) (mechanische Auslenkung oder dergleichen) innerhalb 

der SAW als Überlagerung der Wirkungen der einzelnen Fingerelemente darstellen lässt: 

y (t) = 

N∑ 

n=1 

( 1) n w n u(t n) (54) 

mit der Laufzeit = p=v a zwischen den Fingerelementen und dem Wichtungskoezienten w n des 

n-ten Segmentes proportional zur Überlappung der jeweiligen Fingerelektroden, siehe Abb. 17. 

Für u(t) = (t) ((t)-Dirac Impuls) erhält man aus Gl.(54) die Impulsantwort y (t) = h(t) wie sie in 

Abb. 18 skizziert ist. 

Entsprechend der Laufzeit der SAW unterhalb des Interdigitalwandlers hat die Impulsantwort eine 

endliche Dauer T = N. Wenn die Zeitskala t 0 so eingeführt wird, dass sich der Impuls von t 0 = T=2 

bis t 0 = +T=2 erstreckt und nur die Frequenzkomponenten um f 0 = 1=2 herum betrachtet werden 

kann, gilt näherungsweise aus Abb. 18: 

h(t 0 ) = w (t 0 ) cos(2f 0 t 0 ) (55) 



Abb. 16: Praktische Ausführung eines akustischen Oberächenwellenlters. 

Abb. 17: Interdigitalwandler. 

mit der quasi-kontinuierlichen Wichtungsfunktion w (t) mit w (t 0 ) = 0 für jt 0 j > T=2. 

Die Übertragungsfunktion G(j!) ergibt sich als Fouriertransformierte der Impulsantwort h(t 0 ) zu (vergleiche 

'Signale und Systeme'): 

G(j!) = 1 2 

[ 

W (j(! !0 )) + W (j(! + ! 0 )) ] ; (56) 

wobei W (j!) die Fouriertransformierte von w (t) und ! 0 = 2f 0 bezeichnet. 

Beispiel: Für gleichlange Finger des SAW-Filters sind die Wichtungskoezienten w n konstant, so dass 

sich die Wichtungsfunktion w (t 0 ) als Rechteckfunktion darstellen lässt: 

⎧ 

⎨ 

w (t 0 ) = 

⎩ 

1 jt 0 j < T 2 

0 jt 0 j > T 2 

so dass sich für die Übertragungsfunktion ergibt (vergleiche 'Signale und Systeme') 

⎡ 

G(j!) = T ( 

⎣ T si 

2 2 (! ! 0) 

) 

(57) 

+ si 

( 

T 

2 (! + ! 0)) ⎤ ⎦ (58) 

mit si(x) = sin(x)=x. Solange wir ein schmalbandiges Filter mit T ! 0 1 betrachten und uns auf 

positive Frequenzen beschränken, ist der zweite si-Term vernachlässigbar und wir erhalten: 

G(j!) ∣ ∣ 

!>0 

T 2 si(T (f f 0)) (59) 



Abb. 18: Impulsantwort (schematisch) eines Interdigitalwandlers. 

und es ergibt sich als 4 dB-Bandbreite B (Argument der si-Funktion = =2): 

B = 1 T = 2f 0 

N ; (60) 

die damit genau umgekehrt proportional ist zur Laufzeit der SAW unterhalb des Interdigitalwandlers. 

Die oben angegebene Übertragungsfunktion beinhaltet nur die Wandlung vom elektrischen ins akustische 

Signal, so dass die komplette Übertragungsfunktion (elektrisch - akustisch - elektrisch) durch 

G 2 (j!) beschrieben wird (Annahme gleicher Interdigitalwandler am Ein- und Ausgang) und die Bandbreite 

B gemäÿ Gl.(60) dann der 8 dB-Bandbreite entsprechen würde. 

Beim kompletten SAW-Filter ist zusätzlich noch die elektrische Beschaltung und insbesondere die 

Kapazität der Interdigitalwandler zu berücksichtigen. 


Hochfrequenztechnik II Rückkopplung von Verstärkern RÜ/1 

Durch Rückkopplung kann ein Verstärker stabilisiert werden, er kann aber auch instabil werden und 

anfangen zu schwingen. Auch Oszillatoren stellen im Prinzip rückgekoppelte Verstärker dar. 

1 Breitbandverstärker 

Eine Anwendung für Verstärker mit Rückkopplung besteht in der Realisierung von Breitbandverstärkern. 

Als Beispiel werde ein Transimpedanzverstärker betrachtet, wie er in Abb. 1 dargestellt ist. 

Abb. 1: Prinzip eines Transimpedanzverstärkers mit bipolarem Transistor. 

Bei einem Transistor mit sehr hoher Strom- und Spannungsverstärkung ergibt sich näherungsweise 

U A ≈ −R K · I 1 , wobei R K dann als Transimpedanz bezeichnet wird. 

Durch den Rückkoppelwiderstand R K wird auch die Bandbreite des Verstärkers beeinflusst, wie im 

folgenden diskutiert werden soll. Die Koppelkapazität C K sei sehr groß (C K → ∞) und der Ausgang, 

abgesehen vom Widerstand R L , unbelastet, so dass sich aus Abb. 1 folgendes „Hochfrequenzschaltbild” 

1 ergibt. 

Abb. 2: „Hochfrequenzschaltbild” des Transimpedanzverstärkers aus Abb. 1. 

Der Bipolartransistor werde durch ein vereinfachtes Giacoletto-Ersatzschaltbild beschrieben: 

Dabei ist c csp die differentielle Kollektor-Basis-Sperrschichtkapazität, r e der differentielle Widerstand 

1 Im Hochfrequenzschaltbild stellen Gleichspannungen Kurzschlüsse dar, und die Einstellung des Arbeitspunktes wird 

nicht beachtet. 



Abb. 3: Vereinfachtes Giacoletto-Ersatzschaltbild eines Bipolar-Transistors. 

der Basis-Emitter-Diode (r e = (kT/e)/I E , I E – Emitterstrom, k – Boltzmann-Konstante, T – absolute 

Temperatur, e – Elementarladung) und r e ′ = r e /β 0 (β 0 – Gleichstromverstärkung in Emitterschaltung) 

und c e ′ = 1/(r e · ω T ) mit der Transitfrequenz f T = ω T /2π. 

Damit folgt aus Abb. 2 und 3 das Ersatzschaltbild des Verstärkers. 

Abb. 4: Ersatzschaltbild des Verstärkers aus Abb. 1. 

Unter der Voraussetzung, dass für den Strom im Rückkoppelzweig gilt |I K | ≪ |I RL |, ergibt sich 

näherungsweise 

mit der inneren Verstärkung 

U A = −U 1 

R L 

r e 

= −U 1 · v i (1) 

v i = R L 

r e 

(2) 

Da U 1 und U A damit in einfacher Weise miteinander verknüpft sind, genügt es, für die Bestimmung 

der gesamten Übertragungsfunktion die Übertragungsfunktion von U G nach U 1 zu bestimmen. 

Unter Anwendung des Miller-Effektes (Miller-Kapazität) lassen sich R K und c csp aus dem Rückkoppelzweig 

transformieren, so dass sich der Eingangszweig gemäß Abb. 5 ergibt. 

Abbildung 5 lässt sich schließlich vereinfachen zu Abb. 6. 

Dabei stellt R ′ mit 

1 

R ′ = 1 r ′ e 

+ 1 + v i 

R K 

(3) 



K 

Abb. 5: Ersatzschaltbild des Eingangszweigs des Verstärkers aus Abb. 1. 

Abb. 6: Vereinfachtes Ersatzschaltbild des Eingangszweigs des Verstärkers aus Abb. 1. 

die Parallelschaltung aus r ′ e und R K 

1+v i 

dar und 

C ′ = c ′ e + c csp (1 + v i ). (4) 

Abbildung 6 stellt einen Tiefpass 1. Ordnung dar gemäß: 

U 1 

U G 

= 

R ′ 

R ′ + R G 

1 

1 + jω/ω g 

mit ω g = 1 C ′ ( 

1 

R ′ + 1 

R G 

) 

(5) 

Die Grenzfrequenz ω g repräsentiert damit die Bandbreite des Breitbandverstärkers. Mit Gl. (1) und 

(2) gilt dann für die gesamte Übertragungsfunktion: 

mit der Verstärkung v m bei kleinen Frequenzen 

U A U 

= −v 1 v m 

i = − 

(6) 

U G U G 1 + jω/ω g 

v m = 

R L R ′ 

r e (R ′ + R G ) 

(7) 

Sowohl die Bandbreite ω g als auch die Verstärkung v m hängen von R ′ und damit vom Rückkoppelwiderstand 

R K ab. Von Interesse ist dabei das Verstärkungs-Bandbreite-Produkt 

v m · ω g = 

R L 

r e R G C ′ = 

1 

1 R G 

ω T R L 

+ c csp R G (1 + re 

R L 

) , (8) 

das unabhängig von R ′ und damit auch unabhängig vom Rückkoppelwiderstand R K wird. Durch Wahl 

von R K kann somit entweder ein Breitbandverstärker hoher Verstärkung und kleiner Bandbreite oder 

geringer Verstärkung und hoher Bandbreite realisiert werden. 



Zahlenbeispiel: Als Beispiel sei angenommen R G = R L = 50 Ω, r e = 2, 5 Ω (Emitterstrom I E = 

10 mA), c csp = 0, 5 pF und f T = ω T 

2π 

= 5 GHz. Es ergibt sich dann ein Verstärkungs-Bandbreite- 

Produkt von v m · f g = v m ω g /(2π) ≈ 2, 75 GHz. Weiterhin ergibt sich mit β 0 = 30 und R K = 

3, 15 kΩ beispielsweise ein v m ≈ 10 und R ′ ≈ 50 Ω, so dass sich dann ein Breitbandverstärker 

mit der Bandbreite f g = 275 MHz und einer Verstärkung von 20 dB ergibt, der eingangsseitig 

reflexionsfrei an eine Leitung mit einem Wellenwiderstand Z L = 50 Ω angepasst ist. 

Abb. 7 zeigt das Beispiel eines Breitbandverstärkers mit f g ≈ 10 GHz basierend auf einem GaAs- 

MESFET. Die schwarzen Balken in Abb. 7 stellen Streifenleitungs-Elemente auf der Leiterplatte dar 

(oben Leiterbreite, unten Leiterlänge, jeweils in mm). 

Abb. 7: Breitbandverstärker (10 GHz) mit einem GaAs-MESFET (Quelle:Dissertation M. Martin, TU 

Berlin 1987). 

2 Beschreibung rückgekoppelter Verstärker 

Zur systematischen Beschreibung rückgekoppelter Netzwerke betrachten wir Abb. 8 . 

Abb. 8: Rückgekoppeltes Netzwerk mit Verstärkung V und Rückkopplung K. 

Der Verstärker wird durch die Übertragungskunktion V charakterisiert mit 

B = V · A, (9) 

wobei A und B die Zeiger (bzw. Fouriertransformierten) von Spannungen, Strömen oder Wellenamplituden 

am Eingang und Ausgang des Netzwerkes darstellen. Die Übertragungsfunktion K des 



Rückkoppelnetzwerks wird durch 

A ′′ = K · B (10) 

charakterisiert, so dass sich unter Berücksichtigung des Summationspunkts am Eingang A = A ′ + A ′′ 

ergibt: 

B = V · A = V (A ′ + A ′′ ) = V (A ′ + KB) (11) 

und damit 

B = V ′ · A ′ (12) 

mit 

V ′ = 

V 

1 − KV . (13) 

V ′ stellt damit die effektive Verstärkung das rückgekoppelten Verstärkers dar. 

• Für |1 − K · V | < 1 gilt |V ′ | > |V |. Wir sprechen dann von einer „Mitkopplung”. 

• Für |1 − K · V | > 1 gilt |V ′ | < |V |. Wir sprechen dann von einer „Gegenkopplung”. 

• Für K · V = 1 geht V ′ → ∞, so dass dann der Verstärker anfängt zu schwingen. Wir sprechen 

dann von einem „Oszillator”. 

Bei gegengekoppelten Systemen ist der Sonderfall sehr starker Gegenkopplung von Interesse mit |1 − 

K · V | ≫ 1, woraus sich dann mit Gl. (13) 

V ′ ≈ − 1 K 

für |1 − K · V | ≫ 1 (14) 

ergibt. Die Verstärkung ist dann nur noch von dem (z. B. passiven) Rückkoppelnetzwerk abhängig. 

Weiterhin kann z. B. durch Gegenkopplung die Bandbreite eines Breitbandverstärkers erhöht werden. 

Wenn wir für V ähnlich zu Gl. (6) 

v m 

V = − 

(15) 

1 + jω/ω g 

und K = K als reell und frequenzunabhängig annehmen, ergibt sich 

V ′ v m 1 

= − 

mit ω gr = ω g (1 + Kv m ), (16) 

1 + K · v m 1 + jω/ω gr 

so dass, wie schon oben diskutiert, die Bandbreite zwar erhöht werden kann, aber das Verstärkungs- 

Bandbreite-Produkt konstant bleibt. 

Das Verstärker-Netzwerk kann in verschiedener Weise mit dem Rückkoppelnetzwerk verschaltet werden. 

Es ergeben sich dann die vier Anordnungen gemäß Abb. 9. 

Der im oberen Abschnitt 1 diskutierte Transimpedanzverstärker gemäß Abb. 4 stellt dabei beispielsweise 

ein Netzwerk mit Parallel-Parallel-Rückkopplung (siehe Abb. 9d) dar, wie Abb. 10 verdeutlicht. 



a) b) 

c) d) 

Abb. 9: Möglichkeiten der Verschaltung eines Verstärkers mit einem Rückkoppelnetzwerk: a) Serien- 

Parallel-Rückkopplung mit V = U 2 /U 1 , K = −U ′′ 

1/U 2 , V ′ = U 2 /U ′ 1; b) Serien-Serien-Rückkopplung 

mit V = I 2 /U 1 , K = −U ′′ 

1/I 2 , V ′ = I 2 /U ′ 1; c) Parallel-Serien-Rückkopplung mit V = I 2 /I 1 , 

K = −I ′′ 

1/I 2 , V ′ = I 2 /I ′ 1 und d) Parallel-Parallel-Rückkopplung mit V = U 2 /I 1 , K = −I ′′ 

1/U 2 , 

V ′ = U 2 /I ′ 1. 

Abb. 10: Transimpedanzverstärker als Netzwerk mit Parallel-Parallel-Rückkopplung. 



3 Stabilität von rückgekoppelten Netzwerken 

Rückgekoppelte Netzwerke bergen das Problem möglicher Instabilität. So kann z. B. aus einer erwünschten 

Gegenkopplung durch auftretende Phasendrehungen eine unerwünschte Mitkopplung werden. 

Wie bei jedem Netzwerk muss auch ein rückgekoppeltes Netzwerk die Bedingung erfüllen, dass die 

Übertragungsfunktion V ′ (s) (s – komplexe Frequenz s = jω + σ der Laplace-Transformation) keine 

Polstellen in der rechten komplexen s-Halbebene (R(s) ≥ 0) aufweisen darf. 

3.1 Stabilitätskriterium nach Strecker-Nyquist 

Wir nehmen zunächst an, der Verstärker ohne Rückkopplung sei stabil, d. h. V (s) habe keine Pole in 

der rechten s-Halbebene. Damit dann V ′ (s) gemäß Gl. (13) auch stabil ist, darf auch V ′ (s) keine Pole 

in der rechten s-Halbebene aufweisen, d. h. 

für alle R(s) ≥ 0 muss K · V ≠ 1 

sein. Dazu ist es zweckmäßig, die konforme Abbildung von der komplexen s-Ebene in die komplexe 

K · V -Ebene zu betrachten, wie sie Abb. 11 zeigt. 

Abb. 11: Konforme Abbildung der komplexen s-Ebene in die K · V -Ebene. 

Der Bereich R(s) > 0 wird begrenzt durch die imaginäre Achse s = jω. Die Abbildung dieser Geraden 

s = jω in die K · V -Ebene (auch als „Ortskurve” bezeichnet) ist in Abb. 11 skizziert. Die konforme 

Abbildung ist im kleinen winkeltreu, so dass die rechte s-Halbebene in den schraffierten Bereich der 

K · V -Ebene abgebildet wird. Nun muss für stabiles Verhalten für alle R(s) ≥ 0 ein K · V ≠ 1 gelten, 

so dass der schraffierte Bereich in der K · V -Ebene den Punkt „+1” nicht beinhalten darf. 



Damit lässt sich das Strecker-Nyquist-Kriterium wie folgt formulieren: 

Für stabiles Verhalten darf die Ortskurve (K · V )(jω) den Punkt „+1” nicht umschließen. 

Der rückgekoppelte Verstärker in Abb. 11 wäre also stabil. 

Beispiel: Gegenkopplung über mehrere Verstärkerstufen. 

Wir nehmen an, der Verstärker mit der Übertragungsfunktion V besteht aus n hintereinander 

geschalteter Stufen, die jeweils die Charakteristik eines Tiefpasses 1. Ordnung aufweisen, und 

die Rückkopplung K sei reell und frequenzunabhängig mit K = K, d. h.: 

K · V = −K · v m 

1 

(1 + j ω ω g 

) n . (17) 

Für n ∈ {1, 3} ist die Ortskurve (K · V )(jω) in Abb. 12 dargestellt (für n = 1 ergibt sich ein 

Kreis), während n = 2 der Darstellung in Abb. 11 entspricht. 

a) b) 

Abb. 12: Ortskurven (K · V )(jω) für gegengekoppelte Verstärker mit a) 1 Stufe (n = 1) und b) 3 

Stufen (n = 3) entsprechen Gl. (17). Kurve durchgezeichnet für ω > 0 und gestrichelt für ω < 0. 

Für n ∈ {1, 2} bleibt das Verhalten immer stabil, während bei n = 3 die Ortskurve den Punkt 

„+1” für K · v m ≥ 8 umschließt und damit der Verstärker instabil wird und anfängt zu schwingen. 

Das Problem bei der Rückkopplung über mehrere Stufen besteht darin, dass aus der gewünschten 

Gegenkopplung dann auf Grund der zusätzlichen Phasendrehung bei höheren Frequenzen eine Mitkopplung 

mit der entsprechenden Schwingneigung werden kann. 

3.2 Stabilitätskreis und Stabilitätsfaktor 

Allein durch die innere Rückkopplung, ausgedrückt durch den y-Parameter y 12 

, kann ein Verstärker 

instabil werden. Zur Untersuchung dieser Instabilität wird ein Verstärker, beschrieben durch seine y- 

Parameter, betrachtet, der mit der Lastadmittanz y L 

abgeschlossen ist (siehe Abb. 13). 



Abb. 13: Verstärker mit y-Parameterm und Lastadmittanz y L 

. 

Es soll nun die Eingangsadmittanz y E 

= I 1 

U 1 

dabei instabil werden, wenn R(y E 

) < 0 wird. 

des Verstärkers ermittelt werden. Ein Verstärker kann 

Für den Eingangskreis gilt: 

I 1 = y 11 

U 1 + y 12 

U 2 (18) 

und für den Ausgangskreis ergibt sich 

und damit 

0 = (y 22 

+ y L 

)U 2 + y 21 

U 1 (19) 

U 2 = − y 21 

y 22 

+ y L 

U 1 . (20) 

Wir können so U 2 in Gl. (18) eliminieren, und aus Gl. (18) ergibt sich: 

( 

I 1 = y 11 

− y 21 y ) 

12 

U 

y 22 

+ y 1 (21) 

L 

und damit die zu untersuchende Eingangsadmittanz y E 

y E 

= I 1 

U 1 

= y 11 

− y 21 y 12 

y 22 

+ y L 

(22) 

Für R(y E 

) < 0 kann der Verstärker instabil werden, da dann der Verstärkereingang nicht mehr Energie 

aufnimmt, sondern Energie abgibt. Um nun zu erkennen, für welche Lastadmittanzen y L 

diese 

Instabilität auftreten kann, wird Gl. (22) nach y L 

aufgelöst: 

y L 

= −y 22 

− y 12 y 21 

y E 

− y 11 

. (23) 

Diese Beziehung lässt sich auffassen als eine konforme Abbildung von der komplexen Ebene der Eingangsadmittanz 

y E 

in die komplexe Ebene der Lastadmittanz y L 

. Insbesondere ist von Interesse, wohin 

die linke Halbebene von y E 

(mit R(y E 

) < 0 – also instabil) abgebildet wird (siehe Abb. 14). Die linke 

Halbebene der y E 

-Ebene wird damit in einen Kreis in der y L 

-Ebene abgebildet. Dieser Kreis wird als 

sog. „Stabilitätskreis” bezeichnet. Lastadmittanzen außerhalb dieses Stabilitätskreises führen damit zu 

einem stabilen Verstärkerverhalten, während Lastadmittanzen innerhalb dieses Kreises zu R(y E 

) < 0 

und damit zu instabilem Verhalten führen können. 

Passive Lastadmittanzen haben stets R(y L 

) > 0. Ein Verstärker wird als absolut stabil bezeichnet, 

wenn für derartige passive Lastadmittanzen immer auch R(y E ) > 0 gilt. Dies bedeutet, dass ein 



Abb. 14: Konforme Abbildung der linken y E 

-Halbebene in einen Kreis (Stabilitätskreis) in der y L 

- 

Ebene. 

Verstärker immer genau dann absolut stabil ist, wenn der Stabilitätskreis in der linken Halbebene der 

y L 

-Ebene liegt. Um eine Bedingung für die absolute Stabilität eines Verstärkers herzustellen, nehmen 

wir zunächst an, dass es doch irgendeine Lastadmittanz y L 

mit R(y L 

) > 0 gäbe, für die R(y E 

) = 0 

wird: 

( ) 

R(y E 

) = ! y 

0 = R(y 11 

) − R 12 

y 21 

. (24) 

y 22 

+ y L 

Um die beiden R()-Ausdrücke besser auswerten zu können, schreiben wir y 12 

y 21 

und (y 22 

+ y L 

) nach 

Betrag und Phase 

Damit ergibt sich in Gl. (24): 

und damit 

y 12 

y 21 

= |y 12 

y 21 

| exp(jϕ) 

y 22 

+ y L 

= |y 22 

+ y L 

| exp(jϕ 2 ) = R(y 22 + y L ) 

cos(ϕ 2 ) 

exp(jϕ 2 ). 

cos(ϕ 2 ) 

0 = R(y 11 

) − |y 12 

y 21 

| 

R(y 22 

+ y L 

) cos(ϕ − ϕ 2) 

R(y 11 

)R(y 22 

+ y L 

) = |y 12 

y 21 

| cos(ϕ 2 ) cos(ϕ − ϕ 2 ) 

Diese Beziehung lässt sich auch schreiben als 

= 1 2 |y 12 y 21 |[cos(ϕ) + cos(2ϕ 2 − ϕ)]. 

R(y 11 

)R(y 22 

+ y L 

) = 1 2 R(y 12 y 21 ) + 1 2 |y 12 y 21 | cos(2ϕ 2 − ϕ). 

Diese Gleichung ist offenbar bei R(y L 

) > 0 und beliebiger Phase ϕ 2 nur erfüllbar, wenn die folgende 

Ungleichung gilt (wir setzen dabei ein R(y 11 

) > 0 voraus): 

R(y 11 

)R(y 22 

) < 1 2 [R(y 12 y 21 ) + |y 12 y 21 |]. 



Ist diese Gleichung nicht erfüllt, wenn also 

R(y 11 

)R(y 22 

) > 1 2 [R(y 12 y 21 ) + |y 12 y |] (25) 

21 

gilt, ist für beliebige Lastadmittanzen mit R(y L 

) > 0 eine Eingangsadmittanz R(y E 

) = 0 nicht 

möglich, so dass Gl. (25) die Bedingung dafür angibt, dass der Stabilitätskreis in der linken y L 

- 

Halbebene liegt. Damit ist unter der Voraussetzung von Gl. (25) der Verstärker absolut stabil. 

Zur Charakterisierung der Stabilität wird häufig ein Stabilitätsfaktor k eingeführt gemäß: 

k = 2R(y 11 )R(y 22 ) − R(y 12 y 21 ) . (26) 

|y 12 

y 21 

| 

Die Bedingung für absolute Stabilität nach Gl. (25) entspricht dabei k > 1. Für k < 1 ist der Verstärker 

nur bedingt stabil. Der Stabilitätsfaktor k kann auch mit Streuparametern formuliert werden: 

k = 1 + |S 11S 22 − S 12 S 21 | 2 − |S 11 | 2 − |S 22 | 2 

. 

2|S 12 S 21 | 

Abschließend soll noch ohne Beweis die maximale Verstärkung G ′ m bei eingangs- und ausgangsseitiger 

Anpassung angegeben werden: 

∣ G m ′ y ∣∣∣∣ ( 

= 

21 

k − √ ∣ 

) 

k 

∣y y ∣∣∣∣ 

− 1 = 

21 

1 

∣ 

12 

y 12 k + √ , 

k 2 − 1 

k > 1. (27) 

Für k < 1 darf der Verstärker natürlich nicht eingangs- und ausgangsseitig angepasst werden, da er 

sonst anfängt zu schwingen. 

4 Oszillatoren 

Ein rückgekoppeltes Netzwerk wird zum Oszillator, wenn K · V = 1 wird. In diesem Sinn gibt es eine 

große Vielfalt bei der Realisierung von Oszillatoren. 

Abb. 15: Hochfrequenzschaltbild eines Oszillators mit den Reaktanzen X 1 , X 2 und X 3 . 

Als Beispiel wollen wir einen LC-Oszillator entsprechend Abb. 15 betrachten. X 1 , X 2 und X 3 stellen 

dabei Reaktanzen, also z. B. Induktivitäten oder Kapazitäten, dar. Wenn der FET in Abb. 15 nur durch 



Abb. 16: Ersatzschaltbild des Oszillators von Abb. 15. 

seine Steilheit S charakterisiert wird (keine Rückwirkung, Eingangs- und Ausgangsimpedanzen → ∞), 

ergibt sich das Ersatzschaltbild in Abb. 16. 

Die Anschwingbedingung für den Oszillator in Abb. 16 ergibt sich wahlweise aus K · V 

! = 1 oder der 

Bedingung det(y) = y 11 

y 22 

− y 12 

y 21 

= 0 (wenn man die y-Parameter der Anordnung in Abb. 16 

bestimmt) oder aus folgender anschaulicher Überlegung: 

In Abb. 16 gilt für die Verstärkung 

U 2 

= − S U 1 Y , (28) 

wobei Y der Parallelschaltung von jX 3 mit R L und der Serienschaltung von jX 1 und jX 2 entspricht: 

Y = 1 + 1 1 

+ . (29) 

jX 3 R L jX 1 + jX 2 

Andererseits gilt für die Rückwirkung vom Ausgang zum Eingang der Spannungsteiler 

U 1 

U 2 

= 

X 1 

X 1 + X 2 

. (30) 

Die Multiplikation von Gl. (28) und (30)führt dann auf die Anschwingbedingung: 

U 1 

U 2 

U 2 

U 1 

! 

= 1 = − S Y 

Um Gl. (31) zu erfüllen, muss zunächst Y reell sein, so dass gelten muss: 

und damit 

X 1 

X 1 + X 2 

. (31) 

1 1 ! 

+ 

= 0 (32) 

jX 3 jX 1 + jX 2 

X 1 + X 2 + X 3 

! 

= 0. (33) 

Gl. (33) stellt die Phasenbedingung für das Anschwingen des Oszillators dar. Mit Gültigkeit von Gl. 

(33) wird Y = 1 

R L 

und X 1 + X 2 = −X 3 , so dass sich aus Gl. (31) ergibt: 

S · R L · X1 

X 3 

! 

= 1 (34) 

Die Steilheit S in Gl. (34) gibt die Steilheit an, die mindestens erforderlich ist, damit der Oszillator 

anschwingt (Anschwingsteilheit). Weiterhin zeigt Gl. (34), dass X 1 und X 3 das gleiche Vorzeichen und 

damit den gleichen Reaktanztyp (z. B. beide Reaktanzen induktiv oder beide Reaktanzen kapazitiv) 

aufweisen müssen. 

Es ergeben sich dann grundsätzlich zwei Möglichkeiten: 



induktive Dreipunktschaltung 

Hier sind X 1 und X 3 induktiv mit X 1 = ωL 1 und X 3 = ωL 3 und jX 2 = 1 

jωC 2 

, woraus sich die 

Schwingfrequenz ω 0 zu 

ω0 2 = 1 ( ) 

1 

C 2 L 1 + L 3 

und die Anschwingsteilheit aus Gl. (34) zu 

ergeben. 

kapazitive Dreipunktschaltung 

S = 1 

R L 

L 3 

L 1 

Hier sind X 1 und X 3 kapazitiv mit jX 1 = 1 

jωC 1 

und jX 3 = 1 

jωC 3 

und X 2 induktiv mit X 2 = ωL 2 . 

Es ergeben sich dann ω 0 aus Gl. (33) zu 

und die Anschwingsteilheit aus Gl. (34) zu 

ω 2 0 = 1 L 2 

( 1 

C 1 

+ 1 C 3 

) 

S = 1 

R L 

C 1 

C 3 

Die kapazitive Dreipunktschaltung wird auch als Colpitts-Oszillator bezeichnet. Der Vorteil gegenüber 

der induktiven Dreipunktschaltung besteht darin, dass nur eine Induktivität benötigt wird, wobei diese 

Induktivität z. B. auch durch einen Schwingquarz (der sich dann im induktiven Arbeitspunkt befindet) 

realisiert werden kann. 

Ein Realisierungsbeispiel für einen Colpitts-Oszillator mit bipolarem Transistor zeigt Abb. 17. 

Abb. 17: Schaltungsbeispiel für einen Colpitts-Oszillator. 


Hochfrequenztechnik II Mischer MI/1 

Das Ziel eines Mischers besteht darin, ein Signal einer Frequenz ! 1 auf eine andere Frequenz ! 2 

umzusetzen. 

Beispielsweise liegt das Eingangssignal von einer Antenne bei einer hohen Frequenz vor, welches dann 

zur einfacheren Signalverarbeitung auf eine kleinere Frequenz umgesetzt werden soll. Diese Funktion 

wird von einem sog. Mischer vorgenommen. 

1 Mischprinzipien 

Das Prinzip eines Mischers besteht darin, das Eingangssignal mit einem Lokal-Oszillator-Signal zu 

multiplizieren, wie in Abb. 1 schematisch dargestellt ist. 

Eingangssignal 

u s (t) u ZF (t) 

Zwischenfrequenzsignal 

ω 1 ω z = |ω 0 − ω 1 | 

ω 0 

Lokaloszillator 

Abb. 1: Grundprinzip eines Mischers. 

Wir nehmen zunächst ein harmonisches Eingangssignal u s (t) an: 

u s (t) = < [ U S exp(j! 1 t) ] = Û S cos(! 1 t + ' 1 ) = 1 2 

Der Zeiger U S ist dabei durch U S = 

Frequenz ! 0 , 

u 0 (t) = 1 2 

[ 

US exp(j! 1 t) + U £ S exp( j! 1t) ] (1) 

Û S exp(j' 1 ) charakterisiert. Der Lokaloszillator hat die feste 

( 

) 

Û 0 exp(j! 0 t) + c:c: ; (2) 

wobei c:c: für konjugiert komplex (engl. conjugate complex) steht. Der Mischer vollzieht eine Multiplikation 

von u 0 (t) und u s (t): 

u s (t) ¡ u 0 (t) = 1 { [ ] [ 

Û 0 U S exp[j(! 0 + ! 1 )t] + c:c + Û 0 U £ S exp[j(! 0 ! 1 )t] + c:c:] } (3) 

4 

Nach der Multiplikation entstehen damit Signale sowohl bei der Summenfrequenz (! 0 + ! 1 ) als auch 

bei der Dierenzfrequenz (! 0 ! 1 ). Wir gehen zunächst von einem Mischer aus, der das Eingangssignal 

von einer hohen Frequenz ! 1 auf eine niedrige Frequenz ! z = j! 0 ! 1 j, der sogenannten 

Zwischenfrequenz, umsetzt. Es wird dann nur die Dierenzfrequenz aus Gl. (3) verwendet (nach 

entsprechender Filterung), so dass sich für das Zwischenfrequenzsignal ergibt: 

u ZF (t) = A 1 Û 0 Û S cos(! z t ' 1 ) für ! 0 > ! 1 (4) 

2 

bzw. 

u ZF (t) = A 1 Û 0 Û S cos(! z t + ' 1 ) für ! 0 < ! 1 (5) 

2 

A ist dabei eine charakteristische Konstante des Multiplizierers. u ZF (t) gibt dabei sowohl die Amplitude 

Û S als auch die Phase ' 1 des Eingangssignals wieder, wobei die Phase für ! 0 < ! 1 in Gleichlage und 

für ! 0 > ! 1 in Kehrlage wiedergegeben wird. 



Wir unterscheiden damit zwischen Gleichlage- und Kehrlage-Mischern. Weiterhin unterscheiden wir 

zwischen Aufwärts- und Abwärtsmischern, je nachdem ob ! z gröÿer oder kleiner als ! 1 ist. Wir kommen 

damit zu folgenden Mischprinzipien: 

1. ! 0 < ! 1 : 

a) ! z = ! 1 ! 0 : Abwärtsmischer in Gleichlage 

b) ! z = ! 1 + ! 0 : Aufwärtsmischer in Gleichlage 

2. ! 0 > ! 1 : 

a) ! z = ! 0 ! 1 : Abwärtsmischer in Kehrlage (für ! z < ! 1 , sonst Aufwärtsmischer) 

b) ! z = ! 0 + ! 1 : Aufwärtsmischer in Gleichlage 

Die obigen Betrachtungen lassen sich auch auf nicht-harmonische Signale u s (t) verallgemeinern, wobei 

u s (t) durch seine Fouriertransformierte U S (j!) dargestellt wird: 

u s (t) ❞ US (j!) (6) 

Mit einem Lokaloszillator-Signal 

u 0 (t) = 2 cos(! 0 t) (7) 

gilt dann 

u s (t) ¡ u 0 (t) = U S 

( 

j(! !0 ) ) + U S 

( 

j(! + !0 ) ) : (8) 

Das Eingangsignal wird damit um die Frequenz ! 0 sowohl nach oben als auch nach unten verschoben, 

es bleibt aber ansonsten unverändert, so dass keine Informationen verloren gehen. 

Für einen Abwärtsmischer in Kehrlage entsprechend 2a) in obiger Darstellung (! 0 > ! 1 , ! z = ! 0 ! 1 ) 

ergibt sich das Spektrum in Abb. 2. Als Ausgangssignal werden die Spektralkomponenten um ! z = 

! 0 ! 1 herum herausgeltert. 

U S (j(ω + ω 0)) U S (jω) 

U S (j(ω − ω 0)) 

−(ω 0 + ω 1) −ω 0 −ω 1 −(ω 0 − ω 1) +(ω 0 − ω 1) +ω 1 +ω 0 

+(ω 0 + ω 1) 

Abb. 2: Eingangs- und Ausgangsspektrum für einen Kehrlage-Abwärtsmischer. 

1.1 Spiegelfrequenz 

Wenn wir einen Kehrlage-Abwärtsmischer voraussetzen mit einer festen (durch die Wahl des Filters am 

Ausgang festgelegten) Zwischenfrequenz ! z , liegt die gewünschte Eingangsfrequenz bei ! 1 = ! 0 ! z . 

Es ist allerdings zu beachten, dass dann auch (unerwünscht) ein Eingangssignal bei der Frequenz 



! 0 1 = ! 0 + ! z auf die gleiche Zwischenfrequenz ! z umgesetzt wird. ! 0 1 

wird als Spiegelfrequenz 

bezeichnet, und der Abstand zwischen Soll-Eingangsfrequenz und Spiegelfrequenz ist durch 

! 0 1 

! 1 = 2! z ; (9) 

also die doppelte Zwischenfrequenz gegeben. 

Um damit ein eindeutiges Zwischenfrequenzsignal zu ermöglichen, muss die Spiegelfrequenz am Eingang 

durch entsprechende Filterung unterdrückt werden. 

Es ist damit ein Kompromiss zu nden zwischen einer einfachen Filterrealisierung am Eingang (möglichst 

hohe Zwischenfrequenz) und einer unproblematischen Signalverarbeitung (möglichst niedrige 

Zwischenfrequenz). Gegebenenfalls können auch mehrere Mischstufen hintereinander geschaltet werden 

(zunächst hohe Zwischenfrequenz und am Ausgang niedrige Zwischenfrequenz). 

2 Realisierung von Mischern mit nichtlinearen Kennlinien 

Die Multiplikation auch bei hohen Frequenzen lässt sich durch nichtlineare Kennlinien realisieren. Beispielsweise 

eignen sich dazu nichtlineare Kennlinien zwischen Strom und Spannung bei Dioden und 

Transistoren. 

Abb. 3: Strom und Spannung bei Dioden und Transistoren. 

Der Zusammenhang zwischen dem Strom i (t) und der Spannung u(t) ist dabei durch 

i = f (u) (10) 

gegeben mit der nichtlinearen Funktion f (u). Zur Vereinfachung wollen wir hier annehmen, dass der 

Strom i instantan der Spannung u folgt und Ladungsspeichereekte vernachlässigt werden können. 

2.1 Hochfrequenzgleichrichtung 

Bevor wir uns dem eigentlichen Mischer zuwenden, wollen wir eine nichtlineare Kennlinie i = f (u) 

betrachten, die nur von einem harmonischen Signal 

u(t) = U g + Û cos(!t): (11) 

ausgesteuert wird. 

Es sei 

i (t) = f (u(t)) = I S 

⎡ 

( ) 

u(t) 

⎣ exp 

U T 

1 

⎤ 

⎦ (12) 



Abb. 4: Beispielhafter Verlauf von u(t) und i (t) bei einer Diodenkennlinie (hier mit Û = U T 

U g = 0; 6U T ). 

und 

mit dem Sperrstrom I S und der Temperaturspannung U T = kT e 

(U T = 26 mV bei Raumtemperatur 

T = 290 K). Im Abb. 4 ist der Verlauf zwischen u(t) und i (t) beispielhaft skizziert. 

Der Strom i (t) ist dann immer noch periodisch mit der Periodendauer = 2 ! 

, so dass dann i (t) als 

Fourierreihe geschrieben werden kann: 

mit den Fourierkozienten 

A m = 1 

+=2 ∫ 

=2 

i (t) = 

i (t) exp( jm!t) dt = 1 

+1 ∑ 

m= 1 

+=2 ∫ 

=2 

A m exp(jm!t) (13) 

⎛ [ 

Ug + 

I S 

⎝ Û 

] 

cos(!t) 

exp 

U T 

1 

⎞ 

⎠ exp( jm!t) dt (14) 

Zur Lösung von Gl. (14) wird die modizierte Besselfunktion I m (x ) der Ordnung m eingeführt: 

so dass sich aus Gl. (14) ergibt: 

A m = I S exp 

I m (x ) = 1 

2 

( 

Ug 

U T 

) 

∫ 

+ 

 

I m 

( Û 

U T 

) 

⎡ ( ) ( ) 

Ug 

A 0 = I S 

⎣ Û 

exp I 0 

U T U T 

exp(x cos y ) cos(my ) dy; (15) 

1 

⎤ 

für m 6= 0 (16) 

⎦ für m = 0 (17) 

In Abb. 5 sind modizierte Besselfunktionen beispielhaft dargestellt. 

Solange die Diodenkennlinie nur schwach ausgesteuert wird ( Û U T ), ergibt sich auch für den Strom 

ein nahezu harmonischer Verlauf, wobei die Verzerrungen durch die Fourierkoezienten A m mit m 2 

charakterisiert werden. Gelegentlich wird auch ein Klirrfaktor eingeführt, wobei der Klirrfaktor der 

Ordnung m gegeben ist als 

A m 

k m = 

∣ 

A 1 

∣ ∣∣∣∣ 

: (18) 



I m 

I 0 

I 1 

I 2 

I 3 

Abb. 5: Modizierte Besselfunktionen I m (x ) der Ordnung m = 0 : : : 3. 

x 

Zur einfacheren Analyse von A m ist es zweckmäÿig, Näherungen für I m (x ) für kleine und groÿe Argumente 

von x einzuführen. So gilt für x 1: 

I m (x ) 1 m! 

( x 

2 

) m 

für m 6= 0 (19) 

I 0 (x ) 1 + x 2 

während für x 1 sich alle I m (x ) dem Grenzwert 

2 

für m = 0 (20) 

nähern. 

I m (x ) exp(x p 

) 

2x 

(21) 

Beispiel: 

Als Beispiel werde die Gleichrichterschaltung in Abb. 6 betrachtet. Die Kapazität C sei sehr 

groÿ, so dass an ihr nur die Gleichspannung U g abfällt. U g hängt zusammen mit dem Gleichstrom 

von i (t), der sich mit Gl. (13) zu A 0 ergibt. Damit gilt 

U g = A 0 ¡ R (22) 

und damit ergibt sich mit Gl. (17) 

U g = I S ¡ R 

⎡ 

⎣ exp 

( 

Ug 

U T 

) 

I 0 

( Û 

U T 

) 

1 

⎤ 

⎦ ; (23) 

woraus sich die Gleichrichtspannung U g als Funktion der Hochfrequenz-Wechselspannung Û 

bestimmen lässt. Für Û U T folgt aus Gl. (23) mit Gl. (20): 

U g = 

⎛ 

Û 2 

⎝ 1 

U T 2 + U T 

I S ¡R 

⎞ 

⎠ ; (24) 



so dass man dann auch von einer quadratischen Gleichrichtung spricht. Für Û U T folgt aus 

Gl. (23) mit Gl. (21): 

U g = Û; (25) 

so dass man dann von linearer Hochfrequenz-Gleichrichtung spricht. 

Abb. 6: Schaltung zur Hochfrequenzgleichrichtung. 

2.2 Mischer mit nichtlinearer Transistorkennlinie 

Wir betrachten entsprechend Abb. 3 einen Transistor, der mit einer Überlagerung aus Signal- und 

Lokaloszillator-Spannung ausgesteuert wird. Es gilt damit für u(t): 

Für das Lokaloszillator-Signal gilt 

u(t) = u s (t) + u 0 (t): (26) 

u 0 (t) = U g + Û 0 cos(! 0 t): (27) 

Weiterhin soll der Transistor durch das Eingangssignal u s (t) nur schwach ausgesteuert werden, so dass 

gilt. Diese Aussteuerung ist in Abb. 7 skizziert. Es gilt 

i (t) = f (u(t)) = f (u 0 (t) + u s (t)) = f (u 0 (t)) + u s (t) 

ju s (t)j Û 0 : (28) 

df (u) 

du 

∣ 

∣ 

u=u0 (t) 

+ : : : (29) 

Gl. (29) stellt die Taylor-Entwicklung von f (u) um u 0 (t) herum dar, wobei nur das erste Glied der 

df (u) 

Taylor-Entwicklung dargestellt ist. 

du j u=u 0 (t) stellt die durch das Lokaloszillator-Signal gesteuerte 

zeitabhängige Steilheit des Transistors dar. Diese Steilheit ändert sich periodisch entsprechend 

der Frequenz des Lokaloszillators und wird mit dem Eingangssignal multipliziert. Diese Multiplikation 

df (u) 

führt zu der gewünschten Frequenzumsetzung. Die Steilheit S(t) = 

du 

j u=u 0 (t) lässt sich wieder als 

Fourierreihe darstellen: 

S(t) = 

df (u) 

du 

∣ 

∣ 

u=u0 (t) 

= 

+1 ∑ 

m= 1 

Y m exp(jm! 0 t) (30) 



i = f (u) 

Steigung 

( ) df 

du 

U g 

u s (t) 

u 

u 0 (t) 

Zeit t 

Abb. 7: Die Kennlinie i = f (u) wird von u s (t) und u 0 (t) ausgesteuert, wobei die Kennlinie im Bereich 

der Aussteuerung von u s (t) im Wesentlichen linear ist. Da der Parameter df durch du u 0(t) gesteuert 

wird, spricht man auch von einer parametrischen Schaltung. 



Beispiel: 

Beim bipolaren Transistor gilt für den Zusammenhang zwischen Strom und Spannung die 

Diodenkennlinie von Gl. (6), so dass für die Ableitung 

df 

I ( ) 

S u0 (t) 

du 

∣ = exp 

(31) 

U T U T 

∣ 

u0 (t) 

gilt. Für u 0 (t) entsprechend Gl. (27) ergeben sich die Fourierkoezienten Y m 

zu: 

Y m = 1 

+=2 ∫ 

=2 

I S 

U T 

exp 

( ) 

u0 (t) 

exp( jm! 0 t) dt (32) 

U T 

Y I ( ) ( ) 

S Ug Û0 

m = exp I m 

U T U T U T 

wieder mit der modizierten Besselfunktion I m (x ). 

(33) 

Das gesamte Spektrum des Stroms i (t) gemäÿ Gl. (10) ergibt sich mit Gl. (30) und u s (t) = 

1=2[U S exp(j! 1 t) + c:c:] zu: 

i (t) = f (u 0 (t)) + 1 2 

+1 ∑ 

m= 1 

[ 

US ¡ Y m exp(j(m! 0 + ! 1 )t) + U £ S ¡ Y m exp(j(m! 0 ! 1 )t) ] (34) 

Der erste Term f (u 0 (t)) beinhaltet ähnlich zu Gl. (6) die Harmonischen des Lokaloszillator-Signals 

m ¡ ! 0 , während im zweiten Term die Mischprodukte (m! 0 + ! 1 , m! 0 ! 1 ) erscheinen. 

Wenn wir als Beispiel einen Kehrlage-Abwärtsmischer betrachten (! 0 > ! 1 , ! z = ! 0 ! 1 ), ergibt 

sich das Zwischenfrequenzsignal bei ! z aus Gl. (34) zu: 

i ZF (t) = 1 2 

[ 

Y 1 U £ S exp(j(! 0 ! 1 )t) + Y £ 1 U S exp( j(! 0 ! 1 )t) ] ; (35) 

wobei wir von Y 1 = Y £ 1 

Gebrauch gemacht haben. 

Das Zwischenfrequenzsignal lässt sich damit durch einen Zeiger 

I ZF = Y 1 ¡ U £ S (36) 

darstellen, wobei Y 1 die Übertragung von der Signalspannung zum Zwischenfrequenzstrom beschreibt. 

Y 1 wird deshalb auch als Mischsteilheit bezeichnet. 

Im obigen Beispiel haben wir die Umsetzung eines Eingangssignals bei der Frequenz ! 1 auf die Zwischenfrequenz 

(! 0 ! 1 ) beschrieben. Wir sprechen dann von einem Grundwellenmischer. 

Es lassen sich aber auch die Oberwellen von ! 0 ausnutzen, indem man die Eingangsfrequenz ! 1 auf 

die Zwischenfrequenz (m ¡ ! 0 ! 1 ) umsetzt. Man spricht dann von einem Oberwellenmischer mit der 

Mischsteilheit Y m . Die Ezienz eines Oberwellenmischers ist geringer als die eines Grundwellenmischers; 

dafür genügt aber die Realisierung eines Lokaloszillators bei einer um den Faktor m niedrigeren 

Frequenz. 



Abb. 8: Prinzipieller Aufbau eines Heterodyn-Empfängers. 

3 Beispiele für die Realisierung von Mischern 

Ein typisches Beispiel für einen Mischer ist ein Heterodyn-Empfänger, wie er in Abb. 8 dargestellt 

ist. 

Er besteht aus einem Vorverstärker mit einem Filter zu Unterdrückung der Spiegelfrequenz. Das Eingangssignal 

wird mit einem Mischer auf eine feste Zwischenfrequenz umgesetzt, die dann ein ZF-Filter 

passiert, bevor es der Demodulation bzw. der weiteren Signalverarbeitung zugeführt wird. Die Frequenz 

des Lokaloszillators (variabel) wird dabei so eingestellt, dass die gewünschte Eingangsfrequenz korrekt 

auf die feste voreingestellte Zwischenfrequenz umgesetzt wird. 

Beispiele dafür stellen Rundfunkempfänger dar, wobei in Abb. 9 beispielhaft ein FM-Tuner (UKW- 

Empfänger) dargestellt ist. Es handelt sich dabei um eine ältere Schaltungsrealisierung (ca. 1970), die 

mit einer geringen Zahl von diskreten Bauelementen die in Abb. 8 genannten Funktionen, Vorverstärker, 

Spiegelfrequenzlter, Mischer, Lokaloszillator und ZF-Filter realisiert. 

Wir haben dort einen FET-Vorverstärker mit eingangs- und ausgangsseitigem Filter (abstimmbar zur 

Unterdrückung der jeweiligen Spiegelfrequenz). Der untere Teil der Schaltung stellt einen Colpitts- 

Oszillator dar (vgl. Abb. 17 in Abschnitt RÜ) ,und die Mischstufe wird durch einen Bipolartransistor 

dargestellt, an den sich am Ausgang ein Filter bei der Zwischenfrequenz um 10,7 MHz anschlieÿt. 

Neben den oben dargestellten Mischern mit Transistoren lassen sich auch Mischer mit nichtlinearen 

Kennlinien anderer Bauelemente realisieren. Jenseits der Grenzfrequenz von Transistoren lassen 

sich beispielsweise Schottky-Dioden (vgl. Skript Hochfrequenztechnik I) einsetzen, da diese eine sehr 

schnelle Steuerung des dierentiellen Widerstands ermöglichen (einsetzbar bis Frequenzen im Bereich 

von 1000 GHz), wie weiter unten genauer erläutert wird. 

Der Frequenzbereich von ca. 1100 THz (1 THz=10 12 Hz) ist technisch nur schwer zugänglich, während 

Mischer im optischen Frequenzbereich oberhalb von ca. 100 THz ( 0 3 m) wieder sehr einfach 

mit Hilfe von Fotodioden realisiert werden können. Das Prinzip einer Mischung im optischen Frequenzbereich 

ist in Abb.10 skizziert. 

Das Feld des Eingangssignals E s (t) (bei der optischen Frequenz ! 1 ) wird mit dem Feld des Lokaloszillatorsignals 

E 0 (t) bei der Frequenz ! 0 überlagert, so dass sich an der Fotodiode ein Feld 

E(t) = E 0 (t) + E s (t) (37) 

ergibt. Der Fotostrom i (t) ist proportional zur einfallenden optischen Leistung und damit proportional 



Abb. 9: Realisierungsbeispiel für einen FM-Tuner mit diskreten Bauelementen. 

Abb. 10: Prinzip eines Mischers von zwei optischen Signalen mit einer Fotodiode. 



zu E 2 (t), so dass sich ergibt: 

i (t) / E 2 (t) = E 2 0 + E2 s + 2E 0(t)E s (t) (38) 

Der Mischterm in Gl. (38) wird durch E 0 (t)E s (t) repräsentiert, wobei bei dieser Multiplikation die 

gewünschte Zwischenfrequenz ! z = j! 0 ! 1 j entsteht. Dieses Prinzip wird in der kohärenten optischen 

Nachrichtentechnik angewandt. 

4 Mischer mit Schottky-Dioden 

Die Schottky-Diode wird wieder durch eine Dioden-Kennlinie i = f (u) entsprechend Gl. (12) charakterisiert, 

wobei der Einuss von parasitäten Kapazitäten sehr gering ist. 

Die Schottky-Diode wird nur mit einer Überlagerung von Lokaloszillator, Eingangssignal und Zwischenfrequenzsignal 

ausgesteuert, wobei diese drei Signale in irgendeiner Weise an die Schottky-Diode 

herangeführt werden müssen. Um die im Allgemeinen recht komplizierte Analyse handhabbar zu machen, 

wollen wir hier als Beispiel eine ideale Spannungseinprägung voraussetzen. 

An der Schottky-Diode liegt dann die Summenspannung aus der Lokaloszillator-Spannung u 0 (t), der 

Eingangssignal-Spannung u s (t) und der ZF-Signal-Spannung u ZF (t) an. 

ω 0 

ω 1 

ω z =(ω 1 − ω 0 ) 

Abb. 11: Schematische Anordnung eines Mischers mit einer Schottky-Diode und 

Spannungseinprägung. 

Das Prinzip einer solchen Spannungseinprägung ist in Abb. 11 skizziert. Die in Abb. 11 eingezeichneten 

Schwingkreise sind symbolisch so zu verstehen, dass sie für alle anderen Frequenzen als die jeweilige 

Soll-Frequenz Kurzschlüsse darstellen. Wie in Abb. 7 wird die Diodenkennlinie im Wesentlichen durch 

das Lokaloszillator-Signal u 0 (t) ausgesteuert, während sie durch u s (t), u ZF (t) nur im linearen Bereich 



betrieben wird. Der Strom durch die Schottky-Diode i (t) ergibt sich dann ähnlich wie in Gl. (29) zu 

i (t) = f (u(t)) = f [u 0 (t)) + u s (t) + u ZF (t)] = f (u 0 (t)) + [u s (t) + u ZF (t)] df 

∣ ; (39) 

du 

∣ 

u0 (t) 

wobei sich df 

du j u 0 (t) als ein zeitabhängiger Leitwert g(t) auassen lässt, der sich periodisch mit der 

Periode = 2=! 0 wieder wie in Gl. (20) als Fourierreihe entwickeln lässt: 

df 

+1 ∑ 

g(t) = du 

= 

∣ m= u0 

1 

(t) 

Y m exp(jm! 0 t); (40) 

wobei Y m = Y £ m für alle reellen g(t) gelten muss. 

Die Mischung mit der Schottky-Diode erfolgt also im Wesentlichen dadurch, dass durch Aussteuerung 

der Schottky-Diode mit u 0 (t) ein zeitabhängiger dierentieller Leitwert g(t) entsteht. 

Damit entspricht Abb. 11 der Anordnung in Abb. 12. 

Signalkreis 

ZF-Kreis 

ω 1 ω z =(ω 1 − ω 0 ) 

Abb. 12: Mischung mit einem sich periodisch verändernden Leitwert g(t) (resistiver Mischer) und 

Spannungseinprägung. 

Aus Abb. 12 folgt 

i (t) = [ u s (t) + u ZF (t) ] g(t); (41) 

was genau Gl. (39) entspricht (ohne den für die Mischung unerheblichen Term f [u 0 (t)]). Das g(t) in 

Abb. 12 muss nicht unbedingt mit einer Schottky-Diode realisiert werden, möglich ist z. B. auch die 

Steuerung des Kanalleitwerts eines FETs durch die Gate-Source-Spannung. 

Für einen Gleichlage-Abwärtsmischer (! 1 > ! 0 , ! z = ! 1 ! 0 ) führt Gl. (41) mit 

und g(t) gemäÿ Gl. (40) auf 

i (t) = 1 2 

u s (t) = 1 2 

u ZF (t) = 1 2 

[ 

US exp(j! 1 t) + c:c: ] (42) 

[ 

UZF exp(j(! 1 ! 0 )t) + c:c: ] (43) 

[ 

US exp(j! 1 t) + U ZF exp(j(! 1 ! 0 )t) + c:c: ] +1 ∑ 

m= 1 

Y m exp(jm! 0 t) (44) 

Gl. (44) führt auf unendlich viele Frequenzkomponenten j! 1 ¦ m! 0 j, wovon für den Mischvorgang 

in Abb. 12 nur die Frequenzkomponenten bei ! 1 und ! z = (! 1 ! 0 ) interessieren, da alle anderen 

Frequenzkomponenten im Rahmen des Ansatzes der Spannungseinprägung kurzgeschlossen werden. 

Aus Gl. (44) folgt für die Stromkomponenten bei ! 1 und (! 1 ! 0 ) (Y 1 = Y £ 1; Y = Y 0 reell) 

i (t) = 1 2 

[ 

(US ¡ Y 0 + U ZF ¡ Y 1 ) exp(j! 1 t) + (U ZF Y 0 + U S ¡ Y £ 1 ) exp(j(! 1 ! 0 )t) + c:c: ] ; (45) 



wobei für die Ströme bei der Signalfrequenz und Zwischenfrequenz wieder Stromzeiger eingeführt 

werden können: 

so dass sich aus Gl. (45) ergibt: 

i s (t) = 1 2 

i ZF = 1 2 

[ 

IS exp(j! 1 t) + c:c: ] ; (46) 

[ 

IZF exp(j(! 1 ! 0 )t) + c:c: ] ; (47) 

I S = (U S ¡ Y 0 + U ZF ¡ Y 1 ) (48) 

I ZF = (U ZF ¡ Y 0 + U S ¡ Y £ 1 ) (49) 

Gl. (48) und (49) lassen sich in Matrix-Schreibweise formulieren: 

⎛ ⎞ ⎛ ⎞ ⎛ ⎞ 

⎝ I S ⎠ = ⎝ Y 0 Y 1 

⎠ ⎝ U S ⎠ (50) 

I ZF Y 0 U ZF 

Y £ 1 

Gl. (50) entspricht formal der Beschreibung mit y-Parametern gemäÿ Abb. 13. Das Netzwerk entsprechend 

Abb. 12 und 13 ist ja auch ein lineares Netzwerk, aber es ist nicht zeitinvariant, weshalb 

die Zeiger I S , U S bzw. I ZF , U ZF auf jeweils unterschiedliche Frequenzen bezogen sind. 

I S 

U S 

(Y ) 

I ZF 

U ZF 

Abb. 13: Mischer als lineares Umsetzungsnetzwerk. 

Interessant ist nun der maximal erreichbare Konversionswirkungsgrad von der Signalfrequenz ! 1 zu 

der Zwischenfrequenz ! ZF = ! 1 ! 0 . Dazu kann die aus den y-Parametern bekannte maximale 

Leistungsverstärkung Gm 0 herangezogen werden. Aus Gl. (RÜ 27) mit Gl. (RÜ 26) folgt: 

G 0 jy 

m = 21 

j 2 

(51) 

2


Die maximale Leistungsverstärkung Gm 0 nähert sich 1 für Y 1 

Y 0 

! 1, was für Û 0 

U T 

! 1 erreicht wird. Für 

ein noch realistisches Û 0 

U 

= 10 

T 

ergibt sich beispielsweise ein Gm 0 = 0; 5 ( 3 dB), was trotz der hier 

durchgeführten Näherungen (ideale Spannungseinprägung) ein realistisches Ergebnis darstellt. 

Dieses maximale 

√ 

Gm 0 wird erreicht, wenn sowohl auf der Signal- als auch auf der ZF-Seite an den 

Leitwert Y = Y 2 Y 2 

0 1 

angepasst wird. 

Die Rauschzahl eines derartigen realistischen Mischers ist ähnlich wie bei einem passiven Netzwerk 

F 1 

Gm 

0 ; (54) 

wenn G 0 m die verfügbare Konversionsezienz des Mischers (G m < 1) bezeichnet. 

5 Gegentaktmischer 

Der Nachteil des Mischers mit Schottky-Dioden, wie wir ihn in Abschnitt 4 diskutiert haben, besteht 

darin, dass neben dem gewünschten Produkt 

[u s (t) + u ZF (t)] ¡ g(t) 

mit g(t) = df 

du j u 0 (t) in Gl. (39) mit dem Term f (u 0 (t)) noch die Harmonischen von ! 0 erscheinen. Zur 

Vermeidung dieses Terms werden Schottky-Dioden-Mischer häug als sogenannte Gegentaktmischer 

aufgebaut. 

Das Prinzip eines Gegentaktmischers zeigt Abb. 14. 

Abb. 14: Prinzip eines Gegentaktmischers mit u 1 (t) = u 0 (t)+u s (t)+u ZF (t) und u 2 = u 0 (t) u s (t) 

u ZF (t). 

Wir gehen dabei von zwei gleichen Schottky-Dioden aus, die jeweils mit der Spannung 

und 

u 1 = u 0 (t) + u s (t) + u ZF (t) (55) 

u 2 = u 0 (t) u s (t) u ZF (t) (56) 

ausgesteuert werden. Der Dierenzstrom i (t) = i 1 (t) i 2 (t) ergibt sich als 

i (t) = f (u 1 (t)) f (u 2 (t)) 

= 2[u s (t) + u ZF (t)]g(t) (57) 



mit g(t) entsprechend Gl. (40), so das man dann wieder die Multiplikation wie in Gl. (41) erhält. 

Ein solcher Mischer lässt sich aufbauen mit einem 3 dB -Koppler, 

180 180 -Hybrid oder Magisches T (vergleiche 

Hochfrequenztechnik I, Abschn. HS), der z. B. als Ringkoppler (HFT I, Abschn. HS, Abb. 13) 

realisiert werden kann. Ein Realisierungsbeispiel zeigt Abb. 15. 

Abb. 15: Gegentaktmischer mit Ringkoppler und zwei Schottky-Dioden. 

Die Kapazität C in Abb. 15 soll einen Tiefpass repräsentieren, der für das hochfrequente Signal und 

den Lokaloszillator einen Kurzschluss und das ZF-Signal einen Leerlauf darstellt. An den Schottky- 

Dioden liegt jeweils die Summe bzw. die Dierenz von Lokaloszillator- und Eingangssignal an, während 

sich der Strom des ZF-Signals gleichzeitig auf die beiden Schottky-Dioden aufteilt. 

6 Ringmischer 

Ein Nachteil des oben diskutierten Gegentaktmischers besteht noch darin, dass g(t) immer positiv ist 

und damit der Gleichanteil Y 0 von g(t) in Gl. (40) nicht verschwindet. Die führt dazu, dass der Strom 

i (t) in Abb. 14 und 15 oder Gl. (41) immer auch Spektralanteile des Eingangssignals mit beinhaltet. 

Idealerweise wäre bei g(t) in Gl. (40) Y 0 = 0 und nur Y 1 = Y £ 1 6= 0. Um einem solchen idealen 

Verhalten näher zu kommen, verwendet man einen sogenannten Ringmischer, wie er in Abb. 16 

schematisch dargestellt ist. 

Für u 0 (t) > 0 werden die Dioden D 2 und D 4 leitend (im Idealfall Kurzschluss), während D 1 und D 3 

sperren (im Idealfall Leerlauf). Für u 0 (t) < 0 drehen sich die Verhältnisse um. 

Dann lässt sich idealerweise schreiben: 

u ZF = u s (t) ¡ s(t) (58) 

mit der Schaltfunktion 

⎧ 

⎪⎨ 

s(t) = 

⎪⎩ 

+1 für u 0 (t) > 0 

1 für u 0 (t) < 0 

(59) 

Diese Multiplikation in Gl. (58) kommt der idealen Multiplikation für einen Mischer in Gl. (3) sehr 

nahe und ist auch einmal in Abb. 17 skizziert. 



ZF 

Abb. 16: Prinzip eines Ringmischers bzw. Ringmodulators. 

s(t) 

+1 

u ZF (t) 

u s (t) 

−1 

Abb. 17: Schematische Darstellung der Multiplikation von u s (t) mit s(t) bei einem Ringmischer. 



Das Prinzip eines Ringmischers ist nicht auf die Realisierung mit Dioden beschränkt. Eine Realisierung 

mit Feldeekttransistoren führt auf den sogenannten Gilbert-Mischer in Abb. 18. Das (dierentielle) 

Eingangssignal wird dabei zwischen den Anschlüssen RF und RF + angelegt, während das 

ZF-Ausgangssignal sich als dierentielles Ausgangssignal zwischen den Knoten 1 und 2 ergibt. Der 

Lokaloszillator wird zwischen LO und LO + angeschlossen. 

– 

Abb. 18: Prinzip eines Gilbert-Mischers. 

Die Äquivalenz zu einem Ringmischer wird deutlich, wenn man Abb. 18 etwas umzeichnet, woraus sich 

Abb. 19 ergibt. 

Zwischen- 

Frequenz- 

Ausgang 

Eingangssignal 

Abb. 19: Gilbert-Mischer, dargestellt in Form eines Ringes. 

7 Parametrische Frequenzumsetzung mit gesteuerter Kapazität 

Wir haben oben die Mischung mit einem steuerbaren Leitwert g(t) diskutiert. Es stellt sich hier die 

Frage, ob nicht auch die Mischung mit einer steuerbaren Kapazität c(t) möglich wäre. Auf den esten 



Blick hätte eine gesteuerte Kapazität den Vorteil, dass keine Verluste entstehen. 

Allgemein lässt sich eine nichtlineare Kapazität durch eine nichtlineare Beziehung zwischen der Ladung 

q(t) und der Spannung u(t) entsprechend 

q(t) = h[u(t)] (60) 

beschreiben, woraus sich die dierentielle Kapazität 

dq 

c(t) = du 

∣ 

u0 (t) 

(61) 

ergibt, wobei die nichtlineare Kapazität durch die Lokaloszillator-Spannung u 0 (t) ausgesteuert wird. 

c(t) lässt sich dann wie in Gl. (40) als Fourier-Reihe schreiben: 

c(t) = 

m=+1 

∑ 

m= 1 

C m exp(jm! 0 t) (62) 

mit reellem C 0 = C 0 und C m = C£ m. In Abb. 12 lässt sich dann g(t) durch c(t) und der Strom i (t) 

durch die Ladung q(t) ersetzen, woraus dann statt Gl. (41) für q(t) folgt: 

q(t) = [u s (t) + u ZF (t)]c(t) (63) 

Statt für den Strom schreiben wir jetzt für die Ladung bei dem Eingangs- bzw. Zwischenfrequenzsignal 

(vgl. Gl. (46), (47)) 

q s (t) = 1 2 [Q S exp(j! 1t) + c:c:] (64) 

q ZF (t) = 1 2 [Q ZF exp(j(! 0 ! 1 )t) + c:c:]; (65) 

woraus sich dann wie in Gl. (50) in Matrix-Schreibweise ergibt: 

⎛ ⎞ ⎛ ⎞ ⎛ ⎞ 

⎝ Q S ⎠ = ⎝ C 0 C 1 

⎠ ⎝ U S ⎠ : (66) 

Q ZF 

C 0 U ZF 

C £ 1 

Wenn man jetzt versucht, den Konversionswirkungsgrad zu ermitteln, muss man von der Ladung q(t) 

zum Strom i (t) = dq(t) 

dt 

übergehen, woraus 

I S = j! 1 Q S 

und I ZF = j! ZF Q ZF 

(67) 

folgt. Hier wird das Problem eines Abwärtsmischers mit gesteuerter Kapazität deutlich: Für ! ZF ! 1 

ergeben sich bei der Zwischenfrequenz sehr kleine Ströme (und damit auch sehr kleine Leistungen), 

so dass ein Abwärtsmischer mit gesteuerter Kapazität nicht vernünftig realisiert werden kann. Anders 

verhält es sich jedoch bei einem Aufwärtsmischer (! ZF ! 1 ); hier ist sogar eine Verstärkung möglich 

(parametrische Verstärkung). 

Für gesteuerte Kapazitäten gibt es allgemeine Gesetzmäÿigkeiten für die Leistungsbeziehungen (Manley- 

Rowe-Gleichungen), die hier aber nicht weiter diskutiert werden sollen. 


Hochfrequenztechnik II Modulationsverfahren MOD/1 

1 Analoge und digitale Signale 

Modulationsverfahren werden benötigt, um ein vorhandenes Basisbandsignal s(t) über ein hochfrequentes 

Trägersignal zu übertragen. Dieses Signal kann vorliegen als analoges Signal s(t) mit der 

Bandbreite ∆f . Wir sprechen dann auch von einem zeit- und wert-kontinuierlichem Signal. s(t) kann 

aber auch vorliegen als ein wert- und zeit-diskretes Signal, wobei wir dann von einem digitalen Signal 

s(t) sprechen. 

1.1 Digitale Signale 

Zur Gewinnung dieses digitalen Signales wird das Ursprungssignal mit einer festen Abtastrate f B abgetastet, 

und nur die Signalwerte zu diesen festen Abtastzeitpunkten werden übertragen (zeitdiskrete 

Übertragung). Das analoge Ursprungssignal ist ohne jeglichen Verlust aus den zeitdiskreten Abtastwerten 

wieder gewinnbar, wenn für die Abtastrate 

f B > 2∆f a (1) 

gilt (mit der Bandbreite ∆f a des analogen Ursprungssignals). Bei einem digitalen Signal werden diese 

einzelnen Abtastwerte quantisiert übertragen. (wertdiskrete Übertragung), z. B. mit 2 n Quantisierungsstufen, 

wobei n die Anzahl der „bits” pro Abtastzeitpunkt beschreibt. Die benötigte Bitrate für 

das digitale Signal ist dann durch 

gegeben. 

Beispiel: 

B = n · f B > 2n · ∆f a (2) 

Wenn man von einem analogen Ursprungssignal mit ∆f = 5 MHz Bandbreite ausgeht, das 

mit n = 8, also 2 n = 256 Quantisierungsstufen, übertragen werden soll, benötigt man eine 

Bitrate von mindestens 

B > 2 · 8 · 5 Mbit 

s 

= 80 Mbit 

s 

Bei z. B. einem Videosignal lässt sich die Datenrate jedoch mit entsprechender Quellenkodierung, 

z. B. MPEG, erheblich reduzieren. 

Wenn ein digitales Signal mit der Bitrate B als binäres NRZ-Signal (NRZ – non-return-to-zero) 

übertragen werden soll, muss der Übertragungskanal die Bandbreite 

∆f = B 2 

(3) 

bereitstellen, wie am Beispiel von Abb. 1 deutlich wird. 

Man kann das NRZ-Signal in Abb. 1 auffassen als die Übertragung von B Symbolen pro Sekunde, 

wobei jedes Symbol die Information von „1 bit” beinhaltet. Pro Symbol können in höherwertigen 

Modulationsverfahren auch mehr Informationen übertragen werden, z. B. m-bits (d. h. z. B. pro Symbol 

2 m diskrete Amplitudenwerte), so dass sich dann die Symbolrate S zu 

S = B m 



s(t) 

1 0 1 0 1 0 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 1 

max. Frequenzkomponente B 2 

Abb. 1: Binäres NRZ-Signal und die darin enthaltene maximale Frequenzkomponente B 2 . 

t 

ergibt, und die erforderliche Bandbreite für dieses mehrstufige digitale Signal ist dann entsprechend zu 

Gl. (3) als 

gegeben. 

∆f = S 2 = B 

2m 

(4) 

2 Trägermodulationsverfahren 

Das eben diskutierte Signal s(t) soll nun mit einer Trägerfrequenz f T (bzw. ω T = 2π · f T ) in der 

Hochfrequenz-Ebene übertragen werden. Das hochfrequente modulierte Signal u M (t) kann dann geschrieben 

werden als: 

u M (t) = Û M (t) cos[ω T t + ϕ(t)] = R[u(t) exp(jω T t)] (5) 

mit dem komplexen (jetzt zeitabhängigen) Zeiger u(t) 

u(t) = Û M (t) exp[jϕ(t)]. (6) 

Wir wollen ein reelles Eingangssignal s(t) mit |s(t)| ≤ 1 voraussetzen, wobei der Zeiger u(t) dem 

Eingangssignal s(t) in geeigneter Weise folgt. s(t) kann dabei sowohl als analoges als auch als digitales 

Signal vorliegen. 

Wie Gl. (6) zeigt, kann man u(t) bezüglich der Amplitude, der Phase oder der Frequenz modulieren. 

Wir wollen im Folgenden diese verschiedenen Modulationsarten diskutieren. 

Amplitudenmodulation: Bei einer reinen Amplitudenmodulation wird in Gl. (6) nur die Amplitude 

Û M (t) moduliert und die Phase ϕ(t) bleibt konstant (z. B. ϕ(t) = 0). Der zeitabhängige Zeiger 

u(t) ist dann rein reell, und es gilt 

u(t) = Û M0 [1 + m · s(t)] (7) 

mit der mittleren Amplitude Û M0 und dem Modulationsindex m mit m ≤ 1. Durch die Bedingung 

(m ≤ 1) wird sicher gestellt, dass die Amplitude immer positiv reell bleibt. 



Im Einzelnen sprechen wir von 

s(t) analog ⇒ AM (Amplitudenmodulation) 

s(t) digital ⇒ ASK (amplitude-shift keying – Amplitudenumtastung) 

Phasen- und Frequenzmodulation (Winkelmodulation): 

Alternativ zur Amplitude lässt sich auch 

die Phase oder Frequenz des Trägersignals modulieren. Die Amplitude ist dann konstant Û M (t) = 

Û M0 , und der Zeiger 

u(t) = Û M0 exp[jϕ(t)] (8) 

beinhaltet dann die modulierte Phase ϕ(t). Bei einer Phasenmodulation gilt 

mit dem Phasenhub ∆ϕ. 

Wir sprechen dann von 

s(t) analog ⇒ PM (Phasenmodulation) 

ϕ(t) = ∆ϕ · s(t) (9) 

s(t) digital ⇒ PSK (phase-shift keying – Phasenumtastung) 

Alternativ zur Phase können wir auch die Frequenz modulieren. Bei einer Frequenzmodulation 

führen wir zunächst die modulierte Frequenz f (t) 

ein, wobei f (t) dem Signal s(t) gemäß 

f (t) = 1 dϕ 

2π dt 

mit dem Frequenzhub ∆f T folgt. Wir sprechen dann von 

s(t) analog ⇒ FM (Frequenzmodulation) 

(10) 

f (t) = ∆f T · s(t) (11) 

s(t) digital ⇒ FSK (frequency-shift keying – Frequenzumtastung) 

2.1 Amplitudenmodulation 

Bei einem Zeiger u(t) gemäß Gl. (7) (d. h. u(t) positiv reell), folgt aus Gl. (5) für das modulierte 

Signal u M (t): 

d. h. 

u M (t) = Û M0 [1 + m · s(t)] cos(ω T t), (12) 

u M (t) = Û M0 cos(ω T t) + Û 

} {{ } M0 · m · s(t) cos(ω T t) 

} {{ } 

Träger 

Seitenbänder 

Das modulierte Signal besteht damit aus einem Träger sowie den Seitenbändern, die die Information 

s(t) beinhalten. Wenn wir die Fouriertransformierte von s(t) 

(13) 

s(t) ❞ S(jω) (14) 



einführen, ergibt sich als Foueriertransformierte von u M (t): 

u M (t) ❞ Û M0 {π[δ(ω − ω T ) + δ(ω + ω T )] + m } {{ } 2 [S(j(ω − ω T )) + S(j(ω + ω T ))]} (15) 

} {{ } 

Träger 

Seitenbänder 

mit der Dirac-Funktion δ(x). 

Das Spektrum von Gl. (15) ist in Abb. 2 skizziert (für f > 0). 

Träger 

S(j(ω − ω T )) 

f =0 

f T 

2∆f 

f = ω 2π 

Abb. 2: Spektrum eines amplitudenmodulierten Signals (dargestellt ist nur die positive Frequenzachse). 

Wenn das Ursprungssignal s(t) eine Bandbreite ∆f 

Hochfrequenz-Ebene die doppelte Bandbreite 2∆f für das modulierte Signal. 

aufweist, benötigt man nach Abb. 2 in der 

Ein weiterer Nachteil der normalen Amplitudenmodulation besteht darin, dass im Träger ein erheblicher 

Leistungsanteil steckt. 

Um dies zu illustrieren, nehmen wir ein harmonisches Basisbandsignal 

an, woraus sich ein u M (t) gemäßt Gl. (13) von 

s(t) = cos(ω 1 t) (16) 

u M (t) = Û M0 cos(ω T t) + Û M0 m cos(ω 1 t) cos(ω T t) (17) 

ergibt. Die mittlere Leistung von u M (t) lässt sich dann angeben als 

⎛ 

P ∝ u 2 M (t) = Û2 M0 

2 

⎞ 

⎜ 

⎝ }{{} 1 m 2 

+ ⎟ 

2 ⎠ 

Träger }{{} 

Seitenbänder 

Beispiel: Wenn wir einen Mittelwellen-AM-Sender mit einer Leistung von 500 kW und m = 0, 7 

annehmen, werden 400 kW im Träger und nur 100 kW in den Seitenbändern übertragen. 

Die normale Amplitudenmodulation (AM) ist deshalb eigentlich unwirtschaftlich. Ein sehr hoher Leistungsanteil 

wird nur für die Übertragung des Trägers verwendet (ohne Informationsanteil) und die 

Seitenbänder, die die eigentliche Information beinhalten, haben nur einen relativ kleinen Leistungsanteil. 

Weiterhin ist die benötigte Bandbreite doppelt so groß wie die Basisbandbreite. 

Trotzdem wird die AM noch viel verwendet im analogen Rundfunk im Bereich der LW (Langwelle), 

MW (Mittelwelle) und KW (Kurzwelle). Der Grund dafür liegt in der Verwendung sehr einfacher 



Rundfunkempfänger, bei denen aus dem hochfrequenten Signal u M (t) das Basisbandsignal mit |Û M (t)| 

durch lineare Hochfrequenzgleichrichtung (vgl. Abschnitt MI) gewonnen wird. 

Eine leichte Verbesserung bezüglich der übertragenen Trägerleistung lässt sich mit der dynamischen 

Amplituden-Modulation (DAM) erreichen, bei der die Trägerleistung bei geringerem Modulationsindex 

m herabgesetzt wird. 

2.1.1 Trägerlose Amplitudenmodulation 

Da der Träger keine Information überträgt, braucht er eigentlich auch nicht mit übertragen zu werden. 

Statt Gl. (13) erhält man dann 

u M (t) = Û M0 · m · s(t) cos(ω T t) (18) 

einfach aus der Multiplikation von s(t) mit cos(ω T t), was sich mit einer Mischschaltung (vgl. Abschnitt 

MI) einfach realisieren lässt. Das Spektrum der trägerlosen Amplitudenmodulation entspricht genau 

Abb. 2 ohne Träger. 

Der Nachteil der trägerlosen Amplitudenmodulation besteht darin, dass am Empfänger der Träger, also 

ein Signal ∝ cos(ω T t), wieder bereitgestellt werden muss. Dieses kann geschehen mit der Übertragung 

eines Träger-Restes (also Träger mit reduzierter Amplitude) und anschließender PLL (Phasenregelkreis, 

vgl. Abschnitt PLL). 

Mit einem derart im Empfänger wieder erzeugten Träger kann entweder ein Signal entsprechend Gl. 

(12) und (13) wieder erzeugt werden. Gl. (18) kann auch mit cos(ω T t) multipliziert und anschließend 

tiefpassgefiltert werden, um s(t) zurückzugewinnen. 

Der Nachteil der trägerlosen Amplitudenmodulation besteht darin, dass zwei Seitenbänder übertragen 

werden und damit wie bei der normalen AM eine Bandbreite von 2∆f benötigt wird. 

2.1.2 Einseitenbandmodulation 

Da beide Seitenbänder der trägerlosen AM die gleiche Information tragen, genügt es, nur eines der 

beiden Seitenbänder zu übertragen. Man spricht dann von der so genannten „Einseitenbandmodulation” 

(EM bzw. SSB – single-sideband modulation). 

Ein solches Einseitenband-Signal lässt sich z. B. aus einer trägerlosen AM mit anschließender Filterung 

gewinnen (siehe Abb. 3). 

Filter 

f =0 

f T 

2∆f 

f = ω 2π 

Abb. 3: Gewinnung eines Einseitenband-Signals aus der trägerlosen Amplitudenmodulation mit anschließender 

Filterung. 



Alternativ lässt sich ein Einseitenband-Signal auch mit einem so genannten „Quadraturmodulator” 

gewinnen, wie schematisch Abb. 4 zeigt. 

Abb. 4: Schematische Anordnung zur Gewinnung eines Einseitenband-Signals mit 

Quadraturmodulator. 

Diese Anordnung besteht aus zwei Multiplikatoren, die zur Multiplikation von cos(ω T t) bzw. sin(ω T t) 

mit s(t) bzw. dem um 90 ◦ verschobenen s(t) führen: Bei den beiden Multiplikationen entstehen jeweils 

zwei Seitenbänder, wobei bei der anschließenden Addition am Ausgang nur ein Seitenband übrig bleibt. 

Die Herausforderung der Realisierung von Abb. 4 besteht darin, über die gesamte Bandbreite von s(t) 

eine 90 ◦ -Verschiebung zu gewährleisten (eine 90 ◦ -Phasenverschiebung für alle Spektralkomponenten 

von s(t)). Das so erzeugte Signal s H (t) stellt dann die „Hilbert-Transformierte” von s(t) dar. 

Im Empfänger lässt sich das Basisbandsignal s(t) wieder gewinnen, indem das Einseitenband-Signal 

mit cos(ω T t) multipliziert wird. 

2.1.3 Restseitenbandmodulation 

Zur korrekten Rückgewinnung des Signals s(t) aus einem Einseitenband-Signal muss im Empfänger das 

Trägersignal mit der exakten Phase erzeugt werden. Dazu kann es zweckmäßig sein, einen Restträger 

mit zu übertragen. Weiterhin ist es gerade bei sehr breitbandigen Signalen (z. B. Video-Signalen) 

schwierig, entweder das Filter in Abb. 3 oder die 90 ◦ -Verschiebung genau so zu realisieren, dass nur 

genau ein Seitenband übrig bleibt. 

Es kann deshalb sinnvoll sein, neben dem oberen Seitenband auch einen Teil des unteren Seitenbands 

mit zu übertragen. Man spricht dann von „Restseitenbandmodulation” (auch VSB – vestigal-sideband 

modulation). 

Die Restseitenbandmodulation soll am Beispiel des analogen TV-Rundfunks (aktuell noch verwendet 

im Kabelfernsehen) erläutert werden. 

Im Abb. 5 ist das Restseitenband-modulierte Signal dargestellt, wobei das obere Seitenband (bezüglich 

des Bildträgers) vollständig erhalten ist, während das untere Seitenband durch ein Filter beschnitten 

ist. 



Bildträger 

Tonträger 

a) −1 0 1 2 3 4 5 6 MHz 

Bildträger 

Tonträger 

f − f T 

Nyquist-Flanke 

b) −1 0 1 2 3 4 5 6 MHz 

Tonträger 

f − f T 

c) 0 1 2 3 4 5 6 MHz 

f 

Abb. 5: Resteitenbandmodulation bei der analogen TV-Übertragung: a) Restseitenband-Signal, b) gefiltertes 

Restseitenband-Signal (mit Nyquist-Flanke) und c) Basisband-Signal am Mischerausgang. 

Dieses Signal aus Abb. 5a) wird durch ein Filter mit der so genannten „Nyquist-Flanke” geschickt, so 

dass dann das Spektrum in Abb. 5b) entsteht. 

Nach nachfolgender Mischung (Multiplikation mit dem Bildträger der Frequenz f T ) ergibt sich dann 

wieder das Basisband-Signal in Abb. 5c). 

2.2 Phasen- und Frequenzmodulation (Winkelmodulation) 

Bei einer Phasen- bzw. Frequenzmodulation ist der komplexe zeitabhängige Zeiger u(t) gemäß Gl. (8), 

also u(t) = Û M0 exp[jϕ(t)] gegeben, wobei entweder ϕ(t) oder dϕ 

dt 

proportional zum Basisband-Signal 

s(t) werden. 

Z. B. bei einem frequenzmodulierten Signal gilt mit den Gl. (10) und (11): 

dϕ 

dt = 2π∆f T · s(t) (19) 

bzw. für die Phase 

ϕ(t) = 2π∆f T 

∫ 

s(t) dt, (20) 

so dass man für das modulierte Signal 

u M (t) = R [ u(t) exp(jω T t) ] ∫ 

= Û M0 cos 

[ω T · t + 2π∆f T 

] 

s(t) dt 

(21) 

erhält. Die spektralen Eigenschaften von u M (t) lassen sich so nur schwer abschätzen, so das wir uns 

im folgenden zunächst auf die Analyse mit einem harmonischen Basisband-Signal beschränken wollen. 



2.2.1 Winkelmodulation mit harmonischem Signal s(t) 

Wir betrachten ein sinusförmiges s(t): 

s(t) = sin(ω 1 t), (22) 

so dass sich bei einer Phasenmodulation mit dem Phasenhub ∆ϕ ergibt: 

ϕ(t) = ∆ϕ sin(ω 1 t). (23) 

Diese Phasenmodulation lässt sich auch als eine Frequenzmodulation auffassen mit der Momentanfrequenz 

wobei 

f (t) = 1 dϕ 

2π dt = ∆ϕ · f 1 

} {{ } 

· cos(ω 1 t), (24) 

∆f T 

∆f T = ∆ϕ · f 1 (25) 

den Frequenzhub bezeichnet (f 1 = ω 1 

2π 

). Unter Berücksichtigung des Zusammenhangs zwischen Frequenzhub 

und Phasenhub in Gl. (25) sind Frequenz- und Phasenmodulation praktisch äquivalent. Zur 

Analyse des Spektrum eines phasenbzw. frequenzmodulierten Signals genügt es, das Spektrum von 

u(t) zu analysieren (Das Spektrum von u M (t) folgt dann durch Verschiebung um ±ω T ). 

u(t) ist gegeben als 

u(t) = Û M0 exp[jϕ(t)] = Û M0 exp[j∆ϕ sin(ω 1 t)] (26) 

u(t) ist damit periodisch mit der Frequenz ω 1 , so dass sich u(t) als Fourierreihe schreiben lässt: 

u(t) = 

Die Fourierkoeffizienten ergeben sich dann als 

mit der Besselfunktion J m (x), die gemäß 

J m (x) = 1 

2π 

+∞ ∑ 

m=−∞ 

U m exp(jmω 1 t). (27) 

U m = Û M0 J m (∆ϕ) (28) 

∫+π 

−π 

exp(jx sin(y) − jm · y) dy (29) 

definiert und in Abb. 6 für m = 0 . . . 5 dargestellt ist. Für negative Ordnungen m gilt J −m (x) = 

(−1) m J m (x). 

Gl. (27) besitzt unendlich viele Spektralkomponenten, so dass eigentlich zur Übertragung eines phasenbzw. 

frequenzmodulierten Signals eine unendlich große Bandbreite erforderlich ist. 

Beispielsweise zeigt Abb. 7 die Spektrallinien (ˆ=U m ) bei einer Phasenmodulation mit ∆ϕ = 5. 

Bei sehr hohen Ordnungen m werden die Spektrallinien immer kleiner, so dass sehr hohe Ordnungen 

vernachlässigt werden können. Eine gute Näherung besteht darin, alle Spektralkomponenten mit zu 

berücksichtigen, bei denen |J m (∆ϕ)| ≥ 0, 1 gilt, so dass sich dann die benötigte Bandbreite ∆f m zu 

∆f m ≈ 2f 1 (∆ϕ + 1) (30) 



J m 

J 0 

J 1 

J 2 

. 

J 3 

. 

J 4 

. 

J 5 

. 

Abb. 6: Besselfunktionen J m (x) der Ordnungen m = 0 . . . 5. 

x 

U m 

Û M0 

0, 1 

−0, 1 

−6 −4 −2 2 4 6 

m 

∆f m 

Abb. 7: Die Komponenten U m der Fourierreihe führen zu Spektralkomponenten von u(t) bei m · ω 1 

und von u M (t) bei (ω T + m · ω 1 ) und (−ω T − m · ω 1 ). Annahme: Phasenhub ∆ϕ = 5. 



ergibt, was im Beispiel von Abb. 7 (∆ϕ = 5) einem ∆f m = 12f 1 entspricht, so dass dort alle Ordnungen 

|m| ≤ 6 berücksichtigt werden. Bei einer Frequenzmodulation mit dem Zusammenhang zwischen 

Phasen- und Frequenzhub gemäß Gl. (25) führt Gl. (30) auf 

∆f m ≈ 2(f 1 + ∆f T ). (31) 

Eine Frequenzmodulation ist einfach möglich mit einem spannungsgesteuerten Oszillator, und die 

Demodulation kann einfach mit einer PLL (vgl. Abschnitt PLL) erfolgen. 

Beispiel: FM-Rundfunk; hier gilt für die maximale Modulationsfrequenz f 1 ≈ 15 kHz, der Frequenzhub 

ist ∆f T = 75 kHz, woraus sich eine HF-Bandbreite von ∆f m = 180 kHz ergibt. 

3 Bewertung analoger Modulationsverfahren 

Für die Bewertung der Modulationsverfahren ist bei gegebener Basisbandbreite ∆f einmal die benötigte 

Hochfrequenzbandbreite ∆f m von Interesse. Weiterhin ist von Interesse, welches Signal/Rausch- 

Verhältnis im Basisband nach der Demodulation bei einem gegebenen Signal/Rausch-Verhältnis in der 

Hochfrequenz-Ebene erreicht werden kann. 

S HF ,W HF 

> Demodulator 

S 

N ∣ 

HF 

S NF ,W NF 

S 

∣ 

N 

∣ 

NF 

Abb. 8: Empfänger mit Demodulator. 

Dieser Zusammenhang soll mit Hilfe von Abb. 8 erläutert werden. Wir haben zunächst auf der 

Hochfrequenz-Ebene eine Signalleistung S HF und eine spektrale Rauschleistungsdichte W HF vorliegen, 

so dass wir mit der Hochfrequenzbandbreite ∆f m auf der Hochfrequenzseite ein Signal/Rausch- 

Verhältnis von 

S 

N 

= 

∣ HF 

S HF 

W HF · ∆f m 

(32) 

erhalten. Nach der Demodulation ergibt sich auf der Niederfrequenzseite 

S 

N 

= 

S NF 

∣ W NF · ∆f , (33) 

NF 

und man kann nun für die verschiedenen Modulationsverfahren einen Störabstands-Verbesserungs- 

Faktor einführen, der die Signal/Rausch-Verhältnisse auf der Hochfrequenz- und Niederfrequenz-Ebene 

zueinander in Beziehung setzt. Wir wollen hier einen modifizierten Verbesserungsfaktor V gemäß 

V = S S 

NF /W NF N ∣ 

= NF 

∆f 

S HF /W HF 

S ∣ 

(34) 

∆f m 

N ∣ HF 



einführen, der die Signalleistungen mit den jeweiligen spektralen Rauschleistungsdichten verknüpft. 

Zur Analyse gehen wir vereinfachend von einem harmonischen Basisband-Signal s(t) = sin(ω 1 t) aus: 

Als Referenz dient die Einseitenbandmodulation, bei der trivialerweise mit V = V EM 

V EM = 1 (35) 

gilt, da bei der Einseitenbandmodulation das Spektrum nur verschoben wird. In diesem Sinn gibt V 

gerade den Faktor an, um den sich bei gegebener Hochfrequenzleistung S HF das Signal/Rausch- 

Verhältnis nach dem Demodulator verbessert. Für die Amplitudenmodulation gilt 

V AM = m2 /2 

, (36) 

1 + m2 

2 

und damit V AM < 1, was im Wesentlichen daran liegt, dass ein hoher Anteil der Hochfrequenzleistung 

für die Übertragung des Trägers aufgebracht werden muss. Beim Vergleich mit Gl. (17) entspricht 

V AM gerade dem Leistungsanteil in den Seitenbändern im Vergleich zur Gesamtleistung. Bei Phasenmodulation 

gilt (ohne Beweis) 

V P M = ∆ϕ2 

2 . (37) 

Für kleine Phasenhübe ∆ϕ ≪ 1 verhält sich eine Phasenmodulation genau so wie eine Amplitudenmodulation 

mit m = ∆ϕ. 

Bei einer Frequenzmodulation ist zu berücksichtigen, dass der Phasenhub ∆ϕ bei gegebenem Frequenzhub 

∆f T gemäß Gl. (25) von der Modulationsfrequenz f 1 abhängt. Wenn man über alle Modulationsfrequenzen 

innerhalb der Bandbreite ∆f mittelt, ergibt sich aus Gl. (37) mit ∆ϕ = ∆f T /f 1 aus 

Gl. (25) 

zu 

1 

= 1 

V F M ∆f 

∫∆f 

0 

1 

V P M (f 1 ) df 1 = 1 

∆f 

V F M = 3 2 

∫∆f 

0 

( 

∆fT 

∆f 

2 

∆ϕ 2 df 1 = 1 

∆f 

∫∆f 

0 

2f 2 

1 

∆f 2 T 

df 1 (38) 

) 2 

. (39) 

Für das oben angegebene Beispiel des FM-Rundfunks ergibt sich mit ∆f T = 75 kHz und ∆f = 15 kHz 

ein V F M = 37, 5 ( ˆ=15, 7 dB). Dies bedeutet bei gegebener Hochfrequenzleistung ein um den Faktor 

37, 5 höheres erreichbares Signal/Rausch-Verhältnis im Basisband als bei Einseitenbandmodulation. 

Für diese Erhöhung des Signal/Rausch-Leistungs-Verhältnisses muss man aber mit der erhöhten 

Hochfrequenzbandbreite ∆f m gemäß Gl. (31) bezahlen. 

Die Erzielung des Verbessungsfaktors gemäß Gl. (37) und (39) bei Phasen- bzw. Frequenzmodulation 

setzt allerdings voraus, dass das Signal/Rausch-Leistungs-Verhältnis auf der Hochfrequenzseite 

S 

∣ ≥ 1 ist. Man spricht dabei von der so genannten „FM-Schwelle”. Oberhalb dieser FM-Schwelle 

HF 

N 

sind sogar noch höhere Verbesserungsfaktoren als in Gl. (39) möglich, wenn die höheren Modulationsfrequenzen 

bei der Modulation angehoben werden und bei der Demodulation wieder abgesenkt werden 

(Präemphase/Deemphase). 



4 Digitale Modulationsverfahren 

Auch bei den bisher diskutierten Modulationsverfahren kann das Basisband-Signal s(t) sowohl analoger 

als auch digitaler Natur sein. Für digitale Modulationsverfahren sind aber insbesondere PSK, 

QAM (Quadratur-Amplituden-Modulation) und OFDM (orthogonal frequency-division multiplex) von 

Interesse. 

4.1 Phasenumtastung (PSK) 

Wir gehen wieder vom modulierten Signal entsprechend Gl. (5) mit dem komplexen Zeiger u(t) aus. 

Bei einer reinen Phasenumtastung bleibt die Amplitude |u(t)| konstant, und nur die Phase ändert sich, 

so dass sich bei binärer PSK in der komplexen Ebene ein u(t) wie in Abb. 9 ergibt. 

I(u) 

−Û M0 

Û M0 

0 1 

R(u) 

Abb. 9: Binäre Phasenumtastung (PSK). 

Der Zeiger u(t) ist dabei u(t) = Û M0 exp(j · 0) für die „1” und u(t) = Û M0 exp(j · π) für die „0”. 

Diese binäre Phasenumtastung entspricht praktisch einer trägerlosen Amplitudenmodulation (bzw. 

-umtastung), da u(t) zwischen u(t) = Û M0 und u(t) = −Û M0 umgestastet wird. 

Es entstehen wie bei der normalen trägerlosen Amplitudenmodulation zwei Seitenbänder, die die gleiche 

Information tragen. Weiterhin ist wegen der binären Modulation die Symbolrate (in Baud oder Bd) 

gleich der Bitrate. 

Um mehr Informationen pro Symbol zu übertragen, kann man auch pro Symbol eine Quantisierung in 

mehr Phasenzustände vornehmen. Ein Beipiel dafür ist die quaternäre Phasenumtastung (QPSK) in 

Abb. 10. Pro Symbol können hier vier unterschiedliche Phasen und damit 2 bit übertragen werden. 

Die Bitrate wird damit doppelt so groß wie die Symbolrate. 

Sowohl R[u(t)] als auch I[u(t)] besitzen jeweils zwei Zustände, mit denen sich das modulierte Signal 

u M (t) in Gl. (5) schreiben lässt: 

u M (t) = R[u(t) exp(jω T t)] 

= R[u(t)] cos(ω T t) − I[u(t)] sin(ω T t) (40) 

Das Signal in Gl. (40) lässt sich einfach mit einem Quadraturmodulator (vgl. Abb. 4) erzeugen, wie 



I(u) 

01 

11 

R(u) 

00 

10 

Abb. 10: Quaternäre Phasenumtastung (QPSK). 

Abb. 11 zeigt. Bei der QPSK sind sowohl R[u(t)] als auch I[u(t)] binäre Signale, aus denen schließlich 

das quaternäre modulierte Signal u M (t) erzeugt wird. 

Abb. 11: Quadraturmodulator zur Gewinnung von QPSK- oder QAM-Signalen. 

Auch bei der QPSK ist wie bei der binären PSK der Träger unterdrückt. 1 Allerdings enthalten das 

obere und untere Seitenband der QPSK unterschiedliche Informationen. 

4.2 Quadratur-Amplitudenmodulation (QAM) 

Um pro Symbol noch mehr Zustände übertragen zu können, ist es zweckmäßig, sowohl die Amplitude 

als auch die Phase zu variieren, und man gelangt so beispielsweise zur Quadratur-Amplitudenmodulation 

(QAM). Das Konstellationsdiagramm einer 16-QAM zeigt Abb. 12. Sowohl der R[u(t)] als auch der 

I[u(t)] weisen vier Zustände auf, und das modulierte Signal kann dann wieder wie in Abb. 11 erzeugt 

1 Dies gilt zumindest, wenn alle Zustände gleich wahrscheinlich sind. 



werden. 

I(u) 

R(u) 

Abb. 12: Konstellationsdiagramm einer 16-QAM (Quadratur-Amplitudenmodulation). 

Bei einer 16-QAM werden pro Symbol 4 bit übertragen, so dass die Bitrate viermal so groß wie die 

Symbolrate wird. 

Mit zunehmender Anzahl verschiedener Zustände pro Symbol steigt zwar bei gegebener Symbolrate 

(und damit gegebener Hochfrequenzbandbreite) die Bitrate an, aber auch die Anforderungen an das 

Signal-Rauschleistungs-Verhältnis ( S N ) steigen. 

Modulationsverfahren binäre PSK QPSK 16-QAM 64-QAM 

benötigtes S N 

9 dB 12 dB 19 dB 25 dB 

Tabelle 1: Erforderliches S N 

bei unterschiedlichen Modulationsverfahren für eine Fehlerhäufigkeit von 

10 −4 (Meinke,Gundlach, Taschenbuch der Hochfrequenztechnik, Springer 1992, S. O 28). 

4.3 OFDM (orthogonal frequency-division multiplex) 

In der terrestrischen Funkübertragung gibt es häufig das Problem der so genannten „Mehrwegeausbreitung”, 

wie schematisch Abb. 13 zeigt. 

Zwischen Sender und Empfänger gibt es beispielsweise einen direkten Pfad mit der Laufzeit τ und 

einen weiteren Signalweg der Laufzeit τ + ∆τ, so dass sich dann eine Impulsantwort der Länge ∆τ 

ergibt. Für eine eindeutige Übertragung mit geringem Symbolnebensprechen ist es dann zweckmäßig, 

ein Modulationsverfahren mit einer Symboldauer T S größer als ∆τ bzw. einer Symbolrate kleiner als 

1 

∆τ 

zu verwenden. 

Um bei geringen Symbolraten trotzdem hohe Datenraten zu übertragen, wird häufig die so genannte 

„orthogonal frequency-division multiplex” (OFDM)-Modulation angewandt. Dazu wird das modulierte 

Signal in sehr viele (z. B. > 1000) Hochfrequenz-Subträger aufgeteilt, die dann jeder für sich mit 

QPSK oder QAM geringerer Daten- bzw. Symbolrate moduliert werden. 

Das modulierte Signal u M (t) lässt sich dann wieder ähnlich wie in Gl. (5) mit u(t) darstellen: 

u M (t) = R[u(t) exp(jω T t)], (41) 



Sendeantenne 

τ 

τ + ∆τ 

Empfangsantenne 

Abb. 13: Problem der Mehrwegeausbreitung: Das Signal erreicht den Empfänger auf unterschiedlichen 

Wegen und damit zu verschiedenen Zeitpunkten. 

wobei sich 

u(t) = 

N−1 ∑ 

n=0 

U n exp(j2π · n · δf · t) (42) 

aus N Subträgern der jeweiligen Frequenzen n · δf zusammensetzt. U n ist z. B. entsprechend einer 

QAM kodiert und bleibt jeweils für eine Symboldauer T S = 1 

δf 

konstant. Das Spektrum eines solchen 

OFDM-Signals ist in Abb. 14 skizziert. 

δf 

f T + n · δf 

. . . . . . 

f T = ω T 

2π 

f n = N · δf 

f 

Abb. 14: Schematische Darstellung eines OFDM-Spektrums. 

Das gesamte Spektrum das OFDM-Signals hat eine Breite von N · δf = f n . Die Übertragung dieses 

Signals u(t) erfolgt dann zeitdiskret (t = i · ∆t mit Zeitintervallen ∆t = 1 f n 

= 1 

N·δf 

= T S 

N 

). 

Für t = i · ∆t stellt Gl. (42) eine diskrete Fouriertransformation zwischen U n und u(i · ∆t) dar, so dass 

sich u(t) und damit das modulierte Signal u M (t) durch eine inverse FFT (fast Fourier transform) und 

eine Quadratur-Amplitudenmodulation leicht gewinnen lässt, wie Abb. 15 zeigt (vgl. auch Abb. 11). 

Am Empfänger können die Daten U 0 . . . U N−1 wieder durch eine Fouriertransformation gewonnen 

werden. 

In der obigen vereinfachten Betrachtung sind wir von einer Symbolrate von 1 

T S 

= δf ausgegangen. 

Tatsächlich ist die praktisch übertragene Symbolrate etwas geringer, da zwischen den Symbolen noch 

Schutzintervalle eingeführt werden. Für das Beispiel der Mehrwegeausbreitung in Abb. 13 sollte das 



Abb. 15: Prinzip der Gewinnung eines OFDM-Signals. 

Schutzintervall länger als ∆τ sein, um ein Übersprechen aufeinander folgender Symbole zu vermeiden. 

Beispiele für OFDM-Übertragung sind z. B. DAB (digital audio broadcast), DRM (digital radio mondiale), 

DVB-T (digital video broadcast-terrestrial) oder DSL (digital subscriber line). 


Hochfrequenztechnik II Phasenregelkreise (PLL) PLL/1 

Der Zweck eines Phasenregelkreises (englisch phase–locked– loop = PLL) besteht darin, ein Oszillatorsignal 

zu generieren, das frequenz- und phasenrichtig mit dem Eingangssignal übereinstimmt. 

Anwendungsbeispiele: PM-Demodulation, FM-Demodulation, Trägerrückgewinnung, Taktrückgewinnung 

bei Puls-Code-modulierten Signalen, Frequenzsynthese 

1 Arbeitsprinzip 

Das Prinzip eines Phasenregelkreises ist im Bild 1 dargestellt. 

Abb. 1: Darstellung eines Phasenregelkreises (PLL) 

Ein Phasenregelkreis besteht aus dem Phasendifferenzdetektor, dessen Ausgangssignalu 3 (t) ist im wesentlichen 

proportional zur Phasendifferenz [ ϕ i (t)−ϕ a (t) ] , dem Schleifenfilter (im allgemeinen ein 

Tiefpaßfilter) mit der ÜbertragungsfunktionF(s), (s–komplexe Frequenzs=jω+σ) und dem spannungsgesteuerten 

Oszillator (VCO = voltage controlled oscillator), dessen Ausgangsfrequenz durch die 

Spannungu 4 (t) gesteuert wird. Ungewöhnlich ist bei einem Phasenregelkreis, daß als Eingangssignale 

zeitabhängige Winkelϕ i (t),ϕ a (t) vorliegen. Bei Annahme harmonischer Spannungenu 1 (t),u 2 (t) 

sind diese zu verstehen gemäß 

u 1 (t)=Û 1 cos ( ω 0 t+ϕ i (t) ) bzw. u 1 (t)=Û 1 sin ( ω 0 t+ϕ i (t) ) (1) 

und 

u 2 (t)=Û 2 cos ( ω 0 t+ϕ a (t) ) bzw. u 2 (t)=Û 2 sin ( ω 0 t+ϕ a (t) ) (2) 

mit den Momentanfrequenzen (vgl. FM-Modulation) 

ω i (t)=ω 0 +dϕ i /dt (3) 

ω a (t)=ω 0 +dϕ a /dt (4) 

ω 0 ist dabei eine Bezugsfrequenz (z.B. eine mittlere Frequenz des VCO füru 4 =0). Die Wirkungsweise 

des Phasenregelkreises ist dabei so zu verstehen, daß bei einer Phasendifferenzϕ i −ϕ a =0 einu 3 (t) 

und schließlich einu 4 (t) entsteht, so daß die Frequenzω a (t) des VCO’s und gemäß Gl.(4) auch 



ϕ a (t) so geändert wird, bis schließlichϕ i −ϕ a =0 oder zumindest eine konstante Regelabweichung 

ϕ i −ϕ a =const erreicht wird. Die Phasen sind zeitabhängige Größenϕ i (t),ϕ a (t). Für eine Analyse 

des Regelverhaltens des Phasenregelkreises ist jedoch ähnlich wie bei konventionellen Netzwerken eine 

Analyse im Frequenzbereich zweckmäßig. Mit der komplexen Frequenzs=jω+σ werden deshalb im 

folgenden die Laplace-Transformierten vonϕ i (t),ϕ a (t) gemäßφ i (s),φ a (s) eingeführt. 

2 Multiplizierender Phasendifferenzdetektor 

Während in Bild 1 die Realisierung des Schleifenfilters und des VCO’s (z.B. Ansteuerung über spannungsabhängige 

Kapazität in Form einer Kapazitätsdiode) geläufig ist, stellt der Phasendifferenzdetektor 

eine zunächst ungewöhnliche Komponente dar. Eine Möglichkeit zur Realisierung eines Phasendifferenzdetektors 

stellt die Verwendung eines Multiplizierers dar (auch als ”lineare” PLL bezeichnet, 

da im Sinne der IC-Technologie lineare bzw. analoge IC’s verwendet werden). Mit 

u 1 (t)=Û 1 sin ( ω 0 t+ϕ i (t) ) (5) 

und 

u 2 (t)=Û 2 cos ( ω 0 t+ϕ a (t) ) (6) 

ergibt die Multiplikation 

u 1 (t)u 2 (t)= 1 2Û1Û2 

( sin(ϕi −ϕ a )+sin(2ω 0 t+ϕ i +ϕ a ) ) (7) 

Der Signalanteil bei der doppelten Frequenz2ω 0 wird entweder durch das Schleifenfilter oder ein 

separates Filter weggefiltert, so daß nur der erste Teil verbleibt und man so mitu 3 (t)=K 3 u 1 (t)u 2 (t) 

einen Phasendifferenzdetektor mit 

u 3 (t)=K d sin ( ϕ i (t)−ϕ a (t) ) (8) 

erhält, wobei die KonstanteK d gemäß 

K d = 1 2 K 3Û1Û2 (9) 

gegeben ist. 

3 Linearisierte Beschreibung 

Für einen idealen Phasendifferenzdetektor wäre 

u 3 (t)=K d 

( 

ϕi (t)−ϕ a (t) ) (10) 

bzw. im Frequenzbereich 

U 3 (s)=K d 

( 

φi (s)−φ a (s) ) (11) 

mit der KonstantenK d . Das mit der Phase periodische Verhalten vonu 1 (t),u 2 (t) hat zur Folge, daß 

die Phasendifferenz nur bis maximal±π eindeutig definiert werden kann (abhängig vom Typ des Phasendifferenzdetektors; 

bei einem multiplizierenden Phasendifferenzdetektor ist der Linearitätsbereich 



gemäß Gl.(8) sogar nur auf ca.±1rad beschränkt). Im Rahmen der linearen Analyse sollen deshalb 

zunächst derart kleine Phasendifferenzen vorangesetzt werden. Im Rahmen von Bild 1 gilt weiterhin: 

U 4 (s)=F(s)U 3 (s) (12) 

Für den spannungsgesteuerten Oszillator gilt in der linearen Näherung 

ω a (t)=ω 0 +K 0·u 4 (t) (13) 

wenn die Referenzfrequenzω 0 so gewählt wird, daßω a =ω 0 füru 4 =0. Gl.(13) läßt sich mit Gl.(4) 

auch schreiben als 

dϕ a 

=K 0 u 4 (t) (14) 

dt 

so daß sich nach Transformation in dem Frequenzbereich 

s·φ a (s)=K 0 U 4 (s) (15) 

ergibt (Ableitung nach der Zeit entspricht der Multiplikation mit s im Frequenzbereich). Kombination 

der Gl.(11),(12),(15) führt auf die Übertragungsfunktion von der Eingangsphaseϕ i (t) zur Ausgangsphaseϕ 

a (t) gemäß 

mit der Schleifenverstärkung 

φ a (s) 

φ i (s) 

=H(s)= 

G(s) 

1+G(s) 

(16) 

G(s)=K 0 K d F(s)/s (17) 

Für die Stabilität gelten die normalen Netzwerkbetrachtungen, d.h.H(s) darf keine Pole in der rechten 

s-Halbebene aufweisen. DaF(s) ein Tiefpaßverhalten aufweist, wirdF(s) und damit auchσ(s) mit 

zunehmender Frequenzω(mits=jω) kleiner, so daßϕ a (t) (bzw.φ a (s)) insbesondere bei kleinen 

Frequenzen (kleines) der Eingangsphaseϕ i (t) (bzw.φ i (s)) sehr genau folgt. Für höhere Frequenzen 

wird die Regelabweichung größer und man definiert eine Grenzfrequenzω g des Phasenregelkreises, 

wenn 

wird. 

|G(s=jω g )|=1 (18) 

4 Statischer Phasenfehler 

Wir nehmen an, die PLL sei bei konstanter Eingangsfrequenz eingerastet (d.h.ω i =ω a bzw.dϕ i /dt= 

dϕ a /dt), die Frequenzω i =ω a weiche aber um 

∆ω 0 =ω a −ω 0 (19) 

von der Referenzfrequenzω 0 ab. Eine statische Lösung der PLL bietet dann 

u 3 = K d (ϕ i −ϕ a ) (20) 

u 4 = F(s=0)u 3 (21) 



und gemäß Gl.(13) 

∆ω 0 =ω a −ω 0 =K 0·u 4 (22) 

Die Größe des statischen Phasenfehlers ergibt sich dann aus Gl.(21) - (22) zu 

(ϕ i −ϕ a )= 

∆ω 0 

K d K 0 F(s=0) 

(23) 

der genügend klein bleiben muß, damit der Phasendifferenzdetektor im linearen Bereich verbleibt (z.B. 

|ϕ i −ϕ a |≤1rad für den multiplizierenden Phasendifferenzdetektor). 

Um möglichst große Frequenzabweichungen∆ω 0 zulassen zu können (vergleiche auch weiter unten 

die Diskussion über den Haltebereich), sollteF(s=0) möglichst groß sein, weshalb Filter mit integrierendem 

Anteil vorteilhaft sind. 

5 Schleifenfilter 

Das Schleifenfilter mit der ÜbertragungsfunktionF(s) ist normalerweise ein Filter 1. Ordnung mit der 

Übertragungsfunktion 

F(s)=K n 

s+ω 2 

s+ω 1 

(24) 

Für einen verschwindenden Phasenfehler gemäß Gl.(23) ist man an einem integrierenden Filter mit 

ω 1 →0, d.h. 

s+ω 2 

F(s)=K n 

s 

interessiert, welches beispielsweise gemäß Bild 2 

(25) 

Abb. 2: Realisierungsmöglichkeit für ein integrierendes Tiefpaßfilter 1. Ordnung 

als aktives Filter mit 

K n = R 2 

R 1 

; ω 2 = 1 

R 2 C 

realisiert werden kann. Für die SchleifenverstärkungG(s) gemäß Gl.(17) gilt mit Gl.(25) 

(26) 

G(s)=K(s+ω 2 )/s 2 (27) 

mit 

K=K d K n K 0 (28) 



und für die Phasenübertragungsfunktion gemäß Gl.(16) ergibt sich eine Übertragungsfunktion 2. Ordnung 

H(s)= G(s) 

1+G(s) = K·s+K·ω 2 

s 2 +K·s+K·ω 2 

(29) 

Abb. 3: SchleifenverstärkungG(jω) und PhasenübertragungsfunktionH(jω) 

(Zur Beschreibung der Übertragungsfunktion werden in der Literatur auch die Abkürzungenω n = 

√ √ 

Kω2 undζ=0.5 K 

ω 2 

verwendet). Die Grenzfrequenzω g des Phasenregelkreises gemäß Gl.(18) mit 

|G(s=jω g )|=1 ergibt sich fürω 2


Abb. 4: Ausgangsphaseϕ a (t) für einen Einheitssprung der Eingangsphaseϕ i (t) 

6 Einrastprobleme 

Da bei starken Frequenzänderungen am Eingang wegenϕ= ∫ ∆ωdt erhebliche Phasenänderungen entstehen, 

kann der lineare Bereich der PLL leicht verlassen werden, so daß es dann zu Einrastproblemen 

kommt. Das Einrastverhalten hängt in starkem Maße von der Art des verwendeten Phasendifferenzdetektors 

ab, wobei die folgende Diskussion am Beispiel des unter 2. beschriebenen multiplizierenden 

Phasendifferenzdetektors erfolgt. 

6.1 Haltebereich 

Der Haltebereich bezeichnet den Bereich, in dem die PLL langsamen Frequenzänderungen des Eingangssignals 

sicher folgen kann. Wenn Gl.(23) für den multiplizierenden Phasendifferenzdetektor ausgewertet 

wird, ergibt sich eigentlich 

sin(ϕ i −ϕ a )= 

so daß wegensin(ϕ i −ϕ a )


maximale Frequenzänderung∆ω=∆ω L , so daß die PLL innerhalb einer Periode der Differenzfrequenz 

∆ω einrastet. 

6.2.1 Intuitive Herleitung 

Wenn am Eingang des Phasendifferenzdetektorsu 1 (t) undu 2 (t) sich in der Frequenz um∆ω unterscheiden, 

entsteht am Ausgang des multiplizierenden Phasendifferenzdetektors 

u 3 (t)=K d sin(∆ωt+ψ 3 ) (34) 

mit einer zunächst willkürlichen Phaseψ 3 . Das FilterF(s) überträgt nunu 3 (t) mits=j∆ω, so daß 

sich 

u 4 (t)=K d |F(j∆ω)|sin(∆ωt+ψ 4 ) (35) 

ergibt, womit der VCO gemäß Gl.(13) als Ausgangsfrequenz liefern würde: 

ω a (t)=ω 0 +∆ω a sin(∆ωt+ψ 4 ) (36) 

mit 

∆ω a =K 0 K d |F(j∆ω)| (37) 

Die Betrachtung ist insofern grob vereinfacht, da eine Modulation vonω a (t) sofort auch die Differenzfrequenz 

und damit∆ω moduliert. Innerhalb des Fangbereichs∆ω∆ω, so daß die 

Frequenzvariation des VCO ausreicht, um den anfänglichen Frequenzsprung∆ω auszugleichen. Der 

Fangbereich∆ω L ist nur erreicht, wenn∆ω a =∆ω wird, so daß gilt: 

∆ω a =∆ω= ! ∆ω L (38) 

und sich so∆ω L gemäß 

∆ω L =K 0 K d |F(j∆ω L )| (39) 

ergibt. Ein Vergleich mit Gl.(17), (18) zeigt, daß damit der Fangbereich 

∆ω L =ω g (40) 

durch die Grenzfrequenz der PLL gegeben ist. Bild 5 skizziert grobω 2 (t) für einen Frequenzsprung 

vonω 1 um∆ω=∆ω L . 

6.2.2 PLL-Antwort auf einen Frequenzsprung am Eingang 

Um die Dynamik einer PLL noch besser zu verstehen, sollω a (t) bei einem Frequenzsprung vonω i (t) 

im Rahmen der linearisierten Beschreibung (Abschnitt 3) analysiert werden. Fürt0 (42) 



Abb. 5: Vereinfachtes Einrastverhalten für∆ω=∆ω L innerhalb des Fangbereichs 

und damit 

ϕ i =∆ω·t für t>0 (43) 

Die Laplace- Transformation von Gl.(43) liefert 

woraus sich die VCO-Ausgangsphase 

φ i (s)=∆ω/s 2 (44) 

φ a (s)=φ i (s)H(s) (45) 

ergibt. Wir sind an der Ausgangsfrequenzω a (t) interessiert (vgl.Gl.(4)): 

ω a (t)−ω 0 =dϕ a /dt , (46) 

so daß es zweckmäßig ist, die LaplacetransformierteΩ a (s) von [ ω a (t)−ω 0 

] einzuführen, so daß aus 

Gl.(46) folgt: 

Ω a (s)=sφ a (s) (47) 

(Differentiation nach t entspricht nach Laplace-Transformation Multiplikation mit s). Mit Gl.(46), 

(47) gilt damit 

MitH(s) gemäß Gl.(28) undω 2 =K/4 folgt dann 

Ω a (s)= ∆ω 

s 

Ω a (s)=sφ i (s)H(s) (48) 

Ks+Kω 2 

s 2 = ∆ω·K 

+Ks+Kω 2 s 

woraus sich nach Rücktransformation in den Zeitbereich ergibt 

s+K/4 

( s+K/2 

) 2 

(49) 

{ 

ω a (t)−ω 0 =∆ω 1−e −Kt/2[ 1−Kt/2 ]} ,t>0 (50) 



Für den Phasenfilter gilt entsprechend: 

φ i (s)−φ a (s)=φ i (s) ( 1−H(s) ) = 

∆ω 

( s+K/2 

) 2 

(51) 

woraus sich im Zeitbereich 

ϕ i (t)−ϕ a (t)= ∆ω 

K Kte−Kt/2 (52) 

ergibt. Das Einrastverhalten gemäß Gl.(50), (52) ist in Bild 6 dargestellt. 

Abb. 6: Verlauf vonω a (t) für einen Frequenzsprung vonω i (t) zur Zeitt=0und zugehöriger Phasenfilter 

[ ϕ i (t)−ϕ a (t) ] für ein integrierendes PLL-Filter 1. Ordnung mitω 2 =K/4 

Falls sich∆ω gerade am Rand des Fangbereichs mit∆ω=∆ω L =ω g ≃K befindet, wird der maximale 

Phasenfehler(ϕ i −ϕ a ) max =0,736, so daß die linearisierte Beschreibung für den Phasendifferenzdetektor 

noch einigermaßen gültig ist und auch der Verlauf vonω 2 (t) gemäß Bild 6 recht gut der 

intuitiven Darstellung in Bild 5 entspricht. 

6.3 Ziehbereich 

Auch für∆ω>∆ω L ist ein Einrasten der PLL unter Umständen bis zu∆ω


Abb. 7: Einrastvorgang innerhalb des Ziehbereichs mit∆ω L ω a und einu 3


Abb. 8: Realisierung eines 3-Zustands-Phasendifferenzdetektors 

Abb. 9: Zustandsdiagramm des Phasendifferenzdetektors nach Bild 8 

weise des Phasendifferenzdetektors seien zunächst gleiche Frequenzenω i =ω a vonu 1 ,u 2 angenommen, 

wobeiu 1 gegenüberu 2 umπ/2 nacheilt (ϕ i −ϕ a =−π/2 ): 

Es ergibt sich somit ein=0,=0,25 und damit gemäß Gl.(54): 

u 3 =−π/2K d (55) 

Tatsächlich ergibt sich ein linearer Arbeitsbereich 

u 3 =K d (ϕ i −ϕ a ) für |ϕ i −ϕ a |ω a die Anstiegsflanken vonu 1 , so daß 

der Phasendifferenzdetektor nur die Zustände 2 und 3 annimmt und damit wie gefürchtetu 3 >0wird, 

während fürω i


Abb. 10: Arbeitsweise des 3-Zustands-Phasendifferenzdetektors fürω i =ω a 

7 Anwendungen 

7.1 Demodulation phasenmodulierter Signale 

Eine Demodulation von analog PM- oder digital PSK-modulierten Signalen ist in einfacher Weise nach 

dem Phasendifferenzdetektor möglich, da 

u 3 =K d (ϕ i −ϕ a ) (57) 

unmittelbar der modulierten Signalphaseϕ i (t) folgt, solange nurϕ a ≃ constant ist. Deshalb ist für 

die Übertragungsfunktion 

φ a (s) 

φ i (s) 

=H(s)≃0 (58) 

im interessierenden Frequenzbereich zu finden, d.h. die PLL- Grenzfrequenzω g muß kleiner als die 

untere Grenzfrequenz des phasenmodulierten Signals sein. 

7.2 Demodulation frequenzmodulierter Signale 

Die Demodulation frequenzmodulierter Signale ist in einfacher Weise möglich, wenn 

φ a (s) 

φ i (s) 

=H(s)≃1 (59) 

und damit 

ω a (t)≃ω i (t) (60) 

innerhalb des Modulationsfrequenzbereichs gilt. Dau 4 (t) linear mitω a (t) verknüpft ist, läßt sich dann 

das demodulierte Signal mitu 4 (t) gewinnen. Die PLL-Grenzfrequenzω g muß größer sein als die obere 



Modulationsfrequenz der FM-Modulation. Weiterhin ist sicherzustellen, daß auch bei hohen Frequenzsprüngen 

die PLL eingerastet bleibt, wofür∆ω t

gesamtes Skript (PDF, 3,4 MB) - TU Berlin

Erfolgreiche ePaper selbst erstellen

Template löschen?

Als Template speichern?