Teilchen im Kasten
Teilchen im Kasten
Teilchen im Kasten
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
6. Das <strong>Teilchen</strong> <strong>im</strong> Potentialkasten<br />
6.1 Der eind<strong>im</strong>ensionale <strong>Kasten</strong><br />
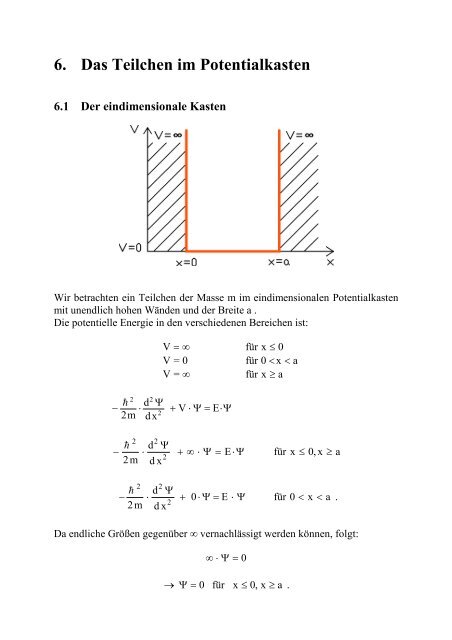
Wir betrachten ein <strong>Teilchen</strong> der Masse m <strong>im</strong> eind<strong>im</strong>ensionalen Potentialkasten<br />
mit unendlich hohen Wänden und der Breite a .<br />
Die potentielle Energie in den verschiedenen Bereichen ist:<br />
V = ∞<br />
für x ≤ 0<br />
V = 0<br />
für 0 < x < a<br />
V = ∞<br />
für x ≥ a<br />
−<br />
h 2<br />
2<br />
2<br />
2<br />
d Ψ<br />
⋅<br />
m d x<br />
+ V ⋅ Ψ = E⋅Ψ<br />
2<br />
2<br />
d Ψ<br />
− h ⋅<br />
2 m<br />
2<br />
d x<br />
+<br />
∞ ⋅ Ψ =<br />
E⋅Ψ<br />
für<br />
x<br />
≤<br />
0, x<br />
≥<br />
a<br />
2<br />
2<br />
d Ψ<br />
− h ⋅ + 0 ⋅ Ψ = E ⋅ Ψ für 0 < x < a .<br />
2 m<br />
2<br />
d x<br />
Da endliche Größen gegenüber ∞ vernachlässigt werden können, folgt:<br />
∞ ⋅ Ψ = 0<br />
→ Ψ = 0 für x ≤ 0, x ≥ a .
Die zweite Gleichung ergibt mit<br />
α 2 = 2mE / h<br />
2<br />
d<br />
2<br />
Ψ = − α<br />
2<br />
2<br />
d x<br />
Ψ<br />
.<br />
Eine Lösung ist z.B. Ψ = A ⋅ sin α x mit den Randbedingungen:<br />
Ψ<br />
Ψ<br />
( 0 ) = A ⋅ sin α ⋅ 0 = 0<br />
( a ) = A ⋅ sinα<br />
⋅ a = 0<br />
⇒<br />
[ n = 0, ± 1, 2, ...] "Quantenzahl".<br />
αa = nπ<br />
±<br />
Negative n können nicht zugelassen werden, da α ⋅ a positiv ist. n = 0 muß<br />
ausgeschlossen sein, da dann Ψ überall Null wäre.<br />
E<br />
n π<br />
= h<br />
2<br />
2ma<br />
α ⋅ a = n π n = 1,2,3...<br />
2 2 2<br />
2<br />
2 h<br />
n = n<br />
n =<br />
2<br />
8ma<br />
Die zugehörigen normierten Eigenfunktionen sind:<br />
1,2,3...<br />
Ψ<br />
n<br />
=<br />
2<br />
a<br />
n π<br />
⋅ sin<br />
a<br />
x<br />
mit<br />
2 als Normierungsfaktor.<br />
a<br />
http://www.chemgapedia.de/vsengine/supplement/Vlu/vsc/de/ch/13/vlu/praktik<br />
um1/farbe.vlu/Page/vsc/de/ch/13/pc/praktikum1/farbe/grundlagen_1_2.vscml/F<br />
ragment/459acdee659d2c35e1e7dbb8de57bee3-169.html
Wellenfunktionen<br />
Aufenthaltswahrscheinlichkeiten<br />
(pro Volumenelement)<br />
Hinweis: Knotensatz für das <strong>Teilchen</strong> <strong>im</strong> eind<strong>im</strong>ensionalen <strong>Kasten</strong>.<br />
Die Zahl der ″Knoten″ (Nulldurchgänge) einer Wellenfunktion ist um eins kleiner<br />
als die Quantenzahl des zugehörigen Energieeigenwertes.<br />
6.2 Der dreid<strong>im</strong>ensionale <strong>Kasten</strong><br />
∂<br />
2<br />
∂ x<br />
Ψ<br />
2<br />
+<br />
∂<br />
2<br />
∂ y<br />
Ψ<br />
2<br />
+<br />
∂<br />
2<br />
∂ z<br />
Ψ<br />
2<br />
2mE<br />
= −<br />
2<br />
h<br />
Ψ<br />
Variablenseparation:<br />
Ψ<br />
( x,<br />
y,z) = X( x) ⋅ Y( y) ⋅ Z( z)<br />
→<br />
einsetzen und durch X⋅Y⋅Z teilen:<br />
2<br />
2<br />
1 ∂ X 1 ∂ Y 1 ∂ Z 2mE<br />
⋅ + ⋅ + ⋅ = − .<br />
X<br />
2<br />
Y<br />
2<br />
Z<br />
2 2<br />
∂ x ∂ y ∂ z h<br />
2
Da diese Gleichung für alle Werte von X, Y, Z gilt, müssen die drei Summanden<br />
auf der linken Seite jeweils konstant sein:<br />
1<br />
X<br />
⋅<br />
∂<br />
2<br />
∂ x<br />
X<br />
2<br />
=<br />
−<br />
α<br />
2<br />
x<br />
1<br />
Y<br />
⋅<br />
∂<br />
2<br />
∂ y<br />
Y<br />
2<br />
=<br />
−<br />
α<br />
2<br />
y<br />
1<br />
Z<br />
⋅<br />
∂<br />
2<br />
∂ z<br />
Z<br />
2<br />
=<br />
−<br />
α<br />
2<br />
z<br />
mit<br />
2 2 2 2 2m E<br />
= α + α + α =<br />
x y z 2<br />
α .<br />
h<br />
Analog zum eind<strong>im</strong>ensionalen Potentialkasten erhält man:<br />
α<br />
x<br />
=<br />
1 π<br />
a<br />
n 2 π<br />
b<br />
n π<br />
c<br />
n 3<br />
α y =<br />
αz<br />
=<br />
n π<br />
a<br />
1<br />
( x) = A sin x n 1,2,3...<br />
X x 1 =<br />
n π<br />
b<br />
2<br />
( y) = A sin y n 1,2,3...<br />
Y y 2 =<br />
n π<br />
c<br />
3<br />
( z) = A sin y n 1,2,3...<br />
Z z 3 =<br />
n1<br />
πx<br />
n 2 π y n3<br />
πz<br />
Ψ n1<br />
n 2 n3<br />
( x, y,z)<br />
= Asin ⋅ sin ⋅ sin<br />
a b c<br />
Normierungskonstante<br />
A =<br />
8<br />
a bc<br />
E n1<br />
n<br />
2<br />
n<br />
3<br />
=<br />
h2<br />
α<br />
2m<br />
2<br />
=<br />
2<br />
8 h m<br />
⎛<br />
⎜<br />
⎝<br />
n<br />
a<br />
2<br />
1<br />
2<br />
+<br />
n<br />
b<br />
2<br />
2<br />
2<br />
+<br />
n<br />
c<br />
2<br />
3<br />
2<br />
⎞<br />
⎟<br />
⎠<br />
.
Zustandsdichte in einem <strong>Kasten</strong> mit a = b = c = L:<br />
E n1 n2n3<br />
=<br />
2 2 2<br />
( n + n + n )<br />
1<br />
1<br />
8mL<br />
Stellt man sich vor, dass die Quantenzahlen n einen Raum aufspannen, und dass<br />
ein Satz von n-Werten einen Punkt in diesem Raum darstellt, so kann man argumentieren,<br />
dass die mögliche Anzahl von Zuständen proportional zum "Volumen"<br />
des "n-Raums" ist.<br />
Hierzu wird der Radius R <strong>im</strong> „n-Raum“ definiert:<br />
2<br />
1<br />
h<br />
2<br />
R =<br />
2 2 2<br />
1 + n1<br />
n1<br />
n +<br />
Nun kann die Energie E durch R ausgedrückt werden:<br />
2 2mE<br />
R =<br />
h<br />
2<br />
2<br />
h R<br />
E =<br />
8mL<br />
2<br />
L<br />
Be<strong>im</strong> <strong>Teilchen</strong> <strong>im</strong> <strong>Kasten</strong> können <strong>im</strong> n-Raum nur positive Werte für n auftreten,<br />
daher muss das Volumen durch 8 geteilt werden. Da aber zwei verschiedene<br />
Spinwerte für das Elektron möglich sind, muss mit 2 multipliziert werden. Die<br />
Anzahl der Werte lautet dann:<br />
N =<br />
⎛ 1 ⎞ 4<br />
⎝ 8 ⎠ 3<br />
⎛ 8π<br />
⎞<br />
⎟<br />
⎝ 3 ⎠<br />
3<br />
2<br />
( 2) ⎜ ⎟ πR<br />
= ⎜ ( 2mE) 3 /<br />
3<br />
und die Anzahl der Zustände pro Volumen:<br />
3<br />
L<br />
h<br />
n<br />
z<br />
=<br />
N<br />
3<br />
L<br />
⎛ 8π<br />
⎞<br />
= ⎜ ⎟<br />
⎝ 3 ⎠<br />
( 2mE)<br />
h<br />
3<br />
3/ 2<br />
Die Zustandsdichte als Funktion der Energie ist die Ableitung von n z nach der<br />
Energie:<br />
dn z<br />
ρ E) =<br />
dE<br />
4π<br />
=<br />
( 2m)<br />
(<br />
3<br />
h<br />
3 / 2<br />
E
Ein Beispiel für den eind<strong>im</strong>ensionalen Potentialkasten: Hexatrien<br />
Es wird angenommen, daß die sechs π-Elektronen entlang des Moleküls frei<br />
beweglich sind (1-d<strong>im</strong>ensionales Potential):<br />
E<br />
=<br />
n<br />
2<br />
⋅ 8,02 ⋅ 10<br />
−18<br />
J<br />
n<br />
= 1,2,3...<br />
Jedes Energieniveau wird mit zwei Elektronen besetzt (Pauli-Prinzip).<br />
λ exp = 268nm
6.3 Der Tunneleffekt<br />
Eind<strong>im</strong>ensionaler Potentialkasten mit endlich hohen Wänden:<br />
In der klassischen Mechanik ist für E < V 0 dem <strong>Teilchen</strong> nur der Aufenthalt<br />
zwischen x = 0 und x = a erlaubt. In der Quantenmechanik existiert eine gewisse<br />
Aufenthaltswahrscheinlichkeit außerhalb des Bereiches [x, a] (″Tunneleffekt″),<br />
wenn die Potentialwände eine endliche Höhe haben.<br />
Hat eine Potentialbarriere eine endliche Breite, so kann die Materiewelle die<br />
Barriere durchdringen, auch wenn ihre Energie E n kleiner als V 0 ist.
Die Schrödingergleichung <strong>im</strong> Bereich der Barriere ist:<br />
2<br />
−h<br />
2m<br />
e<br />
⋅<br />
∂<br />
2<br />
∂ x<br />
Ψ<br />
2<br />
+<br />
V<br />
0<br />
Ψ<br />
=<br />
E Ψ<br />
∂<br />
2<br />
∂ x<br />
Ψ<br />
2<br />
=<br />
2m<br />
h<br />
e<br />
2<br />
( V − E) Ψ<br />
0<br />
2 m<br />
−<br />
e<br />
( V0<br />
− E) ⋅ x<br />
2<br />
Ψ(x)<br />
= A ⋅ e<br />
h<br />
.<br />
Die Wellenfunktion fällt also innerhalb der Barriere für E