Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ...
Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ... Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ...
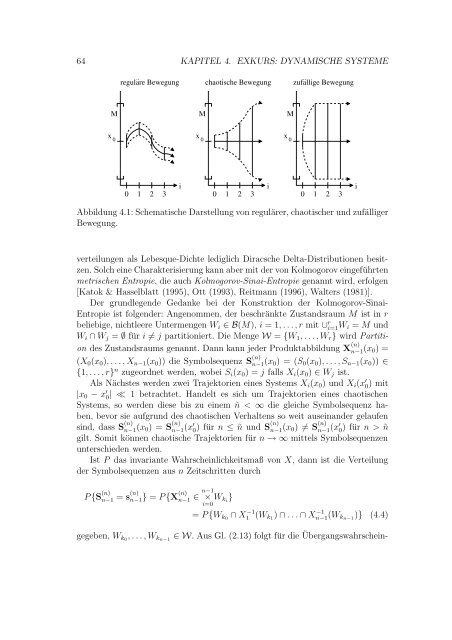
64 KAPITEL 4. EXKURS: DYNAMISCHE SYSTEME .. .. regulare Bewegung chaotische Bewegung zufallige Bewegung M M M x 0 x 0 x 0 i i 0 1 2 3 0 1 2 3 0 1 2 3 i Abbildung 4.1: Schematische Darstellung von regulärer, chaotischer und zufälliger Bewegung. verteilungen als Lebesque-Dichte lediglich Diracsche Delta-Distributionen besitzen. Solch eine Charakterisierung kann aber mit der von Kolmogorov eingeführten metrischen Entropie, die auch Kolmogorov-Sinai-Entropie genannt wird, erfolgen [Katok & Hasselblatt (1995), Ott (1993), Reitmann (1996), Walters (1981)]. Der grundlegende Gedanke bei der Konstruktion der Kolmogorov-Sinai- Entropie ist folgender: Angenommen, der beschränkte Zustandsraum M ist in r beliebige, nichtleere Untermengen W i ∈ B(M), i = 1, . . . , r mit ∪ r i=1 W i = M und W i ∩ W j = ∅ für i ≠ j partitioniert. Die Menge W = {W 1 , . . . , W r } wird Partition des Zustandsraums genannt. Dann kann jeder Produktabbildung X (n) n−1 (x 0) = (X 0 (x 0 ), . . . , X n−1 (x 0 )) die Symbolsequenz S (n) n−1(x 0 ) = (S 0 (x 0 ), . . . , S n−1 (x 0 )) ∈ {1, . . . , r} n zugeordnet werden, wobei S i (x 0 ) = j falls X i (x 0 ) ∈ W j ist. Als Nächstes werden zwei Trajektorien eines Systems X i (x 0 ) und X i (x ′ 0) mit |x 0 − x ′ 0 | ≪ 1 betrachtet. Handelt es sich um Trajektorien eines chaotischen Systems, so werden diese bis zu einem ñ < ∞ die gleiche Symbolsequenz haben, bevor sie aufgrund des chaotischen Verhaltens so weit auseinander gelaufen sind, dass S (n) n−1 (x 0) = S (n) n−1 (x′ 0 ) für n ≤ ñ und S(n) n−1 (x 0) ≠ S (n) n−1 (x′ 0 ) für n > ñ gilt. Somit können chaotische Trajektorien für n → ∞ mittels Symbolsequenzen unterschieden werden. Ist P das invariante Wahrscheinlichkeitsmaß von X, dann ist die Verteilung der Symbolsequenzen aus n Zeitschritten durch P {S (n) n−1 = s (n) n−1} = P {X (n) n−1 ∈ n−1 × i=0 W ki } = P {W k0 ∩ X −1 1 (W k 1 ) ∩ . . . ∩ X −1 n−1 (W k n−1 )} (4.4) gegeben, W k0 , . . . , W kn−1 ∈ W. Aus Gl. (2.13) folgt für die Übergangswahrschein-
4.1. ENTROPIE EINES DYNAMISCHEN SYSTEMS 65 lichkeit, mit der X n in einem Partitionselement W kn zu finden ist, P {X n ∈ W kn |X (n) n−1 ∈ n−1 × i=0 W ki } = P {X n ∈ W kn |W k0 ∩ X −1 1 (W k 1 ) ∩ . . . ∩ X −1 n−1 (W k n−1 )} = P {W k 0 ∩ X1 −1 (W k1 ) ∩ . . . ∩ Xn−1(W kn−1 ) ∩ Xn −1 (W kn )} P {W 0 ∩ X1 −1 (W k1 ) ∩ . . . ∩ Xn−1(W kn−1 )} . (4.5) Werden diese Wahrscheinlichkeiten in die bedingte Shannon-Entropie, Gl. (2.15), eingesetzt, wobei jetzt über die Partitionselemente zu summieren ist, so erhält man die mittlere Unsicherheit, mit der die zukünftigen Zustände bezüglich der Partitionierung des Zustandsraums bei bekannter Vergangenheit beobachtet werden. Diese diskretisierte bedingte Shannon-Entropie wird mit H W;P (X n |X (n) n−1 ) bezeichnet. Nach dem oben Gesagten lassen sich in einem chaotischen System die Trajektorien und damit deren Anfangswerte X 0 (x 0 ) = x 0 umso besser unterscheiden, je mehr Zeitbeobachtungen vorliegen. Da andererseits die Systemzustände X n durch x 0 eindeutig bestimmt sind, folgt hieraus, dass für große n die Entropie H W;P (X n |X (n) n−1) konvergiert: h(W; P ) = lim n→∞ H W;P (X n |X (n) n−1) . (4.6) Dieser Grenzwert hängt von der Partition W und dem invarianten Maß P ab. Letzteres ist für die hier betrachteten dynamischen Systeme eindeutig bestimmt, so dass nur noch die Willkürlichkeit der Partitionswahl beseitigt werden muss. Hierzu wird das Supremum von h(W; P ) über alle Partitionen W genommen, h KS (P ) = sup h(W; P ) . (4.7) W Diese Größe wird Kolmogorov-Sinai-Entropie genannt. Sie charakterisiert die Unsicherheit, mit der die Trajektorie eines dynamischen Systems identifiziert werden kann, wenn das System zu beliebig vielen Zeitpunkten beobachtet wird und wenn eine beliebig genaue Messauflösung zur Verfügung steht. Entsprechend Gl. (2.16) kann die diskretisierte bedingte Shannon-Entropie als Differenz von Shannon-Entropien geschreiben werden, H W;P (X n |X n−1) (n) = H W;P (X (n+1) ) − H W;P (X (n) n−1) . Die Shannon-Entropien lassen sich als Unsicherheiten bei der Identifikation der Trajektorien interpretieren. Da andererseits die Trajektorien durch ihre Anfangswerte x 0 festgelegt sind, ist H W;P (X n |X (n) n−1) der Verlust von Unsicherheit über den Anfangswert, wenn das dynamische System zu einem späteren Zeitpunkt ein n
- Seite 19 und 20: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 21 und 22: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 23 und 24: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 25 und 26: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 27 und 28: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 29 und 30: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 31 und 32: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 33 und 34: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 35 und 36: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 37 und 38: Kapitel 3 Schätzen von Entropien u
- Seite 39 und 40: 3.1. SCHÄTZEN BEI EINER UND MEHRER
- Seite 41 und 42: 3.2. SCHÄTZER FÜR DISKRETE PROZES
- Seite 43 und 44: 3.3. PARTITIONIERUNG DES ZUSTANDSRA
- Seite 45 und 46: 3.3. PARTITIONIERUNG DES ZUSTANDSRA
- Seite 47 und 48: 3.3. PARTITIONIERUNG DES ZUSTANDSRA
- Seite 49 und 50: 3.4. PARAMETRISCHE VERTEILUNGEN 43
- Seite 51 und 52: 3.5. KONTINUIERLICHES BEISPIEL: AR(
- Seite 53 und 54: 3.6. KERNSCHÄTZER FÜR DICHTEN 47
- Seite 55 und 56: 3.6. KERNSCHÄTZER FÜR DICHTEN 49
- Seite 57 und 58: 3.6. KERNSCHÄTZER FÜR DICHTEN 51
- Seite 59 und 60: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 61 und 62: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 63 und 64: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 65 und 66: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 67 und 68: Kapitel 4 Exkurs: Dynamische System
- Seite 69: 4.1. ENTROPIE EINES DYNAMISCHEN SYS
- Seite 73 und 74: 4.2. INTERDEPENDENZ, VERALLGEMEINER
- Seite 75 und 76: 4.2. INTERDEPENDENZ, VERALLGEMEINER
- Seite 77 und 78: 4.2. INTERDEPENDENZ, VERALLGEMEINER
- Seite 79 und 80: Kapitel 5 Punktprozesse 5.1 Definit
- Seite 81 und 82: 5.1. DEFINITION EINES PUNKTPROZESSE
- Seite 83 und 84: 5.2. MOMENTE UND EREIGNISRATEN 77 2
- Seite 85 und 86: 5.3. GEKOPPELTE PUNKTPROZESSE 79 Be
- Seite 87 und 88: 5.3. GEKOPPELTE PUNKTPROZESSE 81 f
- Seite 89 und 90: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 91 und 92: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 93 und 94: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 95 und 96: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 97 und 98: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 99 und 100: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 101 und 102: 5.5. NACHWEIS VON KOPPLUNG MITTELS
- Seite 103 und 104: 5.5. NACHWEIS VON KOPPLUNG MITTELS
- Seite 105 und 106: 5.5. NACHWEIS VON KOPPLUNG MITTELS
- Seite 107 und 108: 5.5. NACHWEIS VON KOPPLUNG MITTELS
- Seite 109 und 110: 5.6. ABHÄNGIGKEITSNACHWEIS ÜBER E
- Seite 111 und 112: 5.6. ABHÄNGIGKEITSNACHWEIS ÜBER E
- Seite 113 und 114: 5.6. ABHÄNGIGKEITSNACHWEIS ÜBER E
- Seite 115 und 116: Kapitel 6 Zusammenfassung Die Besti
- Seite 117 und 118: 111 zwischen zwei Prozessen nachgew
- Seite 119 und 120: Anhang A Mathematische Werkzeuge De
64 KAPITEL 4. EXKURS: DYNAMISCHE SYSTEME<br />
..<br />
..<br />
regulare Bewegung chaotische Bewegung zufallige Bewegung<br />
M<br />
M<br />
M<br />
x<br />
0<br />
x 0<br />
x 0<br />
i<br />
i<br />
0 1 2 3 0 1 2 3 0 1 2<br />
3<br />
i<br />
Abbildung 4.1: Schematische Darstellung <strong>von</strong> regulärer, chaotischer <strong>und</strong> zufälliger<br />
Bewegung.<br />
verteilungen als Lebesque-Dichte lediglich Diracsche Delta-Distributionen besitzen.<br />
Solch eine Charakterisierung kann aber mit der <strong>von</strong> Kolmogorov eingeführten<br />
metrischen Entropie, die auch Kolmogorov-Sinai-Entropie genannt wird, erfolgen<br />
[Katok & Hasselblatt (1995), Ott (1993), Reitmann (1996), Walters (1981)].<br />
Der gr<strong>und</strong>legende Gedanke bei der Konstruktion der Kolmogorov-Sinai-<br />
Entropie ist folgender: Angenommen, der beschränkte Zustandsraum M ist in r<br />
beliebige, nichtleere Untermengen W i ∈ B(M), i = 1, . . . , r mit ∪ r i=1 W i = M <strong>und</strong><br />
W i ∩ W j = ∅ für i ≠ j partitioniert. Die Menge W = {W 1 , . . . , W r } wird Partition<br />
des Zustandsraums genannt. Dann kann jeder Produktabbildung X (n)<br />
n−1 (x 0) =<br />
(X 0 (x 0 ), . . . , X n−1 (x 0 )) die Symbolsequenz S (n)<br />
n−1(x 0 ) = (S 0 (x 0 ), . . . , S n−1 (x 0 )) ∈<br />
{1, . . . , r} n zugeordnet werden, wobei S i (x 0 ) = j falls X i (x 0 ) ∈ W j ist.<br />
Als Nächstes werden zwei Trajektorien eines Systems X i (x 0 ) <strong>und</strong> X i (x ′ 0) mit<br />
|x 0 − x ′ 0 | ≪ 1 betrachtet. Handelt es sich um Trajektorien eines chaotischen<br />
Systems, so werden diese bis zu einem ñ < ∞ die gleiche Symbolsequenz haben,<br />
bevor sie aufgr<strong>und</strong> des chaotischen Verhaltens so weit auseinander gelaufen<br />
sind, dass S (n)<br />
n−1 (x 0) = S (n)<br />
n−1 (x′ 0 ) für n ≤ ñ <strong>und</strong> S(n) n−1 (x 0) ≠ S (n)<br />
n−1 (x′ 0 ) für n > ñ<br />
gilt. Somit können chaotische Trajektorien für n → ∞ mittels Symbolsequenzen<br />
unterschieden werden.<br />
Ist P das invariante Wahrscheinlichkeitsmaß <strong>von</strong> X, dann ist die Verteilung<br />
der Symbolsequenzen aus n Zeitschritten durch<br />
P {S (n)<br />
n−1 = s (n)<br />
n−1} = P {X (n)<br />
n−1 ∈ n−1<br />
×<br />
i=0<br />
W ki }<br />
= P {W k0 ∩ X −1<br />
1 (W k 1<br />
) ∩ . . . ∩ X −1<br />
n−1 (W k n−1<br />
)} (4.4)<br />
gegeben, W k0 , . . . , W kn−1 ∈ W. Aus Gl. (2.13) folgt für die Übergangswahrschein-