Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ...
Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ... Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ...
50 KAPITEL 3. SCHÄTZEN VON ENTROPIEN UND INFORMATIONEN Gl. (2.10) bzw. Gl. (2.27) angewendet, wobei in den beiden letztgenannten Arbeiten das gleiche Prinzip aber eine anderen Korrektur verwendet wurde. Diese Vorgehensweise birgt aber einen zusätzlichen nachteiligen Effekt in sich, denn die Fluktuationen zum Beispiel in g X (k) i sind aufgrund endlicher und g ,Y (l) j ;ε X (k) i ;ε Daten nicht unabhängig voneinander, weshalb deren Bias nicht separat voneinander korrigiert werden dürfen. Wie sich herausstellte, ist die Auswirkung dieses Effektes bei der Biaskorrektur sogar noch sehr viel problematischer als der Bias aufgrund der Fluktuationen selbst. Da keine geeignete Korrektur zur Verfügung steht, werden die unkorrigierten Schätzer verwendet. Zusätzlich werden in der Summe von Gl. (3.35) und Gl. (3.37) all jene Terme Null gesetzt, bei denen weniger als n min Punkte zum Schätzen der Dichte zur Verfügung stehen, das heißt es wird angenommen, dass die Dichten in diesem Fall lokal faktorisieren. Hierdurch werden die lokalen Fluktuationen der Kernschätzer reduziert, dafür tritt bei kleinen Bandbreiten ein Bias in Richtung Null auf. Die Anwendung der Kernschätzer soll an einem Beispiel demonstriert werden. Hierzu wird das in Absch. 3.5, Gl. (3.29) vorgestellte System von gekoppelten autoregressiven Prozessen verwendet, wobei diesmal der Kopplungsparameter mit c = 0.4 fest gewählt wird. Zum Schätzen der Dichten werden Rechteckkerne mit gleicher Bandbreite für beide Signale und alle Komponenten verwendet. Die Zeitreihe hat eine Länge von 10 000 Punkten. Das Theilerfenster w wurde gleich 20 gewählt. Wie sich herausstellte, erhält man die robustesten Resultate mit n min = 4. In Abb. 3.4 sind die gegenseitigen Information ˆM ε (X i+1 , Y i ) und ˆM ε (Y i+1 , X i ) als auch die Transferentropien ˆT ε (X i+1 |X i , Y i ) und ˆT ε (Y i+1 |Y i , X i ) über die Bandbreite ε aufgetragen. Mit abnehmender Bandbreite erreichen alle Kurven ein Plateau nahe am theoretischen Wert. Am unteren Ende setzen Fluktuationen aufgrund endlich vieler Datenpunkte ein. Dies ist für die Transferentropie ˆT ε (X i+1 |X i , Y i ) stärker ausgeprägt, was damit zusammenhängt, dass hier bereits Dichten auf dem R 3 zu schätzen sind. Der theoretische Wert von 0.0923 wird von ˆT ε (X i+1 |X i , Y i ) nicht erreicht (durchgezogene Linie). Über eine große Skalenbreite hingegen liefert ˆT ε (Y i+1 |Y i , X i ) innerhalb statistischer Fluktuationen einen Wert von 0. Die Verwendung von parabolischen Kernen lieferte, obwohl sie eine kleinere Varianz als rechteckige Kerne haben [Silverman (1986)], lediglich für ˆM ε (X i+1 , Y i ) ein geringfügig stärker ausgeprägtes Plateau. Für die anderen Größen hingegen waren die Plateaus deutlich schlechter ausgeprägt als in Abb. 3.4, bzw. existierten noch nicht einmal. Insbesondere ist hier die Unterdrückung der Fluktuationen mit n min nicht so effektiv wie bei den rechteckigen Kernen. Bei den hier verwendeten Schätzern wurde die Bandbreite ε fest gewählt und anschließend die Anzahl der Nachbarn gezählt, die in der durch ε festgelegten Umgebung um x i (n) liegen. Alternativ hierzu kann auch die Anzahl der Nachbarn
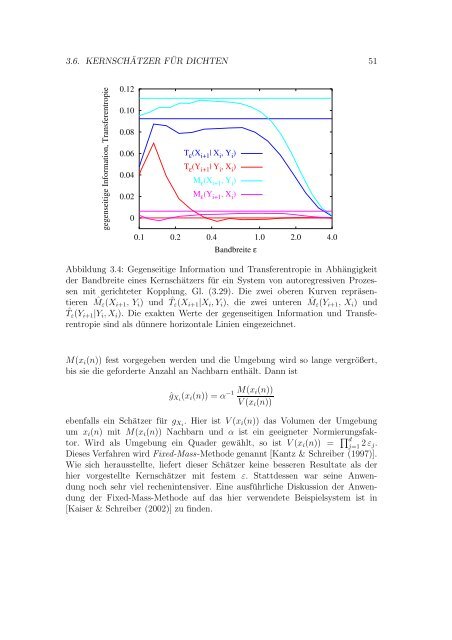
3.6. KERNSCHÄTZER FÜR DICHTEN 51 gegenseitige Information, Transferentropie 0.12 0.10 0.08 0.06 T ε (X i+1 | X i , Y i ) 0.04 T ε (Y i+1 | Y i , X i ) M ε (X i+1 , Y i ) 0.02 M ε (Y i+1 , X i ) 0 0.1 0.2 0.4 1.0 2.0 4.0 Bandbreite ε Abbildung 3.4: Gegenseitige Information und Transferentropie in Abhängigkeit der Bandbreite eines Kernschätzers für ein System von autoregressiven Prozessen mit gerichteter Kopplung, Gl. (3.29). Die zwei oberen Kurven repräsentieren ˆM ε (X i+1 , Y i ) und ˆT ε (X i+1 |X i , Y i ), die zwei unteren ˆM ε (Y i+1 , X i ) und ˆT ε (Y i+1 |Y i , X i ). Die exakten Werte der gegenseitigen Information und Transferentropie sind als dünnere horizontale Linien eingezeichnet. M(x i (n)) fest vorgegeben werden und die Umgebung wird so lange vergrößert, bis sie die geforderte Anzahl an Nachbarn enthält. Dann ist ĝ Xi (x i (n)) = α −1 M(x i(n)) V (x i (n)) ebenfalls ein Schätzer für g Xi . Hier ist V (x i (n)) das Volumen der Umgebung um x i (n) mit M(x i (n)) Nachbarn und α ist ein geeigneter Normierungsfaktor. Wird als Umgebung ein Quader gewählt, so ist V (x i (n)) = ∏ d j=1 2 ε j. Dieses Verfahren wird Fixed-Mass-Methode genannt [Kantz & Schreiber (1997)]. Wie sich herausstellte, liefert dieser Schätzer keine besseren Resultate als der hier vorgestellte Kernschätzer mit festem ε. Stattdessen war seine Anwendung noch sehr viel rechenintensiver. Eine ausführliche Diskussion der Anwendung der Fixed-Mass-Methode auf das hier verwendete Beispielsystem ist in [Kaiser & Schreiber (2002)] zu finden.
- Seite 5 und 6: Inhaltsverzeichnis 1 Einleitung 1 2
- Seite 7 und 8: Kapitel 1 Einleitung Zum Verständn
- Seite 9 und 10: Sobald kontinuierliche Prozesse bet
- Seite 11 und 12: Kapitel 2 Grundlagen der Informatio
- Seite 13 und 14: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 15 und 16: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 17 und 18: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 19 und 20: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 21 und 22: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 23 und 24: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 25 und 26: 2.1. DISKRETE STOCHASTISCHE PROZESS
- Seite 27 und 28: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 29 und 30: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 31 und 32: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 33 und 34: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 35 und 36: 2.2. KONTINUIERLICHE STOCHASTISCHE
- Seite 37 und 38: Kapitel 3 Schätzen von Entropien u
- Seite 39 und 40: 3.1. SCHÄTZEN BEI EINER UND MEHRER
- Seite 41 und 42: 3.2. SCHÄTZER FÜR DISKRETE PROZES
- Seite 43 und 44: 3.3. PARTITIONIERUNG DES ZUSTANDSRA
- Seite 45 und 46: 3.3. PARTITIONIERUNG DES ZUSTANDSRA
- Seite 47 und 48: 3.3. PARTITIONIERUNG DES ZUSTANDSRA
- Seite 49 und 50: 3.4. PARAMETRISCHE VERTEILUNGEN 43
- Seite 51 und 52: 3.5. KONTINUIERLICHES BEISPIEL: AR(
- Seite 53 und 54: 3.6. KERNSCHÄTZER FÜR DICHTEN 47
- Seite 55: 3.6. KERNSCHÄTZER FÜR DICHTEN 49
- Seite 59 und 60: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 61 und 62: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 63 und 64: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 65 und 66: 3.7. RÄUMLICHE ABHÄNGIGKEIT DES W
- Seite 67 und 68: Kapitel 4 Exkurs: Dynamische System
- Seite 69 und 70: 4.1. ENTROPIE EINES DYNAMISCHEN SYS
- Seite 71 und 72: 4.1. ENTROPIE EINES DYNAMISCHEN SYS
- Seite 73 und 74: 4.2. INTERDEPENDENZ, VERALLGEMEINER
- Seite 75 und 76: 4.2. INTERDEPENDENZ, VERALLGEMEINER
- Seite 77 und 78: 4.2. INTERDEPENDENZ, VERALLGEMEINER
- Seite 79 und 80: Kapitel 5 Punktprozesse 5.1 Definit
- Seite 81 und 82: 5.1. DEFINITION EINES PUNKTPROZESSE
- Seite 83 und 84: 5.2. MOMENTE UND EREIGNISRATEN 77 2
- Seite 85 und 86: 5.3. GEKOPPELTE PUNKTPROZESSE 79 Be
- Seite 87 und 88: 5.3. GEKOPPELTE PUNKTPROZESSE 81 f
- Seite 89 und 90: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 91 und 92: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 93 und 94: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 95 und 96: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 97 und 98: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 99 und 100: 5.4. NACHWEIS VON ABHÄNGIGKEITEN M
- Seite 101 und 102: 5.5. NACHWEIS VON KOPPLUNG MITTELS
- Seite 103 und 104: 5.5. NACHWEIS VON KOPPLUNG MITTELS
- Seite 105 und 106: 5.5. NACHWEIS VON KOPPLUNG MITTELS
3.6. KERNSCHÄTZER FÜR DICHTEN 51<br />
gegenseitige Information, Transferentropie<br />
0.12<br />
0.10<br />
0.08<br />
0.06<br />
T ε (X i+1 | X i , Y i )<br />
0.04<br />
T ε (Y i+1 | Y i , X i )<br />
M ε (X i+1 , Y i )<br />
0.02<br />
M ε (Y i+1 , X i )<br />
0<br />
0.1 0.2 0.4 1.0 2.0 4.0<br />
Bandbreite ε<br />
Abbildung 3.4: Gegenseitige Information <strong>und</strong> Transferentropie in Abhängigkeit<br />
der Bandbreite eines Kernschätzers für ein System <strong>von</strong> autoregressiven Prozessen<br />
mit gerichteter Kopplung, Gl. (3.29). Die zwei oberen Kurven repräsentieren<br />
ˆM ε (X i+1 , Y i ) <strong>und</strong> ˆT ε (X i+1 |X i , Y i ), die zwei unteren ˆM ε (Y i+1 , X i ) <strong>und</strong><br />
ˆT ε (Y i+1 |Y i , X i ). Die exakten Werte der gegenseitigen Information <strong>und</strong> Transferentropie<br />
sind als dünnere horizontale Linien eingezeichnet.<br />
M(x i (n)) fest vorgegeben werden <strong>und</strong> die Umgebung wird so lange vergrößert,<br />
bis sie die geforderte Anzahl an Nachbarn enthält. Dann ist<br />
ĝ Xi (x i (n)) = α −1 M(x i(n))<br />
V (x i (n))<br />
ebenfalls ein Schätzer für g Xi . Hier ist V (x i (n)) das Volumen der Umgebung<br />
um x i (n) mit M(x i (n)) Nachbarn <strong>und</strong> α ist ein geeigneter Normierungsfaktor.<br />
Wird als Umgebung ein Quader gewählt, so ist V (x i (n)) = ∏ d<br />
j=1 2 ε j.<br />
Dieses Verfahren wird Fixed-Mass-Methode genannt [Kantz & Schreiber (1997)].<br />
Wie sich herausstellte, liefert dieser Schätzer keine besseren Resultate als der<br />
hier vorgestellte Kernschätzer mit festem ε. Stattdessen war seine Anwendung<br />
noch sehr viel rechenintensiver. Eine ausführliche Diskussion der Anwendung<br />
der Fixed-Mass-Methode auf das hier verwendete Beispielsystem ist in<br />
[Kaiser & Schreiber (2002)] zu finden.