Mathematik für Ingenieure I - Institut für Algebraische Geometrie ...

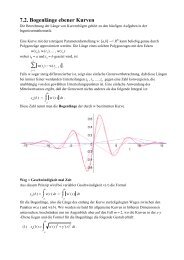
68 Kapitel 3. Funktionen
s n
Abbildung 3.2: Partialsummen einer alternierenden Reihe
0 1 2 3 4 5 6 7 8 9 10 n
Man leitet leicht die folgenden Rechenregeln für Werte von Reihen ab.
Satz 3.2.8 (Rechenregeln für Summen von Reihen) (1) Ist ∑ ∞
k=0 a k
und ∑ ∞
k=0 b k konvergent, so ist auch ∑ ∞
k=0 (a k + b k ) konvergent und es
gilt
∞∑
∞∑ ∞∑
(a k + b k ) = a k + b k .
k=0
k=0
k=0
(2) Ist ∑ ∞
k=0 a k konvergent und c ∈ R, so ist auch ∑ ∞
k=0 c · a k konvergent
und es gilt
∞∑
∞∑
c · a k = c · a k .
k=0
k=0
Warnung Eine Summe von endlich vielen Zahlen ist unabhängig von der
Reihenfolge. Bei einer Reihe kann jedoch das Umordnen der Glieder zu seltsamen
Resultaten führen: Wir betrachten wieder die alternierende Reihe
∞∑
(−1) k+1 1 k .
k=1
Nach dem Leibnizkriterium konvergiert diese Reihe gegen eine Zahl s. Wir