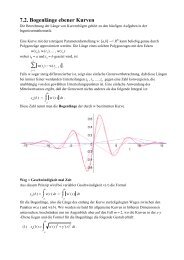
Mathematik für Ingenieure I - Institut für Algebraische Geometrie ...

1.2 Der Vektorraum R n 5
Zwischen den bisher genannten Mengen hat man die folgenden Teilmengenbeziehungen:
N ⊆ Z ⊆ Q ⊆ R.
1.2 Der Vektorraum R n
Wir stellen uns die reellen Zahlen als Zahlengerade vor. Jedem Punkt der
Geraden entspricht eine reelle Zahl. Jedem Punkt der Ebene entspricht ein
Paar (x, y), jedem Punkt des Raumes ein Tripel (x, y, z) von reellen Zahlen.
Allgemein nennt man
(x 1 , x 2 , . . . , x n ), wobei x 1 , . . . , x n reelle Zahlen sind,
ein n-Tupel (n ist hierbei eine beliebige natürliche Zahl). Wir setzen
R n := {⃗x = (x 1 , . . . , x n ) | x 1 , . . . , x n ∈ R}.
Man beachte, dass bei einem n-Tupel die Reihenfolge wichtig ist, d.h. zwei Tupel
(x 1 , . . . , x n ) und (y 1 , . . . , y n ) sind genau dann gleich, wenn x 1 = y 1 , . . . , x n =
y n . Man nennt den R n auch den reellen Standardvektorraum der Dimension
n und ein Element dieses Raumes auch einen Vektor. Die Zahlen x 1 , . . . , x n
heissen die Komponenten von ⃗x.
Der R 1 ist die Zahlengerade, R 2 entspricht der Ebene, R 3 dem Raum. Für
größere n hat man keine geometrische Vorstellung mehr.
Mit den reellen Zahlen kann man rechnen, man kann sie nach den üblichen
Regeln addieren und multiplizieren. Auch mit n-Tupeln kann man rechnen.
Für (x 1 , . . . , x n ) ∈ R n und (y 1 , . . . , y n ) ∈ R n definieren wir eine Addition
(x 1 , . . . , x n ) + (y 1 , . . . , y n ) := (x 1 + y 1 , . . . , x n + y n )
und für (x 1 , . . . , x n ) ∈ R n eine Multiplikation mit einer Zahl λ ∈ R
Wir setzen ausserdem:
λ(x 1 , . . . , x n ) := (λx 1 , . . . , λx n ).
⃗0 := (0, . . . , 0)
−⃗x := (−x 1 , . . . , −x n ).
Statt ⃗x + (−⃗y) schreibt man kürzer ⃗x − ⃗y.
Man kann diese Operationen geometrisch deuten: Dazu sehen wir ein n-
Tupel ⃗x = (x 1 , . . . , x n ) als Vektor an, d.h. als einen Pfeil mit Fußpunkt in