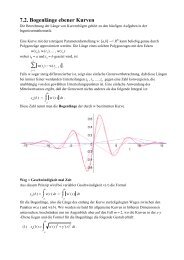
Mathematik für Ingenieure I - Institut für Algebraische Geometrie ...

4 Kapitel 1. Lineare Algebra I
Um nun einen Punkt für die rationale Zahl p , p, q ∈ Z, q > 0, festzulegen,
q
teilt man die Strecke 0p auf der Geraden in q gleiche Teile. Der am dichtesten
bei 0 gelegene Teilpunkt steht dann für p . q
q = 5 gleiche Teile
p = −4
p
q = − 4 5
0 1
Man sieht dann ein, dass die rationalen Zahlen ”dicht” auf der Geraden
liegen. Das heißt, in jeder noch so kleinen Umgebung eines jeden Punktes
der Geraden findet man eine rationale Zahl (genauer gesagt, einen Punkt,
der eine rationale Zahl repräsentiert). Um einen solchen Punkt zu finden,
muss man q genügend groß und p passend wählen.
Allerdings hat man bisher keineswegs alle Punkte der Geraden erwischt.
Die Diagonale des Einheitsquadrats hat die Länge √ 2.
0 1 2
❅
❅
❅
√
2
Satz 1.1.1 Die Zahl √ 2 ist irrational (d.h. nicht rational).
Beweis. Dieser Beweis ist ein Beispiel für einen indirekten Beweis. Wir nehmen an, dass
√
2 rational ist, und leiten daraus einen Widerspruch her. Wir nehmen also an
√ p 2 = , p, q ∈ Z, q ≠ 0.
q
Ohne Einschränkung können wir zusätzlich annehmen, dass dieser Bruch bereits gekürzt
ist. Insbesondere können wir annehmen, dass p und q nicht beide gerade sind.
Aus √ 2 = p q folgt aber 2q 2 = p 2 .
Daraus folgt p 2 gerade. Da aber Quadrate ungerader Zahlen wieder ungerade sind, muss
also schon p gerade sein, d.h. p = 2p ′ für ein p ′ ∈ Z. Setzen wir dies für p in die obige
Gleichung ein, so folgt
2q 2 = 4(p ′ ) 2 .
Teilen wir beide Seiten der Gleichung durch 2, so erhalten wir
q 2 = 2(p ′ ) 2 .
Daraus folgt nun aber, dass auch q 2 und damit q gerade sein muss. Dies ist aber ein
Widerspruch zu unserer Annahme. Also war unsere Annahme, dass √ 2 rational ist, falsch.
✷