Korrektur: Lineare Regression in Excel ... - BayCEER
Korrektur: Lineare Regression in Excel ... - BayCEER
Korrektur: Lineare Regression in Excel ... - BayCEER
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
<strong>Korrektur</strong>: <strong>L<strong>in</strong>eare</strong> <strong>Regression</strong> <strong>in</strong> <strong>Excel</strong><br />
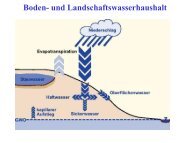
Doppelsummenkurve<br />
10000<br />
8000<br />
kum. Abfluss<br />
6000<br />
4000<br />
2000<br />
Juni 1987<br />
0<br />
0 5000 10000 15000 20000<br />
kum. Niederschlag<br />
1
PDFA Abfluss Lange Bramke<br />
400<br />
kum. Stabw.<br />
300<br />
200<br />
100<br />
Feb. 1981<br />
0<br />
01.80 01.82 01.84 01.86 01.88 01.90 01.92 01.94 01.96<br />
Zum Vergleich: Wiederkehrdiagramm<br />
1993<br />
1992<br />
1991<br />
1990<br />
1989<br />
1988<br />
1987<br />
1986<br />
1985<br />
1984<br />
1983<br />
1982<br />
1981<br />
1980<br />
1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993<br />
2
Zeitreihen<br />
120<br />
100<br />
100<br />
80<br />
60<br />
80<br />
60<br />
40<br />
20<br />
0<br />
Niederschlag<br />
-20<br />
Abfluss<br />
40<br />
20<br />
-40<br />
-60<br />
-80<br />
0<br />
-100<br />
01.01.80 01.01.82 01.01.84 01.01.86 01.01.88 01.01.90 01.01.92 01.01.94<br />
PDFA Niederschlag und Temperatur<br />
Niederschlag<br />
Temperatur<br />
1200<br />
600<br />
1000<br />
500<br />
kum. Stabw.<br />
800<br />
600<br />
400<br />
kum. Stabw.<br />
400<br />
300<br />
200<br />
200<br />
100<br />
0<br />
0<br />
01.80 01.82 01.84 01.86 01.88 01.90 01.92 01.94<br />
01.80 01.82 01.84 01.86 01.88 01.90 01.92 01.94<br />
3
Extremwerte<br />
Motivation: Oft s<strong>in</strong>d nicht Mittelwerte, sondern die Extrema von Interesse<br />
Fragestellung: Lässt sich aus der Verteilung der beobachteten (Jahres-)Maxima<br />
die Wahrsche<strong>in</strong>lichkeit extrem seltener Maxima (z.B. HQ 100<br />
) abschätzen?<br />
Problem: Extrema s<strong>in</strong>d sehr schwer zu schätzen<br />
- Spannweite der Werte steigt mit zunehmendem Stichprobenumfang<br />
(ke<strong>in</strong>e Sättigung der Statistik)<br />
- Kle<strong>in</strong>e Änderungen der Parametrisierungen angepasster<br />
Häufigkeitsverteilungen wirken sich sehr stark auf die Wahrsche<strong>in</strong>lichkeit<br />
der Extremwerte aus<br />
- Extrema s<strong>in</strong>d selten<br />
Zwei verschiedene Ansätze<br />
1. Block-Extrema (Fenster gleicher Länge; Bsp.: Jahresmaxima): GEV<br />
2. Schwellwertüberschreitungen (POT = Peak over Threshold): GPD<br />
4
Annahmen<br />
• Verteilung der x(t) ist nicht bekannt<br />
• unabhängige und gleichverteilte Maxima (i.i.d. = <strong>in</strong>dependent and<br />
identically distributed)<br />
• Extreme Ereignisse s<strong>in</strong>d unkorreliert: Asymptotic Independence<br />
of Maxima Theorem (AIM-Theorem)<br />
• Approximation für<br />
n → ∞<br />
Allgeme<strong>in</strong>e Extremwertverteilung<br />
(GEV = General Extreme Value Distribution)<br />
GEV<br />
ξ , x,<br />
σ<br />
- x:<br />
Mittelwert (Lageparameter)<br />
- σ: Standardabweichung (Skalenparameter)<br />
- ξ: Formparameter<br />
( x)<br />
=<br />
⎧<br />
⎪<br />
⎨e<br />
⎪<br />
⎩<br />
⎛<br />
⎜ ⎛ x−<br />
x ⎞<br />
− 1+<br />
ξ<br />
⎜ ⎟<br />
⎝ ⎝ σ ⎠<br />
−e<br />
−1/<br />
ξ<br />
⎛ x−x<br />
⎞<br />
−⎜<br />
⎟<br />
⎝ σ ⎠<br />
für ξ = 0: Exponential Tail (Gumbel-Verteilung)<br />
e<br />
⎞<br />
⎟<br />
⎠<br />
für ξ ≠ 0<br />
für ξ = 0<br />
für ξ > 0: Heavy Tail<br />
für ξ < 0: F<strong>in</strong>ite Tail<br />
(Fréchet-Verteilung)<br />
(neg. Weibull-Verteilung)<br />
5
GEV: 3 Typen<br />
0.7<br />
0.6<br />
Gumbel; ξ=0<br />
Fréchet; ξ=0,8<br />
Weibull; ξ=-0,8<br />
0.5<br />
pdf (GEV(x,0,1,ξ))<br />
0.4<br />
0.3<br />
0.2<br />
0.1<br />
0<br />
-6 -4 -2 0 2 4 6 8 10<br />
x<br />
(Endres 2005)<br />
Verallgeme<strong>in</strong>erte Pareto-Verteilung<br />
(GPD = Generalized Pareto Distribution)<br />
•für x‘ = Schwellwert:<br />
GPD<br />
′<br />
x−<br />
x′<br />
−1/<br />
ξ<br />
ξ , σ<br />
( x − x ) = 1−<br />
(1 + ξ ⋅ )<br />
σ<br />
•3 Spezialfälle:<br />
für ξ = 0: Exponential Tail (Exponential-Verteilung, GP0)<br />
für ξ > 0: Heavy Tail<br />
für ξ < 0: F<strong>in</strong>ite Tail<br />
(Pareto-Verteilung, GP1)<br />
(Beta-Verteilung, GP2)<br />
6
GPD: 3 Typen<br />
(Endres 2005)<br />
GEV vs. GPD<br />
• Zusammenhang:<br />
GPD( x)<br />
= 1+<br />
logGEV<br />
( x)<br />
für logGEV<br />
( x)<br />
> −1<br />
• Ausnutzung der Daten:<br />
- bestimmt durch Fensterlänge (GEV) oder Schwellwert (GPD);<br />
- jeweils so zu wählen, dass die Extrema vone<strong>in</strong>ander unabhängig s<strong>in</strong>d<br />
• Präferenzen:<br />
- Kont<strong>in</strong>uierliche Messungen: GEV, z.B. Abflussgangl<strong>in</strong>ien<br />
- Protokollierung der Extremereignisse: GPD, z.B. Schadensmeldungen der<br />
Versicherungen<br />
7
Anpassung der theoretischen Verteilung<br />
(Endres 2005)<br />
Problem: Langreichweitige Korrelationen<br />
Normierte Wiederkehr<strong>in</strong>tervalle der Schwellwertüberschreitungen<br />
(Endres 2005)<br />
8
Übersicht<br />
1. Def<strong>in</strong>ition und Eigenschaften von Zeitreihen<br />
2. Tests und Trenderkennung für Zeitreihen<br />
3. Fourriertransformation, Powerspektrum<br />
4. Wavelets<br />
5. Zeitreihenmodellierung der ARMA-Klasse (kurzes Gedächtnis)<br />
6. Modellierung von Zeitreihen mit langem Gedächtnis<br />
7. Komplexität und Information von Zeitreihen<br />
8. Wiederkehranalyse<br />
9. S<strong>in</strong>guläre System-Analyse<br />
10. Bruchpunktanalyse<br />
11. Extremwertanalyse<br />
Zeitreihen<br />
• E<strong>in</strong>e Zeitreihe ist e<strong>in</strong>e Menge von Werten, die <strong>in</strong> e<strong>in</strong>er<br />
festgelegten (und bekannten!) Reihenfolge vorliegen.<br />
• Zeitreihen rechtfertigen eigene statistische Verfahren (und<br />
e<strong>in</strong>e eigene Vorlesung), weil sie <strong>in</strong> der Regel autokorreliert<br />
s<strong>in</strong>d.<br />
Gegenbeispiel: Weißes Rauschen<br />
9
Korrelation etc.<br />
Varianz<br />
Maß für<br />
Streuung um den Mittelwert<br />
Mathematisch<br />
mittlere quadrierte Abweichung<br />
Kovarianz<br />
Korrelation<br />
<strong>Regression</strong><br />
Faltung<br />
Enge des l<strong>in</strong>earen Zusammenhangs<br />
zwischen zwei Variablen<br />
Enge des l<strong>in</strong>earen Zusammenhangs<br />
zwischen zwei Variablen<br />
Art des Zusammenhangs zwischen<br />
mehreren Größen<br />
Enge des Zusammenhangs zweier<br />
Zeitreihen bzw. Funktionen<br />
mittlere quadrierte Abweichung zweier<br />
Variablen jeweils von ihrem Mittelwert<br />
auf [-1;1]-normierte Kovarianz<br />
(Teilung durch das Produkt der<br />
Standardabweichungen)<br />
Funktion<br />
gemitteltes Produkt zweier gegene<strong>in</strong>ander<br />
verschobener Zeitreihen bzw. Funktionen<br />
Übersicht<br />
Verfahren<br />
Ziel<br />
global/lokal<br />
Instationaritäten<br />
Periodizitäten<br />
(saisonaler) Kendall-Test<br />
Analyse<br />
global<br />
des Mittelwerts<br />
-<br />
Bartlett-, Levene-Test<br />
Analyse<br />
global<br />
der Varianz<br />
-<br />
Stationaritätstest nach Witt<br />
Analyse<br />
lokal<br />
der Verteilung<br />
-<br />
Fourierspektrum, Periodogramm<br />
Analyse<br />
global<br />
-<br />
Frequenz-scharf<br />
(harmonische)<br />
Power-Spektrum<br />
Analyse<br />
global<br />
-<br />
Frequenz-scharf<br />
(allgeme<strong>in</strong>)<br />
Wavelet-Analyse<br />
Analyse<br />
lokal<br />
des Frequenzspektrums<br />
Frequenz-scharf<br />
(harmonische)<br />
ARIMA-Modelle<br />
Modellierung<br />
global<br />
-<br />
-<br />
Hurst-Koeffizient<br />
Analyse<br />
global<br />
(langreichweitige Korrelationen)<br />
-<br />
Komplexität und Information<br />
Analyse<br />
global<br />
-<br />
-<br />
Wiederkehranalyse<br />
Analyse<br />
lokal<br />
der Dynamik (Attraktoren)<br />
annähernd<br />
S<strong>in</strong>guläre System-Analyse<br />
Analyse<br />
lokal<br />
der Dynamik (Attraktoren)<br />
annähernd<br />
Doppelsummenkurve<br />
Analyse<br />
lokal<br />
des Verhältnisses zweier Variablen<br />
-<br />
Bruchpunktanalyse (i.e.S.)<br />
Analyse<br />
Lokal<br />
des Mittelwertes<br />
-<br />
Progressive Detrended Fluctuation<br />
Analysis<br />
Analyse<br />
lokal<br />
der Varianz, der Korrelationen<br />
-<br />
Extremwertanalyse<br />
Analyse<br />
global<br />
-<br />
-<br />
10