11 Vektoranalysis

11 Vektoranalysis 54
11 Vektoranalysis
Wir wollen nun Vektorfelder betrachten.
Definition Es sei U ⊂ R n . Ein Vektorfeld im R n ist eine Abbildung v : U →
R n , die jedem Punkt x ihres Definitionsbereichs U einen Vektor v(x) zuordnet.
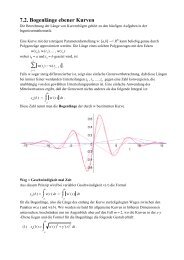
Abbildung 14: Ein Vektorfeld im R 2
Wir können ein Vektorfeld v graphisch darstellen, indem wir in jedem Punkt
den zugeordneten Vektor zeichnen (vgl. Abbildung 14). Dabei ist es zweckmäßig,
den Vektor v(x) in x beginnen zu lassen anstatt im Ursprung. Wenn die Abbildung
v zur Klasse C k gehört, sagen wir auch, das Vektorfeld v gehört zur
Klasse C k . Wir setzen im Folgenden voraus, dass Vektorfelder mindestens zur
Klasse C 1 gehören. Wir werden im Folgenden auch ausschließlich Vektorfelder
im R 2 oder R 3 betrachten. Für ein solches Vektorfeld benutzen wir die Notation
⃗v anstelle von v.
Beispiel 11.1 Wir betrachten eine Flüssigkeit, die sich durch ein Rohr bewegt.
Ordnen wir jedem Punkt der Flüssigkeit den zugehörigen Geschwindigkeitsvektor
zu, dann erhalten wir das vektorielle Geschwindigkeitsfeld ⃗v der Flüssigkeit.
Beispiel 11.2 Die Anziehungskraft einer Masse M, die sich im Ursprung des
R 3 befindet, auf eine Masse m lässt sich durch ein Vektorfeld ⃗v im R 3 , das
Gravitationsfeld, beschreiben. Nach dem Newton’schen Gravitationsgesetz gilt:
⎛
− mMG ⎞
r
x
⃗v = ⎝
3
y ⎠ ,
− mMG
r 3
− mMG
r 3
wobei G die Gravitationskonstante und r = √ x 2 + y 2 + z 2 ist. Es gilt
⃗v = − grad V mit V = − mMG ,
r
z

11 Vektoranalysis 55
wobei V das Gravitationspotential ist. Also ist ⃗v ein Gradientenfeld, d.h. Gradient
einer reellwertigen Funktion. Die Frage, wann ein Vektorfeld ein Gradientenfeld
ist, wird uns im Folgenden noch beschäftigen.
Definition
Ist ⃗v ein Vektorfeld, dann nennt man einen Weg σ(t), für den gilt
σ ′ (t) = ⃗v(σ(t)),
eine Bahnkurve oder Flußlinie von ⃗v. Geometrisch bedeutet dies, dass die Vektoren
von ⃗v in den Punkten von σ(t) die Geschwindigkeitsvektoren von σ(t)
sind.
In Beispiel 11.1 ist eine Bahnkurve genau der Weg, den ein kleines Teilchen,
das in der Flüssigkeit schwebt, beschreibt.
Wie findet man eine Bahnkurve durch einen Punkt a zu einem gegebenen
Vektorfeld ⃗v? Geometrisch sucht man eine Kurve, die durch den Punkt a geht
und deren Tangentialvektoren in allen Punkten mit den Vektoren des Vektorfeldes
⃗v identisch sind. Eine Bahnkurve, die zum Zeitpunkt t = 0 durch den Punkt
a läuft, findet man durch Lösen der Differentialgleichung
mit der Anfangsbedingung
σ ′ (t) = ⃗v(σ(t))
σ(0) = a.
Ist ⃗v ein Vektorfeld im R 3 , so entspricht dieser Differentialgleichung das System
von gewöhnlichen Differentialgleichungen
mit den Anfangsbedingungen
Es sei nun
x ′ (t) = v 1 (x(t), y(t), z(t))
y ′ (t) = v 2 (x(t), y(t), z(t))
z ′ (t) = v 3 (x(t), y(t), z(t))
(x(0), y(0), z(0)) = (a 1 , a 2 , a 3 ).
⃗v =
⎛
⎝ v 1
v 2
v 3
ein Vektorfeld im R 3 . Wir betrachten nun bestimmte Operationen auf Vektorfeldern.
⎞
⎠
Definition
Die Rotation von ⃗v ist das Vektorfeld
⎛
⎞
rot ⃗v =
⎜
⎝
∂v 3
∂y
− ∂v2
∂z
∂v 1
∂z − ∂v 3
∂x
∂v 2
∂x − ∂v 1
∂y
⎟
⎠ .

11 Vektoranalysis 56
Um eine Merkregel für die Rotation eines Vektorfeldes zu notieren, führen
wir das Symbol ∇ ein:
( ∂
∇ =
∂x , ∂ ∂y , ∂ )
.
∂z
Das Symbol ∇ ist ein Operator für reellwertige Funktionen. Ist f : R 3 → R eine
reellwertige Funktion, so gilt
( ∂f
∇f =
∂x , ∂f
∂y , ∂f )
.
∂z
Also ist ∇f der Gradient von f und unsere Notation stimmt mit der alten
Notation überein. Fassen wir ∇ als einen Vektor im R 3 auf und bezeichnen wir
die Vektoren der Standardbasis des R 3 mit
⎛ ⎞ ⎛ ⎞ ⎛ ⎞
⃗e 1 =
⎝ 1 0
0
⎠ , ⃗e 2 =
⎝ 0 1
0
⎠ , ⃗e 3 =
⎝ 0 0
1
so können wir das Vektorprodukt ∇ × ⃗v bilden und es gilt
∣ ⃗e 1 ⃗e 2 ⃗e 3 ∣∣∣∣∣
rot ⃗v = ∇ × ⃗v =
∂ ∂ ∂
∂x ∂y ∂z
.
∣ v 1 v 2 v 3
⎠ ,
Beispiel 11.3 Für
gilt:
⎛
⃗v = ⎝
x xy
1
⎞
⎠
⃗e 1 ⃗e 2 ⃗e 3
rot ⃗v = ∇ × ⃗v =
∂ ∂
∂x ∂y
∣ x xy 1
∂
∂z
⎛
∣ = ⎝ 0 0
y
⎞
⎠ .
Satz 11.1 Für jede C 2 -Funktion f : R 3 → R gilt:
rot(∇f) = ∇ × (∇f) = ⃗0,
d.h. die Rotation eines Gradienten ist der Nullvektor.
Beweis. Es gilt
∇ × (∇f) =
∣
⃗e 1 ⃗e 2 ⃗e 3
∂
∂x
∂f
∂x
∂
∂y
∂f
∂y
∂
∂z
∂f
∂z
⎛
∣ = ⎜
⎝
∂ 2 f
∂y∂z − ∂2 f
∂z∂y
∂ 2 f
∂z∂x − ∂2 f
∂x∂z
∂ 2 f
∂x∂y − ∂2 f
∂y∂x
⎞
⎟
⎠ .
Da f zur Klasse C 2 gehört, sind nach Satz 6.1 die gemischten partiellen Ableitungen
zweiter Ordnung gleich und damit ist jede Komponente gleich Null.
✷

11 Vektoranalysis 57
Beispiel 11.4 Es sei
Dann gilt
⎛
⃗v = ⎝
y
−x
0
⃗e 1 ⃗e 2 ⃗e 3
rot ⃗v =
∂ ∂
∂x ∂y
∣ y −x 0
∂
∂z
Also ist nach Satz 11.1 ⃗v kein Gradientenfeld.
⎞
⎠ .
⎛
∣ = ⎝ 0 0
−2
⎞
⎠ ≠ ⃗0.
Ein anderer Grundoperator ist die Divergenz, die nun definiert werden soll.
Definition
Die Divergenz eines Vektorfelds ⃗v ist das skalare (!) Feld
Beispiel 11.5 Für
gilt:
div ⃗v = ∇ · ⃗v = ∂v 1
∂x + ∂v 2
∂y + ∂v 3
∂z .
⎛
⃗v = ⎝
x xy
1
div ⃗v = ∂
∂x (x) + ∂ ∂y (xy) + ∂ (1) = 1 + x.
∂z
Satz 11.2 Für jedes C 2 -Vektorfeld ⃗v gilt:
⎞
⎠
div rot ⃗v = ∇ · (∇ × ⃗v) = 0,
d.h. die Divergenz einer Rotation ist gleich Null.
Beweis. Es gilt:
div rot ⃗v =
( ∂
∂x , ∂ ∂y , ∂ ∂z
) ⎛ ⎜ ⎝
∂v 3
∂y
− ∂v2
∂z
∂v 1
∂z − ∂v 3
∂x
∂v 2
∂x − ∂v 1
∂y
⎞
⎟
⎠
= ∂2 v 3
∂x∂y − ∂2 v 2
∂x∂z + ∂2 v 1
∂y∂z − ∂2 v 3
∂y∂x + ∂2 v 2
∂z∂x − ∂2 v 1
∂z∂y = 0.
✷
Beispiel 11.6 Für
gilt:
⎛ ⎞
⃗v = ⎝ x2 y
z ⎠
xyz
div ⃗v = ∂
∂x (x2 y) + ∂ ∂y (z) + ∂ (xyz) = 2xy + xy = 3xy.
∂z
Aus Satz 11.2 folgt, dass ⃗v nicht Rotation eines anderen Vektorfelds sein kann.

11 Vektoranalysis 58
Definition
Der Laplace-Operator ∇ 2 für Funktionen f ist wie folgt definiert:
∇ 2 f = ∇ · (∇f) = ∂2 f
∂x 2 + ∂2 f
∂y 2 + ∂2 f
∂z 2 .
Bemerkung 11.1 Man schreibt für den Laplace-Operator auch oft
∆ := ∇ 2 .
Damit stehen uns nun drei sogenannte Differentialoperatoren zur Verfügung.
Es gelten verschiedene Rechenregeln für diese Operatoren. Satz 11.1 und
Satz 11.2 sind Beispiele dafür. Eine weitere Rechenregel, die im wesentlichen
eine Variante der Produktregel ist, notieren wir in dem folgenden Satz.
Satz 11.3 Es gilt
div(f⃗v) = f div ⃗v + ⃗v · ∇f.
Beweis. Es gilt
div(f⃗v) = ∂
∂x (fv 1) + ∂ ∂y (fv 2) + ∂ ∂z (fv 3)
= f ∂v 1
∂x + v ∂f
1
∂x + f ∂v 2
∂y + v ∂f
2
∂y + f ∂v 3
∂z + v ∂f
3
∂z
( ∂v1
= f
∂x + ∂v 2
∂y + ∂v )
3 ∂f
+ v 1
∂z ∂x + v ∂f
2
∂y + v ∂f
3
∂z
= f(∇ · ⃗v) + ⃗v · ∇f.
✷