Adaptive Finite-Elemente-Methoden zur L osung der ...

FakultatfurPhysikundAstronomie Ruprecht-Karls-UniversitatHeidelberg 

AdaptiveFinite-Elemente-Methodenzur 

AnwendunginderPhysikderSonne LosungderWellengleichungmit 

imStudiengangPhysik Diplomarbeit 

ausRuitaufdenFildern WolfgangBangerth vorgelegtvon 

1998

AdaptiveFinite-Elemente-Methodenzur 

AnwendunginderPhysikderSonne LosungderWellengleichungmit 

InstitutfurAngewandteMathematikderUniversitatHeidelberg DieDiplomarbeitwurdevonWolfgangBangerthausgefuhrtam 

HerrnProfessorRolfRannacher unterderBetreuungvon 

HerrnProfessorPeterUlmschneider InstitutfurTheoretischeAstrophysik sowievon

Allen,diemichhierherbegleitethaben.

Zusammenfassung: ImRahmendieserArbeitwerdenadaptiveMethodenzurnumerischenLosungderWellengleichungininhomogenenMedienhergeleitetundaufeinBeispielausderPhysik 

LosungbezuglicheinesbeliebigenFunktionals(dieAuswertungsgroe)abzuschatzenund dieSchatzungzurErzeugungvonGitternzuverwenden,dieoptimalandasFunktional angepatsind. VorteileundSchwierigkeitenderMethodewerdenprasentiert.Insbesonderewirdgezeigt,dadervorgeschlageneAnsatzinvielenFallenezienteralsbisherigeadaptive 

derSonnenatmosphareangewandt.ZielderArbeitistes,denFehlerdernumerischen 

mosphareangewandtunddieAusbreitunglinearerakustischerWellenberechnet.Der DievorgeschlageneMethodewirdaufeineinfachesModellderPhysikderSonnenat- 

Methoden,diedasZielfunktionalnichtmitberucksichtigten,ist.IndenFallenmitnichtlinearenZielfunktionalen,indenendasVerfahrennichtfunktionierte,werdentheoretische 

ErklarungenundnumerischeErgebnissedesFehlschlagensgegeben. Koronapassierenkann,wirdmitguterGenauigkeitbestimmt. AnteilderEnergiederWellen,derdenUbergangzwischenderChromosphareundder 

Abstract: 

Inthiswork,adaptiveconceptsforthenumericalsolutionofthewaveequationininhomogeneousmediaarederivedandappliedtoanexampletakenfromthephysicsof 

AdaptiveFiniteElementMethodsfortheSolutionoftheWaveEquationand 

thesolaratmosphere.Themainfocusisonwaystoestimatetheerrorinthenumerical ApplicationtoSolarPhysics 

ofthisfunctional. Advantagesanddicultiesofthismethodarepresented.Inparticular,itisshownthat solutionwithregardtoarbitraryfunctionals,i.e.quantitiesofinterest,andtheuseof theseestimatesforthegenerationofcomputationalmeshesbestsuitedfortheevaluation theproposedapproachissignicantlybetterinmanycasesthanpreviousadaptiveschemesnottakingintoaccountthequantityofinterest.Casesinvolvingnonlinearfunctionals 

atmosphereandthepropagationoflinearacousticwavesiscomputed.Thefractionof Theproposedmethodsareappliedtoasimplemodelfromthephysicsofthesolar numericalevidenceofthereasonsforthis. andinwhichtheapproachfails,arepresentedalongwiththeoreticalexplanationsand thewaveenergythatpassesthechromosphere{coronatransitioniscomputedtogood accuracy.

Inhaltsverzeichnis 

1Einfuhrung 2NumerikderWellengleichung 2.1Zeitdiskretisierung.................................... 31 

2.1.1Das-Verfahren................................. 2.1.2DasFractional-Step--Verfahren........................ 45 

2.3VolldiskretisierungineinemSchritt...........................11 2.2Ortsdiskretisierung....................................10 2.1.3VergleichderZeitschrittverfahren........................ 6 

2.3.1HangendeKnotenimOrt............................13 7 

2.4Fehlerkontrolle......................................15 2.4.1VorbemerkungenundNotationen........................15 2.3.3EntkopplungderGleichungen..........................15 2.3.2HangendeKnoteninderZeit..........................14 

2.4.2ExakteFehlerdarstellung............................16 2.4.3AuswertungmithoheremAnsatzgrad.....................18 2.4.5VergleichderbeidenWegederAuswertung..................25 2.4.4AbschatzungmitdemBramble-Hilbert-Lemma................20 

3AnwendungaufdiesolareAtmosphare 2.4.6BewertungderLinearisierungnichtlinearerZielfunktionale..........26 

3.1DenitiondesGebietsundderRandbedingungen...................33 2.4.7BewertungdernumerischendualenLosung..................28 

3.2AuswertungderRechnungen..............................35 3.3Adaptivitat........................................37 31 

3.4ErgebnissederRechnungen...............................38 3.4.2VerfeinerungmitdemdualenSchatzer.....................41 3.4.3GlobaleVerfeinerung...............................45 3.4.1VerfeinerungmiteinemEnergiefehlerindikator................39 

4TechnischeAspektederImplementation 4.2TransfervoneinemGitterzumanderen........................48 4.3BehandlungvonDirichlet-Randwerten.........................49 4.1Diedeal.II-Bibliothek..................................47 47 

4.4BehandlungvonhangendenKnotenimOrt......................51 4.5SteuerungdesGitters..................................52 4.5.2h-AbhangigkeitderDispersionsrelation.....................55 4.5.1AuseinanderdriftenderGitter..........................52 4.5.3Orts-Zeit-Adaptivitat..............................57 vii

viii 5WeiterenumerischeBeispiele INHALTSVERZEICHNIS 

5.2WinkelabhangigkeitderAusbreitungsgeschwindigkeit.................64 5.1ZeitintegraleinerPunktauswertung...........................60 5.3StreuunganvielenDiskontinuitaten..........................66 5.4TeilweiseReexionanGitterunstetigkeiten......................68 59 

AAprioriFehlerschrankenfurZeitschrittverfahren A.1Vorbemerkungen.....................................73 A.2DasimpliziteEuler-Verfahren..............................75 A.2.1Verfahren.....................................75 A.2.2Analyse......................................75 

A.3Das-Verfahren......................................78 A.4DasDG(1)-Verfahren...................................81 A.3.1Verfahren.....................................78 A.3.2Analyse......................................79 A.4.1Verfahren.....................................81 

ZusammenfassungundAusblick A.6VergleichderVerfahren.................................84 A.5BedeutungderBedingung"~u(p)=0furjpjp0\...................83 A.4.2Analyse......................................82 

Notationen Literaturverzeichnis 87 91 89

Kapitel1 

Einfuhrung 

ImRahmendieserArbeitsolldienumerischeLosungderWellengleichung (x)utt(x;t)?r(a(x)ru(x;t))=0 u(x;0)=u0(x) (x;t)2(0;T); 

na(x)ru(x;t)=gN(x;t) ut(x;0)=v0(x) u(x;t)=gD(x;t) x2; x2?D(0;T);?D@; x2?N(0;T);?N=@??D; (1.1) 

undihreAnwendungaufdenEnergietransportinderunterensolarenAtmosphareuntersucht werden.DiesersolldabeidurchakustischeWellensimuliertwerden,diesichinFormderobigenGleichungenalsGrenzfallkleinerStorungenausdenEuler-GleichungenderGasdynamik 

ergeben;indiesemFallistudieAbweichungdesDrucksvomGleichgewichtswert,dieDichte diewesentlichen,nichtlinearenEektederSchallausbreitungindunnen,ionisiertenGasenauer achtlat.EsistabereinersterSchrittinRichtungzumehrdimensionalenRechnungen,diees undadieinverseKompressibilitatdesMediums.DieseNaherungistnichtbesondersgut,dasie erlauben,MechanismenderAusbreitunginMedienmitvariablenAusbreitungskoezientenzu untersuchen,insbesondereReexionanGrenzschichtenundRefraktion;dieseEektesindinden Einuabzuschatzen. Wellengleichungeinsetzbarsindundobesmoglichist,a-posterioriFehlerschatztechnikenanzuwenden.AufgrundderbereitsinzweiRaum-undeinerZeitdimensionsehrhohenAnforderungen 

anRechenzeitundSpeicherbedarferscheintesunabdingbar,adaptiveTechnikenzuverwenden, dieimGegensatzzugleichformigenoderblockweisegleichformigenGitterndieRechenzellendort VondernumerischenSeitehersolluntersuchtwerden,obadaptiveTechnikenimKontextder bisherdurchgefuhrteneindimensionalenRechnungennichtdarstellbar,sodaeswichtigist,ihren 

plazieren,woderFehlererzeugtwird.DieBerucksichtigungderHerkunftdesFehlersunterscheidet denvorgestelltenAnsatzdamitinsbesonderevonbisherigenAnsatzenzurGittersteuerung,dienur dortverfeinerten,woderFehlergroist.DieNotwendigkeitadaptiverTechnikengiltumsomehr beiRechnungenmitdreiRaumdimensionenoderwenneinehoheGenauigkeitgefordertist,dadie GitterverfeinerunginderLageist,diebenotigtenRessourcenerheblichzusenkenundaufgrund deutlichgeringerenSpeicherbedarfseinigeRechnungenerstmoglichzumachen. herkommlichenTechnikendiesesnichtmehrzuleistenvermogen.Eswirdgezeigt,daadaptive 

interessiert,sondernanderAuswertungeinesFunktionalsderLosung,zumBeispieleinemPunktwert,LinienintegralenodergewichtetenIntegralen.Esistklar,daeinoptimalesRechengitter 

BezuglichderGitterverfeinerungsollinsbesondereeinAnsatzuntersuchtwerden,dereine istmanseltenamFehlerineinerabstraktenNorm,beispielsweisederL2-oderderEnergienorm, SchatzungdesFehlerbeiderAuswertungeinesbeliebigenFunktionalsverwendet.InderPraxis aufdieseAuswertegroeabgestimmtseinmu,wobeidasZielist,beigleichzeitigerMinimierung derAnzahlanFreiheitsgradendenFehlerbeiderAuswertungdesFunktionalszuminimieren. Dieskannbedeuten,voneinerdurchdasGebietlaufendenWellenurdenTeilgutaufzulosen,der 1

2schlielichauchzumzuberechnendenFunktionalwertbeitragt,wahrenddieTeilederWelle,die 

inandereRichtungenlaufen,nichtaufgelostwerdenmussen.EswirdeinAnsatzvorgestellt,der KAPITEL1.EINFUHRUNG 

dieGitterverfeinerungautomatisch,d.h.ohneInteraktiondesBenutzers,nachdiesemKriterium durcheinDierenzen-oderCharakteristikenverfahrenmitexpliziterZeitdiskretisierung,sondern durchfuhrt. mittelsFinitenElementenundimplizitenZeitschrittverfahren.FiniteElementeerlaubengegen- unabdingbarfurdieVerwendungadaptiverVerfahrenist;daruberhinauslassensicha-posteriori- uberDierenzenverfahrenwesentlichgroereFreiheitenbeiderGestaltungderRechengitter,was ImGegensatzzudenmeistenRechnungenderVergangenheiterfolgtdieDiskretisierungnicht 

sodaeinegezielteVerfeinerungeinzelnerZellenmoglichist.GegenuberCharakteristikenverfahrenzeichnetsieaus,dadieHerangehensweiseimwesentlichendimensionsunabhangigist;ihre 

UmsetzungbietetfurzweiodermehrRaumdimensionenkeinewesentlichenzusatzlichenmathe- 

sindallerdingsnursehrschweraufhohereRaumdimensionenverallgemeinerbarundAbschatzungendesFehlerssindschwierig(vgl.[26]).DieverwendetenFinitenElementesindbilinearebis 

Fehlerschatzerherleiten,dieInformationenuberdenBeitrageinerZellezumGesamtfehlerliefern, 

gegendiekontinuierlicheLosungderverwendetenGleichungnahezuexaktimDiskretenwieder, matischenSchwierigkeitengegenubereinerRaumdimension.Charakteristikenverfahrengebenda- 

kann,wurdedieseinesehrkleineZeitschrittweitenachsichziehen,wasdenRechenaufwandenorm kleinstenZellenbindet;dadieZellgroevariabelistundbeiadaptivenVerfahrensehrkleinwerden EinhaltungeinerBedingung("CFL-Bedingung\)verlangt,diedieZeitschrittweiteandieGroeder biquartischekonformeElementeaufVierecksgittern. 

erhohenwurde.ImRahmendieserArbeitwurdenzurZeitdiskretisierungdasCrank-NicolsonsowiedasFractional-Step--Verfahrenverwendet. 

ImpliziteZeitschrittverfahrenwerdeneingesetzt,dadieVerwendendungexpliziterVerfahrendie 

einfachenWegbegleitet,gefuhrtundmirzurSeitegestandenhaben,zugroemDankverpichtet! Ichbinallen,meinenEltern,Freunden,BetreuernundKollegen,diemichaufdiesemoftnicht AnderEntstehungeinerArbeitwiediesersindmehrMenschenalsnurderAuthorbeteilgt.

Kapitel2 

NumerikderWellengleichung 

ZurBehandlungderWellengleichungaufdemComputeristesnotig,dieinkontinuierlichenKoordinatengeschriebenenGleichungenzudiskretisieren.ImRahmendieserArbeitsolldabeifolgende 

Diskretisierunguntersuchtwerden: zeitlich:DiezeitlicheAbleitungwirddadurchdiskretisiert,dawirdieGleichung(1.1)in 

raumlich:AnschlieendwirddieraumlicheAbleitungmiteinemFinite-Elemente-Verfahren Verfahren)diskretisieren. einSystemvonpartiellenDierentialgleichungenersterOrdnunginderZeituberfuhrenund 

mitstuckweisepolynomialenAnsatzfunktionenbehandelt.AlsPolynomewerdendieLagrange-InterpolationspolynomederOrdnungeneinsbisvierbetrachtet. 

diesemiteinemdergangigenVerfahren(-bzw.Crank-Nicolson-undFractional-Step-unddasdadurchentstehendeSystemgekoppelterDierentialgleichungeninderZeitmiteinegensatzzursogenanntenLinienmethode,beiderzuerstdieOrtsdiskretisierungdurchgefuhrtwird 

DieseReihenfolgederDiskretisierungwirdgemeinhinalsRothe-Methodebezeichnet,imGenenvergleichbareErgebnisse.LediglichdieAnalysedesFehlersunterscheidetsichwesentlich.Die 

Rothe-MethodehataberentscheidendeVorteilebeiderVerwendungortsadaptiverGitter,dain derbekanntenVerfahrenzurLosunggewohnlicherDierentialgleichungssystemebehandeltwird. 

diesenFallenAnzahlundOrtderFreiheitsgradevonZeitschrittzuZeitschrittvariieren,weshalb sichdiepartielleDierentialgleichungnichtmehrohneweiteresineinSystemvongewohnlichen FurgleichbleibendeGittersindbeideMethodenimwesentlichengleichundliefernimallgemei- 

Dierentialgleichungenumschreibenlat. transportiertwerdenmu,bleibtjedochbestehen.HiererweistsichdieVerwendunghierarchisch aufgebauterGitteralsausgesprochenvorteilhaft,daesnichtnotigist,herauszunden,inwelcher ZelledesGitterseinPunktliegt,wieesnotigware,wenndieGitterzuverschiedenenZeitschritten vollstandigunabhangigwaren.Programme,diemitvolligunabhangigenGitternarbeiten,verbringenofteinenGroteilderZeitmitsolchenAufgaben(vgl.[29,Remark2.2]).DerTransferzwischegerGitterauf. 

inderZeitunddannimOrtdiskretisiert,sondernineinemSchritt.SoferndieZeitdiskretisierung miteinemGalerkin-Verfahrenerfolgt,sinddiebeidenHerangehensweisenidentisch.Dasichdie AufteilunginZeit-undOrtsdiskretisierungfurdieImplementationaufeinemComputerbesser eignet,wirdzuersteinehalbformaleHerleitungderDiskretisierunginzweiSchrittenunddaran UmeinenstrengmathematischenRahmenzuschaen,wirddieGleichungnichtwieobenerst 

DasProblem,dadieLosungzueinemZeitschrittaufdasGitterdesnachstenZeitschritts 

werden(Abschnitt4.2),d.h.estrittkeinInterpolationsfehlerwiebeiderVerwendungunabhangi- 

GitternkanndaruberhinausbeimAufbauderrechtenSeitederGleichungenexaktdurchgefuhrt 

anschlieendeinerigoroseAbleitungderVolldiskretisierunggegeben. IndenfolgendenAbschnittenwerdendiefolgendenNotationenverwendet: 3

4In=(tn?1;tn]seidasnteZeitintervallderZeitdiskretisierungundkn=tn?tn?1seine 

Lange; KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

I=(0;T]seidasgesamteinteressierendeZeitintervall;oenbaristI=SnIn; DieLosungsfunktionseiw=(u;v).DieLosungdesinAbschnitt2.4.2eingefuhrtendualen t=('; (p;q)bezeichnetdasL2-SkalarproduktRpqdx;fallspundqVektorensind,seidasVektorproduktimpliziert; 

)kennzeichnetimallgemeineneineTestfunktion; Problemsseiw=(u;v);derUberstrichkennzeichnedualenGroen; 

b(w;t)seidiedurchb(w;t)=0 nierteBilinearform. a(x)r0w;10 ? 0rt[0;T]?(gN; )?N[0;T]de- 

2.1 DieUmschreibungineinSystemersterOrdnunginderZeitgeschiehtfolgendermaen:wirgehen von Zeitdiskretisierung 

aus(a(x;t)istentwedereinestriktpositiveskalareFunktionodereinepositivdenite,symmetrischedd-Matrix,isteinestriktpositiveFunktion)undsetzenv=ut.DerEinfachheithalber 

seiangenommen,dadieKoezientenaundnichtvonderZeitabhangen.DiesistimEinklang (x)utt(x;t)?r(a(x;t)ru(x;t))=0 (2.1) 

mitderFragestellungdieserArbeit;dieErweiterungbezuglichderMethodikbeizeitlichvariablen KoezientenistindenmeistenFallenoensichtlich.SeiauerdemA=?r(ar)derpositiv deniteraumlicheOperator,danngilt 

DieseGleichunglatsichmitw=(u;v)unddemOperatorB=0? ut vt+0? A0uv=0: A0verkurztauchals (2.2) 

DierentialgleichungimHilbertraumschreiben: DieersteGleichungwurdemitmultipliziert,dadannalleMassematrizendiesenFaktorenthalten. DaruberhinauslatsichsodienumerischeStabilitaterhohen,dadieeinzelnenTermevonder gleichenGroenordnungsind;dasistinsbesonderebeideminAbschnitt3gerechnetenBeispiel wt+Bw=0: (2.3) 

wichtig,wodieKoezientenumbiszudreiZehnerpotenzenvariieren. zweiVorteile: DieUmschreibungineinSystemhatgegenuberderdirektenLosungvon(2.1)imwesentlichen ZurDiskretisierungersterZeitableitungenexistierteineVielzahlvongutuntersuchtenVerfahrenausderNumerikdergewohnlichenDierentialgleichungen.DortwerdenhohereAblei- 

GegenuberderdirektenDiskretisierung(beispielsweisedurcheinenAnsatzahnlichderDiskretisierungdesLaplace-Operators)kannmaneinebessereKonvergenzordnungfurdigenumgeformt,sodazurdirektenDiskretisierungzweiterAbleitungennurrelativwenigtungenimallgemeinendurchEinfuhrungzusatzlicherVariablenineinSystemvonGleichun- 

Verfahrenbekanntsind. zweiteVariableverwarten,analogzurVerwendungeinergemischtenDiskretisierungim

2.1.ZEITDISKRETISIERUNG ten,beispielsweisedieEnergieE=(v;v)+(aru;ru); Ort.DashatVorteile,davielepraktischrelevanteFunktionaledieGeschwindigkeitenthal- 

5 

oderderEnergieudurcheineKurve 

BeidirekterDiskretisierungwirddieImplementationschnellsehrunubersichtlich,daDaten ubermehralseinenZeitschritttransportiertwerdenmussen. =ZCvarunds: 

DemstehtalsNachteilallerdingsgegenuber,dadiemitdemSystemassoziierteBilinearform keinenaturlicheNorminduziert,sodaaprioriAbschatzungenundStabilitatsanalysenerschwert sind.DiesesindjedochinderLiteraturzunden,vgl.beispielsweise[16]unddieReferenzendarin. diskretisiertwerden.DabeikennzeichnenindenfolgendenAbschnittenobereIndizes(Superskripte)dieLosungenzubestimmtenZeitpunkten,z.B.istWnW(tn),wobeiW(t)dieLosungdes 

semidiskretenProblemssei.UmdieNotationubersichtlichzuhalten,sinddieVerfahrenmeistnur furdenerstenZeitschritt,dasheitfurW1undW0angegeben;dieUmsetzungfurallgemeine DasGleichungssystem(2.3)sollimfolgendenmiteinemderbekanntenVerfahreninderZeit 

beziehen,istdiesexplizitangemerkt. wahlensein.DanurEinschrittverfahrenbeschriebenwerden,seiderEinfachheithalberaufden Wn+1undWnistoensichtlich.BeiGleichungen,diesichausschlielichaufdenerstenZeitschritt Indexverzichtet. WieublichbezeichnekdieZeitschrittweite.Imallgemeinenwirdk=kn,d.h.variabelzu 

2.1.1Das-Verfahren Das-Verfahrenauf(2.3)angewandtlatsichwiefolgtschreiben: W1?W0 k +BW1+(1?)BW0=0: undmangelangtzuzweiTeilschritten: DurchUmschreiben1latsichdiegleichzeitigeLosungzweiergekoppelterLosungenvermeiden (2.4) 

DurchdieWahlvonlassensichaus(2.4)verschiedenebekannteVerfahrengewinnen: (+k22A)u1=u0+kv0?k2(1?)Au0 v1=v0?kAu1?k(1?)Au0 (2.5) 

=0:BeidieserWahlist(2.4)dieDiskretisierungderkontinuierlichenGleichungdurchdas expliziteEuler-Verfahren.AlsexplizitesVerfahrenhatesdenVorteil,dakeineDierentialgleichungimOrtgelostwerdenmu,dasheitW1hangtexplizitvonW0abundkann 

durchMatrix-Vektor-Multiplikationengewonnenwerden.DerwesentlicheNachteildesVerfahrensliegtinderKopplungderZeitschrittweiteandieGroederkleinstenZellen,diedarin 

begrundetliegt,daaufgrunddesexplizitenCharaktersInformationproZeitschrittnuruber 

Formulierungzeigen,danurdanndieunterschiedlichenRaume,ausdenenuundvkommen,korrektbehandelt 1DieUmformungerscheintaufdenerstenBlickoensichtlich.IhreRichtigkeitlatsichabernurinderschwachen hochstenseineZelletransportiertwerdenkann;solldieAusbreitungsgeschwindigkeitrichtig 

werdenkonnen;vgl.Abschnitt2.3.3. 2ImFallgleichformigerGittergiltdaruberhinausdieCourant-Friedrichs-Lewy-Bedingung(vgl.[13]),dieden wiedergegebenwerden,sodarfdieZeitschrittweitenichtzugrogewahltwerden.2 

VerlustderStabilitatdesVerfahrensbeschreibt,fallsfurZeitschrittkundGitterweitehdieBeziehungckCh verletztist,wobeicdieAusbreitungsgeschwindigkeitsei.DieKonstanteCistvonderOrtsdiskretisierungabhangig

6 schliet,dadiekleinstenZellensehrkleinwerdenkonnen,wennstarklokalisierteEigen- 

schaftenderLosunggutaufgelostwerdensollen. LetzteresisteineBedingung,diedenEinsatzimUmfeldadaptivverfeinerterGitteraus- 

KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

=1:IndiesemFallentstehtdasimpliziteEuler-Verfahren.EsiststarkA-stabilund DasexpliziteEuler-VerfahrenistvonersterOrdnung. ebenfallsvonersterOrdnung.FallsfurdenKoezientena(x;t)=a(x)gilt,unddawir diehomogeneWellengleichungbetrachten,istdiesesVerfahrenidentischmitdemunstetigen Galerkin-VerfahrennullterOrdnung,DG(0). 

=12:MitdieserWahlergibtsichdasCrank-Nicolson-Verfahren.EsistvonzweiterOrdnungundA-stabil,aberleidernichtstarkA-stabil,wassichimAuftretenvonOszillationen 

d.h.daesdieLosungglattetunddamitzueinemunphysikalischenVerlustanEnergieim DasimpliziteEuler-VerfahrenhatdenbedeutendenNachteil,daesstarkdissipativist, 

beiStorungenzeigenkann.TypischeStorungensindbeispielsweiseeinestarkeVeranderung Systemfuhrt;eskommtdamitnichtalsKandidatfureinesinnvolleImplementationinfrage. 

denGleichungenmussenbeiderStorungdurchGitteranderungOrtderStorungundOrt schwacherSignalestorenkann.AufgrundderElliptizitatderinjedemZeitschrittzulosenkumuliertsichimLaufederRechnungein"Untergrundrauschen\,dasbeiderAuswertungenschaftenderWellengleichungunddesZeitschrittverfahrensnichtgedampftwerden,ak- 

desGitters;dadiedadurchausgelostenOszillationenaufgrundderfehlendenGlattungsei- 

derOszillationennichtidentischmiteinandersein. VorteiledesCrank-Nicolson-VerfahrensindseinehohereOrdnungundvorallemdiefehlendeDissipativitat,diedieEnergieaufungestortenGitternexakterhalt.DasVerfahren 

zumindestteilweiseinAbhangigkeitvonderEnergieE0imletztenZeitschrittberechnen.Nach Aus(2.4)latsichaufdieEnergieE1=12?(aru1;ru1)+(v1;v1)zumneuenZeitschritt latsichalsPetrov-Galerkin-Verfahrenschreiben,wasinAbschnitt2.4zurHerleitung 

trivialerRechnungerhaltman vonFehlerschatzernverwendetwerdenwird. 

waserklart,weshalbdasCrank-Nicolson-VerfahrendieEnergieerhalt. E1=E0+k2(1?2)?rv0;aru1??rv1;aru0; 

FurdieGleichung(2.3)schreibtsichdasFractional-Step--Verfahren(imfolgendenmitFS-- 2.1.2DasFractional-Step--Verfahren Verfahrenabgekurzt)alsDreischrittverfahren: 

W1??W W?W0 k +BW+BW0=0; 

W1?W1? k +0BW1?+0BW=0; k +BW1+BW1?=0; (2.6) 

undliegtinderGroenordnungvon1. feinerteGitteristderZusammenhangzwischenGitterweitehunddenEigenwertenbekannt,nichtjedochfur UmstandentrotzdemeinstabilesVerfahrenergeben,dasbeschriebeneProblemmitdernumerischenAusbreitungsgeschwindigkeitbleibtjedochbestehen. 

lokalverfeinerteGitter.EinimVerhaltniszudenkleinstenZellenzugrogewahlterZeitschrittkanndaherunter DieCFL-BedingungwirduberdieGroederEigenwertederSystemmatrixhergeleitet.Furgleichformigver-

2.1.ZEITDISKRETISIERUNG 7 

mit=1?12p2,0=1?2,12

8 KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

70 

Crank-Nicolson 

60 

Euler implizit 

theta1=theta2=0.7 

theta1=0.5, theta2=1 

50 

Fractional step 

wahre Energie 

40 

30 

Abbildung2.1:VergleichderEnergiebeiverschiedenenZeitschrittverfahrenbeiregularverfeinertemGitterundglatterLosung(Beispiel1). 

20 

10 

0 

DaesindiesemerstenBeispielabernurdarumgeht,einigederVerfahrenauszusortieren,istdie 

0 0.5 1 1.5 2 

Wahlzurechtfertigen.DerVergleichderverbleibendenVerfahrenmiteinandererfolgtaneinem 

praxisrelevanterenBeispiel. Wellen.DieZeitschrittweitebetrugk=0:02(furdasFS--VerfahrenwurdederVergleichbarkeit halberk=0:06gewahlt),dasGebietwurdein192quadratischeZellenmith=1=8aufgeteilt. DieGrobheitdesGittersreichtsichernichtaus,umfeinereEinzelheitenderLosungaufzulosen, genugtaberumeinigederVerfahrenschonauszusortieren. DieLosungistbeliebigglattundzeigtkeineortlichveranderlichenEigenschaftenwielaufende 

AbnahmederEnergiebeimimplizitenEuler-VerfahrenaufgrunddessenDampfungseigenschaf- 

tenunddaauchdieanderenausdem-VerfahrenhergeleitetenMethodenauerdemCrank- Nicolson-VerfahrendieseEigenschaftbesitzen.DieWellenlinieentsprichteinemVerfahren,bei fahrenuberknappdreiPeriodenderEigenschwingungaufgetragen.Manerkenntdiezuerwartende InAbbildung2.1istderVerlaufderEnergieindernumerischenLosungfurverschiedeneVer- 

demdiebeidenGleichungen(2.4)mitunterschiedlichgewahltenParametern1und2diskretisiertwurden;diesesVerfahrendampftkinetischeundelastischeEnergieunterschiedlichstark, 

wodurchdieSchlangenliniezustandekommt.BeimCrank-Nicolson-VerfahrenbleibtdieEnergieaufmindestenssechsStellenkonstant,wenndasGitterkonstantbleibt.DieKonstanzder 

EnergieistunabhangigvomVerhaltnisvonOrts-zuZeitgitterweite,dasheitesexistiertkei- 

Phanomeneorientiertwerden.DieKurvedesFS--VerfahrensliegtpraktischaufderdesCrank- von610?5derEnergie.DaeinetypischeSimulationetwa200Zeitschrittebenotigt,istdieser Nicolson-Verfahrens,allerdingsverliertdasVerfahrenhierinjedemZeitschrittetwaeinenAnteil Fehlerbeitragimallgemeinentolerierbar. Beispiel2.IneinemzweitenBeispielwurdedasProblemmitfolgendenAnfangs-undRandwertengestellt: 

u(x;0)=8

2.1.ZEITDISKRETISIERUNG 9 

7 

6 

Durchlauf 3 

Durchlauf 4 

Durchlauf 5 

7 

6 

Durchlauf 3 

Durchlauf 4 

Durchlauf 5 

5 

5 

4 

4 

3 

3 

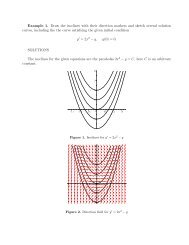
tional-Step--Verfahren(rechts)aufadaptivverfeinertenGittern.KoezientundLosungsind Abbildung2.2:VergleichderEnergiebeimCrank-Nicolson-Verfahren(links)undbeimFrac- 

2 

2 

nichtglatt(Beispiel2). 

1 

1 

0 

0 

0 0.2 0.4 0.6 0.8 1 1.2 1.4 

0 0.2 0.4 0.6 0.8 1 1.2 1.4 

InAbbildung2.2sindCrank-Nicolson-undFS--Verfahreneinandergegenubergestellt,wobeidieZeitschrittweitenaufk=0:02bzw.k=0:03gesetztwurde.DieRechnungwurdeauf 

adaptivverfeinertenGitternmitjeweilsinetwagleichenZellzahlenbeidenbeidenVerfahren eigenschaftenderZeitschrittverfahren.AlsFehlerindikatorwurdeeineinfacherEnergieschatzer nurderletzteDurchlaufwichtig;dievorhergehendengebenjedochAufschluuberdieStabilitats- 

nachKelly,Gago,ZienkiewiczundBabuskaderForm durchgefuhrt,wobeimehrereDurchlaufe4gemachtwurden.FurdenVergleichistimwesentlichen 

Zeit 

Zeit 

verwendet,vgl.[23].FurjedeZellewirddabeiderSprungderKonormalenableitung[na(x)ruh] zurNachbarzelleuberdenRandintegriert.EinekurzeBegrundungfurdiesenFehlerindikatorwird inAbschnitt2.4.4gegeben. VerfahrensamAnfangzueinemstarkerenEnergieverlustalsdasCrank-Nicolson-Verfahren GlattungvonUnstetigkeitenderLosungoderihresGradientenkonntenichtbestatigtwerden.Die letztlicheUrsacheistunbekannt. fuhrt.DieVermutung,dadiedissipativenEigenschaftendesVerfahrenseinesichtbarstarkere AusdenschonrechtglattenKurvendesletztenDurchlaufserkenntman,dadasFS-beidenZeitschrittweiten0.02bzw.0.03inetwadergleichenGroenordnungschrittssowiederFehlerschatzunggegenubergestelltwerdenmu,liegtdernumerischeAufwand 

AufwandaberderproZeitschrittnureinmalnotigenProjektionderLosungendesvorigenZeit- 

TrotzderTatsache,daproZeitschrittdreiGleichungssystemegelostwerdenmussen,dieser 

imglatterenVerlaufderKurveunddurchdieweitgehendfehlendenSprungeindenspateren Durchlaufenzeigt.DerEektistbesondersdeutlichinderjeweilsmittlerenderdreiKurvenzu sehen.DieseSprungewerdendurchdieStorunghervorgerufen,diedieVeranderungderGitter darstellt. InderAbbildungistandererseitsdiebessereStabilitatdesFS--Verfahrenszusehen,diesich 

Nicolson-VerfahrennichtalsGalerkin-Verfahrenschreibenlat.DamitfalltauchdienotwendigeGalerkin-OrthogonalitatwegunddieAbschatzungdesFehlersmittelseinesdualenProblems 

istnichtmehrmoglich.DadieserPunktdasVerfahrenfurdieZweckederFehlerschatzungimwe- 

ImPrinzipwaredasFractional-Step--VerfahreneinsehrguterKandidatfurdaszuverwendendeZeitschrittverfahren.EshatallerdingsdenNachteil,daessichimGegensatzzumCrankschrittenacheinanderaufdemGrobgittergerechnetwurde,imnachstenDurchlaufalleZeitschritteaufeinemeinmal 

verfeinertenGitter,usw.DetailsdazusindinAbschnitt4.5zunden. sentlichenausschliet,wirdimfolgendennurnochdasCrank-Nicolson-Verfahrenverwendet. BeideVerfahrenzeigenbeizunehmenderGitterverfeinerung,d.h.indenspaterenDurchlaufen, 4ZurBedeutungdesWortes"Durchlauf\:DieVerfeinerungerfolgteso,daineinemerstenDurchlaufalleZeit- 

Energie 

Energie 

2K=Chk[na(x)ruh]k2@K (2.9)

essereStabilitatseigenschaftenundKonvergenzgegeneinekonstanteEnergie,sodadieWahl desCrank-Nicolson-VerfahrenstrotzdergutenEigenschaftendesFS--Verfahrensvertretbar 10 KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

ist. 2.2 DurchdieuntersuchtenZeitschrittverfahrenentstandenjeweilszweiGleichungenderForm Ortsdiskretisierung 

wobei,,,,undvomVerfahrenundvonderZeitschrittweiteabhangigeKonstanten (+A)u1=u0+v0+Au0; v1=v0+Au1+Au0; (2.11) (2.10) 

wiederA=?ra(x)r.DieortlicheDiskretisierungdieserGleichungenwirdinderschwachen sind,derenWerthierauerdempositivenVorzeichenvon/k2keineRollespielt.Esgelte Problemnun: Formulierungdurchgefuhrt,diemandurchMultiplikationderGleichungenmiteinerTestfunktion undIntegrationuberdasGebieterhalt.BetrachtetmanGleichung(2.10),solautetdas Findeu12W,sodafuralle (u1;)+a(u1; 2Wgilt: 

DieFragederrichtigenFunktionenraumeistinKapitel2.3diskutiert.Essei(u;v)Ruvdx unda(u;v)RarurvdxderTerm,derdurchpartielleIntegrationvon(Au;v)entsteht.Wegen )=(u0;)+(v0;)+a(u0;): (2.12) 

dergefordertenEigenschaftenvona(x)und(x)sinda(;)und(;)symmetrische,positiv SeitenochumeinenRandintegraltermerganztwerden. deniteBilinearformen.SindinhomogeneNeumann-Randwertevorgeschrieben,mudierechte digerweiseumgekehrt,dadievariationelleFormulierung(2.12)geringereDierenzierbarkeitals (2.10)vonderLosungfordert(dafurwurdediepartielleIntegrationdurchgefuhrt).DieWellengleichunggarantiertnureineLosung,diegenausoglattistwieRand-undAnfangswertdaten,im 

allgemeinenalsou2L2mitzusatzlichenAnnahmenuberdieExistenzeinerSpuraufdemRand Losungenvon(2.10)sindselbstverstandlichauchLosungenvon(2.12),jedochnichtnotwen- 

undvonAnfangswerten;imRahmendieserArbeitseiaberindenmeistenFallenu(;t)2WH1 angenommen,wobeiH1derRaumderFunktionensei,deren(schwacher)Gradientnochquadratintegrabelist. 

dieTestfunktionenebenfallsauseinemendlichdimensionalenRaumThwahlen.DieDimensionNh derbeidenRaumemuubereinstimmen.DasvolldiskreteProblemlautetdamit: DieDiskretisierungimOrtwirdnunsodurchgefuhrt,dawirdieLosungnichtmehrim unendlichdimensionalenRaumWsuchen,sondernineinemendlichdimensionalenRaumWhund Findeu1h2Wh,sodafuralle (u1h; h)+a(u1h; h)=(u0h; h2Thgilt: 

untersucht;VerfahrenmitWh6=ThheienPetrov-Galerkin-Verfahrenundwerdenindieser FurdieOrtsdiskretisierungwerdenhiernurAnsatzemitWh=Th(Ritz-Galerkin-Verfahren) h)+(v0h; h)+a(u0h; h): (2.13) 

ArbeitfurdieZeitdiskretisierungmitdemCrank-Nicolson-Verfahrenverwendet. denierenunddieLosungalsu1h=Piu1i'i(x)darstellen,wobeidiefu1igNh bilden.TestetmannunmiteinerderFunktionen WegenderEndlichdimensionalitatderRaumekannmaneineendlicheBasisf'i(x)gNh Xiu1i('i;'j)+Xiu1ia('i;'j)=fj; h='j,soerhaltmandieGleichung 1denLosungsvektor 1vonWh

2.3.VOLLDISKRETISIERUNGINEINEMSCHRITT mitderaus(2.13)entstandenerrechterSeitefj.DaesNhlinearunabhangigeTestfunktionengibt, gibtesauchgenausovieleGleichungen,soda(2.13)aquivalentzumlinearenGleichungssystem11 

ist,mitdenMatrizenMij=('i;'j)undAij=a('i;'j)unddenVektorenu=fuigund linearenAlgebra,hiermitdemCG-Verfahren,dasmitdemJacobi-oderdemSSOR-Verfahren f=ffjg.DieLosungdiesesGleichungssystemserfolgtmiteinemderublichenVerfahrender (M+A)u=f 

vorkonditioniertwird.MundAsindaufgrundderSymmetriedesL2-Skalarproduktsundder Bilinearforma(;)undwegenWh=ThebenfallssymmetrischeMatrizen,sodadieLosung inderLagesein,dieGleichungssytemeerheblichezienterzulosen,konntenaberausZeitgrunden imRahmendieserArbeitnichtimplementiertwerden.DerAufbauderMatrizenMundAerfolgt abgesehenvonderGroedesProblemskeineSchwierigkeitenbereitet.Mehrgitterverfahrensollten durchnumerischeQuadratur.DieAufstellungderrechtenSeiteistinAbschnitt4.2beschrieben. mitdemKoezientenvektorv1=fv1igundderaus(2.11)entstandenenrechtenSeiteg=fgjg. DieDiskretisierungderGleichung(2.11)erfolgtganzanalogundliefertdasGleichungssystem 

stetigenFunktionengewahlt,diesichaufjedemElementKalsPolynomschreibenlassen,wobei ImRahmendieserArbeitwirdfurdenendlichdimensionalenRaumWhderRaumderglobal Mv1=g; 

injedemSummanddiePotenzdereinzelnenunabhangigenVariablenhochstensgleichrsei.Es wegenderbesserenApproximationseigenschaftengegenuberDreieckengewahltwurdenundweil siesichleichteraufdreiRaumdimensionenverallgemeinernlassen. werdenPolynomgradebisr=4verwendet.DasGebietwirdinViereckselementeaufgeteilt,die AufstellungderlinearenGleichungssystemegemademinAbschnitt4.3beschriebenenVerfahren behandelt. InderPraxiswerdenimmerRandwertefuru1undv1vorgegeben.Diesewerdenerstnachder 

IndiesemAbschnittsolleinerigoroseAbleitungderVolldiskretisierunggegebenwerden,wobei 2.3 keineReihenfolgebeiderDiskretisierungderOrts-undZeitrichtungenmehrangenommenwird. ZulosenseiwiederdasSystem(2.2) VolldiskretisierungineinemSchritt 

ut vt+0? A0uv=0 u(;0)=u0(); v(;0)=v0(); x2;t2I; 

mitA=?r(a(x)r).FurdieexakteLosungw=(u;v)geltew2W.DieexakteStruktur derLosungsraumeistkompliziertundseihiernichterortert;wirnehmenWH1(I;H1()) naru(x;t)=gN(x;t) u(x;t)=gD(x;t) x2?D@;t2I; 

H1(I;L2())an.5DadieLosungenimallgemeinengenausoglattsindwieAnfangs-undRandwerte,entsprichtdasinetwaderAnnahmestetigerRandwerteundAnfangswerteausH1()L2(), 

Testfunktiont=('; wasmitderphysikalischenAnschauungindenmeistenFallenubereinstimmt. WiruberfuhrendieDierentialgleichungineineschwacheFormdurchMultiplikationmiteiner (wt;t)+0? ar0w;10 )2W,Integrationuber=IundpartielleIntegration: 

x2?N=@n?D;t2I; 

unddamitRegularitatstransportentlangvonCharakteristikenstattndet;dieRegularitatistentlangvonCharak- 

teristikenhoheralssenkrechtdazu.DiesmathematischexaktauszudruckenistaberkompliziertundnichtThema 5DieSchreibweisemitHilbert-RaumenistdemProblemunangemessen,danichtklarwird,daInformations- 

0rt?(gN; )?NI=0; 8t2W: (2.14) 

dieserArbeit.

dieLosungderfolgendenGleichungseinsolle: 12WirsucheneineApproximationwh2WhzuwineinemendlichdimensionalenRaumWhW, 


DerTestraumThhatdieselbeDimensionwieWh,muabernichtnotwendigerweisemitihm ubereinstimmen. (wh;t;th)+0? ar0wh;10 

FurdieDiskretisierungmitdemCrank-Nicolson-VerfahreninderZeitundmitLagrange-ElementenimOrtwahlenwirdieRaumewiefolgt.SeidazuI=SnIn;In=(tn?1;tn]eine 

Bedingungen(shaperegularity)erfulle.Sei^Qr(K)derRaumderFunktionen,dieaufdemEin- 

ZerlegungdesZeitintervallsundTn=fKgeineZerlegungvoninVierecke,diedieublichen heitselement^K=[0;1]dpolynomialbiszur(Bi-,Tri-)Ordnungrsind,d.h.diesichgema û=X maxiircx=8>: ::: c0+c10x+c01y+c11xy+c20x2+ c +c21x2y+c12xy2+c02y2+c22x2y2furr=2;d=2, furr=1;d=2, 

0rth?(gN; h)?NI=0; 8th2Th:(2.15) 

von^Qrunterder(bi-,tri-)linearenTransformationvonderEinheitszelle^KaufdieZellender vonPolynomeninxundymitjeweilsderOrdnungrschreiben.SeiauerdemQr(Tn)dasBild miteinemMultiindexundKoezientencdarstellenlassen;alternativlassensiesichalsProdukt TriangulationTn;daimRahmendieserArbeitkeinekrummlinigberandetenGebietebetrachtet werden,istdieseTransformationausreichend.DamitdenierenwirAnsatz-undTestraum: Wh=wh=(uh;vh):wh(x;t)stetig; wh(;t)jIn2?Qr(Tn)[Qr(Tn?1)2; wh(x;t)jInlinearint; wh(;tn)2(Qr(Tn))2; uh=gDauf?D ; (2.16) 

Th=th=('h; h):th(;t)stetigauf; th(x;t)jInkonstantint; 

whmuimInnernderZeitintervalleausderVereinigungzweierFinite-Elemente-Raumekommen, th(;t)jIn2(Qr(Tn))2; 'h=0auf?D: (2.17) 

wasweiteruntenbeiderBehandlungvonhangendenKnoteninderZeiterlautert. 

kleinerwerdenderGitterweitewieetwah?1zu,dieWellenlangebetragtfurlineareElementezwei Experimente,dadasProblemdannnichtL2-stabilistundOszillationenamRandauftreten, sobaldeineWellediesentrit(vgl.Abbildung2.3).DieAmplitudederOszillationennimmtmit werteauerdennaturlichinderFormulierungenthaltenenbenotigt.Allerdingszeigennumerische AusderFormulierung(2.14)konntemanannehmen,dadieGeschwindigkeitvkeineRand- 

Gitterabstande.DiefehlendeL2-Stabilitatbeinhaltet,dadasProblemauchinderEnergienorm istebenfallsvonderOrdnungh?1.InderAuslenkungusindkeineInstabilitatenerkennbar. wobeidieZeitableitungmitdemgleichenVerfahrenwiebeiderganzenGleichungdiskretisiertsei. Entsprechendmu(2.17)um instabilist,wieinAbbildung2.4untenzusehenist;dieAmplitudederInstabilitatinderEnergie 

zuerhalten,wahlemanthso,daesauerhalbvonInverschwindeundinnerhalbkonstantsei. DieInstabilitatenverschwinden,wennmanfurvhauf?DdieBeziehungvh=@tgDfordert, 

DawhstetigundlinearinderZeitseinsollte,giltmit(2.15)furalleth=('h; UmausderFormulierung(2.15)unddenRaumen(2.16)und(2.17)einZeitschrittverfahren h=0auf?Derweitertwerden. 

?wnh?wn?1 h;th+kn20? ar0?wnh+wn?1 h;10 0rth?(gN; h)2(Qr(Tn))2 h)?NI=0: (2.18)

2.3.VOLLDISKRETISIERUNGINEINEMSCHRITT 13 

v 

v 

20 

20 

15 

15 

Abbildung2.3:VergleichderGeschwindigkeitenvohne(links)undmit(rechts)Behandlungder 

10 

10 

5 

5 

Randwertefurv. 

0 

0 

-5 

-5 

-10 

-10 

-15 

-15 

-20 

-20 

10 

8 

4 globale Verfeinerungen 





Abbildung2.4:VergleichderEnergieverlaufeohne(links)undmit(rechts)BehandlungderRandwertefurdieGeschwindigkeitv. 

10 

8 


Energie 

6 

4 

Energie 

2 

2 

0 

0 

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 

VerfahrensemidiskretisiertenGleichungen(2.4). DasistwiederdieOrtsdiskretisierungmitnitenElementendermitdemCrank-Nicolson- 

Zeit 

Zeit 

und(2.15)dieGalerkin-OrthogonalitatfurdenFehlere=w?wh DaThW,gilt(2.14)auchfuralleth2ThundwirerhaltendurchSubtraktionvon(2.14) 

diewirfurdieFehlerschatzungbenotigenwerden. (et;th)+0? ar0e;10 0rth=0; 8th2Th; (2.19) 

2.3.1HangendeKnotenimOrt DerindieserArbeitverfolgteAnsatzzurAdaptivitatverwendetGitter,beidenenZellenregular verfeinertwerden,ohnedadieentstehendenKnotenaufdenKantenaufdernachstenZelle durchsogenannte"Abfangzellen\zuregularenKnotengemachtwerden.DerGrunddafurist,da dieKonstruktionvonAbfangzellenaufVierecksgitternverhaltnismaigkompliziertistundda diemitdemverwendetenVerfahrenentstehendenGittergutfurMehrgitteralgorithmengeeignet mitihnenspezielleBasisfunktionen.DazugibtesimwesentlichendreiMoglichkeiten: (vgl.[4,22]);imRahmendieserArbeitwurdedavonallerdingskeinGebrauchgemacht. NichtkonformerAnsatz:mandeniertdieBasisfunktionenwieublichzellweiseundnimmt StattdessenbelassenwirdiehangendenKnotenimGitter(vgl.Abbildung2.5)undassoziieren dieeventuelleUnstetigkeitanderGrenzachezwischenZelle1unddenZellen2und3 inKauf.GegegebenenfallskannmaneinenStraftermfurdieUnstetigkeitindieschwache Formulierungeinfugen.DieserAnsatzfuhrtindenmeistenFallenzueinemnichtkonformen Ansatzraum. 

6 

4


2 

3 

1 3 

AssoziationeinerBasisfunktionaufdenZellen1bis3zumKnoten3.DadurchisteinstetigerAnsatzraumgewahrleistet;aufdenZellen2und3sinddieBasisfunktionenwieublich, 

Abbildung2.5:EinfachesGittermithangendemKnoten. 

2 

1 

aufderZelle1isteinespezielleBasisfunktionzuwahlenunddieBasisfunktionenzuden Knoten1und2sindentsprechendzumodizieren.DieserAnsatzhatdieNachteile,da plementationeinesMehrgitterverfahrenserschwert,unddadieBasisfunktionenaufeiner dieBasisfunktionendesfeinenGebietsbisindasgrobeGebiethineinreichen,wasdieIm- 

EliminationderBasisfunktionzumKnotendrei.DieserWeghatdenVorteil,dadieBasisfunktionenweiterhinzellweisedeniertwerdenkonnen,wieaufregularenGitternublich 

ZelleunterUmstandenvondenNachbarnabhangen,waseinenerhohtenalgorithmischen Aufwandbedeutet. 

Ansatz-undTestraumsnotigist.DieBasisfunktionkannnachAufbauderMatrizenund unddadaherpraktischkeinzusatzlicheralgorithmischerAufwandbeiderVerwaltungdes IndervorliegendenArbeitwurdederdritteWeggewahlt;dieDetailsderImplementationundder EliminationderBasisfunktionenzuhangendenKnotensindinAbschnitt4.4zunden. Vektoreneliminiertwerden. 

2.3.2HangendeKnoteninderZeit UmdieglobaleStetigkeitdesAnsatzraumeszugewahrleisten,istesnotig,hangendeKnotenin derZeitgeeignetzuinterpretieren.UntereinemhangendenKnoteninderZeitseidabeieinKnotendesortlichenGittersverstanden,derimvorhergehendenodernachfolgendenZeitschrittnicht 

mitfolgendenUnterschieden: vorhandenist.ImwesentlichenstehenwiederdiegleichenMoglichkeitewieobenoen,allerdings NichtkonformerAnsatz:indiesemFallistderAnsatzrauminderZeitunstetigundman 

AssoziationeinerBasisfunktionzudiesemKnoten.DiesistderWeg,derhierbeschritten mudasZeitschrittverfahrenumSprungtermeerganzen;dasistfurdieunstetigenGaler- 

kin-Verfahren(DG(r))zurZeitdiskretisierungublich,imRahmendesCrank-Nicolson- Verfahrensabernichtnotig. 

mussen;Basisfunktionen,dieaufeinemderbeidenEndpunktedesIntervallskeinenKnoten werdensoll.Erlauftdaraufhinaus,dadieBasisfunktionenimInnernderZeitintervalleals stetigerUbergangzwischendenBasisfunktionenderdiskretenZeitpunktebetrachtetwerden 

EliminationderBasisfunktion.DieserWegistebensomoglichwiederobige,verlangtjedoch deranderenSeite.DasZeitschrittverfahrenbehaltseineFormbeiundmunichtmodiziert haben,werdenaufdieserSeitealskonstantNullangenommen,lebenaberimInnerenundauf werden. 

ArtKopplungenzwischenmehralsnurzweiaufeinanderfolgendenZeitschritteneingefuhrt eineexpliziteBehandlungderBasisfunktionenzuhangendenKnoteninderZeitundbedeutetdamitzusatzlichenalgorithmischenAufwand.Insbesondereistschwierig,daaufdiese 

werden;manmudabeinebendemletztenauchaufdenvorletztenZeitschrittzugreifen,was denVorteilderUmschreibungzueinemSystemersterOrdnunginderZeitzunichtemachen

2.4.FEHLERKONTROLLE wurde.DergroereNachteilistjedoch,dadieserKnotenjaextraeingefugtwurde,um einehohereAuosungzuerzielen,jetztabererstabdemnachstenZeitschrittzurVerfugung 15 

steht;wahrenddasbeiderVerfeinerungimOrtwegenderrelativgroenVerfeinerungsgebietehinnehmbarist,isteshierstorenderundwegenderVorteiledeszweitenWegesnicht 

Gleichung(2.18)enthaltzweimiteinandergekoppelte,endlichdimensionaleGleichungssystemefur 2.3.3EntkopplungderGleichungen empfehlenswert. 

unhundvnh,diemanerhalt,wennmanmitth=('h;0)undth=(0; ?vnh?vn?1 ?unh?un?1 h;'h?kn2?vnh+vn?1 h;'h=0; h)testet: 

Danach(2.17)derRaumder h; h+kn2?ar(unh+un?1 

dannzweientkoppelte,nacheinanderlosbareGleichungen: betrachtet,nach(vnh;'h)auosenunddasResultatindieersteGleichungeinsetzen.Manerhalt hdie'henthalt,kannmandiezweiteGleichung,fur h);r h?(gN; h)?NI=0: 

(unh;')+k2 4(arunh;r')=?un?1 h;'+kn?vn?1 h='h 

(vnh; h)=?vn?1 ?k2 h; 4?arun?1 h?kn2?ar(unh+un?1 h;r'+k2(gN;')?NIn; h;' 

DieseUmordnungistanalogzurBildungdesSchur-KomplementseinesBlock-Gleichungssystems. DieersteGleichungisteineHelmholtz-Gleichungmit"gutartigem\Vorzeichen;sieverursacht denmeistennumerischenAufwandbeimLosen.DiezweiteGleichungistnurnocheineL2- h);r h+(gN; h)?NI: 

Projektion,diemitgeringemAufwandzulosenist. nichtmoglichist,dieersteindiezweiteGleichungeinzusetzen,daderRaumder'hkleineralsder der dieumgekehrteEinsetzungistmoglich;siebringtaberauereinereingespartenMatrix-Vektor- MultiplikationproZeitschrittkeinenVorteil. VerwendetmandieursprunglicheDenitionderAnsatz-undTestraume,soistklar,daes 

furdasFractional-Step--Verfahrenganzanalogmoglich. DiebeschriebeneEntkopplungderbeidenGleichungenistfurdasallgemeine-Verfahrenund hist.FordertmandiezusatzlichenRandbedingungen,sosinddiebeidenRaumegleichund 

IndiesemAbschnittsolleinaposterioriFehlerschatzerfurdenFehlerzwischenderexaktenund 2.4 dernumerischenLosungbezuglicheinesbeliebigenFunktionalshergeleitetwerden.DieserSchatzer sollausschlielichdienumerischeLosungverwenden,sodaerdenFehlerwirklichschatzenkann Fehlerkontrolle 

undnichtwiedieklassischenFehlerindikatorenaufgrundderAbhangigkeitvonderunbekannten exaktenLosungdenFehlernuranzeigenkann. Crank-Nicolson-unddasFractional-Step--VerfahreninFrage.DadieHerleitungdesFehlerschatzersdaraufberuht,dasichdieDiskretisierungderGleichungalsGalerkin-Verfahredenwerden. 

AufgrundderErgebnisseaus2.1kommenunterdenbetrachtetenZeitschrittverfahrennurdas schreibenlat,kannaufdiesemWegnureinSchatzerfurdasCrank-Nicolson-Verfahrengefun- 

sonderneinedarausberechneteGroe.ImKontextderWellengleichungkonntendasbeispielsweise 2.4.1VorbemerkungenundNotationen InderPraxisinteressiertaneinergefundenenoderberechnetenLosungoftnichtdieLosungselbst,

dieEnergiezueinemZeitpunktT 16 KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

derintegrierteEnergieudurcheineKurveC E(u)=12[(ut(;T);ut(;T))+a(u(;T);u(;T))]; 

FehlerindieserGroe;esistalsobeispielsweisezugarantieren,dajE(u)?E(uh)j

2.4.FEHLERKONTROLLE odernachineinandereinsetzen 17 

welchenGewichteneinRaum-Zeit-PunktzumErgebnisJ(w)beitragt.End-undRandwertefur erfullt.6DieseWellengleichungistinderZeitruckwartszulosen;ihreLosungbeschreibt,mit wsinddurchdieunterUmstandensingularenGewichtejgegeben;manbeachteauchdieVertauschungderRollenvonuundv. 

vtt?rarv=j1?j2;t (2.21) 

MitderGalerkin-Orthogonalitat(2.19)latsicheinbeliebigeswh=(uh;vh)2Theinschieben:7 AufgrunddesdualenProblemsgiltfurdenFehlerinderZielgroe 

J(e)=(et;w?wh)I+b(e;w?wh) J(e)=(et;w)I+b(e;w): 

=NXn=1X=0;wegen(2.14) =(wt;w?wh)I+b(w;w?wh) | 

K2Tn~EK;n{z }?(wh;t;w?wh)I?b(wh;w?wh) 

~EK;n=n?(wh;t;w?wh)KIn+(vh;u?uh)KIn UmdieseFehleridentitatauchalsIndikatorzurGitterverfeinerungverwendenzukonnen,muder Fehlerbesserlokalisiertwerden;diesgeschiehtdurchpartielleIntegrationdesdrittenTerms,so ?(aruh;r(v?vh))KIn+(gN;v?vh)(?N\@K)Ino: 

dawirmitderDenitioneinesSprungterms 

wobeiJdaszuKbenachbarteElementmitgemeinsamerSeitesei,schreibenkonnen: [naruh]=8

mandenobigenIndikator~EK;nbeispielweisefureineimInnernvongelegeneZelleKpartiell integriert: 18 KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

wobeiJwiederdiejeweilszuKbenachbarteZellesei.ImGrenzfallh!0gehtderSprungterm ~EK;n=EK;n?12(na(ruhjK+ruhjJ);v?vh)@KIn; 

inEK;ngegenNull,wogegenderersteFaktorimletztenTermderletztenGleichunggegenetwas Konstantesgeht. ist.Um(2.22)dochnochauswertenzukonnen,gibtesjedochverschiedeneMoglichkeiten(fur statischeProblemevergleiche[6]),dieimfolgendendiskutiertwerdensollen. DieDarstellung(2.22)istnochnichtsehrhilfreich,dadieexaktedualeLosungwunbekannt 

ErsetztmandieexaktedualeLosungwdurcheineApproximation,diemanausdernumerischen LosungdesdualenProblemserhalt,solatsichdieFehleridentitatnaherungsweiseauswerten.Es 2.4.3AuswertungmithoheremAnsatzgrad 

zuberechnen,dasichdannderFehlerdurchWahlvonwh=w(r) reichtdabeinichtaus,diedualeLosungmitdemgleichenVerfahrenwiedasprimaleProblem 

aufjederZelle,abergleicherOrdnunginderZeitundaufdemgleichenOrts-Zeit-Gittererhalten ausgesetzt,w(r) manaberwdurcheinenumerischeLosungw(r+1) hliegtinTh),wasnaturlichkeinensinnvollenFehlerschatzerergabe.Approximiert h ,diemiteinemumeinshoherenPolynomgrad hzuNullauswertenliee(vor- 

wurde,solatsichdieFehleridentitat(2.22)naherungsweiseauswerten.Furwhsetzenwir 

d.h.dieInterpolationaufdenAnsatzraumdesprimalenProblems.Manbeachte,dawhauf whjIn=12I(r) hw(r+1) h (tn?1)+w(r+1) h (tn); 

jedemIntervallIninderZeitkonstantseinmu,dawh2Th.DieWahlderInterpolationanstatt derProjektionaufdenniedrigerenPolynomraumistnichtoptimal;dasgiltvorallemfurr=1, daindiesemFallw(r+1) negativeFunktionistundwirsomitWeghebungseektedurchwechselndeVorzeichenaufeiner Zelle(wiewirsiebeispielsweisedurcheineProjektionerhaltenkonnten)nichtnutzenkonnen.Der GrundfurdieWahlderInterpolationliegtdarin,dawhstetigimOrtseinmuunddawirdas h ?wh(;t)furfestestaufjederZelleentwedereinepositiveoder 

durchlokaleInterpolationaufjederZelleerreichenkonnen,nichtjedochdurcheineProjektion.Es FehlerschatzerszurGittersteuerungnochzuoptimieren. stantinderZeitsind.w(r+1) wurdekeinVersuchunternommen,durchglobaleoderpatchweiseProjektiondieVerwendungdes ZurAuswertungdesFehlerschatzersbeachtenwir,dawh;tundwhaufjedemIntervallkon- 

wurde.DiegleicheAnnahmegeltefurgN.ManerhaltdannfurdieeinzelnenTermevon(2.22) diefolgendenAusdrucke(dieSuperskripte(r+1)anw(r+1) exakt,fallsdiew(r+1) (dasentsprichtderAuswertungdesZeitintegralsmitderTrapezregel);dieseAnnahmeistsogar h durchZeitdiskretisierungmitdemCrank-Nicolson-Verfahrenerhalten h wirdalsaufjedemZeitintervallalslinearinderZeitangenommen 

PlatzfurdiedenZeitschrittbezeichnendenSuperskriptezuhaben;allewhaufderrechtenSeite h seienimfolgendenweggelassen,um

2.4.FEHLERKONTROLLE 19 

sindinWirklichkeitw(r+1) 

h ): 

?(wh;t;w?wh)KIn=?ZInwnh?wn?1 

h 

k ;w(r+1) 

h (t)?whKdt 

?(wnh?wn?1 

h);12(1?I(r) 

h)(wnh+wn?1 

h)K; 

(vh;u?uh)KInk(14(vnh+vn?1 

h);(1?I(r) 

h)(unh+un?1 

h)K 

+112?(vnh?vn?1 

h);unh?un?1 

hK); 

(raruh;v?vh)KInk(14rar(unh+un?1 

h);(1?I(r) 

h)(vnh+vn?1 

h)K 

+112?rar(unh?un?1 

h);vnh?vn?1 

hK) 

=k(14a(unh+un?1 

h);(1?I(r) 

h)(vnh+vn?1 

h)K 

+112?a(unh?un?1 

h);vnh?vn?1 

hK) 

+k(14(ra)r(unh+un?1 

h);(1?I(r) 

h)(vnh+vn?1 

h)K 

+1 

12?(ra)r(unh?un?1 

h);vnh?vn?1 

hK); 

?12([naruh];v?vh)@KIn?k2(14[nar(unh+un?1 

h)];(1?I(r) 

h)(vnh+vn?1 

h)@K 

+1 

12?[nar(unh?un?1 

h)];vnh?vn?1 

h@K): 

DieeinzelnenTermewerdenmiteinerQuadraturformelderOrdnungr+2ausgewertet.Derdritte 

TermistfurallgemeineGitteretwaskompliziert,dabeiderTransformationderzweitenAbleitung 

aufdieEinheitszelleAbleitungenderJacobi-MatrixunddesKoezientenauftreten;dieselassen 

sichaberapriorialsFunktionderEckpunktederZellenangeben,sodadieAuswertungohne 

numerischeDierentationmoglichist. 

DieAuswertungdereinzelnenTermeistauchdannmoglich,wenndieZelleKzwischentn?1 

undtnvergrobertoderverfeinertwurde;dasVerfahrenistanalogdeminAbschnitt4.2beschriebenen,jedochkomplizierter.InsbesondereistdieAuswertungbeiVergroberungprogrammtechnisch 

ausgesprochenaufwendig,wasanderAnwendungderInterpolationI(r) 

hwn?1liegt;dadieInterpolationaufdenTestraumQr(Tn)durchgefuhrtwerdenmu,kannsiebeiVergroberungnichtauf 

denkleinenZellendesaltenGittersgeschehen,aufdenenwn?1deniertist,sondernnuraufder 

entsprechenden,groberenZelledesneuenGittersundistsomitnichtlokal,wasdieProgrammierung 

erheblichkompliziert.Zubeachtenistauch,daimFallederVergroberungdieGradientenimInnerneinerRaum-Zeit-ZelleKIn,K2Tn,unstetigseinkonnen,sodazusatzlicheSprungterme 

auftreten. 

DieVerfeinerungvonZellenistdagegeneinfachzubehandeln,dadieAuswertungderInterpolationaufgrundderEinbettungderRaumeaufdenjeweilskleinstenZellendurchgefuhrtwerden 

kann.

derobigenWahlvonwhdiefolgendeInterpolationzunehmen: 20AufgrunddergeschildertenProblememitdemTermI(r) 


whjIn=I(r) hw(r+1) h (tn): hwn?1erscheintesnaheliegend,statt 

lerschatzerlokalnichtdiemaximaleOrdnungzeigt(esfehlteinek-Potenz),sodadieerzeugten GitterunterUmstandennichtoptimalsind. DadurchlassensichdiegeschildertenProblemeumgehen,allerdingsumdenPreis,daderFeh- 

Schreibtman(2.22)etwasum,soerhaltman EinfacheAbschatzung 2.4.4AbschatzungmitdemBramble-Hilbert-Lemma 

EK;n=??uh;t?vh | {z r1 };u?uhKIn??vh;t?raruh 

| {z r2 ?12([naruh];v?vh)@KIn };v?vhKIn 

DieerstenbeidenTermesindResiduenterme,derletztemitdieGlattheitdernumerischenLosung. (2.23) 

DiesschatztmannunmittelsderCauchy-SchwarzschenUngleichungab: 

jEK;njkr1kKInku?uhkKIn+kr2kKInkv?vhkKIn jJ(e)jNXn=1X 

+12k[naru]k@KInkv?vhk@KIn: K2TnjEK;nj; 

WirwollendenFehlersoscharfwiemoglichabschatzenundversuchendaher,einwh2Thnahean derexaktendualenLosungwzuwahlen,alsozumBeispieldieInterpolationwhjIn=I(r) oderdieProjektionwh=Thw. LemmaundeinerErweiterungfurPolynomemitunterschiedlichemGradinOrts-undZeitrichtung (siehezumBeispiel[7]und[19])wiefolgtabschatzen:9 ImFallederInterpolationlassensichdieTermemitw?whmitdemBramble-Hilbert- hw(tn?1) 

ku?uhkKInCknkutkKIn+kr+1 

tuKIn+hr+1 

kv?vhk@KInCh?12 kv?vhkKInCknkvtkKIn+kr+1 K?kv?vhkKIn+hKkr(v?vh)kKIn n@r+1 tvKIn+hr+1 Krr+1vKIn; Krr+1uKIn; 

istallerdingsoftwenigergegeben,insbesonderebeilokalisiertenFehlerfunktionalen(Kantenintegrale,Punktauswertungen).DieAbschatzungenbleibenimwesentlichengultig,wennmandie 

K?knkvtkKIn+knhKkrvtkKIn: HinreichendeGlattheitvonw,z.B.w2Hr+1([0;T])wurdehiervorausgesetzt;inderPraxis 

derh-undk-Potenzenentsprechenderniedrigt.DaindernumerischenPraxisdieexakteduale nichtmehrexistierendenAbleitungendurchniedrigereAbleitungenersetztunddenExponenten zenquotientenersetztwerden,verlierendieobigenAbschatzungenihrenWertnichtundesseian dieserStelleaufdieUnubersichtlichkeitderVerallgemeinerungauffehlendeRegularitatverzichtet. LosungwohnehindurcheineaufnumerischemWegerhaltene,sowieAbleitungendurchDieren- 

gradedesdiskretenTestraumsThinderZeit-unddenbeidenOrtsrichtungen.Mitderublichenshaperegularity- BedingungandasGitterkannmandieAbleitungeninx-undy-Richtungzusammenfassenunderhaltnurnoch TermemithKstatthxundhy.FurdendrittenTermverwendemandenSpursatz. 9ManverwendefurdieerstenbeidenUngleichungen[19,Satz2.3.7]mit=(0;r;r).bezeichnetdiePolynom-

2.4.FEHLERKONTROLLE Fehlerschatzergema UnterderAnnahme,dadieAbschatzungeninderobigenFormgultigsind,latsichein 21 

K;n=hdKkn1;k =CNXn=1X K2TnK;n 

mitdenResiduenundGewichten K;n!1;k K;n+1;h K;n!1;h K;n+2;k K;n!2;k K;n+2;h K;n!2;h K;n+3K;n!3K;n; (2.24) 

!1;k 1;k 

K;n=h?d=2 Kk1=2 Kk?1=2 nkr1kKIn; 

kutkKIn+krn@r+1 

!1;h 1;h K;n=hr+1 

n1;k K;n=hr+1?d=2 K k?1=2 n tuKIn; 

2;k 

Kk?1=2 Kk1=2 

rr+1uKIn; kr1kKIn; 

!2;k K;n=h?d=2 Kk?1=2 nkr2kKIn; n kvtkKIn+krn@r+1 

!2;h 2;h K;n=hr+1 

n2;k K;n=hr+1?d=2 K k?1=2 ntvKIn; 

3K;n=12h?d=2n K;n=h?d=2 Kk?1=2rr+1vKIn; 

kr2kKIn; 

denieren;dbezeichnedieRaumdimension.EsistausderHerleitungoensichtlich,dajJ(e)j, !3K;n=h?d=2 Kk?1=2 Kk1=2 n nk[naru]k@KIn; 

d.h.dawirnutzenkonnenumdieGroedesFehlersnachobenhinzugarantieren.DieVorfakten ?kvtkKIn+hKkrvtkKIn; derGewichte!iK;nwurdensogewahlt,dasiefurhK;kn!0gegenkontinuierlicheFunktionen gehen;dergemeinsameFaktorhdKknwurdeausdenGewichtenundResiduengezogen,damitdie 

Thangewendethaben,wahrenddiequadratischek-OrdnungimRaumWhliegt.EinAnsatz,die liegthierdarin,dawirdieBramble-Hilbert-AbschatzungaufElementederTestraumeTund suboptimal,dadieKonvergenzordnungdesCrank-Nicolson-VerfahrensO(k2)ist;dasProblem SummeimerwahntenGrenzfallgegeneinIntegralgeht. 

OrdnungdesFehlerschatzersderdesProblemsanzupassen,wirdimnachstenAbschnittskizziert. DurchAufsummationerhaltmaneineglobaleOrdnungvonO(k+hr+1).Dasistoensichtlich 

d.h.1und2gegenuberdemKantenterm3vonhohererOrdnungsindunddaherimLimes vernachlassigtwerdenkonnen[30].VerwendetmannocheineaprioriStabilitatsabschatzungder dualenLosungderForm!3CS(k;u),wasbeiderAbschatzungdesEnergiefehlersimallgemeinen moglichist,soerhaltmaneinenSchatzerderForm(2.9),wasseinead-hocVerwendungplausibel FurElementemitungerademAnsatzgradistbekannt,dadieTermemitdemZellresiduum, 

GetrennteAbschatzungfurZeit-undOrtsgitterweite macht. MankanndasebenbeschriebeneProblemderfalschenKonvergenzordnungumgehen,wennman aufdasCrank-Nicolson-Verfahrenzunden. Ansatzseihiernurkurzskizziert,Detailssindin[6]furstatischeundin[19]furdieAnwendung stattderInterpolationwh=I(r) hweineInterpolationmitProjektionscharakterwahlt.Dieser


DurchdieseWahlvonwhlatsichdanebenaucheineTrennungderh-undk-Potenzenin 

denBeitragenzuK;nerreichen,vergleiche[7,19],womitesmoglichist,dieFehler,diedurchdie 

Orts-bzw.Zeitdiskretisierungentstanden,zutrennen.Dadurchistesmoglich,lokaleVerfeinerung 

inOrtundZeitunabhangigvoneinanderadaptivdurchzufuhren,jenachdem,welcherTeildes 

FehlerschatzersdengroerenBeitragliefert. 

ZurHerleitungeinesentsprechendenFehlerschatzersverwendenwirdieInterpolationmitProjektionseigenschaften~ITaus[19],diefolgendeEigenschaftenhat:10 

Esgelte~IT=~I(1) 

hP0In,wobeiP0IndieProjektioninderZeitaufstuckweisekonstanteFunktionenund~I(1) 

hdieimfolgendenbeschriebeneInterpolationimOrtist. 

ZurDenitionderInterpolationimOrtunterteilenwirdasGebietsoinMakrozellen 

~K,dajedeMakrozellegenaueinmalverfeinertwerdenmu,umzumfeinstenGitterzu 

kommen.JederZelleKlatsichsoeindeutigeineMakrozelle~Kzuordnen,diesozusagen 

ihreMutterzelleist. 

DerEinfachheithalberbeschrankenwirunsinderfolgendenBeschreibungaufzweiRaumdimensionen.JedeMakrozellebestehtdortausvierKindzellenundumfatsomit9Knoten. 

DieInterpolationistnunsodeniert,dasieindenvierEckpunktendenPunktwertderzu 

interpolierendenFunktionauswertet,denvierSeitenmittenderMakrozelledenMittelwert 

derbeidenumliegendenEckpunktezuordnetunddemKnoteninderMitteeinensolchen 

Wertzuweist,dadieDierenzzwischeneinerbeliebigenFunktionundihrerInterpolierendendenMittelwertNullhat: 

u?~I(1) 

hu;'~K=0 8'2P0(~K): (2.25) 

DieseletzteEigenschaftverleihtderInterpolationeinenProjektionscharakter,daderFehler 

senkrechtaufdemRaumderFunktionensteht,dieaufjederMakrozellekonstanteWerte 

haben. 

ImInnerenjederdervierZellenderMakrozelleistdieFunktiondiebilineareFunktionmit 

denobendeniertenWertenindenKnoten. 

DieErweiterungaufbeliebigeRaumdimensionenistoensichtlich;aufgrundderKonstruktionuberMakrozellenpatsichdieInterpolationnaturlichindasUmfeldadaptivverfeinerter 

Gitterein. 

FurweitereDetailssiehe[19,Abschnitte2.4.1bis2.4.3].DieWahldieserrelativkompliziertenInterpolationistnurfurdieAbschatungrelevant,siemunichttatsachlichausgewertetwerden.Diese 

Interpolationwurdesogewahlt,dasiedieVorteilederInterpolation(lokaleFehlerabschatzungen) 

undderProjektion(derFehlerstehtsenkrechtaufbestimmtenRaumen)insichvereint. 

MitdersodeniertenInterpolation~ITlatsichnunwiedereinFehlerschatzerherleiten,wie 

amerstenZellresiduentermin(2.23)demonstriertsei.DazuspaltenwirzuerstineinenOrts-und 

einenZeitanteilauf: 

r1;u?~ITuKIn=?r1;u?P0InuKIn+r1;P0Inu?~ITuKIn: 

DiebeidenTermewerdennunnacheinanderbehandelt.ImerstenTermbeachtenwirdader 

FehlerderProjektionP0InsenkrechtaufdemRaumP0(In)stehtunddieStabilitatderProjektion 

10In[19]istdieInterpolationfurbeliebigePolynomgradedesTestraumsbeschrieben.Dawirhierabernuran 

einemFehlerschatzerfurdasCrank-Nicolson-Verfahreninteressiertsind,giltdasfolgendenurfurdenSpezialfall 

inderZeitstuckweisekonstanterTestfunktionen.DainderzitiertenArbeitnurbilineareElementeuntersucht 

werden,seiendieseauchimfolgendenverwendet;dieErweiterungaufhohereAnsatzgradeistoensichtlich,aber 

technisch,undseihierdeshalbunterlassen.

2.4.FEHLERKONTROLLE P0InuInCkukIn: ?r1;u?P0InuKIn=?r1;u?P0InuKIn 

23 

?r1;u?P0InuKInZKr1?P0Inr1Inu?P0InuIndx =?r1?P0Inr1;u?P0InuKIn 

FurdenzeitenSummandenobengilteinerseits Cknminkr1kKIn;knk@tr1kKIn CZKminkr1kIn;knk@tr1kIn knk@tukIndx 

r1;P0Inu?~ITuKInZInkr1kK(1?~I(1) h)P0InuKdt; k@tukKIn: 

andererseitsaberaufgrundderProjektionseigenschaft(2.25): XK2~Kr1;P0Inu?~ITuKIn=r1;P0Inu?~ITu~KIn =r1;(1?~I(1) =r1?~r1;(1?~I(1) =ZInr1?~r1;(1?~I(1) h)P0Inu~KIn h)P0Inu~KIn wobei~r1einbeliebigesElementausP0(~KIn)sei.Wirwollen~r1alsInterpolationvonr1auf diesenRaumauassen;dadieserjedochnichtaufK,sondernauf~Kdeniertist,kannman~r1 h)P0Inu~Kdt; 

Patchesan,d.h.r1;P0Inu?~ITuKIn2?dXK2~Kr1;P0Inu?~ITuKIn; 

nichtlokalausr1berechenundeskannaufKkeineAbschatzungenderNormvonr1?~r1geben; dasIntegrationsgebietmutedaheraufdenganzenPatcherweitertwerden. NimmtmannuneinenaherungsweiseGleichverteilungderFehleraufdeneinzelnenZelleneines 

sogiltr1;P0Inu?~ITuKInZInminkr1kK;2?dkr1?~r1k~K undwirerhaltenmitdemBramble-Hilbert-Lemma (1?~I(1) 

kr1?~r1k~KCh~Kkrr1k~K; h)P0InuKdt; 

Damitgiltinsgesamt (1?~I(1) h)P0InuKCh2~Kr2u~K: 

r1;u?~ITuKInC1kn?minkr1kKIn;knk@tr1kKIn +C2h2~Kminkr1kKIn;h~Kkrr1k~KIn k@tukKIn 

denSprungenaufdenZellkanten,beidemdurchdieVerwendungdesSpursatzeseineVermischung DieAuswertungderanderenTermein(2.23)erfolgtanalog;damanauerimSummandenmit r2u~KIn:

derPotenzenverursachtwird,jeweilszweiTermebekommt,vondeneneinernurk-,derandere nurh-Potenzenenthalt,latsichdurchVergleichfeststellen,obeineVerfeinerungdesOrts-oder 24 KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

desZeitgittersdieGenauigkeitmehrerhohenwird. InsgesamterhaltmanalsFehlerschatzerdiefolgendenAusdrucke: 

K;n=hdKkn3Xs=1s;k jJ(e)jCXnX K;n!s;k K2TnK;n; 

mitdenResiduenundGewichten 1;k 

K;n+s;h K;n!s;h 

Kk1=2 K;n; (2.26) 

!1;k 1;h K;n=h?d=2 K;n=h2?d=2 Kk?1=2 

k@tukKIn; minkr1kKIn;knk@tr1kKIn ; 

!1;h K 2;k 

Kk1=2 Kk?1=2 

nr2u~KIn 

minkr1kKIn;h~Kkrr1k~KIn ; 

!2;k 2;h K;n=h2?d=2 K;n=h?d=2 Kk?1=2 

k@tvkKIn; minkr2kKIn;knk@tr2kKIn ; 

!2;h 

3;k K;n=h?d=2?1=2 

Kk?1=2 

nr2v~KIn; 

minkr2kKIn;h~Kkrr2k~KIn ; 

!3;k K k1=2 

3;h 

K;n=12h3=2?d=2 Kk?1=2 n ?k@tvkKIn+hKk@trvkKIn; mink[naruh]k@KIn;knk[@tnaruh]k@KIn ; 

DieSkalierungderGewichte!undderganzenSummewurdenwiederwieobengewahlt,d.h.so, !3;h K;n=!2;h K;n: K k?1=2 n k[naruh]k@KIn; 

daimLimesh;k!0die!gegeneinekontinuierlicheFunktionunddieSummegegeneinIntegral gehen.BeiderZusammenfassungvonh-PotenzenwurdekeinUnterschiedzwischenhKundh~K gemacht,dasichdiebeidennurumeinenFaktorzweiunterscheiden;dieseKonstantewurdein dieohnehinunbekannteKonstanteCimFehlerschatzerabsorbiert.EineImplementationineinem ProgrammwirddiesenUnterschiedjedochbeachten. werdenkonnte,istnochnichtberucksichtigt,dabeiVergoberungauchimInnerenderRaum- gralenherauszunehmen. Zeit-ZellenKInunstetigeGradientenauftretenkonnen.IndiesenFallensindschonin(2.23) zusatzlicheSpungtermeeinzufuhrenunddieUnstetigkeitsmannigfaltigkeitenausdenGebietsinte- 

BeiderHerleitungdiesesFehlerschatzers,derpraktischunverandertaus[19]ubernommen 

derPraxiswirdsichdieserMangeljedochmeistnichtwesentlichbemerkbarmachen,dadieVergroberungimmernurrechtwenigeZellenbetritunddaruberhinausauchnurdie,aufdenendie 

Losungimwesentlichenglattist,d.h.aufdenendieSprungtermekleinsind.DieImplementation dieserzusatzlichenSprungtermeineinemComputerprogrammwird,ebensowiedieVerwendung InbisherigenArbeitenwurdendieseModikationennichtvorgenommenoderubersehen;in 

dernichtlokalenInterpolationbeiderAuswertungderexaktenFehleridentitat,wiesieinAbschnitt 2.4.3dargestelltwurde,erheblicheSchwierigkeitenbereiten.


2.4.5VergleichderbeidenWegederAuswertung 

ImProgramm,mitdemdieMethodendieserArbeitumgesetztwurden,wurdederWegderAuswertungdesFehlerschatzersmiteinergenauergerechnetendualenFunktiongewahlt.Dieserhat 

gegenuberderAbschatzungmitdemBramble-Hilbert-LemmadiefolgendenVorteile: 

ImPrinzipsollteesmoglichsein,dieFehleridentitat(2.22)quantitativpraktischexaktauszuwerten(dieGenauigkeitdesFehlerschatzersollteinetwaderselbenGroenordnungliegenwiederFehleraufeinemeinmalverfeinertenGitter).ImGegensatzdazusindbeider 

AbschatzungmitdemBramble-Hilbert-LemmadieInterpolationskonstantennochunbekannt.DurcheinigeanalytischeUberlegungenkannmanzeigen,dasiefurquadratische 

Zellenzwischen0.1und1liegen;durchProbierenindiesemBereichkonnensiedannso 

gewahltwerden,dasiebeieinfachenProblemen,beidenendieexakteLosungbekannt 

ist,denEzienzindexdesFehlerschatzers(d.h.dasVerhaltnisvongeschatztemzuechtem 

Fehler)aufWertenaheeinsbringen.Allerdingsistunklar,obdasdannauchbeirealen 

Problemengilt,beidenenverzerrteZellen,einspringendeEckenusw.vorkommen. 

DamiteinhergehendistdieMoglichkeit,dasVorzeichendesFehlersanzugeben.Ineinigen 

praxisrelevantenFallenkanndasvonVorteilsein,beispielsweisewennmiteinerSimulation 

gezeigtwerdensoll,daeinvorgegebenerMaximalwertnichtuberschrittenwird.Inder 

PraxisgibtderFehlerschatzerdasVorzeichendesFehlersbereitsaufrechtgrobenGittern 

immerrichtigist. 

DenangefuhrtenVorteilenstehenjedochdiefolgendenNachteilegegenuber: 

InderPraxishatessichgezeigt,dascharfeFehlerwertenurmitgroemAufwandzuerreichensind.DazutragensowohlmathematischeSchwierigkeiten,insbesonderedieLinearisierungnichtlinearerFehlerfunktionalealsauchpraktischeGrundebei,zuletzteremvor 

allemdieImplementationvonInterpolationenundVergleichenubermehrereZeitschritte 

mitunterschiedlichenGittern. 

AufdenerstenBlickerschiendieImplementationdesFehlerschatzersaufdieseArteinfacher. 

DerGrunddafurist,dabeiderAuswertungderNormenindenGewichten!iK;nAbleitungen 

auftreten,diehoheralsderAnsatzgradsind,sodasiedurchDierenzenquotientenaufdem 

KumgebendenPatchvonZellenapproximiertwerdenmussen;besondersstorendsindin 

diesemZusammenhangdiehohenZeitableitungbeiderVerwendungvonElementenmit 

hoheremAnsatzgradimOrt. 

DieseEinschatzungmujedoch,zumindestfurzeitabhangigeProbleme,aufgrundderNichtlokalitatderInterpolationrevidiertwerden,diealleinfureinenerheblichenTeilderKomplexitatderImplementationverantwortlichist. 

SchlielichistderganzerheblichhoherenumerischeAufwandzubeachten.DieBerechnung 

derdualenLosungmiteinemquadratischenstatteinemlinearenAnsatzbenotigtrundvier 

MalsovielRechenzeitund-speicherunddominiertdamitdieverwendetenRessourcenfur 

dasprimaleProblemumeinMehrfaches.DiesesVerhaltnisbessertsichzwaretwasfurhohere 

Ansatzgrade,allerdingsistnichtklar,obesimmerausreicht,diedualeLosungdannnochmit 

nurumeinshoheremAnsatzgradzurechnen.DerGrundistdermitwachsendemrkleiner 

werdendeAbstandzwischenQr(T)undQr+1(T)imVergleichzumAbstandzwischenQr(T) 

unddemkontinuierlichenLosungsraum;wirddasVerhaltnisderAbstandezuklein,wirddie 

Ersetzung (1?I(r) 

h)w ?! (1?I(r) 

h)wh 

fragwurdig. 

WieinKapitel5gezeigt,istderAufwandineinigenFallentrotzdemnurinetwaderselben 

GroenordnungwiebeiderVerwendungeineseinfachenEnergiefehlerschatzersoderbeiglobalerVerfeinerung,wofurmanimmerhineineAussageuberdieGroedesFehlerbekommt.

26DerAufwandlieesichabererheblichsenken,wennmandiedualeLosungmitdemgleichen 

AnsatzgradrechnenwurdewiedasprimaleProblem.InderPraxislieesichderzusatzliche KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

wendungdesmitdemBramble-Hilbert-LemmahergeleitetenFehlerschatzersdahersinnvoller. gerechnetenLosungdieErwartungnichterfullenkonnte.FurzukunftigeProblemescheintdieVer- 

Abschlieendmufestgestelltwerden,dadieAuswertungmiteinermithoheremAnsatzgrad Aufwandwohlkaumrechtfertigen. 

DafursprechenimwesentlichendiefolgendenArgumente: InderPraxishatessicherwiesen,daesoftnurwichtigist,dieGroenordnungdesFehlers 

FurProblemeausdemUmfeldderWellengleichung,aberauchfurvieleandereProblemeohneDampfungodermitstarkenNichtlinearitatenistderAufwandzurLosungmit 

zukennen;inkritischenFallenwirdmanohnehineinMehrfachesdesgeschatztenoderberechnetenFehlersalsSicherheitsmargenehmen,sodaeineUngenauigkeitdurchdieWahl 

derInterpolationskonstanteninvielenFallenakzeptabelist. 

derdualenLosungverwendetwurden,wederrechtfertigennochinvielenFallenbereitstellen. EinfurdiePraxiswesentlichwichtigeresKriteriumist,obeinProblemdurchdieVerwendungeinesFehlerschatzersaufeinehohereGenauigkeitbzw.uberhauptgelostwerdenkann. 

unterschieden,wennstattdembeschriebenenSchatzereinenurteilweiseimplementierte DieexaktereAuswertungdesFehlerschatzerswirddahernurunwesentlichezientereGitter leitetenSchatzers.DagegenzeigtdieErfahrung,dadieVerwendungeinesdualenProblems produzierenkonnenalsbeiderVerwendungdesmitdemBramble-Hilbert-Lemmasherge- 

invielenFallenistbeihyperbolischenGleichungendiesesGewichtNull,namentlichwenn GewichtungeinesRaum-Zeit-PunktsmitseinemBeitragzumEndergebnisverantwortlichist; eineteilweisedrastischeReduktionderbenotigtenZellenbewirkte,wofurhauptsachlichdie 

ren.IndiesenFallenlassensichdieerheblichhoherenRessourcen,diehierzurBestimmung "vernunftiger\GenauigkeitanderGrenzedesmitderheutigenRechnertechnikErreichba- 

DieErfahrungbeiderArbeitamProgrammhatgezeigt,dadieerzeugtenGittersichkaum Version(zumBeispielnurdieGebietsresiduenohnedieSprungterme)verwendetwurde. 

LetztlichistderAufwandzurImplementationdesindieserArbeitverfolgtenWeges,wenigstensfurzeitabhangigeProbleme,mindestensgenausohoch,wahrscheinlichsogarhoherals 

deranderevorgeschlageneWeg. derPunktauerhaltdesEinugebietsdesZielfunktionalsliegt. 

BeiderFehlerkontrollewarenwiraneinerAuswertungJ(w)derLosunginteressiert.J()konnte 2.4.6BewertungderLinearisierungnichtlinearerZielfunktionale dabeieinPunktwert,einIntegral,dieEnergieodereinbeliebigesanderes,nichtnotwendigerweise linearesFunktionalsein.AbzuschatzenwarderFehler 

einlinearesFunktionalJ()sogewahltwerden,da denmandurchdieAuswertungdernumerischenanstellederexaktenLosungmacht.Dazumute J(w)?J(wh); 

gilt.DierichtigeWahldafurist J(w?wh)=Z1 J(e)=J(w?wh)=J(w)?J(wh)=J(w)?J(wh) 

0J w(sw+(1?s)wh)ds(w?wh); (2.27)

2.4.FEHLERKONTROLLE d.h.dieDierenzzweierFunktionalwerteistdieIntervallangemaldermittlerenAbleitungdes FunktionalimIntervall.11DadieexakteLosungnichtbekanntist,wirdalsrechteSeitedesdualen 27 

ProblemsdasgestorteFunktional ~J(w?wh)=Z1 

gewonnenwurden. verwendet.12DieTildekennzeichneimfolgendenGroen,diemitdiesemgestortenFunktional 0J w(wh)ds(w?wh)=J w(wh;w?wh) (2.28) 

J()?~J()=Z1 DieDierenzderbeidenFunktionaleistnachdemgleichenVerfahrenwieobendurch 

0J 0Z1 w(sw+(1?s)wh)?J 02J u2(r(sw+(1?s)wh)+(1?r)wh)dr(sw+(1?s)wh?wh)ds() w(wh)ds() 

gegeben.VerwendetmandieLinearitatvon2J rsiminnerenIntegral,soerhaltmanfurdieAbweichungzwischendemgesuchtenFehlerfunktional unddemaufgrundderLinearisierungfalschlicherweiseerhaltenenWert J()=J()?~J()=Z1 0Z1 

u2inseinemzweitenArgumentundsubstituiertq= 

=Z1 =Z1 0Zs 0Zs 02J u2(qw+(1?q)wh)dq(w?wh)ds() u2(r(sw+(1?s)wh)+(1?r)wh)dr(w?wh)sds() 

J()istnuneinlinearesFunktional,sodamanwieschoninAbschnitt2.4.2gemadem RieszschenSatzeinElementj(w;x;t)desDualraumsmitJ( 02J u2(qw+(1?q)wh;w?wh;)dqds: 

assoziierenkann.MitJ()unddemgestortenFunktional~J()sindjeweilsdualeLosungenwund FunktionG(x;t;x0;t0)zumdualenOperatorvonj(w;x;t)abhangt: ~wverbunden,derenDierenzaufgrundderLinearitatderWellengleichungdurcheineGreensche )=Rj(w;wh;x;t)(x;t)dxdt 

mitj(x;t)=Z1 w=w?~w=ZZT 0G(x;t;x0;t0)j(x0;t0)dx0dt0 

wobeijdurchJ( 0Zs 

zwischendergewunschtenFehleridentitat(2.22)unddergestorten )=Rj( 0@2(j(w)w) ;x;t) @w2 (x;t)dxdtdeniertsei.MitjgiltfurdieAbweichung (qw+(1?q)wh;x;t)dqds(w(x;t)?wh(x;t)); 

EK;n?~EK;n=?(wh;t;w?wh)KIn+(vh;u?uh)KIn 

isteinlinearesFunktionalin 11DieAbleitungeinesFunktionalsF( +(raruh;v?vh)KIn?12([naruh];v?vh)@KIn(2.29) 

vonF derzweitenAbleitungandenPunktenu0undu1;diezweiteAbleitungbeziehtsichdabeiaufdasersteArgument 12IneinigenFallenkannmandasexakteFunktional(2.27)verwenden,selbstwenndiekontinuierlicheLosung u(u0; ). .EbensoistdiezweiteAbleitung2F )aneinerStelleu0wirddurchF u2(u0;u1; u(u0)( )dasinu1und )oderF u(u0; lineareFunktional )bezeichnet;sie 

diskutierenware;daraufseijedochindieserArbeitverzichtet. pathologischeSituationendar,indenendieVerwendungdesFehlerschatzerszurGitterverfeinerunggenauerzu wnichtbekanntist;einBeispieldafuristinAbschnitt5.2gegeben.DieseFallestellenaberingewissemSinne


furallewh.DieAbweichunginderFehleridentitatEK;n?~EK;nhangtdahervomFehlere= 

w?whlinearab,fallsdasZielfunktionalquadratischist,quadratischfallsJkubischist,usw.Sie 

istdamitvoneinerOrdnunghoherimFehleralsdasZielfunktional;wieinAbschnitt3gezeigt 

wird,istderLinearisierungsfehlerabertrotzdemnichtimmervernachlassigbar. 

EineweitereAbschatzungvonEK;n?~EK;nwarehierwunschenswert,istaberschwierig,da 

sowohljalsauchGimallgemeinensingularsindundmannurschwerzuAussagenininteressantenNormenkommt.EinindiesemFallgangbarerWegware,dieNormenuberdieFourier-TransformiertendieserGroenzugewinnen,dadieseindenmeistenFallenmehrRegularitat 

besitzen. 

InderPraxisistnebenderAbschatzungdesFehlers,furdiederhergeleitetelineareZusammenhangmitdemLinearisierungsfehlergilt,wichtig,durchdenFehlerschatzerezienteGitter 

zuerzeugen.DieserProzeistleidernichtlinear,wasdadurchzustandekommt,dadieFehlerindikatorenfurdieeinzelnenZellenderGroenachsortiertunddieZellenindieserReihenfolge 

verfeinertwerden.Dasfuhrtgelegentlichdazu,daZellenverfeinertwerden,dieweitabvondem 

Gebietliegen,dasfurdasZielfunktionalwichtigist,selbstdann,wennderFehlerschatzernur 

maigschlechtdentatsachlichenFehlerbeitragapproximiert.IndiesenFallenistdasGitterfur 

dennachstenDurchlaufnichtbesseralsfurdenaktuellen,sodaderProzeausGitterverfeinerung 

undbessererLinearisierungnichtkonvergiert;dieerzeugtenLosungensindhaugunbrauchbar. 

DieZielfunktionaleimKontextderWellengleichungsindimallgemeinenentwederlinearoder 

quadratischinderLosung;derlineareFallstelltkeineProblemedar,wahrendderquadratische 

FalleinereinfachenVariantederobigenAnalysezuganglichist,dadieIntegraleinderDarstellung 

vonJ()berechenbarsind.WirbetrachtenalsBeispielfalldenEnergieudurcheineKurve: 

J(w)=ZT 

0ZCv(aru)ndsdt: 

Furdiesengiltmitt=('; ): 

2J 

w2(qw+(1?q)wh;w?wh;t)=ZT 

0ZCf (ar(u?uh))+(v?vh)(ar')gndsdt 

unddamitfurdieAbweichungdesFehlerschatzersvomWertbeirichtigerLinearisierung 

J(e)=ZT 

0ZC(v?vh)(ar(u?uh))ndsdt: (2.30) 

DieseGroewirdinAbschnitt3.4.2naherungsweiseausgewertet;dortwirdgezeigt,daineinigen 

praxisrelevantenFallendieLinearisierungsoschlechtseinkann,daderLinearisierungsfehlerJ 

indergleichenGroenordnungwiederWertdesFehlerfunktionalsliegenkann.DashatimallgemeinenzurFolge,daderProzeausGitterverfeinerungundFehlerschatzungnichtkonvergiert, 

dadieGitterverfeinerungkeinegenauereLosungdesprimalenProblemsunddamitauchkeine 

bessereLinearisierungimnachstenVerfeinerungsschrittbewirkt. 

2.4.7BewertungdernumerischendualenLosung 

Unabhangigdavon,obdieFehleridentitatnachdeminAbschnitt2.4.3vorgeschlagenenVerfahren 

oderwieinAbschnitt2.4.4durchAbschatzungmitdemBramble-Hilbert-Lemmaausgewertet 

wird,mudieexaktedualeLosungwdurcheineaufnumerischemWegerhalteneFunktionersetzt 

werden.ImerstenFallwaresnotig,dienumerischedualeLosungmiteinemhoherenAnsatzgrad 

zurechnen,imallgemeinenwurdeerumeinsgroeralsderAnsatzgraddesprimalenProblems 

gewahlt;imzweitenFallisteinbeliebigerAnsatzgradmoglich,meistenswahltmanjedochden 

selbenwiefurdasprimaleProblem. 

DieErsetzungderexaktendurcheinenumerischedualeLosungbewirkteinenzusatzlichen 

FehlerbeiderAuswertungderFehlerschatzer.Wahrendklarist,dadieserFehlervonhoherer 

OrdnungalsdieFehleridentitatist,diewirgeradeauswertenwollen,istdasGroenverhaltnis


x 

t 

x0 

(x1,T) 

x 

t 

x0 

(x1,T) 

x 

t 

x0 

(x1,T) 

Abbildung2.6:DarstellungderProblematikbeiderErsetzungderexaktendualenLosungwdurch 

einenumerischgewonneneLosung.LinksexakteprimaleunddualeLosungen;inderMitteexakte 

duale,abernumerischeprimaleLosung;rechtsnumerischeprimaleunddualeLosung.Weitere 

ErlauterungenimText. 

dieserbeidenWertenichtoensichtlich.ImallgemeinendarfdieErsetzungnichtvolligunkritisch 

durchgefuhrtwerden,wiesichanfolgendemBeispieldemonstrierenlat: 

Wirwollenannehmen,dadieAnfangsbedingungeneineWellegegebenerAusdehnungvon 

x0ausineinevorgegebeneRichtungloslaufenlassen.DerEinfachheithalberbeschrankenwir 

unsaufnureineRaumdimension,sodawirbeikonstantenKoezientendenWegderWelle 

imx?t-DiagrammwieinAbbildung2.6linksmitdurchgezogenenLiniendarstellenkonnen. 

DasZielfunktionalseidiePunktauswertungin(x1;T);dieexaktedualeLosungistdanndurchdie 

avancierteGreenscheFunktiongegeben,derenTragerdasdurchdiegepunktetenLinienbegrenzte 

Gebietist.InhoherenDimensionenistsiejedochnurentlangdergepunktetenLinienvonNull 

verschieden,waswirimfolgendenAnnehmenwollen. 

InderMittederAbbildungistderFalldargestellt,dadieprimaleLosungaufnumerischem 

Wegegerechnetwurde,diedualeLosungabernachwievorexaktbekanntist.Aufgrunddesin 

Abschnitt4.5.2geschildertenProblemsistdienumerischeAusbreitungsgeschwindigkeithoherals 

dieexakte;dieSteigungderBegrenzungsliniendesTragersderprimalenLosungistdahergroer 

alsimexaktenFall.Verfeinerungwirdnundortstattnden,wosichdieTragervonnumerischer 

primalerundexakterdualerLosunguberlappen,d.h.imschattiertenBereich.DieVerfeinerung 

wirddazufuhren,daderlinkeTeilderWelleimnachstenDurchlaufnaheranderexaktenLosung 

ist,alsoinsbesonderedadieAbweichungderAusbreitungsgeschwindigkeitgeringerist.Derrechte 

TeilwirdnichtverfeinertundbehaltdamitseinefalscheGeschwindigkeit,wasallerdingsauchnicht 

schlimmist,daerohnehinnichtzumZielfunktionalbeitragt. 

Esistoensichtlich,dabereitsindiesemFallmitexakterdualerLosungdieKonvergenzgegendierichtigeprimaleLosungrechtlangsamgehenkann,danuretwaindererstenHalftedes 

Zeitintervalls(0;T)uberhauptVerfeinerungauftritt.ImbestenFallistdienumerischeLosung 

dortexakt,furgroereZeitenjedochistdieAusbreitungsgeschwindigkeitimnachstenDurchlauf 

ebensofalschwieimerstenundmanbrauchtmehrereSchritte,bisuberhaupterstdasganze 

Zeitintervallverfeinertist.JegroerdieAbweichungzwischenexakterundnumerischerAusbreitungsgeschwindigkeitist,destomehrSchrittesindnotig,umdenganzenWegzwischenUrsprungsundAuswertungspunktzuverfeinern. 

DasProblemverschlimmertsichnoch,wennauchdiedualeLosungnumerischgewonnenwerdenmu(rechterTeilderAbbildung):dannistauchdieAusbreitungsgeschwindigkeitderdualen 

LosungfalschunddieTragerderbeidenFunktionenuberlappenuberhauptnichtmehrinBereichen,diefurdasZielfunktionalrelevantsind.IndiesemFallwirdderFehlerschatzereinenWert 

NullzuruckgebenundalleZellenzuZeitenvergrobern,dievorderZeitliegen,wosichderrechte 

TeilderdualenLosungunddieprimaleLosunguberschneiden.EskannhierkeineKonvergenz 

gegendierichtigeLosunggeben. 

AufgrunddergeschildertenProblematikistesnotwendig,dieVerfeinerungmitdemdualen 

Fehlerschatzererstdannzubeginnen,wennschonguteNaherungenfurdieprimaleLosungvor-

handensindundwenndasGittergutgenugzurBerechnungderdualenLosungist.InderPraxis zeigtessich,daesfurletzteresnichtausreicht,diedualeLosungaufderSchnittmengederTrager 30 KAPITEL2.NUMERIKDERWELLENGLEICHUNG 

derbeidenLosungengutzuapproximieren,sonderndaesnotigist,dasGitterauchgeeignetan diedualeLosunganzupassen(vgl.Abschnitt4.5.1). lerschatzungnichtmoglichist.DieberechnetenFehlerschatzerzeigenimallgemeineneinenur schwacheKorrelationmitdemtatsachlichenFehlerundliegenoftumeinbiszweiGroenordnungendaneben;allerdingssinddieerzeugtenGittersehreektiv,wasdenverwendetenAnsatz 

rechtfertigt.DieschlechteApproximationdesechtenFehlersdurchdenFehlerschatzeristnaturlich Danebenzeigtsichallerdingsauch,dainpraxisnahenBeispielenquantitativrichtigeFeh- 

AuswirkungderErsetzungw!w(r+1) instabileAuswertungderFehleridentitat,beidereinIntegraluberzweistarkoszillierendeFunktionen,namentlichdasResiduumund(1?Ih)w,ausgefuhrtwerdenmu.DieGenauigkeitdes 

SchatzerskannunterUmstandenverbessertwerden,wennbeiseinerBerechnungdieGalerkin- Orthogonalitatnichtausgenutztwird,sodadieIntegralenuruberdasoszillierendeResiduum, h undwirdverstarktdurchdiegegenuberkleinenStorungen 

teriumshatallerdingsausdengeschildertenGrundenunterVerwendungeinerInterpolationund aberubereineglatteFunktionwausgefuhrtwerdenkonnen;dieBerechnungdesVerfeinerungskri- 

derGalerkin-Orthogonalitatzugeschehen.

Kapitel3 

Anwendungaufdiesolare Atmosphare 

DickebeiderSonnerund2.200kmbetragt.IndieserbewegtsichdieTemperaturzwischen4.000 DieimvorigenKapitelhergeleitetennumerischenMethodensollenindiesemAbschnittaufein ache(Photosphare)dermeistenSternbendetsicheineChromospharegenannteSchicht,deren und20.000K.NachauenhindirektanschlieendsteigtdieTemperaturineinerkleinenUbergangszonevon100-200kmDickeaufmehrereMillionenKelvinanundauchdieDichteandertsich 

DimensionenverglichenmitderDickederChromosphareweitgehendkonstant. WegenderkaltenSchichtzwischenSonneninneremundKoronakommenwederWarmeleitungnoch starkenMagnetfeldernundmagnetohydrodynamischenEektenausHeizungdurchSchockwellen. terEnergieuvorhandensein.DertatsachlicheHeizungsmechanismusbestehtvermutlichneben StrahlungsheizunginFrage;andererseitskannauchausdeminterstellarenRaumkeinnennenswer- 

EinephysikalischnurteilweiseverstandeneFrageistderMechanismusderHeizungderKorona. 

BeispielausderPhysikstellarerAtmospharenangewendetwerden.OberhalbdersichtbarenOberummehrereGrosenordnungen.Indieser,Koronagenannten,SchichtbleibtdieTemperaturauf 

AkustischeWellenwerdendabeiaufderSonnenoberachedurchdiedortvorhandenenKonvektionsstromungenerzeugtundbewegensichinderChromosphareundderanschlieendenKorona 

nachauen;inderdunnenGasatmospharebildensieschnellstarkeSchocks,dieinderLagesind, 

durchgefuhrt,allerdingszueinemgroenTeilmitnureinerRaumdimension(vgl.[33,25,31,32]) Energiezudissipieren. isteswichtigsienumerischzusimulieren.SolcheSimulationenwerdenseitvielenJahrenerfolgreich eineRaumdimensionwirdgemeinhinalswunschenswertbezeichnet,umrealistischeModellezur undnurinwenigenArbeiteninzweiDimensionen(z.B.[26]).DieErweiterungaufmehrals UmdenEnergieeintragindieChromospharedurchakustischeWellenabschatzenzukonnen, 

AusbreitungakustischerWellenindersolarenAtmosphareverwendenzukonnen. nichtmoglichsind,lassensichdiesenurdurchdieLosungeinesinversenProblemsgewinnen;dazu schenGroenTemperaturundDichtehinreichendgenaubekanntsind.DadirekteMessungen werdenMessergebnissemitSimulationsergebnissenfureingegebenesModellverglichen,umdas Modellzuverbessern.SolcheRechnungensindauerordentlichaufwendig,dadiezuberucksichtigendenphysikalischenEektesehrvielfaltigsindundnebendenGasgleichungenauchStrahlungfekteaufgrundderHeizungdurchSchockwellenbeinhalten.DieInversionderMedatengeschieht 

imallgemeinendurchtrialanderrorundzusatzlichephysikalischeAnnahmen.UmfangreicheDarstellungzudiesemProblemsindbeispielsweisein[34,15,10]zunden.ImRahmendieserArbeit 

wurdeeinModellfurDichteundTemperaturaus[32]verwendet(bKmG{broadenedKolmogorov, modiedGauss),beidemdynamischeEekteaufgrundakustischerWellenmitberucksichtigtwurden;dasFrequenzspektrumderdasMediumheizendenWellenfolgtdabeieinerVerteilung,dieaus 

DieSimulationvonPhanomeneninderSonnenatmospharesetztvoraus,dadiephysikali- 

NichtgleichgewichtseektedurchdengerichtetenEnergieudurchStrahlungunddynamischeEf- 

31

14000 

12000 

32 TurbulenzmodellenundAnpassungenandiesolareUmgebunghergeleitetwerdenkann(vgl.[31, Abschnitt2.2]). KAPITEL3.ANWENDUNGAUFDIESOLAREATMOSPHARE 

dargestellt.ManerkenntdeutlichdenBeginndessteilenAnstiegsanderGrenzezwischenChromosphareundKorona.DieTemperaturschwanktinderKoronazwischenetwa2undbiszu6 

MillionenKelvin;furdieRechnungenwurdeeinAnstieginnerhalbvon200kmaufeinekonstante Temperaturvon2MillionenKelvinangenommen,wobeidaraufhingewiesensei,dadieseTemperaturwahldasErgebnisderRechnungenwesentlichzubeeinussenvermag.Ausdengegebenen 

DatenfurTemperaturTundDichtelatsichderKoezienta(x)inderGleichung(1.1)nach folgendenFormelnherleiten: c2=RT a=c2: ; 

DerausdiesemModellhergeleiteteVerlaufderTemperaturistinAbbildung3.1beispielhaft 

hohenDichtezu53gewahltwerdenkann,RdieallgemeineGaskonstanteund=1:3dasmittlere DabeiistcdielokaleAusbreitungsgeschwindigkeit,derAdiabatenkoezient,deraufgrundder MolgewichtdesGases. 

10000 

8000 

Abbildung3.1:VerlaufderTemperaturimbKmG-Modell(aus[32]).Nachobenhinsteigtdie 

6000 

TemperaturaufzweiMillionenKelvin;dieserAnstiegistnichtmehrdargestellt,umdieTemperaturvariationeninderChromospharenochdarstellenzukonnen. 

4000 

2000 

’bKmG’-Modell 

0 

0 500 1000 1500 2000 2500 

NebendemerwahntenModellaus[32]wurdenauchRechnungenmitanderenTemperaturmodellendurchgefuhrt,beispielsweiseModellCaus[34]undmitdenErgebnissenaus[15]und[10]. 

WellenpraktischnurdurchReexionanderUbergangsschichtzwischenChromosphareundKoronabehindertwird,wahrenddieTemperaturvariationeninderChromospharepraktischkeinen 

DieErgebnissestimmtenmiteinanderimRahmenderGenauigkeitderRechnungenweitestgehend 

Hoehe [km] 

beiallenModellenimwesentlichengleich. Einuhaben,imGegensatzzumFallnichtlinearerWellen;derTemoeraturanstiegverlauftaber uberein.Dasistdaraufzuruckzufuhren,daderEnergieuindieKoronabeilinearenakustischen 

Situationangenommen,indemeineReduktionaufnurzweiRaumdimensionenundvorallemeine VernachlassigungallernichtlinearerEekteindenGasgleichungendurchgefuhrtwird.AuchwurdenwederStrahlungstransportnochthermischeNichtgleichgewichtsbedingungenverwendet.Die 

erhaltenenErgebnissesinddahernursehrbedingtmitMessungenunddenErgebnissennichtlinearerBerechnungenvergleichbar;dasZieldieserArbeitisteherdieDemonstrationdergenerellen 

WieschoninderEinleitungzudieserArbeiterlautert,wirdeinestarkeIdealisierungdieser 

OrdnunginderZeit. AnwendbarkeitadaptiverMethodenaufWellenphanomeneundhyperbolischeGleichungenzweiter 

Temperatur [K]

u=0 

60.000 km 0 km 18.000 km 0 km 

4.000 km 

du/dn=0 

u=0 

3.000 km 

2.450 km 

2.250 km 

3.1.DEFINITIONDESGEBIETSUNDDERRANDBEDINGUNGEN schlieenddieverschiedenenMoglichkeitenderAuswertungderRechnungendiskutiert.Schlielich IndenfolgendenAbschnittenwerdenzuerstdieDenitiondeszurechnendenTestfallsundan- 

33 

3.1 werdendieErgebnissederRechnungenprasentiert. 

RechengebietundRandbedingungenwerdenimwesentlichendurchdiephysikalischeProblemstellungbestimmtundsindinAbbildung3.2dargestellt.AlsRandwertfunktionfurdenunterenRand 

wurdeDenitiondesGebietsundderRandbedingungen 

gewahlt;dadurchlauftvonderlinkenunterenEckeeineWelleindasGebiethinein.IndenRechnungenwara=50km,dasheitimVergleichzumgesamtenGebietsehrklein;wurdezu60 

gD(x;0;t)=cos?2xasin?tfurx

34 KAPITEL3.ANWENDUNGAUFDIESOLAREATMOSPHARE 

DarstellungindierentiellerForm:gemadem"klassischen\Ansatzaus[14]lassensichdie 

exaktenRandbedingungenalsinderZeitundimOrtnichtlokalenIntegraloperatorschreiben. 

DieserkannalsPseudodierentialoperatoraufgefatundineineTaylor-Reiheentwickelt 

werden,waseineHierarchievonzunehmendgenauerenRandbedingungenergibt.Dieersten 

GliederdieserFolgesindimfolgendenfurzweiRaumdimensionenundtrivialeKoezienten 

(a==1)angegeben(tbezeichneeinenTangentenvektoranderRand): 

@u 

@n+v=0; 

@v 

@n+@v 

@t?12@2u 

@t2=0; 

@2v 

@n@t+@2v 

@t2?14@3u 

@t2@n?34@2v 

@t2=0: 

DieRandbedingungensindjeweilsfursenkrechtauftreendeWellenidealabsorbierend, 

wahrenddieAbsorptionmitderAbweichungdesAuftrewinkelsvonderSenkrechtenimmerschlechterwird(esistbekannt,vgl.[20],dalokaledierentielleRandbedingungendiese 

EigenschaftinharentinsichtragenundnichtfuralleEinfallswinkelundFrequenzenideal 

absorbierendseinkonnen).DadieQualitatdererstenApproximationnichtsehrgutist,die 

ImplementationsowiediemathematischeFormulierungineinemFiniten-Elemente-Ansatz 

mitpolynomialenAnsatzfunktionenbeidenfolgendenGliedernwegenderschnellhoher 

werdendenAbleitungenaberschwierigist,wurdeaufeineVerwendungverzichtet. 

ExakteRandbedingungenInjungererZeitwurdenexakteabsorbierendeRandbedingungen 

furakustische,elastischeundelektromagnetischeWellengleichungenvorgeschlagen(vgl.[18, 

17]),dieinderZeitlokalsindundnurersteAbleitungenenthalten.SiesindjedochnichtlokalimOrt(esisteineEntwicklungderLosungnachKugelfunktionendurchzufuhren)und 

ihrgroterNachteilbestehtdarin,dasienuraufderOberacheeinerKugelgelten;eine 

VerallgemeinerungaufbeliebigeGebieteerscheintauerindenFallenausgeschlossen,wodie 

EigenfunktionendesLaplace-OperatorsaufdemRanddesGebietsbekanntsind. 

"NichtreektierendeRandbedingungen\:unterdiesemNamenwirdinderIngenieursliteratur 

(vgl.zumBeispiel[11])dieTechnikgefuhrt,umdasGebietherumeineodermehrereSchichtenvonZellenzulegen,indenenderGleichungeinDampfungstermhinzugefugtwird.In 

diesemBereichwirdjedeeinlaufendeWelleexponentiellgedampft.UmeineguteAbsorption 

zuerreichenistjedocheinemitkleinerwerdenderWellenlangegroereSchichtvonZellen 

notwendig;daruberhinausistdieDampfungzwarexponentiell,jedochnichtvollstandig,so 

daeinkleinerTeilderWelletrotzdemreektiertwird. 

AlledreivorgeschlagenenVerfahrenforderneineUmformulierungdesursprunglichenProblems 

sowieerheblichenImplementationsaufwand.EswurdeinUbereinstimmungmitderFragestellung 

diefolgendenLosungverfolgt:dareektierteWellennurdanneinProblemdarstellen,wennsie 

EnergieuberdieAuswertungsliniein3000kmHohetransportieren,istlediglichReexionamoberenRandproblematisch.ReexionamrechtenRandunterhalbderUbergangszoneisterwunscht, 

dasiedasGebietvirtuellnachrechtsfortsetztundsomitselbstdieWellenspateraufdieUbergangszonetreen,derenWeganfangszuachverliefumnochvordemrechtenRandbisineine 

Hohevon2250kmzugelangen.OberhalbderUbergangszoneistdieReexionvomrechtenRand 

nichtrelevant,dadieWellenvonuntenkommenundsomitauchwiederschragnachobenreektiert 

werden,sodakeinEnergieuuberdieAuswertungsliniezuruckzubefurchtenist.Ausdiesen 

beidenGrundenwurdenrechtsreektierendeRandbedingungengesetzt;dieWahlvonDirichletgegenuberNeumann-Wertenisthierbeiwillkurlich. 

UmdiealleinunerwunschteReexionvomoberenRandzuverhindern,wurdedieserdurch 

PlazierungeinigernachobenhingroerwerdenderZellenweitnachobenverlagert;derAbstand 

vomunterenRandwurdedabeisogewahlt,dadieWelleninnerhalbderSimulationszeitdas 

Gebietnichtvonuntennachobenundzuruckdurchwandernkonnen.DaderAbstandaufgrund

derimoberenBereichsehrhohenAusbreitungsgeschwindigkeitrechtgroseinmute,wurdeeine ModikationdernichtreektierendenRandbedingungenverwendet.DazuwirddieAusbreitungsgeschwindigkeitnachobenhin,vondertatsachlichenPhysikabweichend,verringert;ndetdiese 

VerringerungaufeinerLangenskalastatt,diegrogegenubertypischenWellenlangenist,soist keineReexionvonWellenzuerwarten,diesewerdenlediglichabgebremst.Auchbeeinutdiese ModikationdieimGebietvorhandeneEnergienicht,wasdieAuswertungderEnergieussever- 

ProblemsymmetrischistundsomitnurdieHalftederWellegerechnetwerdenmu.Umnach zuverwenden;dieWahlvonDirichlet-Bedingungenistwiederwillkurlich. einfacht.InderSummeerlaubtdieserAnsatz,amoberenRandreektierendeRandbedingungen obenhingroerwerdendeZellenverwendenzukonnenohnedabeiderenSeitenverhaltniszuverschlechtern,wurdeeinnachobenhinbreiterwerdendesGebietverwendet.DadieAusdehnungdes 

GebietskleingegenuberdemDurchmesserderSonneist,istesnichtnotig,dieWellengleichungin AlsRandbedingungfurdenlinkenRandwurdenhomogeneNeumann-Wertegesetzt,dadas 

3.2.AUSWERTUNGDERRECHNUNGEN 35 

Zylinder-stattkartesischenKoordinatenzulosen. 3.2 ZielderRechnungenwares,denAnteilderEnergieeinerWellezubestimmen,derdieGrenzschicht passierenkann.DazugibtesimwesentlichendreiMoglichkeiten: AuswertungderRechnungen 

DirekteAuswertungdesEnergieusses:daderEnergiestromdurch 

tegrationerhalten: gegebenist,latsichdiegesamte,durcheineKurveCieendeEnergiemengedurchAun- 

j=varu 

EnergiemengeoberhalbderAuswertungslinie:daursprunglichkeineEnergieimGebietwar J(w)=ZT 

undaufgrunddergewahltenRandbedingungenauchkeinEnergieverlustdurchdenRand 0ZCv(x;t)(a(x)ru(x;t))ndsdt: 

gleichderdurchdieLiniehindurchgetreteneEnergiesein: moglichist,mudiezumEndzeitpunktoberhalbderAuswertungslinievorhandeneEnergie 

numerischenStorungenunterlegen.DiestritwegenderimoberenTeildesGebietssehr WieinAbschnitt2.1.3beschrieben,istdieEnergiebeiVerwendungveranderlicherGitter J(w)=Ey>y0(T)=Z\fy>y0g12(x)v(x;T)2+12a(x)(ru(x;T))2ddx: 

groenZellenbeiderAuswertungdiesesFunktionalsbesonderszu;Abbildung3.3zeigt beispielhaftdenVerlaufderEnergieoberhalbderAuswertungslinie.DawegenderStufen demZeitverlaufbestimmt,indemdasMaximumdesVerlaufsgenommenwurde;eswurde derWertderEnergieamEndzeitpunktnichtsehrzuverlassigist,wurdeJ(w)mitHandaus Schatzungzuerhalten.ZumindestfurdiefeinerenGittergibtesimallgemeinennurnoch einenoderzweiklarerkennbareSprungeineinemBereich,wodieKurveschonsehrach nichtversucht,denweiterenVerlaufohnedieSprungezuantizipierenundsoeine"bessere\ 

EnergiedierenzunterhalbderAuswertungslinie:ebensomuderEnergieudurchdieLinie ist,sodadieAuswertungmitHandrechtzuverlassigerscheint. gleichderDierenzderEnergiensein,dienachEinbringungderWelleundzumEndzeitpunkt imunterenTeilgebietvorhandensind: J(w)=E(t=)?Ey

36DieseAuswertungistimallgemeinensehrvielschlechter,dadieEnergiedierenznurwenige 

ProzentederGesamtenergiemengeausmachtunddahersehrvielanfalligeristgegenuber KAPITEL3.ANWENDUNGAUFDIESOLAREATMOSPHARE 

werdendannirrtumlichdemErgebnisdieserAuswertungzugerechnet.ErstbeiRechnungen mitextremvielenFreiheitsgradenkommtdernumerischeEnergieverlustbeiRechnungen numerischenStorungenderGesamtenergie.TypischerweisegehenindenerstenVerfeinerungsschrittenmehrerezehnProzentderEnergiedurchnumerischeProblemeverloren;diese 

jedochimmernocherheblichistgegenuberdenWertendiesesFunktionals. mitstarkschwankendenKoezientenindieGroenordnungvonuntereinemProzent,was 

dieseAbnahmemuaufnumerischeEektezuruckzufuhrensein.DieGultigkeitdieserKor- 

wennmandieAbnahmederGesamtenergiezwischent=undt=TvonJ(w)abzieht; DieAuswertunglatsichjedochnaherungsweiseumdenbeschriebenenFehlerkorrigieren, 

ist,istdieseAnnahmerechtguterfullt,sodawir bietsstattndet;dadortderbeiweitemuberwiegendeTeilderGesamtenergiekonzentriert rektursetztvoraus,dadernumerischeVerlustausschlielichimunterenTeildesRechenge- 

alsAuswertegroeansehenkonnen. J(w)=(E(t=)?Ey

3.3.ADAPTIVITAT Adaptivitat 37 

BeiderDurchfuhrungderRechnungenzeigtesich,daohnedieVerwendungadaptiverGitter keineverwertbarenErgebnisseerzeugtwerdenkonnten,dadiedazunotigeAnzahlanGitterzellen wesentlichgroerwar,alsesRechenzeit-undSpeicherbeschrankungenerlaubten.SelbstdieadaptivenRechnungenbenotigtenmehrereZehnmillionenFreiheitsgrade,1umErgebnissezuliefern, 

der"traditionelle\Fehlerindikator(2.9),imfolgendenkurz"Energiefehlerindikator\genannt,2 derenrelativeGenauigkeitbeivielleicht2oder3Prozentliegt. andererseitsderimletztenKapitelvorgestellteFehlerschatzeraufderBasisdesdualenProblems Verwendungfand.FurdieRechnungenmitdemdualenProblemwurdendiefolgendenFehlerfunktionalegewahlt,diedendreiAuswertungsmoglichkeitenobenentsprechen;daalledreiFunktionale 

EswurdenvergleichendeRechnungendurchgefuhrt,wobeialsVerfeinerungskriterieneinerseits 

nichtlinearsind,mudieinAbschnitt2.4.1erlauterteLinearisierungverwendetwerden: DirekteAuswertungdesEnergieusses: 

EnergiemengeoberhalbderAuswertungslinie: ~Jw(t)=ZT 0Z(v(x;y0;t)(ar')n+ (aru(x;y0;t))n)dx: 

EnergiedierenzunterhalbderAuswertungslinie: ~Jw(t)=(v(;T); (;T))\fy>y0g+(aru(;T);r'(;T))\fy>y0g: 

~Jw(t)=h(v(;); ?h(v(;T); (;))\fy

Energiefluss in willkuerlichen Einheiten 

3e+07 

2.5e+07 

4 Verfeinerungen, 934.488 Freiheitsgrade 

38 derProzeausadaptiverGitterverfeinerungundRechnungnicht,obwohldieZellzahlbestandig zunimmt. KAPITEL3.ANWENDUNGAUFDIESOLAREATMOSPHARE 

auchdieextremschlechteKonvergenzdiesesFunktionalsaufnichtausreichendfeinenGittern beiderAuswertungdesLinienintegralsalsdualemFunktionalangefuhrt.DasBeispielzeigtdabei (wenigeralsca.5000FreiheitsgradenimMittelproZeitschritt). UmdieKonvergenzproblemeweitentferntvomKonvergenzpunktzuillustrieren,seieinBeispiel 

Verfeinerungsschritten(mitdemEnergiefehlerschatzer)dargestellt.LegtmandenVerlaufnach achtVerfeinerungsschrittenzugrunde,sowirddiedualeLosungimwesentlichenausdreiPulsen bestehen,dievonderLiniezudenZeiten345s,370sund400sausgehenundinderZeitzuruckpropagieren;dasGitterwirdnurentlangdesWegesdieserdreiPulseverfeinertwerden.Fingeman 

InAbbildung3.4istderEnergieudurchdieAuswertungslinienachvierundnachacht 

dualeLosungnebendenbeidenmarkantenPulseneinenstarkenAnteil,derausdemRauschen jedochbereitsnachvierVerfeinerungsschrittenmitdemdualenFehlerschatzeran,sobesaedie stammt,dasabetwa400seinsetzt.DadiesesRauscheninderRuckwartsrechnungvordenbeiden PulsenvonderLinieausgeht,istdasGebietwodiedualeLosungmerklichvonNullverschieden ist,erheblichgroeralsnotwendig,wasdiefureinegegebeneGenauigkeiterforderlicheZellzahl wesentlichindieHohetreibt.HierkommtdaruberhinauszumTragen,dadiedualeLosungnach t450spraktischgleichNullist,sodamandieweitereRechnungaufeingrobesGitterundgroe Zeitschrittebeschrankenkann,dadieFehlerindikatorennaheNullsind,wasbeiLinearisierungum denlinksgezeigtenEnergieuunerkanntbliebe.3 

2e+07 

2e+07 

1.5e+07 

1.5e+07 

Abbildung3.4:EnergieudurchdieAuswertungslinieinAbhangigkeitvonderZeitbeiverschiedenenVerfeinerungsstufen.DieVerfeinerunggeschahdurchdenEnergiefehlerindikator. 

1e+07 

1e+07 

5e+06 

5e+06 

0 

0 

-5e+06 

-5e+06 

0 100 200 300 400 500 600 700 

0 100 200 300 400 500 600 700 

3.4 [s] 

[s] 

wiebeiVerfeinerungmitdemEnergiefehlerindikatorunddemdualenFehlerschatzergegenuber- 

gestellt.Eszeigtsich,dagenaueWertefurdieinteressierendeGroe,denAnteildervonder ist0:02700:0015,d.h.eswerdenknappdreiProzentderEnergiedurchgelassen.DieserWert liegtineinerGroenordnung,diemiteinereinfachenRechnungauchzuerwartenist:deranaly- 

UbergangsschichttransmittiertenEnergie,nurmitdenRechnungenzuerhaltenwaren,beidenen dasGittermitdemEnergiefehlerindikatorverfeinertwurde;dervermutlicheWertfurdieseGroe IndenfolgendenAbschnittensinddieErgebnissederRechnungenbeiglobalerVerfeinerung,so- 

Zeitschrittenangehoren.Diesistbeibiszu50.000.000FreiheitsgradeneineerheblicheprogrammtechnischeHerausforderung.ImverwendetenProgrammwurdedieseOptimierungdeshalbnichtverwendet,obwohlklarist,dasitischeAusdruckfurdenaneinerUnstetigkeitdesBrechungsindex'transmittiertenEnergieanteils 

derdieFehlerindikatorenzweierRaum-Zeit-Zellenauchdannmiteinanderverglichenwerden,wennsieverschiedenen zueinerweiterendrastischenReduktionderFreiheitsgradefuhrenwurde.ZuDetailshierzuvergleicheAbschnitt 3DieVerwendungdieserInformationsetztvoraus,dadieGitterverfeinerungineinerArtdurchgefuhrtwird,bei 4.5.3. 


3e+07 

2.5e+07 

8 Verfeinerungen, 42.026.038 Freiheitsgrade

istdurch 3.4.ERGEBNISSEDERRECHNUNGEN E E=n n0+n=1 39 

zu sindn;n0linearvonderWurzelausderTemperaturTabhangig,sodasichderEnergiebruchteil gegeben,wobein0undndieBrechnungsindizesaufdenbeidenSeitenderUnstetigkeitsind.Hier n+1 

ergibt.BerucksichtigtmannochdenstreifendenEinfalleinesTeilsderWelle,soistdererhaltene E EqTKorona 

TChromosphare+11 1 

WertinderGroenordnungdeserwarteten. 20+10:048 

3.4.1VerfeinerungmiteinemEnergiefehlerindikator IndenAbbildungen3.5und3.6sinddieErgebnissederRechnungenbeiVerfeinerungmitdem Energiefehlerindikatordargestellt.DasGitter4istrechtgutandieLosungangepat,esfolgtsowohl dertransmittiertenWellemitihrerhohenGeschwindigkeit,alsauchdemnachuntenzuruckreektiertenAnteil. 

Abbildung3.5:MitdemEnergiefehlerindikatorerzeugteGitterzudenZeitent=250s,375sund 

folgendenzusammenfassen: 650s. 

DieAuswertungderEnergieoberhalbderMeliniekonvergiertrechtgutgegeneinenfesten DieErgebnissendernumerischenAuswertungderRechnungeninAbbildung3.6lassensichdie Wert.DagegenistdieAuswertungderEnergiedierenzunterhalbdieserLiniesehrungenau; 

ErsatzfurabsorbierendeRandbedingungeneingefuhrt,sodadortnichtswesentlichesmehrpassiert. 4EsistnurderuntereTeildesGebietsdargestellt,danurdieserinteressantist.DerobereTeilwurdenurals dasliegtdaran,dadernumerischeVerlustinderGesamtenergie,derdurchdievariablen Gitterverursachtwird,diesemFunktionalzugerechnetwird.DasichdieindenoberenTeil


Energieanteil, der die Uebergangszone passiert 

0.06 

0.05 

Linienintegral 

Energiedifferenz in der unteren Atmosphaere 

Energie in der hohen Atmosphaere 

0.04 

0.04 

0.03 

0.03 

Abbildung3.6:ErgebnissederverschiedenenAuswertungsmethodenbeiRechnungenmitdemEnergiefehlerindikator;linksbilineareElemente,rechtsbikubische.AufgetragenistderdieUbergangsschichtpassierendenAnteilderGesamtenergiegegendiekumulierteAnzahlanFreiheitsgraden. 

0.02 

0.02 

0.01 

0.01 

0 

0 

10000 100000 1e+06 1e+07 1e+08 

10000 100000 1e+06 1e+07 1e+08 

desGebietstransmittierteEnergiemengenurinderGroenordnungvonzweibisdreiProzent 

derGesamtenergiebewegt,muletzterenumerischaufwesentlichbesseralseinProzent konstantgehaltenwerden.DiesisterstindenletztenVerfeinerungsschrittenderFall,soda davoristdasGitternochzugrob. ArtvonStorungen,daaufdereinenSeiteohnehinnurnumerischerEnergieverlustnach erstindieseneineguteGenauigkeitbeiderAuswertungdiesesFunktionalsgegebenwar; AndererseitsistdieAuswertungderEnergieoberhalbderMeliniesehrstabilgegendiese t=eineRollespielt,aufderanderenSeitederEnergieverlustimHauptteilderWelle, d.h.unterhalbderLinieirrelevantist.BewegtsichdernumerischeEnergieverlustalsoin verfalschterauchdasErgebnisbeidiesemFunktionalnurumdieentsprechendeAnzahlan Prozenten,wahrenderbeiderAuswertungderEnergieunterhalbderLinieeinenFehlervon derGroenordnungvonbeispielsweiseeinigenProzentaufeinemmaigfeinenGitter,so 

DieAuswertungmitdemLinienintegralkonvergiertebenfallsrechtschlecht.Diesistverstandlich,beachtetmandieVerlaufeinAbbildung3.4unddecktsichmitdergenerellen 

mehrerenhundertProzentausmachenkann. Aussage,dadieKonvergenzordnungvonIntegralenuberLinienoderPunktauswertungen hinwegtransportiertwird,wasletztlichmitderHerleitungdiesesIntegralsalsDivergenz derEnergiemengeineinemderbeidenTeilgebietezusammenhangt;derCharakterdieses daessichnichteigentlichumeinLinienintegralhandelt,dadieEnergiejauberdieLinie eineschlechtereKonvergenzordnunghabenalsGebietsintegrale.Andererseitsistzubeachten, 

AusdemrechtenTeilderAbbildung3.6latsichdiedeutlichbessereKonvergenzderRechnungmitbikubischenElementenablesen.VorallemdieErhaltungderGesamtenergieist 

beielliptischenGleichungen. FunktionalsentsprichtdahereherdemeinesGebietsintegralsalsdemeinesLinienintegrals 

erheblichbesser,sodadieAuswertungderEnergiedierenzunterhalbderAuswertungslinienbessereErgebnissezeigt.DieAuswertungdesLinienintegralsistjedochebensounsicher 

wiebeilinearenElementen.TrotzderniedrigerenAnzahlvonFreiheitsgradenfureinevergleichbareGenauigkeitistdernumerischeAufwandnichtgeringerodersogarhoheralsbei 

linearenElementen,dadieAnzahlderEintrageindemSystemmatrizengroerist,wasdie 

Wert0:02700:0015,dasheitmiteinerGenauigkeitvonrundfunfProzentbestimmen.Die derAuswertunglatsichfurdenAnteildervonderUbergangszonetransmittiertenEnergieder AusdenjeweilsgenauestenErfgebnissenderbeidenRechnungenunddenverschiedenenWegen benotigteAnzahlanOperationenfurMatrix-Vektor-Multiplikationenerhoht. 


0.06 

0.05 



Energie in der hohen Atmosphaere

Intervallsliegen. Fehlergrenzenwurdendabeisymmetrischsogewahlt,daallesechsDatenpunkteinnerhalbdieses 3.4.ERGEBNISSEDERRECHNUNGEN 41 

3.4.2VerfeinerungmitdemdualenSchatzer IndenAbbildungen3.7,3.8und3.9sinddiemitdendreinichtlinearenZielfunktionalenerzeugten Gitterdargestellt.DieGitter,diemitdemlinearenZielfunktional(3.1)erzieltwurden,ahneln denendesnichtlinearenFunktionalsaufderAuswertungslinie,sindaberetwasvoller.ImwesentlichenentsprechendieGitterdem,wasmanaufgrundderanschaulichenBedeutungdesdualen 

Problemsjeweilserwartenwurde.Esistdabeizubeachten,dazuerstetlicheVerfeinerungsschritte mitdemEnergiefehlerindikatordurchgefuhrtwurden,bevoraufdendualenSchatzerumgeschaltet wurde;danureinigewenigeSchrittemitletzteremgemachtwurden,bestehennochBereichemit relativfeinenZellen,dienichtzumZielfunktionalbeitragen,beispielsweiseober-undunterhalb zeitpunktinAbbildung3.8undoberhalbjenerinAbbildung3.9.DieseBereichewurdeninden derAuswertungslinieamEndzeitpunktinAbbildung3.7,unterhalbderAuswertungslinieamEnd- 

nachstenVerfeinerungsschrittenaufgelostunddurchgrobeGitterersetzt,wofurallerdingsmehr VerfeinerungsschrittemitdemdualenFehlerschatzernotigwaren. 

Abbildung3.7:MitdemdualenSchatzererzeugteGitterzudenZeitent=250s,375sund650s. AlsFehlerfunktionaldientederFludurchdieAuswertungslinie. AuswertungenderRechnungenenttauschendesVerhalten.DiesesistindenAbbildungen3.10und dreiWegederAuswertungdargestellt;allerdingsisteigentlichnurdiezumZielfunktionalpassende 3.11furdievierverschiedenenZielfunktionaledokumentiert.InjederderAbbildungensindalle angebracht,dieinAbbildung3.12furdieverschiedenenRechnungeneinandergegenubergestellt WahrenddieGitterinetwadenerwartetenentsprechen,zeigendienumerischenErgebnisseder 

indenAbbildungenvermerkt.NachdemaufdendualenFehlerschatzerumgestelltwurde,verringertsichdieZellzahlhaugindenerstenSchritten,damehrZellenaufgelostalsverfeinertwerden, 

sodadieKurvenrucklaugesVerhaltenzeigen.ErstnacheinigenwenigenVerfeinerungsschritten BeidengezeigtenKurvenistzubeachten,dadieerstenDatenpunktejeweilsdurchVerfeine- 

werden. rungmitdemEnergiefehlerindikatorerhaltenwurden.DieentsprechendeAnzahlanSchrittenist mitdemdualenFehlerschatzernimmtdieAnzahlderZellenwiederzu.


Abbildung3.8:MitdemdualenSchatzererzeugteGitterzudenZeitent=250s,375sund650s. AlsFehlerfunktionaldientedieEnergieoberhalbderAuswertungsliniezumEndzeitpunkt. 

Abbildung3.9:MitdemdualenSchatzererzeugteGitterzudenZeitent=250s,375sund650s. AlsFehlerfunktionaldientedieDierenzderEnergienunterhalbderAuswertungsliniezuden Zeitpunktent=T=650sundt==60s.

3.4.ERGEBNISSEDERRECHNUNGEN 43 


0.06 

0.05 




0.04 

0.04 

Abbildung3.10:ErgebnisderAuswertungenbeiVerfeinerungmitdemdualenProblem.Links 

0.03 

0.03 

Verfeinerungmitdemnichtlinearen,rechtsmitdemlinearenLinienintegral,wobeidieersten7 

0.02 

0.02 

bzw.5DatenpunktemitdemEnergiefehlerindikatorgewonnenwurden. 

0.01 

0.01 

0 

0 

10000 100000 1e+06 1e+07 

10000 100000 1e+06 1e+07 

Freiheitsgrade 



0.06 

0.05 





0.06 

0.05 




0.04 

0.04 

Abbildung3.11:ErgebnisderAuswertungenbeiVerfeinerungmitdemdualenProblem.Links 

0.03 

0.03 

VerfeinerungmitdemZielfunktionalderEnergieoberhalbderAuswertungslinieamEndzeitpunkt, 

0.02 

0.02 

rechtsmitderEnergiedierenzunterhalbderAuswertungslinie,wobeijeweilsdieersten6DatenpunktemitdemEnergiefehlerindikatorgewonnenwurden. 

0.01 

0.01 

0 

0 

10000 100000 1e+06 1e+07 

10000 100000 1e+06 1e+07 



Verhalten.DasausDarstellungsgrundennichtmehrsichtbareweitereVerhaltenderAuswertung desLinienintegralsbeilinearenZielfunktionaldivergiertundnimmtWertegroerals0:2an, wasmitdenzuerwartendenWertenvonetwa0:027zuvergleichenist.Zwarwurdenzuwenige VerfeinerungsschrittemitdemdualenSchatzerdurchgefuhrt,umuberdieKonvergenzendgultige InallenFallenzeigtedieAuswertungnachdemUmschaltennichtdaserwunschtekonvergente 

hochfrequenteRauschenbeimEnergieudurchdieAuswertungslinienachdenzweiHauptpulsen Aussagentreenzukonnen,esdeutenaberandereIndizien,beispielsweisedaswiederzunehmende (vgl.Abbildung3.4),daraufhin,dadieRechnungenauchinweiterenVerfeinerungsschrittennicht konvergierenkonnten. 

zeichnungenverwendet: vergiert,wurdederinAbschnitt2.4.6hergeleiteteAusdruckfurdenLinearisierungsfehlerbei derBestimmungdesEnergieussesdurchdieAuswertungslinie,(2.30),naherungsweisenumerisch ausgewertet.DieErgebnissesindinAbbildung3.13dargestellt;dabeiwurdendiefolgendenBe- 

ZurUntersuchung,weshalbdieVerfeinerungmitdemdualenFehlerschatzersoschlechtkon- 

i:Verfeinerungsstufe; J(w(i) N(i):UberdieZeitschrittesummierteAnzahlvonFreiheitsgraden; h)=(w(i) h):BeidieserVerfeinerungsstufeberechneterEnergieudurchdieKurve; 


0.06 

0.05 



Energie in der hohen Atmosphaere



0.1 

0.08 

0.06 




Lineares Zielfunktional an der Linie 

0.04 

derzumjeweiligendualenFunktionalgehorendenAuswertung. Abbildung3.12:ErgebnisderAuswertungenbeiVerfeinerungmitdemdualenProblem.Vergleich 

0.02 

J(e(i))=J(w)?J(w(i) h):TatsachlicherFehlerbeiAnnahmederExaktheitw=w(8) 

0 

h; 

10000 100000 1e+06 1e+07 


~J(e(i))=RT0RCv(i) seGroekannnurmitHilfedesdualenProblemsunddendamiterhaltenenFehlerschatzern berechnetwerden;beiderLosungderdualenProblemstretenzusatzlicheFehlerauf,diedie ProblemgeschatzterFehler.IneinerSimulationistdieexakteLosungnichtbekanntunddie- 

h(ar(u?u(i) h))n(v?v(i) h)(aru(i) h)ndsdt:Mitdemlinearisierten 

J(e(i))=J(e(i))?~J(e(i)):DierenzzwischenechtemFehlerundmitdemlinearisierten BerechnungdiesesexaktenFehlersoftsehrungenauwerdenlassen.HierwurdedieFehleridentitatohneVerwendungdesdualenProblemsausgewertet,indemfurdieexakteLosung 

heingesetztwurde; FunktionalgeschatztemFehler; diegenauestenumerischeLosungw(8) 

DieDatenentstammeneinerRechnungmitVerfeinerungdurchdenEnergiefehlerindikator;der EnergieufurzweiVerfeinerungsstufenistinAbbildung3.4dargestellt. jJ(e(i))j ZurBestimmungdesLinearisierungsfehlersistdieKenntnisderexaktenprimalenLosung jJ(e(i)j:VerhaltnisvonLinearisierungsfehlerundWertdestatsachlichenFehlers. 

notwendig;dadiesenichtbekanntist,wurdefurw=(u;v)diegenaueste,bekannteLosung w(8) furdieexakteLosungdarstellt,ebensofurdenaufdenerstenBlicknichtgutauskonvergierten EnergieusenbeiverschiedenenVerfeinerungsstufenzueinemerheblichenTeildurchdieOszillationennachdendreiHauptpulsenhervorgerufenwird;derintegrierteEnergieunacht=450s 

h)eingesetzt.Eskanndavonausgegangenwerden,dadieseeineguteSchatzung WertdesEnergieusses(zweiteSpaltederTabelle),dadieUnterschiedeindenauntegrierten h=(u(8) h;v(8) 

betragtfuri=8nurnochrundeinZehnteldesWertesbeii=7undhatnurnocheinenAnteil vonetwazweiProzentamGesamtenergieu.AlsMittelwertausdenverschiedenenAuswertungen beilinearenundkubischenElementenergibtsicheinintegrierterEnergieuvon(6:70:4)108, alsosehrnaheandeminderTabelleverzeichnetenWert,sodadieWahlvonw(8) FehlerzwarmitzunehmenderVerfeinerungkleinerwird(ersollteetwamitderOrdnunghgehen), erscheint. AusderTabellegehthervor,daderLinearisierungsfehlerimVerhaltniszumtatsachlichen hgerechtfertigt

3.4.ERGEBNISSEDERRECHNUNGEN 0i 26.100 N(i) 2:77108 J(w(i) h)J(w)?J(w(i) 3:97108 ?3:381087:35108 ~J(e(i)) J(e(i)) jJ(w)?J(w(i) jJ(e(i))j 1:85h)j45 

1234 52.336.9111:05109 143.491 367.371 62.086 7:16109 5:54109 1:66109 ?6:48109 ?4:86109 ?9:84108 ?1:5710109:24109 ?1:1210106:37109 ?2:901091:92109 1:43 

65.513.3181:02109 934.488 3:01109 ?2:34109 ?3:77108 ?3:46108 ?4:861092:53109 ?8:411084:64108 ?6:871083:41108 1:31 1:95 1:08 1:23 

Abbildung3.13:BestimmungdesLinearisierungsfehlersbeinichtlinearenZielfunktionalen.Man 715.277.8767:91108 842.026.0386:74108 ?1:17108 { ?2:221071:05108 { { 0:99 

beachte,dadieerstendreiDatensatzeimwesentlichenohneAussagesind,dadortdieGesamtenergieummehralseinenFaktorviervomrichtigenWertabweicht,damitauchderEnergieu 

{ 0:90 

zugroistundderVergleichmitJ(w)=(w)(w(8) WeitereErlauterungenimText. h)=J(w(8) h)nichtrealistischseinkann. 

tatsachlichdurch(dieDatenderTabellewurdendurchVerfeinerungmiteinemEnergiefehlerindikatorgewonnen),sozeigendieberechnetenFehlerschatzerkeinerleiKorrelationmitdemFehler, 

abweicht.FuhrtmandieFehlerschatzungundVerfeinerungdurchLosungeinesdualenProblems manmuerwarten,dadienumerischberechnetedualeLosungerheblichvondertatsachlichen Gesamtfehlerliegt.DieLinearisierungumdienumerischeLosungistdaherrechtschlecht,und jedochselbstbeisehrgenauenRechnungenimmernochinderselbenGroenordnungwieder 

denmandurchVergleichmitdergenauestenvorhandenenLosungerwartet,unddieerzeugten GitterzeigenVerfeinerunginGebieten,diefurdieBerechnungderZielgroenichtrelevantsind. GitterverfeinerungundRechnungvonprimalemunddualemProblemnichtkonvergiertundder AnsatzmitdemdualenFehlerschatzerfehlschlagt,istnichtvollstandigklar;insbesondereistnicht klar,weshalbdieeigentlichgutadaptiertenGitterzukeinementsprechendenErgebnisfuhren.Es kommenabereineReiheweitererMoglichkeiteninBetracht,dieimRahmendieserArbeitjedoch ObdieschlechteLinearisierungerklart,weshalbindengerechnetenBeispielenderProzeaus 

wennsienichtimEinugebietdesZielfunktionalsliegen,istzuerwarten,dadieseunerwunschte nichtmehruntersuchtwerdenkonnten.InsbesondereisthierdasProblemzunennen,daWellen GegensatzzumEnergiefehlerindikatorversucht,TeilederWellenaufgrobenGitternzuberechnen, zuverfalschen.InAbschnitt5.4sindeinige,allerdingsunvollstandigeUntersuchungenzumEinu amUbergangzugroberenGitternteilweisereektiertwerden.DaderdualeFehlerschatzerim ReexionrelevanteAusmaeannehmenkann.SiewaredanninderLage,dieErgebnisseerheblich vonGitterunstetigkeitenbeieinemModellfallzunden.GestutztwirddieThese,daReexionan Abbildung3.4gezeigtehochfrequenteRauschennachdenzweiHauptpulsennachderUmschaltung GitterunstetigkeitenderGrundfurdieschlechtenErgebnisseist,vonderBeobachtung,dadasin vomEnergiefehlerindikatoraufdendualenFehlerschatzerwiederzunimmt,wasvongestreuten Wellenverursachtseinkonnte;letztlichistdieseTheseabernichtbewiesenundverlangtnach weiterenUntersuchungen. 3.4.3GlobaleVerfeinerung ZumVergleichsindnochdieerhaltenenWertebeiglobalerVerfeinerungaufgefuhrt.WieAbbildung3.14zuentnehmenist,istderAnteilderEnergie,derdieUbergangsschichtpassiert,deutlich 

ausAbbildung3.4zuvergleichenist;dienochstarkoszillierendeKurveistzwarimVergleichmit niedrigeralsbeidenErgebnissemitadaptiverVerfeinerung.ObwohldieKurverechtachist, denvorhergehendenVerfeinerungsstufendeutlichglatter,abernichtvergleichbarmitdemErgeb- derinAbbildung3.15dargestellteEnergieudurchdieAuswertungslinie,dermitdenErgebnisse kannmandavonausgehen,dasiekeinekonvergiertenWertereprasentieren.DerGrunddafurist


0.06 

0.05 




0.04 

Abbildung3.14:ErgebnissebeiglobalerVerfeinerung. 

0.03 

0.02 

0.01 

0 

10000 100000 1e+06 1e+07 1e+08 



4e+07 

3 Verfeinerungen, 1.130.391 Freiheitsgrade 

3e+07 

4e+07 

6 Verfeinerungen, 68.890.950 Freiheitsgrade 

3e+07 

46 nisderfeinstenadaptivenRechnung.DieOszillationstammt,wieinAbbildung3.4links,von einemzugrobenGitter;derglattereVerlaufliegtinderAbwesenheitderbeiadaptivenRechnungenvorhandenenStorungendurchGitteranderungenbegrundet.Besondersbemerkenswertist 

derunphysikalischeunddamitoensichtlichfalschezeitweiligenegativeEnergieu,derbeiden 

KAPITEL3.ANWENDUNGAUFDIESOLAREATMOSPHARE 

adaptivenRechnungenauchnichtauftritt. 

2e+07 

2e+07 

1e+07 

1e+07 

Abbildung3.15:EnergieudurchdieAuswertungslinieinAbhangigkeitvonderZeitbeiverschiedenenVerfeinerungsstufen.DieVerfeinerunggeschahdurchglobaleVerfeinerung.Manvergleiche 

dieErgebnissemitdenenausAbbildung3.4,diemitdeutlichwenigerFreiheitsgradengewonnen 

0 

0 

-1e+07 

-1e+07 

wurden. 

-2e+07 

-2e+07 

-3e+07 

-3e+07 

0 100 200 300 400 500 600 700 

0 100 200 300 400 500 600 700 

AusdengenanntenGrundenmudavonausgegangenwerden,danocherheblichmehralsdie 

[s] 

[s] 

verwendeten68.000.000Freiheitsgradenotigwaren,umeinvergleichbaresErgebniswiebeiden adaptivenRechnungenzuerhalten;diesewurdenfreilichmitmaximalrund42.000.000FreiheitsgradenerzieltmoglichkeitenpraktischdieselbenWerteergeben.DasliegteinerseitsanderEnergieerhaltung 

inAbwesenheitvonGitteranderungen(dasbegrundetdieGleichheitderErgebnissederEnergieauswertungober-undunterhalbderLinie),bedeutetaberandererseitsauch,dapraktischder 

gesamteEnergieaustauschzwischendenbeidenTeilendesGebietsdurchdieAuswertungslinie BemerkenswertandenErgebnissenausAbbildung3.14istnoch,dadiedreiAuswertungs- 

stattndet.LetzteresistangesichtsderglobalenKopplungderinjedemZeitschrittzulosenden elliptischenGleichungnichtselbstverstandlich;insbesonderezeigendieErgebnisseadaptiverRechnungen,dadurchGitteranderungEnergieauchnichtlokalaufdemGitterverteiltwird,wasdazu 

vorhandeneEnergieunterscheiden. fuhrt,dasichauntegrierterEnergieudurchdieAuswertungslinieunddieoberhalbdieserLinie 

Energiefluss in willkuerlichen Einheiten

Kapitel4 

Implementation TechnischeAspekteder 

DazugehoreninsbesonderedieBehandlunghangenderKnoten,aberauchderTransfervonFinite- folgtimwesentlichen[22,4,5].DerTransferzwischenGitternistparallelzu[19]implementiert. dienichtzudenublichenStandardtechnikenbeiProgrammierungmitnitenElementengehoren. Elemente-FunktionenvoneinemGitterzueinemanderen.DieBehandlungvonhangendenKnoten IndiesemKapitelsindeinigederAspektederImplementationdesProblemskurzbeschrieben, 

4.1 EineausfuhrlichetechnischeReferenzderdeal.II-Bibliothekistunter[3]zunden. 

DasProgramm,dasdieindieserArbeitbeschriebenenMethodenimplementiert,basiertaufder parallelzurArbeitentstandenenBibliothekdeal.II.SieistimwesentlicheneineNeuimplementationeinigerVerfahren,dieanhandderamInstitutfurAngewandteMathematikindenletzten 

Diedeal.II-Bibliothek 

JahrenentwickeltenBibliothekDEALentwickeltwurden,d.h.insbesonderedieVerwendungvon hangendenKnotenbeihierarchischenGitternunddieVerwendungvonFehlerschatzkonzeptenzur adaptivenGitterverfeinerung.VonDEALunterscheidetsiesichjedochinwesentlichenPunkten, darunterunteranderem: VerschiedeneFiniteElemente:EswurdeeineSchnittstelledeniert,dieeserlaubtnahezu beliebigeElementtypenzuimplementieren.DazumuderBibliotheklediglichdiefolgende Informationbekanntgegebenwerden: {wievieleFreiheitsgradeeinElementproKnoten,KanteundZellehat; {wiedieInterpolationentlangvonKantenzuerfolgenhat,anderZellenunterschiedlicher 

MitdiesenInformationenkanndieBibliothekdieVerteilungvonFreiheitsgraden,dieBe- 

{wiedieInterpolations-undProlongationsmatrizenzwischenZellenundihrenKindern aussehen. Groezusammenkommen; 

rechnungvonNebenbedingungenfurhangendeKnotenu.a.vornehmen,ohneuberdasver- 

wendeteElementgenauerBescheidzuwissen. lokaleMassematrizen,usw.derBasisfunktionenzuruckliefern.DieseFunktionenhabenebenfallseinheitlicheNamen,sodaesmoglichist,ProgrammeohneKenntnisdesverwendeten 

ElementszuschreibenunddieAuswahldesElementszurLaufzeitvorzunehmen. ImMomentsindLagrange-ElementemitlinearenbisquartischenAnsatzgraden,sowieein spezielleresElementimplementiert. 

FurdieNumeriksindeineReihevonFunktionenzuimplementieren,dieWerte,Ableitungen, 

47

48Dimensionsunabhangigkeit:DiemeistenProgrammelassensichdimensionsunabhangigfor- 

mulieren,wennmanberucksichtigt,daOperationenimallgemeinenaufZellenundihren KAPITEL4.TECHNISCHEASPEKTEDERIMPLEMENTATION 

Seitenstattnden.DieBibliothekunterstutztdies,indemsienebendenDatentypenHex, 

DiebeiweitemmeistenAlgorithmeninAnwenderprogrammenundderBibliotheklassensich zweiDimensionenuberVierecke,indreiDimensionenuberHexaedergeht. QuadundLineauchlogischeTypenwieCellundFacedeniert.Diesewerdenjenachder 

aufdieseWeisedimensionsunabhangigschreibenundsindineiner,zweiunddreiDimensio- 

verwendetenDimensionaufdierichtigenObjektegesetzt,sodaeineSchleifeuberZellenin 

nenohneAnderunglauahig.DiesvereinfachtnichtnurdieProgrammierungsondernverrin- 

gertdurchWiederverwendungvonProgrammteilenaucherheblichdasRisikovonFehlern,da ModerneProgrammiertechniken:DurchdieVerwendungvonindenletztenJahrenentwickeltenProgrammiertechniken,insbesondereTemplatesundIteratorenunddurchdieNutzung 

nichtdiegleichenAlgorithmeninverschiedenenVersionenfurunterschiedlicheDimensionen gewartetwerdenmussen. 

einfacherundwenigerfehleranfallig;erstdieNutzungdieserMoglichkeitenhateserlaubt, derStandardTemplateLibraryvonC++istdieProgrammierungderBibliothekerheblich dimensionsunabhangigeAlgorithmenzuschreiben. DaruberhinausmachtdieBibliothekwesentlichmehralsDEALvonFehlerabfragenzur 

4.2genundausgetesteteProgrammekanndieFehlerprufungausgeschaltetwerden. 

LaufzeitGebrauch,umProgrammierfehlerfruhzeitigzuerkennen.FurProduktionsrechnun- 

BeiderDiskretisierungistinjedemZeitschritteineGleichungdesfolgendenTypszulosen: TransfervoneinemGitterzumanderen 

DieFaktoren,undspielenindiesemAbschnittkeineRolle.MitnitenElementenimRaum diskretisiertergibtsichdiefolgendeAufgabe:Sucheu1h2V1,sodafuralle (+A)u1=u0+kv0?Au0: 

gilt.Dabeisindu0h;v0h2V0,undV0undV1seiendieAnsatzraumeaufdenGitternzumvorigen (u1h; 1)+a(u1h; 1)=(u0h; 1)+k(v0h; 1)?a(u0h; 1) 12V1 

undzumaktuellenZeitschritt. SchreibtmandasProblemineinGleichungssystemum,soergibtsich (4.1) 

mitdenMatrizen (M1ij+A1ij)u1j=M10 M1ij=(1i;1j); iju0j+kM10 ijv0j?A10 iju0j 

M10 A1ij=(r1i;r1j); 

Dabeisinddie0j2V0;1j2V1dieBasisfunktionenderjeweiligenFinite-Element-Raume. A10 ij=(1i;0j) ij=(r1i;r0j): und 

wennsiezellweisedurchgefuhrtwird.FurdieAufstellungderanderenMatrizenspaltenwirdie Zeitschritt. enZeitschrittsind,giltM10;A102Rn1n0,mitn0derDimensiondesAnsatzraumeszumalten WahrendM1;A12Rn1n1quadratischeMatrizenderDimensionn1desAnsatzraumszumneu- 

IntegrationuberZellenauf:M10 DieAufstellungderMatrizenM1;A1istStandardundbietetkeinebesonderenSchwierigkeiten, ij=XK2T(1i;0j)K=XK2TM10;K

DabeiseiTeineTriangulierungdesGebietsso,dajedesK2TsowohlinT0alsauchinT1 enthaltenist,wobeiTndieTriangulationdesGebietsimntenZeitschrittdeniere;Kindervon 4.3.BEHANDLUNGVONDIRICHLET-RANDWERTEN 49 

KseienhochstensineinemderbeidenGitterenthalten.AnschaulichistTdieMengederjeweils feinstenZellen,dieinbeidenGitternochenthaltensind.ZurIllustrationfordernwir,dasichdie ZellenderbeidenGitterumhochstenseinVerfeinerungslevelunterscheidendurfen,d.h.dajedes K2TentwederaufkeinemderbeidenGitterKinderhatoderaufgenaueinemderbeidenGitter genaueinmalverfeinertist.DieseEinschrankungisthiernurderEinfachheithalbergemacht;VerfeinerungenubermehrereStufensindmoglichundwerdenrekursivmitdemuntenbeschriebenen 

Verfahrengehandhabt. 1.KistaufkeinemderbeidenGitterweiterverfeinert;dannistdim(V1jK)=dim(V0jK)und BeinureinerVerfeinerunggibtesdreiFallezuunterscheiden: 

2.KistaufT0einmalverfeinert;dannistdim(V1jK)dim(V0jK).FurkonformeAnsatze DieFalle2und3sindetwasaufwendiger.FurgeschachtelteAnsatzraumelieesichbeispiels- 

miteinerSchachtelungderAnsatzraumegilthierV1jKV0jK. 

mitf0lgl2LderMengeallerBasisfunktionenmitTrageraufK.DieMatrixcilistunabhangigvon Kundkonstant.DamitlatsichM10;K ij1ijK=Xl2Lcil0ljK; durcheineSummeuberdieKindzellenvonKschreiben: (4.2) 

=Xk2KXl2Lcil(0l;0j)k =Xl2Lcil(0l;0j)K =(1i;0j)K 

wobeiKdieMengederKindzellenvonKdarstelle.DieBerechnungvonM10;K =Xk2KXl2LcilM0;k lj; 

KnuraufT1verfeinertist,gehtganzanalog,indemman0ientsprechend(4.2)durchdie1l ausdruckt. aufeineSummationuberzellweiseMassematrizenzuruckgefuhrt.Derumgekehrte,dritteFall,da DieDarstellung(4.2)setztvoraus,daV1jKV0jK,dasheitdasichjedeBasisfunktion ij istsomitwieder 

ArbeitverwendetenLagrange-Elementenimmergegeben.BeianderenFinite-Elemente-Klassen durchdieBasisfunktionenaufhoherenVerfeinerungslevelndarstellenlat.Dasistbeidenindieser istdieAufstellungderrechtenSeitevon(4.1)nichtsoeinfachundimallgemeinenauchnichtexakt durchzufuhren,daQuadraturenverwendetwerdenmussen. 

chung 4.3 ZurIllustrationderBehandlungvonDirichlet-RandwertenbetrachtenwirbeispielhaftdieGlei- 

?u=f u=g x2@: x2;

50 KAPITEL4.TECHNISCHEASPEKTEDERIMPLEMENTATION 

DurchWahleinerFunktionu0mitu0=gauf@latsichebensogutdasfolgendeProblemlosen: 

suche~u=u?u0,soda?u=f+u0 

x2; 

u=0 x2@ 

gilt.DieRandwertesinddamithomogengeworden.IndenmeistenFallenistdieRandfunktiong 

nichtdurchdieSpureinerFinite-Elemente-Funktionu0;hdarstellbar,sodamanmiteinerapproximativenBehandlungderRandwerteauskommenmu,beispielsweisedurchVerwendungeiner 

ProjektionoderInterpolationaufdieSpurdesAnsatzraumes,~g=PV0goder~g=IV0g,unddie 

dazugehorigeFunktion~u0.InderPraxisistdieWahleinergeeignetenFunktion~u0jedochunpraktisch;stattdessengibteszweiAnsatzezurdirektenBehandlungderursprunglichenGleichung,die 

beidedaraufberuhen,SystemmatrixundrechteSeiteaufallenZellendesGebietsunddamitmit 

allenFreiheitsgradenaufzubauenundanschlieenddendurchdieRandbedingungenfestgelegten 

FreiheitsgradenaufdemRandeinespezielleBehandlungzukommenzulassen: 

Filtern:dieseMethodebietetsichan,wenndielinearenGleichungendurchiterativeVerfahren 

gelostwerden.DiemeisteniterativenLoserlassensichalsDefektkorrekturverfahrenschreiben,das 

heiteswirdeinAnfangswertberechnet,deranschlieendjeweilsnurnochdurchadditiveKorrekturenverandertwird.DasFilternfunktioniertnunso,damandemStartvektordierichtigen 

WertefurdieFreiheitsgradeaufdemRandaufzwingtundbeidenKorrekturvektorendieEintrage 

furdieseFreiheitsgradejeweilsaufNullsetzt(ltern),waseinermodiziertenMatrix-Vektor- 

Multiplikationentspricht,diederMultiplikationmitderSystemmatrixausdemmodizierten 

Problementspricht. 

DieserAnsatzwurdeindealgewahlt.EristinvielenFallen,wonurwenigeIterationenzur 

Losunggebrauchtwerden,bedeutendschnelleralsderzweiteWeg,verlangtabervielSorgfaltbei 

derImplementationderlinearenAlgebra. 

EliminationausderMatrix:dieseMethodeistbeiallenLosernmoglich,insbesondereauchfur 

direkteLoser.Sieberuhtdarauf,dadiebetroenenFreiheitsgradetatsachlichausderMatrixund 

derrechtenSeiteeliminiertwerden,wodurchsichdieDimensiondeslinearenGleichungssystemsauf 

dieAnzahldertatsachlichfreienFreiheitsgradereduziert.DadasUmkopierenineineneue,kleinere 

MatrixundeinenentsprechendenVektorzuunpraktischundmitzugroemSpeicheraufwand 

verbundenware,gehtmanwiefolgtvor:furjedenFreiheitsgradaufdemRandwirdzuerstdie 

entsprechendeZeileausderMatrixgestrichen,lediglichderDiagonaleintragbleibtstehen.Der 

WertderrechtenSeitewirdsogesetzt,daderLosungsvektordenrichtigenWertbekommt.Da 

indieserZeilenunnurnocheineinzigerEintragsteht,istderWertdesFreiheitsgradestatsachlich 

festgelegt.UmdieMatrixwiederpositivdenitundvorallemsymmetrischzumachenwirdnunmit 

dieserZeileeinGau-Eliminations-Schrittgemacht,umauchalleEintragederentsprechenden 

SpaltezuNullzumachen;dabeiwirdauchdierechteSeiteentsprechendmodiziert.Durchden 

EliminationsschrittistderFreiheitsgradvomRestdesGleichungssystemsabgekoppelt. 

FureinigeIterationsverfahrenistdieDurchfuhrungdesEliminationsschrittsnichteinmalnotig, 

wiemansichuberlegenkann.DerAllgemeinheithalberwurdeaberkeinGebrauchvondieser 

Tatsachegemacht. 

SchreibtmansichdasVerfahrengenauhin,dannentsprechenMatrixundVektorabgesehenvon 

denzusatzlichenZeilenundSpaltengenaudenen,dieentstundenwennmandasobenbeschriebene 

modiziertekontinuierlicheProblemlosenwurde,wobeifur~u0dieFunktiongewahltwird,dienur 

aufderauerstenSchichtvonZellenlebtundaufdemganzenGebietstetigist(dieseFunktionist 

eindeutig). 

DerbeschriebeneWegwurdeindeal.IIgewahlt.EristetwasallgemeineralsdasFiltern,hat 

jedochdenNachteil,daderEliminationsschrittinschwachbesetztenMatrizenmiterheblichem 

RechenaufwandindenverteiltenDatenstrukturenverbundenist.VomStandpunktderRechenzeitlohntersichnurfurgroereProbleme,beidenenvieleIterationsschrittenotigsind,dader 

AufwandfurdasFilterninjedemSchrittanfallt,wahrenddieEliminationnureinmalnotigist.In 

derSummeistderImplementationsaufwandwohlgeringer,daerzentraleinmalbereitgestelltwird 

undnichtfurjedenFalldieMatrix-Vektor-Multiplikationmodiziertwerdenmu.Daruberhinaus

4.4.BEHANDLUNGVONHANGENDENKNOTENIMORT 51 

~'1 ~'2 

~'3 '2 

Abbildung4.1:SchemazurEliminationvonhangendenKnoten(links).Die'unechtenÀnsatzfunktionen~'1,~'2und~'3,sowiedie'echteÀnsatzfunktion'2 

istesdurchdiezentraleBereitstellungmoglich,einegutoptimierteImplementationanzubieten, dievonderinternenEigenschaftvonverschiedenenMatrizentypenGebrauchmacht,wasbeiAnwenderprogrammennichtsinnvollwareundsomitbeimFilternnichtgeht. 

dieimMomentimplementiertenVerfahren. aufdieRestriktiondesFinite-Elemente-RaumsaufdenRandbestimmt.DieInterpolationwurde Wederdealnochdeal.IIsindaufdiejeweilsbeschriebeneMethodefestgelegt;essindlediglich 

hierderL2-Projektionvorgezogen,dadieBerechnungderProjektionbeigekrummtenRandern aufwendigerist.AndererseitsistdieProjektionbeiunstetigenRandwertenunumganglich,um dieKonvergenzordnungzuerhalten;aufgrundderfurdieseArbeitvorausgesetztenGlattheitder DieWertederzueliminierendenFreiheitsgradewerdengemaderInterpolationderRandwerte 

RandwerteistdieInterpolationaberausreichend. 

denWertenzumvorigenZeitschritt.ImletzterenFalllassensichdannwiederdiebeidenoben derenRandbedingungen,beispielsweiseabsorbierendeRandbedingungen,lassensichebensobe- 

handeln,odersieerlaubendieBerechnungvonWertenfurdieFreiheitsgradeaufdemRandaus linearforma(;)undbedarfkeineManipulationderlinearenGleichungssysteme.Diemeistenan- 

DieBehandlungvonNeumann-RandwertengeschiehtdurchdieWahleinermodiziertenBi- 

angefuhrtenTechnikenverwenden. 4.4 BeiderVerwendungvonGitternmithierarchischerVerfeinerungeinzelnerZellenohneVerwendungvonAbfangelementenbleibenaufdenSchnittstellenzwischenverfeinertenundunverfeinerten 

BereichenhangendeFreiheitsgradezuruck.UmbeidenverwendetenkonformenFinite-Elemente- BehandlungvonhangendenKnotenimOrt 

AnsatzenvernunftigeLosungenzugarantieren,muandiesenStellendafurgesorgtwerden,da dieLosungsfunktionstetigbleibt. heithalbervonbilinearenElementenausgegangensei.DieBehandlunghohererAnsatzgradeund hohererDimensionenalszweiverlauftganzanalog,jedochsinddieGleichungenwenigerubersichtlichḊa,wiegesagt,dieFunktionamKnoten3stetigseinsoll,muwegenderLinearitatder 

DieBehandlungderhangendenKnotenseianAbbildung4.1illustriert,wobeiderEinfach- 

MittelwertderKoezientenderKnoten1und2sein.ImPunkt3bendetsichdamitkeinechter AnsatzfunktionenaufdenKantenderKoezientderBasisfunktionzumKnoten3genauder 

1 

2 

3 

1 

3 

2

Freiheitsgrad,ausalgorithmischenGrundenwerdenaberMatrizenundVektorensoaufgebautals 52 waredorteiner,dasichdannMatrizenundVektorenzellweiseaufbauenlassen,ohnedaschon KAPITEL4.TECHNISCHEASPEKTEDERIMPLEMENTATION 

beimAufbauRucksichtaufdiehangendenKnotengenommenwerdenmu.Ineinemzweiten SchrittwerdenindenVektorendieEintragezurBasisfunktion3jeweilshalftigaufdieEintrage zudenBasisfunktionen1und2verteilt.AnalogwerdenindenMatrizendieSpaltenundZeilen hangendenKnotengehorigeZeileundSpaltewirdaufNullgesetztumdenunechtenFreiheitsgrad zurBasisfunktion3aufdieZeilenundSpaltenderanderenBasisfunktionenverteilt.Diezum vomRestdesSystemszuisolieren. und'2zudenPunkten1und2habenihrenTragerjeweilsaufdenElementen1bis3,wieman erwartenwurdewennderhangendeKnoten3garnichtdaware.DieseBasisfunktionenlassen sichjedochdurchdieBasisfunktionen~'1und~'2zudenentsprechendenPunktenplusjeweilsder HalftederBasisfunktion~'3zummittlerenKnotendarstellen: AnschaulichistdiesesVorgehenfolgendermassenverstandlich:dieechtenBasisfunktionen'1 

'2=~'2+12~'3: '1=~'1+12~'3; 

auf,dasheitmitdenBasisfunktionen~'i,soistklar,wiedieanschlieendeAufsummierungzu denMatrizenmitdenechtenBasisfunktionen'jstattzundenhat.InhoherenDimensionenoder und3.BautmannunMatrizenundVektorenaufdenZellenohneWissenuberhangendeKnoten beihoherenAnsatzgradenlassensichdieAnsatzfunktionenaufdereingeschranktenKantedurch ~'1und~'2habenihreTrageraufdenZellen1und2bzw.1und3,~'3lebtaufdenElementen2 

eineMatrix 

zenundVektorendimensions-undansatzgradunabhangigaufreinalgebraischerBasisdurchgefuhrt mitdenunechtenFreiheitsgradenaufdenTeilkantenverknupfen,sodadieEliminationausMatri- 

'i=Xjcij~'j 

werdenkann. PrinzipanalogzurBehandlungvonRandwertendurchfuhrbar.Eskommenwiederdiebeiden (Kondensation)gewahltwurde.NachdemLosenderGleichungssystemeistdaraufzuachten,die Freiheitsgradewiederzuverteilen,dasheitdenEintragzumKnoten3aufdieHalftederEintrage MoglichkeitenFilternunddirekteManipulationinFrage,wobeiindeal.IIdiedirekteElimination DieImplementationderobenbeschriebenenManipulationvonMatrizenundVektorenistim 

4.5 derbeidenbenachbartenFreiheitsgradezusetzen. 

DievernunftigeSteuerungderGitteraufdenverschiedenenZeitebenenisteinThemauberdasalleinewohlDiplomarbeitenzuschreibenwaren.ImfolgendenAbschnittsolleneinigederProbleme 

SteuerungdesGitters unddieunternommenenVersuchezurLosungkurzbeschriebenwerden.Siesindimwesentlichen 

4.5.1AuseinanderdriftenderGitter metern,sodadiesenichtbeiallenBeispielenangegebensind. unabhangigvonZeitschrittverfahren,Verfeinerungskriterium,FehlerschatzerundahnlichenPara- 

zuverfeinernden/zuvergroberndenZellenbestimmtunddarausGitterTnh1erzeugt,diejetztauf GitterTh0,dasinallenZeitschrittenidentischist,werdendieLosungenwh0undwh0desVorwartsundRuckwartsproblemsberechnet.AusdiesenbeidenLosungenwerdenfurjedenZeitschrittdie 

DieErzeugungvonGitternndetimwesentlichenwiefolgtstatt:aufeinemgegebenengroben

Anzahl an Zellen 

7000 

6000 

5000 

Durchlauf 0 

Durchlauf 1 

Durchlauf 2 

Durchlauf 3 

Durchlauf 4 

Anzahl an Zellen 

deneinzelnenZeitschrittennimallgemeinenunterschiedlichsind.AufdiesenGitternwerdenjetzt wiederdieLosungenuh1undzh1berechnet,darausdieGitterTnh2,usw. 4.5.STEUERUNGDESGITTERS 53 

dieseArtbestehtpraktischkeineKopplungzwischendenGitternzuverschiedenenZeitschritten blem,wennsichdieVerfeinerungsleveleinigerZellenzwischendenbeidenGitternzustarkandern, undinderTatunterscheidensichdieGitterTnhlundTn+1 dadanndieProjektionderLosungvomaltenGitteraufdasneueleidet(technischisteinTransfer ImEndeektwirdjedesGitterTnhlausTnhl?1unddenLosungenwnhl?1undwnhl?1bestimmt.Auf 

ubermehrereVerfeinerungsebenenohneweiteresmoglich,wieinAbschnitt4.2beschrieben). hloftbetrachtlich.DasistdanneinPro- 

4000 

4000 

3000 

3000 

Abbildung4.2:AnzahlanGitterzelleninverschiedenenDurchlaufen.DieGitterentstandendurch VerfeinerungnacheinemEnergiefehlerschatzerbeimeinemBeispiel,beidemeineWellevomRand 

2000 

2000 

1000 

1000 

sehrklein;dieRandbedingungensindabt=0:4konstantNull,sodasichdieWellenurverschiebt ausdurchdasGebietlauft.DadieAnfangsbedingungenkonstantsind,istdieZellzahlamAnfang 

0 

0 

unddieZellzahlinetwakonstantbleibensollte.LinksistnurdieAnzahlderVerfeinerungslevel 

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 

0 0.2 0.4 0.6 0.8 1 

Zeit 

Zeit 

begrenzt,umdiesicheinzelneZelleninaufeinanderfolgendenZeitschrittenunterscheidendurfen, rechtssindallebeschriebenenKopplungenzwischenaufeinanderfolgendenGitternverwendet.Die 

markiert,umzuverhindern,dasichdieVerfeinerungsstufenzweierZelleninaufeinanderfolgendenGitternummehralseinsunterscheiden1undeswurdeneinigeGitterglattungsalgorithmen 

implementiert,umisolierteverfeinerteoderunverfeinerteZellenundeinigezusatzlicheFallezu UmdieDivergenzderGitterzuverringern,wurdeversucht,dieTnhlfuraufeinanderfolgende nmoglichstenganeinanderzukoppeln.DazuwerdenjeweilszusatzlicheZellenzurVerfeinerung absoluteZahlderZellenistaufgrundunterschiedlicherVerfeinerungsparameternichtvergleichbar. 

zillationenindenerstenDurchlaufenverstarkensichindendarauffolgenden,sodaVariationen eliminieren.DurchdieseSchrittewurdedasGitterTnhlaueranTnhl?1auchandieGitterTn1 einzelnenGitternbleibtimwesentlichenaberunkorreliert,wieAbbildung4.2zeigt.KleineOs- 

gekoppelt.DasdampftzwardieschlimmstenDivergenzenetwas,dieAnzahlanZelleninden derZellzahlinaufeinanderfolgendenZeitschrittenbiszueinemFaktorzweidurchausvorkommen, 

beivieroderfunfZeitschrittenauseinanderliegendenGitternauchFaktorendreiodernochmehr; ahnlicheOszillationenwurdenauchvonHartmann[19]beobachtet.EinMechanismusscheintzu 

hieristalgorithmischerNatur,weilkeinvernunftigesKriteriumfurdenAbstandzweierGitter Durchlaufmoglich,zumBeispielindemTnhlauchanTn2 sein,dadieKopplungdieGitterfureinigeZeiteinigermaenkonstanthalt,bissiesichruckartig andern. 

voneinanderundseineBegrenzungbekanntscheint.ZuengdurfendieGitteraufderanderenSeite auchnichtaneinandergekoppeltsein,dasonstdieVorteiledesmitwanderndenGittersverloren EineLosungdiesesProblemsistwohlnurdurcheinestarkereKopplungderGitterinjedem hlgekoppeltwird.DieSchwierigkeit 

verandertwerdenkann,wasdannaberunterUmstandenAuswirkungenaufdasGitterzumZeitschrittn?1haben konnte.SolcheAnderungenubermehralseinenZeitschrittwerdenausalgorithmischenGrundennichtbeachtet undkonnendazufuhren,dasichGitterummehralseineVerfeinerungsebeneunterscheiden. 1DieseBedingunglatsichnichtimmergarantieren,dadasGitterineinemZeitschrittnvomdarauffolgenden 

7000 

6000 

5000 

Durchlauf 0 

Durchlauf 1 

Durchlauf 2 

Durchlauf 3 

Durchlauf 4

gehen;sofuhrtbeispielsweisedieLimitierungderDierenzderVerfeinerungsleveleinzelnerZellen 54 desaktuellenGittersmitdemvorletzten(stattnurmitdemletzten)Gitterimwesentlichenzu KAPITEL4.TECHNISCHEASPEKTEDERIMPLEMENTATION 

einemEinfrierenderGitter,wasnichterwunschtseinkann. 

wohlzugrob,umwirklichezientzuarbeiten,2weshalbauchkompliziertereVerfahrenuntersucht Abbildung4.2wurdeninjedemZeitschrittdieZellenmitdemgrotenFehlerbeitragzurVerfeinerungmarkiert,diezusammenqr=95ProzentdesFehlersausmachen,wahrenddieZellenzur 

EinandererAnsatzwaredieVerwendunggeeignetererVerfeinerungskriterien.ImBeispielin Vergroberungmarkiertwurden,diedieunterenqc=2Prozentausmachen.DiesesVerfahrenist wurden. diewesentlichbessere,jedochnochnichtvolligbefriedigendeErgebnisseliefert.EinBeispielistin Abbildung4.2rechtswiedergegeben,beidemdieZellzahlinetwadementspricht,wasmangerne hatte;dieVerlaufesindallerdingsnichtinallenFallensogut.DieRegelnzurGittersteuerungsind imfolgendenalsPseudoprogrammangegeben: InErmangelungfundiertererAnsatzewurdeeineAnzahlheuristischerRegelnimplementiert, 

1.MarkieredieZellenmitdemgrotenFehlerKzurVerfeinerung,diezusammendenAnteil 2.MarkieredieZellenmitdemkleinstenFehlerKzurVergroberung,diezusammendenAnteil qramGesamtfehlerhaben. 

3.LoschedieVergoberungsagsvonZellen,beidenennichtalleKindereinerZellemarkiert qcamGesamtfehlerhaben. 

4.MarkierezusatzlicheZellen,sodadasaktuelleunddasGitterdesletztenZeitschrittes sind. 

5.MarkiereindiesemundimletztenGitterzusatzlicheZellen,sodasichdiebeidenGitter umjeweilshochsteneineVerfeinerungsstufeaufjederZelleunterscheiden. gewissenRegularitatsforderungengenugen. 

6.WennimerstenVerfeinerungsdurchlauf,dannEnde. 7.ZahledieAnzahlenNnundNn?1derdurchdieMarkierungenaufdiesemundaufdem 8.BerechneeineobereunduntereSchrankefurdieAnzahlanZellenimaktuellenGittergema letztenGitterentstehendenZellen. 

FallsimerstenVerfeinerungsdurchlaufoderdiealteZellzahlaufdemaktuellenGitterkleiner folgenderFormeln:Nnmax=Nn?1(1+"); als200ist,verwende3"#statt"#.FallsimzweitenDurchlaufoderdieZellzahlkleinerals 300,dannverwende2"#. Nnmin=Nn?1(1?#): 

10.Sonst:FallsNnNnmin. 9.FallsNn>NnmaxundNn>200,dannloschesolangeVerfeinerungsmarkierungen,bisNn< 

11.FuhredieSchritte3,4und5erneutaus. Nnmax. 

WertallerdingsnurfureinfachestatischeProblemealsgutgilt,brauchtemanauchwesentlichmehrVerfeinerungsdurchlaufe,umzumletztendlichbrauchbarenGitterzugelangen,wasausRechenzeitgrundennichtpraktikabel 

12.FallsnichtNnmin

4.5.STEUERUNGDESGITTERS 55 

DieVariationvon"#inPunkt8istnotwendig,umdasGitterindenerstenVerfeinerungsschrittennichtzustarkeinzuschranken.AufgrundderinSchritt11durchgefuhrtenAktionenist 

nichtmehrgarantiert,dasichdieZellzahlNnimZielkorridor[Nnmin;Nnmax]bendet,sodaim 

letztenSchritteineIterationgestartetwird;imallgemeinensindzweiDurchlaufederPunkte7 

bis11ausreichend.Alsgeeignetfur"und#habensichWerteinderGegendvon0.1und0.03 

erwiesen.#solltekleinerals"sein,dadieApproximationbeieinerVerkleinerungderZellzahl 

leidet,wahrendeineVergroerungimallgemeinenkeinenegativenAuswirkungenhat."sollte 

trotzdemnichtzugrosein,dafurdasdualeProblemdieumgekehrteZeitrichtunggiltundda 

einzustarkerAnstiegimallgemeineneinestarkeVerkleinerungderZellzahlnachsichzieht. 

ZurBerechnungderFehlergroeKwirdentwedereinEnergiefehlerindikatoroderderduale 

Fehlerschatzerverwendet.BeidemessenjedochnurdenFehlerinderprimalenLosung.Sollder 

dualeFehlerschatzerverwendetwerden,soistesnotwendig,daauchdiedualeLosungmithinreichenderGenauigkeitberechnetwird;eswirddaherderEnergiefehlerindikatorauchaufdieduale 

Losungangewendet,diezellweisenFehlergroendKausdiesemProzegeeignetskaliert,soda 

dermaximaleFehlerproZellemaxKpKausdemprimalenProblemundmaxKdKausdemdualen 

ProblemgleichgrosindundschlielichwirdausdiesenbeidenGroeneinegewichteteSumme 

gebildet,diealsVerfeinerungskriteriumverwendetwird: 

K=pK+maxK0pK0 

maxK0dK0dK 

InderPraxishatessicherwiesen,daeinegeeigneteGewichtungdenprimalenFehlerschatzer 

etwa=4bis8MalsostarkbewertetwiedendualenIndikator.BeiderBerechnungderSprunge 

derNormalenableitungfurdenEnergiefehlerschatzeristbeimdualenProblemdieVariablevhzu 

verwenden,wiemanaus(2.21)erkennt. 

AusdemgleichenGrundwieobenistesbeinichtlinearenZielfunktionalen,beideneneine 

LinearisierungumdienumerischerhalteneLosungnotwendigist,wichtig,dadieerstenVerfeinerungsschrittemiteinemEnergiefehlerschatzerstattdemdualenSchatzerdurchgefuhrtwerden. 

ImanderenFallkannespassieren,dadiedualeLosungaufgrunddermangelndenGenauigkeit 

dernumerischenprimalenLosungstarkvonderLosungdesexaktendualenProblemsabweicht. 

DieVerfeinerungwirddanninGebietendurchgefuhrt,diefurdasErgebnisnichtrelevantsind,so 

dadieprimaleLosungimnachstenSchrittgenausofalschistwieimersten;dasVerfeinerungsverfahrenkonvergiertdannnicht. 

DieVerwendungvorgelagerterVerfeinerungsschrittemiteinemEnergiefehlerindikatorwidersprichtabernichtdemAnsatz,dieAdaptivitatmiteinemdualenProblemanzugehen;derGrund 

ist,dadieLosbarkeiteinesProblemsaufeinebestimmteGenauigkeitpraktischausschlielich 

durchdievondenletzteneinbiszweiVerfeinerungsdurchgangenbenotigtenRessourcen(RechenzeitundSpeicher)bestimmtist,wahrenddiedavorliegendenDurchgangeweitgehendvernachlassigbarsind.GelingtesalsomiteinemdualenProblemdenbenotigtenmaximalenRessourcenbedarfzusenken,soistdieVerwendungsuboptimalerVerfahrenindenvorherigenadaptiven 

Schrittenakzeptabel. 

DasVerfahrenzurSteuerungderZellzahlistinderbeschriebenenFormnichtganzbefriedigend. 

DerGrundliegtdarin,daderAlgorithmusversagt,sobaldderZeitschrittsehrkleinwird,dadie 

Abweichungen"#eigentlichproportionalzurZeitschrittweiteseinsollten,umeineBeschrankung 

derAnderungsratezugarantieren.Problematischdabeiist,daderZielkorridorfurdieZellzahl 

nichtkleineralsetwafunfProzentseinsollte,dadieresultierendeZellzahlbeiMarkierungeiniger 

Zellennichtgenauvorhersagbaristundessonstnichtmoglichist,dasZielzuerreichen.Losen 

latsichdiesesProblemnurbeiKopplungvonmehralszweiZeitschrittenaneinander. 

4.5.2h-AbhangigkeitderDispersionsrelation 

EinesderinderPraxisunangenehmstenProblemeistdieAbhangigkeitderAusbreitungsgeschwindigkeitvonderlokalenGitterweite.DiesesProblemistwohlbekanntundauchtheoretischgut 

untersucht,siehezumBeispiel[1].DerEektistbesondersausgepragtfurlineareElemente.Im

daWellenaufgroberenGitternschnellerlaufenalsauffeinenunddadieGeschwindigkeiterst wesentlichenlauftdieAbhangigkeitderDispersionsrelationvonderGitterweitehdaraufhinaus, 56 KAPITEL4.TECHNISCHEASPEKTEDERIMPLEMENTATION 

imLimesh!0gegendieAusbreitungsgeschwindigkeitdeskontinuierlichenProblemsgeht.Auch istdieGeschwindigkeitabhangigvonderWellenlangeunddavon,obdieAusbreitunginRichtung desGittersoderdiagonaldazuverlauft.LetzteresistinAbschnitt5.2numerischuntersucht. 

furt

4.5.STEUERUNGDESGITTERS 57 

Gebietverfeinert,dieserBereichbewegtsichaberimmernochzuschnell,weshalbwirimnachsten 

DurchlaufdasgleicheProblemhabenwerden,wennauchspater. 

ImEndeektbenotigtmanmehrereDurchlaufe,bisalleindereinmalverfeinerteBereichmit 

demtatsachlichenOrtderWelleubereinstimmt.DiegleichenProblemetretenauchaufhoheren 

Verfeinerungsstufenauf,wennauchnichtganzsomarkant. 

AnsatzezurLosungdiesesProblemssindeinerseits,gleichaufeinemrelativfeinenGitter 

anzufangenundbeidendarauffolgendenvieleZellenzuvergrobern,andererseitsamAnfangeine 

gewisseAnzahlvonDurchlaufendurchzufuhren,beidenendieVerfeinerungsehrvorsichtiggehandhabtwird,umeinezustarkeVerfeinerungandenOrtenzuverhindern,wodieexakteLosung, 

imGegensatzzurnumerischenLosungaufzugrobenGittern,glattist.BeiProblemenmitkurzenWellenlangenistderersteWegnichtgangbar,beispielsweisewurdedieForderungnachnur10 

GitterpunktenproWellenlangebereitsaufdemerstenGitterbeideminAbschnitt5.3gerechneten 

Beispiel106ZellenproZeitschrittnachsichziehen. 

ImwesentlichenverhindertdiesesProblemdiemehrfacheVerfeinerungvonZellenmitgroem 

FehlerindikatorineinemDurchgang,wieesbeielliptischenundparabolischenProblemendurchfuhrbarist(vgl.[22,19]).EindritterWegistdieVerwendungvonnitenElementenhoherer 

Ordnung,dieeinegeringereDispersionzeigen,vergleiche[1]undAbschnitt5.2. 

4.5.3Orts-Zeit-Adaptivitat 

EineoptimaleStrategiezurGitterverfeinerungwurdenebenderOrtsgitter-auchdieZeitschrittweiteadaptivanpassen.DieseArtderAdaptivitatistausgehendvondeninAbschnitt2.4vorgestelltenKonzeptenleichtmachbarundin[19]furdieWarmeleitungsgleichungauchinderPraxis 

gezeigt;allerdingsistdieBedeutungderZeitschrittweitenadaptionbeiderWellengleichungnicht 

sogrowiebeiderDiusionsgleichung,wofurimwesentlichenzweiGrundeausschlaggebendsind: 

KeineunterschiedlichenZeitskalen:BeiderWellengleichungsinddieZeitskalenimallgemeinenkonstant;insbesonderegibteskeinestationarenZustande,sodasicheinewesentliche 

VergroerungderZeitschrittweitemeistensverbietet. 

KeinInformationsverlust:BeiderWarmeleitungsgleichungunterliegtInformationstarker 

Dampfung,sodaZielfunktionale,diedieLosungamEndzeitpunktauswerten,groeZeitschritteamAnfangzulassen.DabeiderWellengleichungkeinInformationsverlustvorhanden 

ist,verlangteineAuswertungzubeliebigerZeiteinemoglichstexakteRechnungzuallen 

fruherenZeitpunkten. 

AusdengenanntenGrundenerschiendieImplementationzeitschrittadaptiverMethodennicht 

sorelevant.EinwesentlichwichtigererPunktwarejedochderVergleichvonFehlerinformationuber 

verschiedeneZeitschrittehinweg:dieFehlerschatzerlieferneinenIndikatorwertfurjedeRaum-Zeit- 

Zelle;dieEntscheidung,obeineZelleverfeinertbzw.vergrobertwird,ndetjedochimverwendeten 

ProgrammnurdurchVergleichmitdenanderenZellendesgleichenZeitschrittsstatt.Durchdieses 

VerfahrenwerdenauchZellenverfeinert,derenIndikatorwesentlichkleineristalsdieIndikatoren 

vonZellenaufanderenZeitschritten,dienichtverfeinertwerden.ImEndeektvergroertsichso 

dieZahlderfureinegegebeneGenauigkeitbenotigteZahlanFreiheitsgraden;inAbschnitt3.3ist 

einBeispielangefuhrt,wodieEinsparungerheblichware. 

TrotzdemwurdeimRahmendieserArbeitvoneinerImplementationdiesesQuervergleichsAbstandgenommen,daderVergleichvonbiszu50.000.000IndikatoreneineerheblicheprogrammundspeichertechnischeHerausforderungdarstellenwurde.FurzukunftigeArbeitenistdieseOptimierungaberwunschenswertunderfolgversprechend. 

Einweiteres,nichtverfolgtesZielistdieVerwendungortlichunterschiedlicherZeitschrittweiten. 

EbensowiedieOrtszellenlokalverfeinertwerden,sollteesmoglichsein,dieOrts-Zeit-Zellen 

einzelnzuverfeinern.Dieswurdeeserlauben,dieOrts-Zeit-GitternahezuoptimalandasProblem 

anzupassen.NebendemzuerwartendenerheblichenImplementationsaufwandistdieserAnsatz 

allerdingsnurdannmoglich,wennesgelingt,dieverwendeteFormulierunganalogzuAbschnitt2.3 

indieeinzelnen,dannlokalenZeitschrittezuentkoppeln.DieseEntkopplungistjedochschwierig,

sodasichinderLiteraturnurwenigepraxisrelevanteAnsatzezurVerwendungvonRaum-Zeit- 58 ElementenndenundauchdiesevorwiegendnurfureineRaumdimension(fureinsolchesBeispiel KAPITEL4.TECHNISCHEASPEKTEDERIMPLEMENTATION 

vergleiche[16]).

Kapitel5 

WeiterenumerischeBeispiele 

adaptivenMethodengegenuberglobalerVerfeinerungzuergrunden.DiemeistenderBeispielehabenkeinedirekteAnwendung,dienenaberprototypischalsreduzierteFallerealerProbleme.Dazu 

Punkt-undLinienauswertungenuberdieZeitintegriertundeinRaum-Zeit-Integral.Zusammen IndiesemKapitelsolleneinigeweitereBeispieleuntersuchtwerden,umVor-undNachteileder 

mitdenGebietsintegralendesletztenKapitelssindsomitauerPunkt-undLinienauswertungen allgemeinenkeinwohldeniertesFunktionalaufdemLosungsraum. ohneZeitintegralalleTypenvonFunktionalenabgedeckt;diePunktauswertungistallerdingsim wurdenZielfunktionaleausgewahlt,umeinSpektrummoglicherAnwendungabzudecken,darunter 

veranderlichenundnurandieKoezientenadaptiertenGittern. wirdgezeigt,dadiedamitzusammenhangendenProblememitetwasSorgfaltumgangenwerden konnenunddannzuwesentlichbesserenErgebnissenfuhrenalsbeiVerwendungvonzeitlichnicht oftkritisiertwird,namentlichdieteilweiseReexionvonWellenanGitterdiskontinuitaten.Es AlsletztesBeispielwirdeinEektuntersucht,derbeiderVerwendungadaptiverGitterzurecht 

denzellweisenIndikatorenbestimmtwird,welcheZellenverfeinertodervergrobertwerdensollen, vonEinstellmoglichkeitenabhangt;dazuzahlenvorallemdasStartgitter,dieStrategie,mitderaus miertwurden,vorallemaberdadieRechenzeitbeidenadaptivenRechnungenvoneinerVielzahl WertekonnennureinegrobeRichtschnursein,dadieProgrammenichtaufGeschwindigkeitopti- 

IneinigenderfolgendenAbschnittenistderFehlergegendieRechenzeitaufgetragen.Diese 

dadurchausgiebigesSpielenmitdiesenWerteneinmehrfachgeringererRechenaufwandmoglich ist,wasbeidenRechnungenmitglobalverfeinertenGitternnaturgemawegfallt.Eswurdetrotzdemdaraufverzichtet,hierOptimierungenvorzunehmen,daesmehrumdieDemonstrationder 

undschlielichdieAnzahlderzuverfeinerndenodervergroberndenZellen.DieErfahrungzeigt, 

Rechenzeitangegebenist,inklusivedervorherigenDurchlaufe,diezurVerfeinerungdesGitters benotigtwurden;diesesindbeiglobalerVerfeinerungnaturlichnichtnotigunddaherauchnicht Konzepteging;OptimierungderLaufzeitkannnurbeiechtenBeispielenausderPraxissinnvoll sein.BeiderAngabederRechenzeitistzubeachten,dabeiadaptivenRechnungendiegesamte angegeben. Verfeinerungsind,wenndieRechenzeitfurdasletzteGitterunterderHalftederRechenzeit langist,wiefurdenvorherigen.Darausfolgt,daadaptiveVerfahrendanneektiveralsglobale aufeinemglobalverfeinertenGitterliegt.DiesistfureinenEnergiefehlerschatzergegeben,falls erkumuliertwenigeralsetwadieHalftederFreiheitsgradebenotigt;furdendualenSchatzer DieErfahrungzeigt,dadieRechenzeitfurjedenVerfeinerungsdurchlaufungefahrdoppeltso 

istderAufwandzurLosungdesdualenProblemsmitzuberucksichtigen,dienotigeErsparnisan Freiheitsgradenlatsichdahernichtsoeinfachangeben. den,wennmanvonderdann(beikonstanterZeitschrittweite)konstantenSystemmatrixamAn- 

fangeineLU-oderahnlicheZerlegungmachenwurde,dainjedemZeitschrittdannnurnoch einVorwarts-Ruckwarts-Einsetzennotigware.OftistjedochderbegrenzendeFaktorbeiRechnungenmithoherGenauigkeitderverfugbareHauptspeicher,wasdiebeschriebeneTechnikals 

AndererseitskonntedieRechenzeitfurdasglobalverfeinerteGitterwesentlichreduziertwer- 

59

60 KAPITEL5.WEITERENUMERISCHEBEISPIELE 

nichtpraktikabelerscheinenlatunddieReduktionderZahlderFreiheitsgradealswichtigerals 

dieVerringerungderRechenzeiterscheinenlat.TypischerweiseistderBedarfetwa1000-1200 

ByteproFreiheitsgradbeilinearenElementen,sodaderSpeicherausbauderfurdieseArbeit 

zuganglichenRechnereinMaximumbeietwa300.000-500.000FreiheitsgradenproZeitschrittfur 

jedederbeidenVariablensetzt;RechnungendauernbeidieserZahlanFreiheitsgradenund200 

ZeitschritteneinbiszweiTage,wassichbeimEinsatzvonMehrgittertechnikendeutlichverringern 

lassensollte. 

5.1 ZeitintegraleinerPunktauswertung 

BeiderSimulationseismischerWellenistdieAuswertungderVerschiebungoderderGeschwindigkeitaneinemPunkt(z.B.aneinerErdbebenstation,ummitMedatenvergleichenzukonnen) 

einhaugerFall.IndiesemAbschnittseienadaptiveundnicht-adaptiveVerfahreneinandergegenubergestellt,umdieGenauigkeitvergleichenzukonnen. 

ZulosenseidieWellengleichungmitkonstantenKoezientena1aufdemGebiet 

[?1;1]2.useiaufdemRandNullunddieAnfangswerteseiendurcheineradialsymmetrische 

Funktiongegeben: 

u0(r)=0; 

v0(r)=(s?r); 

mits=1 

10undderHeavisideschenSprungfunktion.SolangedieWelledenRandnichterreicht, 

d.h.furt

0.1 

0.09 

0.08 

0.005,d.h.eswurden100Zeitschrittedurchgefuhrt. 

u(0,t) 

0.1 

0.09 

0.08 

2 Verfeinerungen, Energieschaetzer 

6 Verfeinerungen, Energieschaetzer 

Exakt 

0.07 

0.07 

Auslenkung u 

0.06 

0.05 

0.04 

Auslenkung u 

0.06 

0.05 

0.04 

0.03 

0.03 

0.02 

0.02 

0.01 

0.01 

0 

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 

Zeit 

0 

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 

Zeit 

0.1 

0.09 

0.08 

2 Verfeinerungen, Dualer Schaetzer 

6 Verfeinerungen, Dualer Schaetzer 

Exakt 

0.1 

0.09 

0.08 



Exakt 

0.07 

Abbildung5.1:ZeitlicherVerlaufderAuslenkungu(0;t)amUrsprunginderexaktenLosung 

0.07 

Auslenkung u 

DiesesIntegrallatsichleichtauswertenundmanerhalt 5.1.ZEITINTEGRALEINERPUNKTAUSWERTUNG 61 

DerexakteWertdesobigenFunktionalsistdamit18?120p6+1 sprungistinAbbildung5.1dargestellt.DienumerischenErgebnissesindnachzweiundnach DerzeitlicheVerlaufderkontinuierlichensowiederVerlaufdernumerischenLosungimUr- 

u(0;t)=t?(t?s)pt2?s2: 200ln(5+2p6)0:013988. (5.1) 

sechsVerfeinerungszyklendargestellt,obenrechtsfurVerfeinerungmiteinemEnergiefehlerindikator,untenlinksmitdemdemProblemangepatendualenFehlerschatzerunduntenrechtsbei 

globalerVerfeinerungaufkonstant1024undauf16384Zellen,d.h.mit4225bzw.66049FreiheitsgradenproZeitschritt.DieRechnungwurdemitbiquadratischenElementenfurdasprimaleund 

bikubischenElementenfurdasdualeProblemdurchgefuhrt.DieZeitschrittweitebetrugkonstant 

0.06 

0.06 

0.05 

0.05 

(linksoben)sowiedernumerischenLosungnachzweiundnachfunfbzw.sechsVerfeinerungszyklen.RechtsobenVerfeinerungmiteinemEnergiefehlerindikator,linksuntenmitdemangepaten 

0.04 

0.04 

0.03 

0.03 

0.02 

0.02 

dualenProblem,rechtsuntenbeiglobalerVerfeinerung. 

0.01 

0.01 

0 

0 

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 

Zeit 

Zeit 

identisch,daaufdemgleichenGrobgittergerechnetwurde;daderdritteWertsoniedrigliegt,ist derFreiheitsgrade1undgegendieRechenzeitfurdieverschiedenenFehlerschatzerundglobale ZahlenindeneinzelnenZeitschrittengewahlt.DerersteWertistbeiallendreiKurvenjeweils Verfeinerunggegeneinanderaufgetragen.AlsAnzahlderFreiheitsgradewurdedieSummeder InAbbildung5.2sinddierelativenFehlerbeiderAuswertungdesFunktionalsgegendieAnzahl 

Darstellungnichtzusehenist.DadieAuswertungderFehleridentitat(2.22)durchRechnendes Zufall,daderFehlerindiesemBereichseinVorzeichenwechselt,wasaberinderlogarithmischen 

FreiheitsgradeinderGeschwindigkeitv,soerhaltmandendoppeltenWert. wurdenurdieAnzahlderFreiheitsgradefurdieursprunglicheVariableuakkumuliert,berucksichtigtmanauchdie dieZahlzwischeneinzelnenZeitschrittenstarkschwankenkann,istdiesdieeinzigevergleichbareGroe.Allerdings 1WieinKapitel3istdieAnzahlderFreiheitsgradeuberdieeinzelnenZeitschritteaufsummiertangegeben;da 

Auslenkung u

62 dualenProblemsmitumeinserhohtemPolynomgraderfolgte,istderVorteildesdualenSchatzers gegenuberdemEnergiefehlerindikatorbeiderRechenzeitnichtsodeutlich;dasVerhaltnissollte KAPITEL5.WEITERENUMERISCHEBEISPIELE 

aberklarersein,wennmanmitdemgleichenAnsatzgradrechnet(Abschnitt2.4.4),dadannder 

1 

AufwandfurdasdualeProblemnichtmehrdenfurdasprimaleProblemuberwiegt. 

Energieschaetzer 

Dualer Schaetzer 

Globale Verfeinerung 

1 




0.1 

0.1 

Abbildung5.2:RelativerFehlerinAbhangigkeitvonderZahlderFreiheitsgradeundderRechenzeit 

0.01 

0.01 

0.001 

0.001 

0.0001 

0.0001 

vomexaktenVerlauf,sonderndiemittlerequadratischeAbweichung beiverschiedenenVerfeinerungsverfahren. ImallgemeineninteressiertnichtdasZeitintegraluberu(0;t),d.h.diemittlereAbweichung 

10000 100000 1e+06 1e+07 

10 100 1000 10000 100000 

Anzahl an Freiheitsgraden 

Rechenzeit Sekunden 

rms=ZIju(0;t)?uh(0;t)j212: 

Relativer Fehler 

DieserFehleristinAbbildung5.3furdieverschiedenenVerfeinerungskriteriendargestellt. 

Relativer Fehler 

0.1 




0.1 




Mittlerer quadratischer Fehler 

Mittlerer quadratischer Fehler 

Abbildung5.3:MittlererquadratischerFehlerrmsinAbhangigkeitvonderZahlderFreiheitsgrade 

0.01 

0.01 

SchatzerverfeinertenGitterssindbesseralsdiederanderenVerfahren,obwohldesFehlerfunktionalnichtandieFragestellungangepatwar. 

undderRechenzeitbeiverschiedenenVerfeinerungsverfahren.DieErgebnissedesmitdemdualen 

0.001 

0.001 

10000 100000 1e+06 1e+07 

10 100 1000 10000 100000 

Anzahl an Freiheitsgraden 

Sekunden 

diesenBereichmitdeutlichwenigerZellenalsdieanderenbeidenProzessezuerreichen.Der drittletzte,sehrniedrigeWertdesdualenSchatzersinAbbildung5.2istallerdingseherzufalliger Abbildung5.3)liegt.DasdurchdendualenFehlerschatzergesteuerteVerfahrenistinderLage, verandertwurde,beietwa0.5-1Prozent(Zeitintegral,Abbildung5.2)bzw.0.002-0.003(rms, AusdenAbbildungengehthervor,daderFehlerdurchdieZeitdiskretisierung,dienicht 

Natur;dortwechseltederFehlerseinVorzeichen. InAbbildung5.4sinddievomdualenSchatzerundvomEnergiefehlerindikatorerzeugtenGitter

5.1.ZEITINTEGRALEINERPUNKTAUSWERTUNG 63 

t=0 t=16 t=13 t=12 

undvomEnergiefehlerindikator(unten,nachsechsVerfeinerungsschritten)erzeugtenGitterund Abbildung5.4:VergleichdervomdualenSchatzer(oben,nachsiebenVerfeinerungsschritten) Losungenvh.

64 KAPITEL5.WEITERENUMERISCHEBEISPIELE 

einandergegenubergestellt.Esistdeutlichzuerkennen,daderdualeSchatzernurdortverfeinert, 

woesfurdasEndergebniswichtigist,wahrenddieWelleselbstnursehrschlechtaufgelostwird. 

5.2 WinkelabhangigkeitderAusbreitungsgeschwindigkeit 

Esistbekannt,dadieAusbreitungsgeschwindigkeitabhangigdavonist,obdieWelleinRichtung 

derGitterlinienoderdiagonaldazulauft(siehez.B.[1]).ImallgemeinenwirddieserEektals 

"winkelabhangigeAusbreitungsgeschwindigkeit\bezeichnet,wobeimitdemWinkelderWinkel 

zwischenAusbreitungsrichtungunddenGitterliniengemeintist. 

DerbeschriebeneEektistbesondersdastorend,wodiegenaueAnkunftszeiteinerWelleeine 

Rollespielt,beispielsweisebeimVergleichvonsimuliertenErdbebenwellenmitdenAufzeichnungen 

vonMestationen.DieAbweichungderDispersionsrelationvomrichtigenVerlaufistfurViereckselementeinetwa2-5malkleineralsbeiDreiecken(vgl.[21]);derEektderwinkelabhangigen 

AusbreitungsgeschwindigkeitenistfurlineareElementebesondersausgepragtundsollindiesem 

Abschnittuntersuchtwerden.DasBeispielselbstistvonkeinempraktischenWert. 

ZulosenistwiederdiehomogeneWellengleichungmitkonstantemKoezienten.AlsAnfangsverteilungwurdeu0=(a?r)e?(ra)21?r2 

a2;v0=0mita=110gewahlt.DieexakteLosungist 

wiederradialsymmetrisch. 

AlsZielfunktionalwurde 

J(u)= ZT 

0Zu(r;;t)!(r;)?!r;+4drd2dt!12 

=k(u;w)kL2([0;T]) 

gewahlt.DieGewichtsfunktionsei 

!(r;)=max(cos4;0)r?34 

a; (s)=(1?s2)(1?jsj); 

w=!(r;)?!r;+4; 

mita=0:03.DieGewichtsfunktionwistinAbbildung5.5dargestellt.Sieistsogewahlt,dasiedie 

TeilederWelle,dieparallelzuGitterlinienunddiediediagonaldazulaufenmitunterschiedlichen 

Vorzeichengewichtet.AufdieseWeiseerhaltmangenaudieDierenzzwischendenTeilender 

WelleparallelunddiagonalzumGitter;furdieexakteLosungsinddiebeidenTeilegleichundder 

WertdesFunktionalsistNull.AlsReferenzfurdieGroenordnungderzuerwartendenErgebnisse 

kanndernumerischgewonneneWertk(u;jwj)kL2([0;T])3:2210?3angesehenwerden,derdie 

beidenTeilemitdemgleichenVorzeichengewichtet. 

FurdendualenFehlerschatzermuwiedereinlinearisiertesFunktional~J(uh;)gewahltwerden, 

soda~J(uh;e)=J(u)2?J(uh)2;daderersteSummandverschwindet,istdieGleichheittrotz 

derNichtlinearitathiererfullbarundmanwahlt 

J(uh;')=~J(uh;')=ZT 

0(w;uh)(w;')dt: 

DerFaktor(w;uh)inJgewichtetdieZeitenhoher,beideneneineAbweichungvonderSymmetrie 

vorliegt.DerFehlerJ(u)?J(uh)=?J(uh)=?pJ(uh)2=?p?J(u)2+J(uh)2wirddurch 

?p?J(uh;e)geschatzt.DasFunktionalJstimmtmitdemexaktenFunktional(2.27)uberein, 

wahrenddasnach(2.28)linearisierteFunktionalgenaudendoppeltenWerthatte. 

InAbbildung5.6sinddieFehlerJ(uh)furverschiedeneVerfeinerungsstrategiendargestellt. 

EristsowohlfurglobaleVerfeinerungalsauchfurVerfeinerungmitdemEnergiefehlerschatzer 

proportionalzuN?1,wobeiNdieaufsummierteAnzahlanFreiheitsgradenderursprunglichen 

VariableudesprimalenProblemsist.DieserVerlaufkorrespondiertungefahrmiteinerKonvergenz 

proportionalzuh?2.

5.2.WINKELABHANGIGKEITDERAUSBREITUNGSGESCHWINDIGKEIT 65 

1 

0.8 

0.6 

0.4 

0.2 

gesetzt. Abbildung5.5:DieGewichtsfunktionw.DerbesserenDarstellbarkeithalberwurdehiera=0:06 

0 

-0.2 

-0.4 

-0.6 

-0.8 

-1 

0.01 

0.001 




Energieschaetzer, kubische Elemente 

0.01 

0.001 




Energieschaetzer, kubische Elemente 

0.0001 

0.0001 

verschiedenenVerfeinerungsverfahren.ManvergleichedieWertemitdemimTextangegebenen Referenzwert3:2210?3. Abbildung5.6:FehlerinAbhangigkeitvonderZahlderFreiheitsgradeundderRechenzeitbei 

1e-05 

1e-05 

1e-06 

1e-06 

1000 10000 100000 1e+06 1e+07 1e+08 

1 10 100 1000 10000 100000 

Anzahl Freiheitsgraden 

in Sekunden 

zeigendasnach[1]erwarteteVerhalten,dadergleicheFehlerbeiwenigeralsderHalfteder FreiheitsgradeundetwaderHalftederRechenzeiterreichtwird. ZumVergleichistauchderFehlerbeiVerwendungvonkubischenElementendargestellt.Sie 

letztendreiPunkteindoppeltlogarithmischerAuftragungpraktischkollinearundmanndeteineKonvergenzratevonN?1:05furdenechtenFehlerJ(uh)undvonN?0:95furdenSchatzer 

InAbbildung5.7sinddieWertefurFehlerschatzerundtatsachlichenFehlerangegeben,wobeidieVerfeinerungmitdemdualenSchatzerdurchgefuhrtwurde.InbeidenReihenliegenditionalemussenimallgemeinenlinearisiertwerden,wobeidieLinearisierungtheoretischumdie 

(?J(uh;e))12. 

exakteLosunguvonvornhereinunmoglich,dadiefunktionaleAbleitungandieserStelleNull exakteLosungstattndensollte,inErmangelungderKenntnisdavonaberumdienumerische Losunguhgemachtwird.ImindiesemAbschnittbehandeltenFallistdieLinearisierungumdie AufgrundderKonstruktionvonJistdieserFalletwaspathologisch:nichtlineareZielfunk- 

istunddieLinearisierungistsobeschaen,daJ(uh;uh)=J(e;uh)=J(uh;e)=J(e;e).Da e!0,konvergiertauchJgegenNullunddamitauchdiedualeLosungw.DiedualeLosungist verringertwird;siekannnichtverhindern,daderFehleranandererStelleneuentsteht.Esist somitsobeschaen,dasiedasGittersosteuert,daderFehlerdesletztenVerfeinerungszyklus' zeigtedieArbeitandiesemBeispiel,dadieKonvergenzsehrsensitivvonderWahlderVerfeinerungsparameterabhangt;ineinigenFallenverfeinertedasVerfahrenzwaraneinigenStellen, 

erstaunlich,dadasGittertrotzdemgegeneinevernunftigeKongurationkonvergiert.Allerdings 

rms 

rms

66 N J(uh) p?J(uh;e)Verhaltnis KAPITEL5.WEITERENUMERISCHEBEISPIELE 

99.412 81.205 6:1510?4 3:2810?4 7:6410?4 2:1310?4 1:24 

1.245.9832:0310?5 189.129 293.614 535.133 1:7310?4 1:3510?4 4:8010?5 1:9410?4 2:8710?4 1:2710?4 5:6110?5 0:65 1:12 2:12 2:65 

Abbildung5.7:VergleichzwischenechtemundgeschatztemFehler.ManvergleichedieWertemit 3.134.6727:4210?6 2:3710?5 2:76 

demimTextangegebenenReferenzwert3:2210?3. 3:19 

vernachlassigteaberandere,aufdenenderFehlerimnachstenDurchlaufbeinahegenausogro 

1e-06 

warwieimaktuellen;dieVerfeinerung"liefdemFehlerimmerhinterher\. ist,dasdualeProblemnurbiszueinerGitterverfeinerungsstufemitzurechnen,beidersichdieGewichte!iK;nausAbschnitt2.4.4,alskontinuierlicheFunktionaufgefat,2nichtmehrwesentlich 

reduzieren;eswaredannnurnochnotig,dasdualeProblemaufeinemgrobenGitterzuberechnen andern.DieserVorschlagwurdegemacht,umdenAufwandzurBerechnungdesFehlerschatzerszu Esistnochanzumerken,daoensichtlichbeidiesemZielfunktionaldieVariantenichtmoglich 

Fall,dadiedualeLosungnurdieGenauigkeitderprimalenLosungwiderspiegelt. RechnungdesprimalenProblemsnichtmehrwesentlichandert;diesisthierabergeradenichtder unddieGewichteabzuspeichern.DieserAnsatzistprinzipiellauchbeinichtlinearenZielfunktionalenanwendbar,wenndavonausgegangenwerdenkann,dasichdiedualeLosungbeigenauerer 

5.3 gerechnet,dervieleDiskontinuitatenenthalt: AlsBeispielmitvariablenKoezientenwurdedieWellengleichungmiteinemKoezientena(x) StreuunganvielenDiskontinuitaten 

a(x)=1+12t(x)+t2x+y t(s)=1wennsin(3s)>0; 0sonst. p3; 

DerKoezientistinAbbildung5.8dargestellt.KoezientendieserArttreteninderGeologiebei starkgefaltetenGesteinsschichtenauf;allerdingsistdieVariationdesKoezientenimallgemeinen soverteilt,dasienichtalleaufGitterlinienundauchnichtparalleloderdiagonaldazuliegen. weitkleineralsindiesemBeispiel,dafurgibtesmehrUnstetigkeiten.DieDiskontinuitatensind ungen,uberallsonsthomogeneDirichlet-Bedingungengesetzt;letzteresistnichtrealistisch,da eigentlichabsorbierendeRandbedingungengesetztwerdenmuten.DieAnfangswertewurdeauf DasGebietistwieder[?1;1]2,alsRandwertewurdenobenhomogeneNeumann-Randbeding- 

u0=0; 

mits=0:02gesetzt.DieSimulationszeitwurderelativgrozuT=2gewahltundeswurden300 v0=(s?r)e?jxj2 s21?jxj2 

Zeitschrittedurchgefuhrt. s2; 

licheFunktionkonvergieren. 2DieSkalierungderGewichteinAbschnitt2.4.4wurdejageradesodurchgefuhrt,dasiegegeneinekontinuier- 

Fehler 

0.001 

0.0001 

1e-05 

Echter Fehler 

Geschaetzter Fehler 

1000 10000 100000 1e+06 1e+07 

Freiheitsgrade

5.3.STREUUNGANVIELENDISKONTINUITATEN 67 

2 

1.5 

1 

Abbildung5.8:StrukturdesKoezientenmitvielenDiskontinuitaten. 

0.5 

0 

1 

0.5 

x 

0 

Abbildung5.9:SynthetischesSeismogrammderWellenausbreitung,amoberenRanddesGebietes abgenommen. 

-0.5 

-1 

0 0.5 1 1.5 2 2.5 

brachtenakustischenSignalsauf,soistmandaraninteressiert,dieSimulationwh(x;t)mitden FatmandasBeispielalsdieAusbreitungeinerErdbebenwelleodereinesabsichtlicheinge- 

Zeit 

Mewertenw(x;t)anderOberachey=1zuvergleichen.InAbbildung5.3istdaszugehorige, aufgetragen.DeutlichistdiehyperbolischeKurveerkennbar,diedasersteAuftreenderWelleauf renGrenzedesGebietszueinembestimmtenZeitpunktdarstellt;dieAuslenkungistnachrechts denoberenRandkennzeichnet,sowiediegekreuztenLinien,diedieVerlangerungenderHyperbel sindundvondenamrechtenundlinkenRandreektiertenTeilenderWellestammen,diean sogenannte"synthetischeSeismogramm\,indemjedevertikaleLiniedieAuslenkunguanderobe- 

denoberenRandkommen.EbenfallszusehensinddieteilweisevorhandenenReexionenunddie nochausdemUrsprungstammendenNachwellenderAnfangsverteilung,sowiedieStorungender FormendurchdievariablenKoezienten. 

DadieexakteLosungabernichtbekanntist,istdieAuswertungdiesesFunktionalsnichtmoglich. DieindiesemBeispielzukontrollierendeGroewareeigentlich 

richtigwiedergibtundlinearist,umesverhaltnismaigleichtauswertenzukonnen.DerMittelwert WirwahlendahereinFunktional,daswenigstensdieOrtsabhangigkeitderinteressierendenGroen J(e)=kw(x;t)?wh(x;t)k(\fy=1g)I:

68 derFunktion J(w)=ZT KAPITEL5.WEITERENUMERISCHEBEISPIELE 

istdafurallerdingsnichtgutgeeignet,daunterschiedlicheAnkunftszeitenund-orteeinzelner WellenkeinenUnterschiedimErgebnismachen.Daskannmanallerdingserreichen,indemman 0Zu(x;y=1;t)dxdt 

EinzeitlichleichtverschobenesSignalfuhrtaufgrunddesdannanderenGewichtsfaktorszueinem miteinemstarkoszillierendenGewichtsfaktorwahlt,beispielsweise!(x;t)=sin(3x)sin?5tT. J(w)=ZT 0Zu(x;y=1;t)!(x;t)dxdt 

pischeZeit(RadiusderAnfangsverteilungdurchmittlereAusbreitungsgeschwindigkeit)gewahlt, deutlichanderenErgebnisJ.DiezeitlicheOszillationistsogewahlt,dadiePeriodedeutlich vitatgegenVerschiebungeninderGroenordnungbeispielsweiseeinerhalbenPeriodederWellen groeralsdiePeriodederWellenist,andererseitsaberauchwiedernichtsogro,dadieSensiti- 

verlorenginge.DiezeitlichePeriodederGewichtsfunktionwurdehier30malsogrowieeinety- 

dieortlichePeriodeebenfalls30malsogrowieeinetypischeLange(hierderRadiusderAnfangsverteilung)stendreiWertepaarevondualemFehlerschatzerundEnergiefehlerindikatorsindidentisch,dadie 

DurchExtrapolationderWertebekommtmaneineSchatzungdesexaktenWertesdesZielfunktio- 

VerfeinerungindiesenDurchlaufenjeweilsnachdemEnergiefehlerindikatordurchgefuhrtwurde. DieErgebnissederRechnungsindindenAbbildungen5.10und5.11dargestellt.Inderersten AbbildungistderVerlaufvonJ(wh)gegendieAnzahlanGitterzellenwidergegeben.Dieernals;durchVergleichmitdiesemWerterkenntman,dadieRechnungmitdemdualenProblem 

inderLageist,dasFunktionalmitdeutlichgeringererZellzahlgutzuapproximieren. LokalisierungdesEinugebieteszuberucksichtigen,indemnurderBereichvonverfeinertwird, vondemausuberhauptBeitragezuJ()gelangenkonnen;insbesonderewerdengegenEndeder RechnungwesentlichwenigerZellenbenotigtalsbeimEnergiefehlerindikator,derversucht,allen GitterundLosungengezeigt.Manerkenntdeutlich,daderdualeSchatzerinderLageist,die InderzweitenGraksinddievomEnergiefehlerindikatorunddemdualenSchatzererzeugten 

WellenundReexionenzufolgen.DasvomdualenSchatzerzumZeitpunktt=0erzeugteGitter derprimalenauchandiedualeLosunganzupassen(vgl.Abschnitt4.5.1). iststarkerverfeinertalsdasdesEnergiefehlerindikators,dadortversuchtwird,dasGitterneben 

2:403:759?4:28610?6 NDualerSchatzer J(wh) 1:918:696?4:17710?6 327:789 920:380 ?2:98510?6 ?4:63010?6 2:403:759?4:28610?6 5:640:223?4:38510?6 327:789 920:380 N ?2:98510?6 ?4:63010?6 J(wh) 

2:975:119?4:43810?610:189:837?4:46310?6 

Abbildung5.10:VergleichdermitdemdualenSchatzerunddemEnergiefehlerindikatorerhaltenen 6:203:497?4:52410?617:912:981?4:52110?6 

ErgebnisseJ(wh)inAbhangigkeitvonderbenotigtenZellzahl.DurchExtrapolationbekommtman 41:991:779?4:51710?6 

alswahrscheinlichstenWertJ(w)=?4:51510?6:::?4:52010?6. 

DieteilweiseReexion(spuriousreection)vonWellenanGitterdiskontinuitatenisteininder 5.4 LiteraturvielfachbeschriebenesundalsgroesHindernisfurdieVerwendungadaptiverMethoden TeilweiseReexionanGitterunstetigkeiten

5.4.TEILWEISEREFLEXIONANGITTERUNSTETIGKEITEN 69 

t=0 t=23 t=43 t=2 

linksuntenv0dargestellt. Abbildung5.11:VomdualenSchatzer(oben)undvomEnergiefehlerindikator(unten)erzeugten GitterundLosungenuzuverschiedenenZeitpunkten.DazumAnfangszeitpunktu0=0ist,ist

Abbildung5.12:FestesGittermitDiskontinuitaten(links)undtypischesGitterbeiderVerwendung 

1 

1 

adaptiverVerfahren(rechts). 

0 

0 

0 1 2 3 0 1 2 3 

0.08 

0.06 

u(x=y=0.5,t) 

0.08 

0.06 

u(x=y=0.5,t) 

0.04 

0.04 

0.02 

0.02 

Abbildung5.13:VergleichderSignaleu(x=0:5;y=0:5;t)beifestemGitter(links)undbei 

70 erkanntesProblem.Umeszuuntersuchen,wurdenRechnungenderWellengleichungmitkonstantenKoezientena==1aufdemGebiet(0;3)(0;1)durchgefuhrt;obenunduntenwurden 

KAPITEL5.WEITERENUMERISCHEBEISPIELE 

homogeneNeumann-Randwerte,linksundrechtsDirichlet-Randwertevorgeschrieben,wobei dieRandfunktionlinkszugD(x=0;y;t)=sin2(5t)furt0:7dargestellt. UmdieReexiondervonlinksgegendieGitterunstetigkeitenlaufendenWellenzuverdeutli- 

1 1.5 2 2.5 3 

1 1.5 2 2.5 3 

t 

t 

DieexakteLosungistandiesemPunktfurt>0:7identischNull,dadieeinlaufendeWelleeine halbeZeiteinheitbiszudiesemPunktbenotigtunddenPunktdemnachaucheinehalbeZeiteinheitnachdemEndederInjektionvomlinkenRandpassierthat.Stattdessenbeobachtetmanam 

AnfangnochdieNachlauferderWelle,diehierabernichtinteressieren,sowiezwischent=1:5und Unstetigkeit;abt=2:5istauerdemdieamlinkenRandreektierteersteReexionwiederam 1:7dieReexionderWelleandererstenUnstetigkeitundabt=2dieReexionanderzweiten Auswertungspunkt.DiezeitlicheLangederzweitenReexionistwesentlichgroeralsdieDauer

gnalnachPassierendererstenundvorErreichenderzweitenGitterunstetigkeitbereitseineLange derursprunglichenWellevon0:2Zeiteinheiten;dieseVerlangerungruhrtdaher,dadasHauptsi- 

5.4.TEILWEISEREFLEXIONANGITTERUNSTETIGKEITEN 71 

diederzweitenetwa6ProzentderAmplitudederursprunglichenWellen.Insgesamttrittbeider auchReexionmiteinernichtvernachlassigbarenAmplitudeauf. vonrund0:3,nachPassierenderzweitenDiskontinuitatsogarvonrund0:7Zeiteinheiten(jeweils ohnediekleinenNachlaufer)hat.DieAmplitudedererstenReexionbetragtrund0:9Prozent, VerwendungdieserfestenGittersalsonebenderstarkenAnderungderFormderprimarenWelle bildungen5.12und5.13jeweilsrechtsdargestellt.DermaximaleVerfeinerungsgradwurdeso begrenzt,dakeineZellekleineralsdiekleinsteZelledesfestenGitterswar;insgesamthattediese Rechnungaufsummiert209.296FreiheitsgradeinderVariableu(unddamitdoppeltsovieleinsgesamt),wahrenddieRechnungaufdemfestenGitter958.245benotigte.Esistoensichtlich,da 

DieErgebnissemitVerfeinerungdurcheinenEnergiefehlerindikatorsinddagegenindenAb- 

treensollte. jageradesogewahltwar,daesderWellefolgtunddiesedahernieeinegroereUnstetigkeit dieReexionanGitterunstetigkeitenkeineRollespielt,wasauchnichtuberrascht,dadasGitter 

KapitelngegebenenBeispielezeigen,daesdabeinormalist,daeinigeWellennichtaufgelost lenSchatzerszurGitterverfeinerungpassiert.BeidiesemwirddasGitternichtausschlielichnach derLosung,sondernauchnachderZielgroegesteuert,unddieindenletztenAbschnittenund werdenundalsoirgendwannineinGebietmitgroberemGitterlaufen.DabeisolltenauchRe- EinesichindiesemZusammenhangjedochergebendeFrageist,wasbeiVerwendungdesdua- 

exionenentstehen,dieindasEinugebietdesZielfunktionalszurucklaufenunddasErgebnis derRechnungverfalschen.Mankonntediesvergleichenmitdererrorpollutionbeielliptischen Dierentialgleichungen,beiderauchaufgrundnichtoptimalangepaterGitterFehlerweitabvom ten.DerFehlerkannhiersowohlortlichalsauchzeitlichweitabvonderStelleauftreten,wodas UrsprungsortdesProblems,beispielsweiseeinerSingularitataneinereinspringendenEcke,auftre- 

Gitternichtoptimalwar. teilweiseReexionzu"sehen\unddasGitterentsprechendzuverandern.Imallgemeinenistdas zweifelhaftundesscheintnichtausgeschlossen,daderdualeSchatzerdieseArtvonFehlernnur Arbeitabernichtmehrdurchgefuhrtwerdenkonnten. schlechtunterdruckenkann;hiersindweitereUntersuchungennotwendig,dieimRahmendieser Esistnunfraglich,obderdualeSchatzerinderLageist,dieBeeinussungderZielgroedurch

72 KAPITEL5.WEITERENUMERISCHEBEISPIELE

AnhangA 

AprioriFehlerschrankenfur einigeZeitschrittverfahren 

IndiesemAbschnittsolleneinigeaprioriAbschatzungenderZeitdiskretisierungdesverwendeten Systems vt?u=0; u(x;0)=u0; v(x;0)=v0 ut?v=0; (A.2) (A.1) 

gegebenwerden.DerEinfachheithalberwerdendieKoezientenalskonstantangenommen. AbschatzungendesL1-Fehlerszuerhalten;derdurchdieOrtsdiskretisierungverursachteFehler DaruberhinauswirdnurderEektderZeitdiskretisierungbetrachtet,waseserlaubt,scharfe wirdnichteinbezogen. schranktesGebietdurchgefuhrt,umdieFormelnubersichtlichzuhalten.DieErweiterungauf mehrereRaumdimensionenistleichtdurchfuhrbar,indemmandieentsprechendenGreenschen spielsweise[9]).DieEinschrankungaufeinbeschranktesGebietistnurfurPunktedesGebiets Funktionenverwendet;diesesindauchfurzweiundmehrRaumdimensionenbekannt(vgl.bei- 

DieRechnungensindnurfureineRaum-undeineZeitdimension,sowieeinortlichunbe- 

reektierende(d.h.Dirichlet-oderNeumann-)Randbedingungenverwendetwerden. digkeitist;mankannsichleichtuberlegen,dadieMehrzahlderErgebnissegultigbleibt,falls relevant,derenAbstandzumRandkleineralsdieZeitschrittweitemalderAusbreitungsgeschwin- 

WirbetrachtendieexakteLosungderWellengleichungzumZeitpunktt=k,d.h.nachdemersten A.1 d'AlambertschenFormeldurch Zeitschritt,diewirmitdersemidiskretisiertenLosungvergleichenwerden.Erstereistgemader Vorbemerkungen 

u(x;t=k)=12(u0(x?k)+u0(x+k))+12Zk =Z1 +Z1 ?1dy12((y?k)+(y+k))u0(x?y) ?kdyv0(x?y) 

gegeben.SielatsichalsoangebenalsFaltungderAnfangswertemitIntegralkernen.Ausdem VergleichderexaktenIntegralkernemitdenbeiderDiskretisierungentstehendenwerdenwir ?1dy12(k?jyj)v0(x?y) (A.3) 

73

versuchen,dieGuteeinesVerfahrensabzuschatzen.DerVergleichwirdjeweilsfurdenersten Zeitschrittdurchgefuhrtwerden,unddawirnurdieSemidiskretisierungbetrachtenwerden,sind 74 ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN 

u0undu0synonym. Lemma1Esgilt FurdiefolgendeAnalysebenotigenwirnochzweiLemmata: 

wobeidasFaltungsprodukt(!)(x)=R(y)!(x?y)dybezeichneund~und~!dieFourier- Transformiertenvonund!sind. k(!)(x)k2L2(x)=2?j~(p)j2;j~!(p)j2L2(p); 

Beweis:Zuerstzeigenwir,dadasFaltungsproduktimFourier-RaumdemnormalenProdukt entspricht:F[(!)(x)](p)=Zdx1 =Zdx1 p2eipxZdy(y)!(x?y) 

Zdq1 p2eipxZdy 

p23ZdqZdrZdxei(p?r)xZdyei(r?q)y~(q)~!(r) p2e?iqy~(q)Zdr1 p2e?ir(x?y)~!(r) 

=1 

F[]bezeichnedabeidieFourier-Transformation.Nungilt =p2~(p)~!(p): p23ZdqZdr2(p?r)2(r?q)~(q)~!(r) 

k!k2L2=Zdxj!j2 =ZdxF?1[F[!]]2 =ZdxZdp1 =ZdxZdpe?ipx~(p)~!(p)Zdqe?iqx~(q)~!(q) p2e?ipxp2~(p)~!(p)2 

=ZdpZdq2(p?q)~(p)~!(p)~(q)~!(q) =ZdpZdqZdxe?i(p?q)x~(p)~!(p)~(q)~!(q) 

DasvollendetdenBeweis. =2Zdpj~(p)j2j~!(p)j2 

Lemma2MitdemobigenLemmaundderHolderschenUngleichungfolgt k!k2L22k~k2L2mk~!k2L2n 2 

mit1m+1n=1,soferndieentsprechendenNormenexistieren.FallsdieseNormenexistieren,gelten wegen k~k2L2=kk2L2

mitm=1;n=1insbesonderediefolgendenUngleichungen: A.2.DASIMPLIZITEEULER-VERFAHREN 75 

Beweis:DieAussagenfolgendurchEinsetzen,weshalbnurdiemittlereIdentitatbewiesensei: k!k2L22k~k2L1k!k2L2: k!k2L22kk2L2k~!k2L1; 

k~k2L2=Zdp~(p)~(p) 

=ZdpZdx1 2ZdxZdyZdpei(x?y)p(x)(y) p2eipx(x)Zdy1 p2e?ipy(y) 

=Zdxj(x)j2 =1 2ZdxZdy2(x?y)(x)(y) 

=kk2L2: DasimpliziteEuler-Verfahren 2 

VerwendetmandasimpliziteEuler-Verfahren,soerhaltmanaus(A.1)und(A.2)furdieLosung A.2.1Verfahren u1zumerstenZeitschrittdieGleichungenu1=u0+kv1; DabeiistkdieZeitschrittweite.FurdiefolgendenZeitschrittegeltennaturlichanalogeFormeln. DiebeidenGleichungenlassensichin ?1?k2u1=u0+kv0; 

v1=v0+ku1: 

umformen.EsistalsonurnocheineechteGleichungzulosen,diezweiteGleichungisteineArt v1=1k?u1?u0 (A.5) (A.4) 

Postprocessing-Schritt. A.2.2Analyse DieGreenscheFunktionzumOperator(1?k2)istineinerDimensiondurch 

gegeben,sodafurdieNaherungu1gilt: g(y)=1 2ke?jyj 

u1=Z1 

k?u0(x?y)+kv0(x?y) k; 

?1dy1 2ke?jyj ku0(x?y)+Z1 ?1dy12e?jyj kv0(x?y): (A.6)

istundsomitdenkastenformigenIntegralkernimzweitenTermvon(A.3)einigermaenvernunftigannahert,zeigtderersteTermkeinerleiAhnlichkeitmitderexaktenLosung.Schaubilderder 

approximativenundderexaktenIntegralkernesindinAbbildungA.1zunden.BeideTermever- 

WahrendderzweiteTermtatsachlichimwesentlicheneineMittelunguberdenBereich?kyk 76 ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN 

letzendieEndlichkeitderAusbreitungsgeschwindigkeit,wasangesichtsdeselliptischenCharakters 

6 

5 

von(A.4)auchnichtweiteruberrascht. 

Exakt 


0.7 

0.6 

0.5 

Exakt 


4 

AbbildungA.1:ErsterundzweiterIntegralkernfurdasimpliziteEuler-Verfahrenbeik=1 

0.4 

3 

0.3 

10. 

0.2 

2 

0.1 

1 

0 

L1-Fehler 

-0.1 

0 

-0.2 

Esgiltwegen(A.3)und(A.6) 

-0.3 -0.2 -0.1 0 0.1 0.2 0.3 

-0.3 -0.2 -0.1 0 0.1 0.2 0.3 

mit ?u(k)?u1(x)=(au0)(x)+k(bv0)(x) 

a(y)=12(y?k)+12(y+k)?1 2ke?jyj (A.7) 

b(y)=1 2k(k?jyj)?1 2ke?jyj k: k; 

Ausbwurdeeinek-PotenzausGrunden,dieweiteruntenklarwerden,herausgezogen. Damitist ?u(k)?u1(x)=?a(y);u0(x?y)L2(y)+k?b(y);v0(x?y)L2(y) 

DaswollenwirgernedurchdieHolderscheUngleichungauswerten.FurdenerstenTermmit akommtdabeinurdieL1-NorminFrage,dadieL1-Normnichtexistiertundwirsonstnicht ?a(y);u0(x?y)L2(y)+k?b(y);v0(x?y)L2(y): 

furdenzweitenSummandenkonnenwirdieNormenmit1n+1m=1freiwahlen: wissen,wiewirzumBeispielfurdieL2-NormdasQuadrateinerDelta-Funktionauswertensollen; 

DierechteSeitehangtjetztnichtmehrvonxab.DieNormenvonaundbkonnenwirausrechnen underhaltenbeispielsweisefurm=n=2 ka(y)kL1(y)u0(x?y)L1(y)+kkb(y)kLm(y)v0(x?y)Ln(y): 

u(k)?u1L12u0L1+r1e?14pkv0L2: (A.8)

DawirnurdieOrdnungO(1)erhalten,istebensowiederVorfaktorkeintechnischesProblem A.2.DASIMPLIZITEEULER-VERFAHREN derAbschatzungvona,sonderneinescharfeAbschatzung,wiesichaneinemeinfachenBeispiel 77 

demonstrierenlat.SeiendafuralsAnfangswerte u0(x)=1furx=k; 

odereinegeeignete,gegendieseFunktionenkonvergierendeFunktionenfolgegegeben.NachA.3ist v0(x)=00sonst; 

dannu(0;k)=1,jedochistu1(0)=0nach(A.6).Damitistschonu(k)?u1L1=1=u0L1. DerVorfaktorlatsichmiteinemetwastechnischerenBeispieldemonstrieren,wennmanv0so setzt,dadiebeidenPunktwertevonu0nichtinjeweilsbeideRichtungenlaufen,sondernbeide ausschlielichzumUrsprunghin.Dortistdannu(0;k)=2,dieL1-Normvonu0hatsichaber nichtgeandert. Mit(A.7)ist L2-Fehleru(k)?u12L2=Zdx?a(y);u0(x?y)L2(y)+k2?b(y);v0(x?y)L2(y)2 

DiesmalistdieAufteilungmitderHolderschenUngleichungnichtmoglich,dadannausdemerstenTermdasIntegral2R1?1dx22u02L1entstehenwurde,alsoeinIntegralubereineKonstante, 

2Zdx?a(y);u0(x?y)2+2k2Zdx?b(y);v0(x?y)2: 

wasnaturlichdivergiert. Lemma1,soerhaltmanfurdenerstenTerm Manmuhierversuchen,dieLokalisierungvonabesserauszunutzen.Verwendetmanjedoch 

kennen: wobeiwir~aausderBerechnungvongundvonderFouriertransformiertenderDeltafunktionen ?au0(x)2L2=2Zdpj~aj2~u02; 

istderKosinuseineApproximationersterOrdnungfurdenBruchterm,dasheitderzweiteTerm DieserTermistohneAbschatzungzustandegekommenundlatsichwiefolgtdeuten:furkleinekp =2Zdpj~u0(p)j21 p2coskp? 1+k2p22: 1 

istbisetwakp=0:2klein.DerganzeTermistalsoklein,fallsj~u0(p)j2auerhalbvonjpj

gutist.Wiewirgleichsehenwerden,sindwirhauptsachlichanderL1-Normvon~ainteressiert. 78 Wirdenierendaher ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN 

DieseFunktionistleichtnumerischauswertbar. FurdenzweitenTermerhaltmanganzanalog: a21(s)=max ?sxscosx?1 1+x22: (A.9) 

Hattenwirnichteinkausbherausgezogen,sowurdederIntegrandauervonkpauchnochvonk abhangen.Integriertmanwiederfurkleinekp0nurdasersteReihenglied,soist?bv0(x)2L2 ?bv0(x)2L2=Zdpj~v0(p)j2sinkp kp? 1+k2p22: 1 

c2bp4+1 0 k4k~v0k2L2.Auerdemdenierenwirnoch 

Damithabenwirfurkleinekp0insgesamt b1(s)2=max ?sxssinx x?1 1+x22: (A.10) 

mitdemgewahltenp0unddenwiebeschriebenberechenbarenKonstantenc2a;b.Insbesondere erhaltmanwegenk~ukL2=kukL2mitn==1;m==1: u(k)?u12L2c2ap4+1m 0 k4k~u0k2L2n+c2bp4+1 0 k6k~v0k2L2; (A.11) 

DiebessereAbschatzungmitdennumerischauswertbarenFunktionena1undb1ergibt u(k)?u12L214p40k4ku0k2L2+25 

u(k)?u12L2a21(kp0)ku0k2L2+b21(kp0)k2kv0k2L2: 36p40k6kv0k2L2: 

UmeinevorgegebeneGenauigkeitzuerreichen,mussenwirksokleinwahlen,dadieVorfaktoren beigegebenemp0kleingenugwerden.a21undb21sindindenAbbildungenA.3furverschiedene 

Verfahrengegenubergestellt. 

Diskretisiertman(A.1)und(A.2)mitdemFractional--Verfahren,soerhaltmandiefolgenden A.3.1Verfahren Das-Verfahren 

beidenGleichungen: 

odernacheinerUmformung: u1=u0+k1v1+k(1?1)v0; 

(1?k212)u1=u0+kv0+k21(1?2)u0; v1=v0+k2u1+k(1?2)u0; 

DerAllgemeinheithalberhabenwirzweiverschiedeneKonstanten1,2gewahlt.Ebensowie v1=1 k1(u1?u0)?1?1 1v0: (A.12) 

beimimplizitenEuler-VerfahrenistauchhiernureineechteGleichungzulosen.

A.3.DAS-VERFAHREN A.3.2Analyse FurdieersteGleichungistdieGreenscheFunktiondurch 79 

gegeben,undwirerhaltenfurdiesemidiskretisierteLosungnacheinemZeitschritt g(x)= 2kp12e?jxj 1 

WirkonnendenAbleitungsoperatordurchpartielleIntegrationaufgwirkenlassenunderhalten mitderDenitionsgleichungvong: u1=?g?u0+kv0+k21(1?2)u0(x): (A.13) 

u1=Z1 ?1dy +Z1 ?1dy 2k2p12e?jyj 2p12e?jyj 

1 kp12v0(x?y): kp12?1?2 2(y)u0(x?y) 

bildungA.1)eineDeltafunktionabgezogen.ImFinite-Elemente-KontextkonnenwirdieseDel- 

tafunktionwohlalsHutfunktionderBreite2hundderHohe1hansehen.ImgunstigstenFallist h=k,dannergibtsichdieinAbbildungA.2gezeigteFunktion.FurandereWertevonhistdie Approximationschlechter,wasoftderFallseinwird,dawirwegendesimplizitenCharaktersdes VerfahrensdieZeitschrittweitegroeralshmachenkonnen. 

ImerstenIntegralkernwirdinderMittedesunerwunschtenexponentiellenPeaks(vgl.Ab- 

(A.14) 

Das,beidemdasVerhaltnisderabgezogenenFunktionzurExponentialfunktionmaximal 

10 

8 

wird,istwieerwartet=12,entsprechenddemCrank-Nicolson-Verfahren. 

Exakt 


1 

0.8 

Exakt 


AbbildungA.2:ErsterundzweiterIntegralkernfurdasCrank-Nicolson-Verfahrenbeik=110 

0.6 

6 

undlinksh=k. 

0.4 

4 

0.2 

2 

0 

L1-Fehler 

0 

-0.2 

-0.3 -0.2 -0.1 0 0.1 0.2 0.3 

-0.3 -0.2 -0.1 0 0.1 0.2 0.3 

DenFehlerkannmanmit(A.3)und(A.13)wiederals darstellen,mit ?u(k)?u1(x)=(au0)(x)+k(bv0)(x) (A.15) 

a(y)=12(y?k)+12(y+k)? b(y)=1 2k(k?jyj)? 2kp12e?jyj 1 2k2p12e?jyj kp12: 1 kp12+1?2 2(y);

80Wirerhaltenganzanalogzuoben 

ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN 

mit1m+1n=1.Wahltmanwiederm=n=2undrechnetdieIntegraleaus,soerhaltman ku(k)?u1kL1kak1ku0k1+kkbkLmkv0kLn; 

AuchhieristderVorfaktordeserstenTermswiederscharf,wofursichBeispieleanalogdem ku(k)?u1kL122ku0kL1+se?1 p12?12+ 4p12pkkv0kL2: 1 

obengezeigtenkonstruierenlassen.ImallgemeinenistderL1-FehlerbeidiesemVerfahrenalso 

L2-Fehler FormelfurdasimpliziteEuler-Verfahren. schlechteralsbeimimplizitenEuler-Verfahren.Fur1=2=1erhaltmannaturlichwiederdie 

Mangehtwiederebensowieobenvorunderhalt 

mit u(k)?u12L2au02L2+k2bv02L2 2k~ak2L2mk~u0k2L2n+2k2k~bk2L2k~v0k2L2 

k~ak2L2m=1 k~bk2L2=1 2(Zdpcospk?12 2(Zdpsin(kp) kp? 1+k212p22)1: 1+k212p2+1?2 11 

22m)1m; 

BetrachtetmandieerstenReihengliederderEntwicklungnachp,soergibtsich k~ak2m L2m=1 2Zdp(1?21)2k4p4 4+(1?21)(24212?1)k6p6 

k~bk2 L2=1 2Zdp(1?612)k4p4 +(8640412?2880312?240212?81+9)k8p8 36?(1?612)(1?120212)k6p6 242880+m; 

Wahltmanalso1=12und2=13undfuhrtwiederdieAbschneidefrequenzp0ein,soerhalt +(34142?133132?160212?1 252012+41 302400)p8k8+: 360 

mandiemaximaleOrdnung: k~ak k~bk2L2m1 

21 249 5762 1296002 8m+11mp8+1m 8+11p8+1 00k8: 

k8; 

Zusammenergabesichfurn==1;m==1: u(k)?u12L21 576p80k8ku0k2L2+49 129600p80k8kv0k2L2: (A.16)

AllerdingsistdasVerfahrenfurdieseWahlderinichtstabil. A.4.DASDG(1)-VERFAHREN Wahltmandagegenmit=12 81 

a21(s)=max b21(s)=max ?sxscosx?1 ?sxssin(x) x? 1+2x22; 1+2x+1? 1 

2; 

soergibtsichwiederu(k)?u12L2a21(kp0)ku0k2L2+b21(kp0)k2kv0k2L2: a21undb21sindwiederindenAbbildungenA.3zunden. 

DawegenderLinearitatderWellengleichungdasimpliziteEuler-Verfahrenidentischmitdem A.4.1Verfahren DasDG(1)-Verfahren 

Verfahrenbereitsobenhergeleitet.WirbetrachtendahernurnochdasDG(1)-Verfahren. unstetigenGalerkin-VerfahrennullterOrdnung,DG(0),ist,sinddieFehlergrenzenfurdieses MitU=(u;v)Tlassensich(A.1)und(A.2)als 

schreiben,wobeiBdieSystemmatrixsei.DasDG(1)-VerfahrenfurSystemeschreibtsich Ut=01 

U1?=Zk 0U=:BU 

U1??U0+=Zk 0BU(t)tkdt: 0BU(t)dt+U0?; 

SetztmanU(t)=tkU1?+k?t kU0+ein,soergibtsichdaraus 

U1??U0+=k3BU1?+k6BU0+; U1?=k2B(U1?+U0+)+U0?; 

oderwiederin"alter\Schreibweise:u1?=k2(v1?+v0+)+u0?; v1?=k2(u1?+u0+)+v0?; (A.17) 

u1??u0+=k3v1?+k6v0+; (A.19) (A.18) 

Aus(A.17)und(A.19)ergibtsichderPostprocessing-Schritt,umU1?zuerhalten: v1??v0+=k3u1?+k6u0+: (A.20) 

U1?=P+U0++P?U0?

mit 82 ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN 

DiebeidenMatrizenPpropagierensozusagendieLosungaufdemIntervall(0;k)voneinem Zeitschrittzumnachsten. P+=3?k2 6k?2; P?=?20 ?6k0: 

hinweghilft: Eingesetztin(A.18)und(A.20)ergibtsichdieGleichung,dieunsuberdenSprungint=0 6k?2k?2+k2 

A.4.2Analyse 6k?76k?3+k2 4 6!U0+=6k?k1 6k?23k0U0?: (A.21) 

MankannGleichung(A.21)diagonalisieren: mitdemMatrixoperator(@)=4(36?7k2)4k(18?k2) (144?76k2+k42)U0+=(@)U0?; 

DieseDarstellungistzwarfurdieNumerikungeeignet,dasiezuvielRegularitatvonderLosung fordert;sieerlaubtabereineeinfachereAnalyse,dadieGreenscheFunktiong(y)zumOperator 4k(18?k2)4(36?7k2): 

nichts,dawirgauchgarnichtbrauchen,sonderndieFourier-Transformierte~g,diedirektdurch aufderlinkenSeiteskalarist.g(y)istindiesemFallnichtmehrberechenbar;dasmachtaber 

gegebenist. Damitgilt: ~g(p)=1 p2144+76k2p2+k4p4 

1 (A.22) 

undmitdenP-Matrizen U1?(x)=?gP+(@)U0?(x)+P?U0?(x) U0+=?g(@)U0?(x); 

Dagskalarist,vertauschtesmitdenMatrizenundwirkonnendiepartielleIntegrationeinfach durchfuhren: =Zdy?F?1[~g](x?y)P+(@y)+(x?y)P?U0?(y): 

EigentlichwurdemanimArgumentzudurchdiepartielleIntegrationeinanderesVorzeichen erhalten,dasjedochdurchdasVorzeichenvonyimArgumentzugwiederverschwindet.Man =Zdy?P+(@y)F?1[~g](y)+(y)P?U0?(x?y): 

kannnunmitunterdasIntegralderFouriertransformationziehenunderhaltdamit U0+(x)=ZdyF?1P+(?ip)~g+1 =?TU0?(x) p2P?(y)U0?(x?y)

A.5.BEDEUTUNGDERBEDINGUNG"~U(P)=0FURjPjP0\ mitderTransfermatrixT=F?1P+(?ip)~g+1 

83 

DarauserhaltenwirwiederunsereFehleridentitat: ?u(k)?u1(x)=(au0)(x)+k(bv0)(x) p2P?: 

mitdenGroen a(y)=12((y?k)+(y+k))?T11; 

b(y)=1 

DerL1-Fehleristdiesmalnichtsoleichtberechenbar,dawira(y)undb(y)nichtexplizitkennen,sondernnurderenFourier-Transformierten.Moglicherweiseistestrotzdemmachbar,indem 

manEigenschaftenderinversenFourier-Transformationtrickreichnutzt,umdieL1-Normder Integralkernezuberechnen;dieserWegseihierabernichtweiterverfolgt. 

2k(k?jyj)?1kT12: 

p0durch DieNormenderFourier-TransformiertenderIntegralkernesindjetztmitderAbschneidefrequenz L2-Fehler 

k~ak2L2m=1 k~bk2=1 

2(Zp0 ?p0dpcospk?2(216+60k2p2+k4p4) 

?p0dpsin(kp) kp? 144+76k2p2+k4p4+22m)1m; 

gegeben.DieseNormenhierexplizitzuberechnenistzwarmoglich(undergibtProportionalitaten 144+76k2p2+k4p42)1 144?2k2p2 

vergieren;insbesonderehabendieerstenTermedasgleicheVorzeichen.Wirdenierendeshalb wieder zup4+1m 0 k4undp4+1 0k4),istabernichtsinnvoll,dadieReihenentwicklungensehrschlechtkon- 

a21(s)=max b21(s)=max ?sxssinx ?sxscosx?2(216+60x2+x4) x? 144+76x2+x4+22; 

underhalten 144+76x2+x42; 144?2x 

A.5 BedeutungderBedingung"~u(p)=0furjpjp0\ u(k)?u12L2a21(kp0)ku0k2L2+b21(kp0)k2kv0k2L2: 

InderHerleitungderL2-FehlerabschatzungenwurdevonderBedingung 

BedingungerscheintaufAnhiebetwaswillkurlich,istaberbeigenauererBetrachtungdurchaus Gebrauchgemacht,umdieIntegraleasymptotischberechnenzukonnen.DieForderungdieser ~u(p)=0 fur jpjp0

84 ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN 

vernunftig:nimmtmanan,dadieBedingunggilt,sogibteseinegroteFrequenzp0inder 

Fourierentwicklungvonu(x;t).Die(raumlich)amschnellstenvariierendenAnteilevonu(x;t) 

habenalsodieFrequenzp0unddamitdieWellenlange=2 

p0. 

ImRahmenderspaterenraumlichenDiskretisierunglegenwirdurchdieWahleinerminimalen 

vetretbarenGitterweitefest,biszuwelcherGroenordnungwirdieEigenschaftenderexakten 

Losungapproximierenwollen.EinevernunftigeAuosungistbeispielsweisefurVariationender 

Wellenlange2hmitderOrtsgitterweitehgegeben(einePeriodeeinesSinusmitwenigerals 

zweiGeradenstuckenanzunaherngehtvernunftigerweisenicht).Wennwiralsosagen,dawirmit 

Gitterweitenbishinunterzu(zumBeispiel)h=0:01rechnen,dannimplizierenwir,dawirkeine 

VariationenderLosungmehrauosenkonnen,derenWellenlangekleinerals0=0:02ist.Das 

entsprichtabereinemaximalenFrequenzvonp0=2=100.InderPraxiserhaltmaneine 

vernunftigenumerischeLosungsogarnurfur10h:::20h. 

DarausfolgtfurdieFestlegungvonp0,daesalsdasMinimumderbeidenfolgendenGroen 

zuwahlenist: 

diegrotetatsachlichinderLosungvorhandeneFrequenz,fallsdieLosungglattistundwir 

diekleinstenEigenschaftenvonu(x)mitmehralszweiOrtsgitterweitenauosenwollen; 

oder 

diegroteFrequenz,diewiraufeinemgegebenenGitternochauosenkonnen,dasheit 

2h. 

IndenFallenwodieLosungglattgenugist(Fall1)istp0eineKonstanteundwirkonnenVorfaktorenwieCp20kTwiebeimEuler-VerfahrendurchWahlvonkbeliebigkleinmachen.Wollen 

wirzumBeispieleinerelativeGenauigkeitvon10Prozent(bezuglichderL2-Norm)erreichen,so 

mu12p20kT0:1sein.Nimmtmanbeispielsweisean,dawirbiszurZeitT=10rechnenwollen 

unddiekleinstenDimensionenvonu(x)bei1 

100liegen,wobeih

A.6.VERGLEICHDERVERFAHREN 85 

1 

0.1 


Fractional Theta 

DG(1) 

1 

0.1 


Fractional Theta 

DG(1) 

0.01 

0.001 

0.01 

0.001 

AbbildungA.3:VergleichderFunktionena21(s)undb21(s)furdieverschiedenenuntersuchten 

0.0001 

0.0001 

Verfahren. 

1e-05 

1e-05 

1e-06 

1e-06 

1e-07 

1e-07 

einerkleinstenWellenlangevon0.02unddamith0:01)ergibtdasbereitsfurdasFractional- 

1e-08 

1e-08 

0.001 0.01 0.1 1 10 

0.001 0.01 0.1 1 10 

furkdieobereSchranke510?5,alsoeinzweihundertsteldergrotenvernunftigenOrtsgitterweite. 

s 

s 

maximaleFehlerdarfdahernichtalsKriteriumfurdieWahlderZeitschrittweiteangesehenwerden. FurdieanderenVerfahrenistdasmaximalekumetlicheweitereGroenordnungenkleiner.Der 

a ∞ 

2 

b ∞ 

2

86 ANHANGA.APRIORIFEHLERSCHRANKENFURZEITSCHRITTVERFAHREN

ZusammenfassungundAusblick 

MethodenmitdualenFehlerschatzernzudienen. ImRahmendieserArbeitwurdenVerfahrenzuradaptivenLosungderWellengleichungininhomogenenMedienmittelsFinitenElementenentwickelt.DabeiwurdezuersteineDiskretisierungin 

OrtundZeitvorgestellt;alsGalerkin-VerfahrenistsieinderLage,alsFundamentderadaptiven 

ist.FurdieseGroekommennahezualleFunktionaleinFrage,diesichaufdieLosunganwenden lassen.DazugehorenunteranderemLinien-undGebietsintegrale,mitundohneIntegrationuber dienebendernumerischenLosungauchandieQuantitatangepatist,andermaninteressiert dieZeit,aberauchandereAuswertungen;derAnsatzistinsbesonderenichtauflineareZielfunktionalebeschrankt,eswurdenauchWegeaufgezeigt,wienichtlineareFunktionaleverwendetwerden 

undmitwelchemGewichtsiediestun. konnen.ZurBerucksichtigungderZielgroeistesnotig,einzweites,"duales\Problemzulosen, dasdieInformationenthalt,welcheOrtezueinemgegebenenZeitpunktzumErgebnisbeitragen, 

AufdieserBasiswurdeeinallgemeinerAnsatzentwickelt,dereserlaubt,Gitterzuerzeugen, 

dieUberlegenheitdesdualenFehlerschatzersubergleichformigeVerfeinerung,aberauchgegenuber "traditionellen\FehlerindikatorenaufderBasisderEnergienormzeigenlie.Eskonntegezeigt DabeiwurdeneineReihevonFallenmitverschiedenenZielfunktionalenuntersucht,beidenensich werden,daderdualeSchatzerinderLageist,erheblichezientereGitterzuerzeugen,mitdenen DieserFormalismuswurdeindendarauolgendenKapitelnaufeinigeBeispieleangewandt. 

sichdiegewunschteGenauigkeitmitdeutlichgeringererAnzahlanFreiheitsgradenberechnenlat. ChromosphareundKoronauntersucht.Eszeigtesich,dadieVerfeinerungmitdemEnergiefehlerindikatorguteErgebnissezeigte,wahrendderdualeFehlerschatzerimwesentlichennichtzu 

befriedigendenResultatenfuhrte.AlsGrundedafurkommenunzureichendeLinearisierungender ZielfunktionaleumdieprimaleLosung,diestarkeInhomogenitatdesMediumsundDiskretisierungsfehlerinFrage.AmBeispieldesEnergieussesdurcheineLiniekonntegezeigtwerden,da 

dieLinearisierunginderTatnursehrschlechtkonvergiert.Esistallerdingsnichtklar,obdiesder alleinigeGrundfurdasVersagenist;hiersindnochweitereUntersuchungennotig,umdiegenauen 

InderHauptanwendungderArbeitwurdederEnergietransportamUbergangzwischensolarer 

Fragengehoren: Grundezubestimmen. neuerFragenauf,diezuuntersuchenauszeitlichenGrundennichtmehrmoglichwaren.Zudiesen IstdasNichtfunktionierendesdualenSchatzersendgultig,d.h.divergierendieErgebnisse DieErgebnissedieserArbeit,vorallemamBeispielausderSonnenphysik,werfeneineReihe 

beschrankteZahlvonVerfeinerungenmitdemdualenSchatzerdurchgefuhrtwerden.Man vonMehrgitteralgorithmennichtmoglichwar,konntenausRechenzeitgrundennureinesehr beobachtetauchbeiderVerfeinerungmitdemEnergiefehlerindikator,dastarkeVeranderungendesGitterszuzeitweiliggestorterKonvergenzfuhrenkann;danachUmschalten 

stattnden,wareesmoglich,danurdieerstenSchrittedanacheindivergentesVerhalten vomEnergiefehlerindikatoraufdendualenSchatzergroereUmstrukturierungendesGitters suggerieren,anschlieendjedocheinebeschleunigteKonvergenzstattndet.Hierkonntenbe- 

Losungsalgorithmenvoraussetzt. reitswenigeweitereVerfeinerungsschritteIndiziengeben,wasjedocherheblichverbesserte 

auchbeiweitererVerfeinerung?DaimzeitlichenRahmendieserArbeitdieImplementation 

87

88WelchenEekthatdieschlechteLinearisierungdernichtlinearenZielfunktionale?Ausden 

berechnetenVerlaufendesEnergieussesdurchdieAuswertungsliniewurdemanerwarten, ZusammenfassungundAusblick 

einemerstenSchrittzuuntersuchen,obbeidemgegebenenProblemdieVerfeinerungmit demdualenSchatzerzueinemlinearenZielfunktionalzumErfolgfuhrt. dieschlechteLinearisierungtatsachlichfurdasVersagenverantwortlichist.Hierwarein wird;manerwarteteher,daderverfeinerteBereichzugroist.Esistdahernichtklar,ob daderFehlerschatzernichtdazufuhrt,daVerfeinerungandenrichtigenStellenunterlassen 

WelcheRollespielendiestarkvariierendenKoezienten?SiesolltendieKonvergenzvon schlechtenLinearisierungalsauchzuungenauerBerechnungderdualenLosungbeitragen. senerschwert.InvielenAnwendungenausderPraxissinddieVariationenderKoezienten damitdennumerischenAufwandzuderenInvertierungstark,wasweitereKonvergenzanaly- 

primalerunddualerLosungwesentlichverschlechternundkonntendaherdazusowohlzur DaruberhinausverschlechternsiedieKonditionderSystemmatrizenerheblichunderhohen wahrendsiehierbeinaheeinenFaktorTausendausmachte),sodadiegleichenVerfahren legendieseVermutungnahe. dorterfolgreichseinkonnten;einigedergerechnetennichtanwendungsbezogenenBeispiele erheblichgeringer(inderGeophysikbeispielsweiseinderGroenordnungvonunterzehn, 

Danebensindnochdiefolgenden,allgemeinerenFragenunbeantwortet: IstderdualeFehlerschatzerinderLage,teilweiseReexionanGitterunstetigkeitenzuerkennenundgegebenenfallszuverhindern,soferndasfurdieAuswertungdesZielfunktionals 

ZuwelchenErgebnissenfuhrtdieVerwendungandererMoglichkeitenderAuswertungder Fehleridentitat?DazuexistierennebenderskizziertenVerwendungdesBramble-Hilbert- notwendigist? 

aufdemPatch.LetztlichistdieErsetzungdesverwendetenVerfahrensdurcheinanderes LemmasdieExtrapolationeinernumerischendualenLosungaufeinenhoherenAnsatzraum unabdingbar,dasichdersehrerheblichezusatzlicheAufwandzurBerechnungderdualen LosunginderPraxiswederrechtfertigennochbereitstellenlat.ErsteExperimenteindiese 

WeshalbwurdeeinVersagendesKonzeptsderdualenFehlerschatzerbisherniebeobachtet? Richtunglassenvermuten,dasichdieQualitatdererzeugtenGitternichtwesentlichandert; diesausreichendzurVerwendung"billigerer\Fehlerschatzer. daquantitativeFehlerschatzungindenmeistenFallenohnehinnichtmoglicherscheint,ist WasunterscheidetdieWellengleichungvondenbisherbetrachtetenSystemen?Sowohlbei lerschatzererfolgreichangewandt.DieseGleichungenwurdenallerdingsentwederzeitun- 

alsauchbeizeitabhangigenProblemenwiederWarmeleitungsgleichungwurdendualeFeh- 

nichtlinearenGleichungenwiederElasto-PlastizitatoderdenNavier-Stokes-Gleichungen, 

fungseigenschaftenundFehlerakkumulationbeizeitabhangigenProblemeninKombination schaften(Warmeleitung),sodaesdenkbarist,daerstdievolligeAbwesenheitvonDamp- 

abhangiggelost(Elasto-Plastizitat,Navier-Stokes),oderhattenstarkdiusiveEigen- 

Abschlieendlatsichsagen,dadieVorteileadaptiverVerfahrengegenuberglobalerVerfeinerungdeutlichgezeigtwerdenkonnte,ebensowiedieUberlegenheitdesdualenSchatzersgegenuber 

traditionellenFehlerindikatorenbeieinfachenProblemen.AllerdingsscheitertediesesVerfahrenin einemkomplexenAnwendungsfallausderPraxisweitgehend;dieGrundedesScheiternssindzueinemerheblichenTeilunverstandenundbietenStoundAnlafurweiterfuhrendeUntersuchungen 

gelangen.DieseVermutungistbisherallerdingsinkeinerWeiseuntermauert. denBereichderKonvergenzderBerechnungvonFehlerschatzernundGitterverfeinerungzu mitdenhohenrechentechnischenAnforderungendazufuhrten,daesnichtmoglichwar,in 

aufdiesemGebiet.

Notationen 

w=(u;v) wh=(uh;vh) wnh=(unh;vnh) ExakteLosung 

e=w?wh wh=(uh;vh) w=(u;v) ExaktedualeLosung NumerischeApproximationderdualenLosung NumerischeApproximationderLosungzumZeitpunkttn 

t=('; Wh th=('h; ) h) TestfunktiondeskontinuierlichenProblems TestfunktiondesdiskretenProblems FehlerzwischenexakterundnumerischerLosung 

kn Th hK tn?tn?1ZeitschrittweiteimntenZeitintervallIn DiskreterTestraum DurchmesserderZelleK DiskreterAnsatzraum 

Tn (x) a(x) (f;g) Dichte Steigkeitskoezient TriangulierungdesGebietsaufdemZeitintervallIn 

kuk Rdxf(x)g(x) (u;u)1=2 

a(u;v) A ?ra(x)r Laplace-OperatorPdi=1@2 

B (a(x)ru;rv)[0;T] 0?(x) @x2i 

b(w;t) 0 Aa(x)r0w;10 

0? 

gD gN Zielfunktional Dirichlet-Randwerte Neumann-Randwerte0rt[0;T]?(gN;t2)?N[0;T] 

ExaktesFehlerfunktional 

K;n EK;n J()=J()?~J()LinearisierungsfehlerdesFehlerfunktionals LinearisiertesFehlerfunktional FehlerschatzerfurKInzumFehlerJ(e) ExakterBeitragvonKInzumFehlerJ(e) 

89

90 Notationen

Literaturverzeichnis 

[1]NajibA.AbboudandPeterM.Pinksky.Finiteelementdispersionanalysisforthethreedimensionalsecond-orderscalarwaveequation.Int.J.Numer.Meth.Eng.,35:1183{1218, 

[2]ShinAoiandHiroyukiFujiwara.3-dnite-dierencemethodusingdiscontinuousgrids.submittedtoBSSA,1998. 

1992. 

[3]WolfgangBangerth. [4]RolandBecker.AnadaptiveniteelementmethodfortheincompressibleNavier-Stokesequationsontime-dependentdomains.Doktorarbeit,UniversitatHeidelberg,1995. 

deal.IItechnicalreference. UniversitatHeidelberg, http://gaia.iwr.uni-heidelberg.de/~wolf,1998. 

[5]RolandBecker,GuidoKanschat,andFranz-TheoSuttmeier.DEAL{adierentialequations [6]RolandBeckerandRolfRannacher.Afeed-backapproachtoerrorcontrolinniteelement analysislibrary.Technicalreport,Preprint,IWR,UniversitatHeidelberg,1995. 

[7]S.C.BrennerandR.L.Scott.TheMathematicalTheoryofFiniteElements.Springer, methods:Basicanalysisandexamples.East-WestJ.Numer.Math.,4(4):237{264,1996. 

[8]M.O.Bristeau,R.Glowinski,andJ.Periaux.NumericalmethodsfortheNavier-Stokes Berlin-Heidelberg-NewYork,1994. 

[9]AnatoliyG.Butkovski.Green'sFunctionsandTransferFunctionsHandbook.SeriesinMathematicsanditsApplications.EllisHorwoodLtd.,NewYork,Brisbane,Chichester,Toronto, 

equations:applicationstothesimulationofcompressibleandincompressibleviscousows. ReportUH/MD-4,Univ.ofHouston,inComputerPhysicsReport,1987. 

[10]MatsCarlssonandRobertF.Stein.Radiationshockdynamicsinthesolarchromosphere{ 1982. 

[11]C.Cerjan,D.Koslo,R.Koslo,andM.Reshef.Anonreectingboundaryconditionfor resultsofnumericalsimulations.InMatsCarlsson,editor,Proceedingsofamini-workshop 1994. heldatInstituteofTheoreticalAstrophysics,UniversityofOslo,Norway,June6-8,1994, 

[12]R.ClaytonandB.Engquist.Absorbingboundaryconditionsforacousticandelasticwave equations.Bull.Seism.Soc.Am.,67:1529{1540,1977. discreteacousticandelasticwaveequations.Geophysics,50:705{708,1985. 

[13]RichardCourant,K.O.Friedrichs,andHansLewy.UberdiepartiellenDierentialgleichungen [14]BjornEngquistandAndrewMajda.Absorbingboundaryconditionsforthenumericalsimulationofwaves.Math.Comp.,31(139):629{651,July1977. 

derMathematischenPhysik.MathematischeAnnalen,100:32{74,1928. 

91

92 [15]J.M.Fontenla,E.H.Avrett,andR.Loeser.Energybalanceinthesolartransitionregion.III. Heliumemissioninhydrostatic,constant-abundancemodelswithdiusion.Ap.J.,406:319{ LITERATURVERZEICHNIS 

[16]DonaldA.FrenchandToddE.Peterson.Acontinuousspace-timeniteelementmethodfor 345,March1993. 

[17]M.J.Grote.Nonreectingboundaryconditionsforelectromagneticscattering.Research Report98-09,SeminarfurAngewandteMathematik,EidgenossischeTechnischeHochschule, Zurich,September1998. thewaveequation.Math.Comp.,65(214):491{506,April1996. 

[19]RalfHartmann.A-posterioriFehlerschatzungundadaptiveSchrittweiten-undOrtsgittersteuerungbeiGalerkin-VerfahrenfurdieWarmeleitungsgleichung.Diplomarbeit,Universitat 

ResearchReport98-08,SeminarfurAngewandteMathematik,EidgenossischeTechnische [18]M.J.GroteandJ.B.Keller.Exactnonreectingboundaryconditionforelasticwaves. Hochschule,Zurich,September1998. 

[20]R.L.Higdon.Absorbingboundaryconditionsforacousticandelasticwaveequationsin Heidelberg,1998. 

[21]PatrickJoly.Developmentsinnumericalmethodsfortransientscatteringproblems.InGuy stratiedmedia.J.Comp.Phys.,101:386{418,1992. 

[22]GuidoKanschat.ParallelandadaptiveGalerkinmethodsforradiativetransferproblems. oftheconferenceheldinAix-les-Bains,France,September23{27,1996,LectureNotesin ChaventandPierreC.Sabatier,editors,InverseProblemsofWavePropagation.Proceedings 

Doktorarbeit,UniversitatHeidelberg,1996. Physics486.Springer,1997. 

[23]D.W.Kelly,J.R.Gago,O.C.Zienkiewicz,andI.Babuska.Aposteriorierroranalysis [24]P.KloucekandF.S.Rys.Onthestabilityoffractionalstep-schemeforthenonstationary andadaptiveprocessesintheniteelementmethod.Internat.J.Numer.MethodsEngrg., 19:1593{1619,1983. 

[25]PeterKorevaar.Time-dependentmodelsofstellarcoronae.Doktorarbeit,Rijksuniversiteit Utrecht,1989. Navier-Stokesequations.SIAMJ.Numer.Anal.,31(5):1312{1335,1994. 

[26]Y.Q.Lou,R.Rosner,andP.Ulmschneider.Acomputationalcodefortwo-dimensional [27]S.Muller,A.Prohl,R.Rannacher,andS.Turek.Implicittime-discretizationofthenonstationaryincompressibleNavier-Stokesequations.InW.HackbuschandG.Wittum,editors,Fast 

April1987. unsteadymagnetohydrodynamicsbythemethodsofcharacteristics.Ap.J.,315:349{370, 

[28]R.Rannacher.Numericalanalysisofnonstationaryuidow.Asurvey.InV.C.Boand SolversforFlowProblems,ProceedingsofthetenthGAMM-Seminar,KielJanuary14{16, 1994.F.Vieweg&SohnVerlagsgesellschaftmbH,Braunschweig/Wiesbaden,1994. 

[29]EndreSuliandCatherineWilkins.Adaptiveniteelementmethodsforthedampedwave H.Neunzert,editors,ApplicationsofMathematicsinIndustryandTechnology,pages34{53. B.G.Teubner,Stuttgart,1989. 

[31]J.Theurer,P.Ulmschneider,andW.Kalkofen.Acousticwavepropagationinthesolar [30]Franz-TheoSuttmeier.PrivateMitteilung. equation.Reportno.96/23,OxfordUniversityComputingLaboratory,1996. 

atmosphere.V.Observationversussimulation.Astron.Astrophys.,324:717{724,1997.

LITERATURVERZEICHNIS [32]JoachimTheurer.GenerationandPropagationofAcousticWaveSpectrainLate-TypeStellar Atmosphere.Doktorarbeit,UniversitatHeidelberg,1998. 93 

[33]PeterUlmschneider.Acousticwavesinthesolaratmosphere.VIII.Extrapolationintime. [34]J.E.Vernazza,E.H.Avrett,andR.Loeser.Structureofthesolarchromosphere.III.Models Astron.Astrophys.,168:308{310,1986. 

[35]J.Virieux.P-SVwavepropagationinheterogeneousmedia:velocity-stressnite-dierence oftheEUVbrightnessofthequietsun.Ap.J.Supp.,45:635{725,April1981. method.Geophysics,51:889{901,1986.

Adaptive Finite-Elemente-Methoden zur L osung der ...

Erfolgreiche ePaper selbst erstellen

Template löschen?

Als Template speichern?