Approximationstheorie

152 7 WAVELETS
orthonormal. Dafür gibt es stetige Funktionen, die orthonormale Skalierungsfunktionen sind,
nämlich beispielsweise die Orthonormalisierung der B–Splines nach Satz 7.8. Und es gibt eine
orthonormale Skalierungsfunktion mit kompaktem Träger, nämlich χ, aber die ist nun wieder
nicht stetig! Es scheint wie verhext! Gibt es also überhaupt Skalierungsfunktionen, die
1. stetig sind,
2. orthonormal sind,
3. kompakten Träger haben?
Die Antwort ist nicht nur “ja”, es gibt sogar Skalierungsfunktionen, die beliebig oft differenzierbar
und orthogonal sind und obendrein kompakten Träger haben! Ein Konstruktionsverfahren
für solche Wavelets wurde von Ingrid Daubechies erstmals in [15] angegeben. Beispiele für
solche Funktionen können in Abb. 7.4 und Abb. 7.5 bewundert werden.
1.4
1.2
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-1 0 1 2 3 4 5 6
line 1
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3
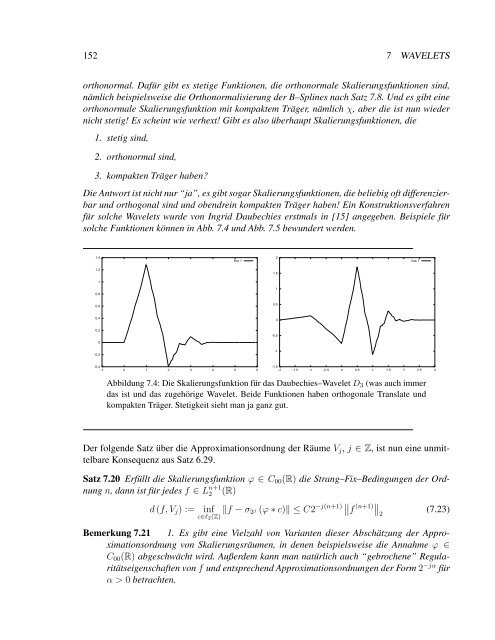
Abbildung 7.4: Die Skalierungsfunktion für das Daubechies–Wavelet D3 (was auch immer
das ist und das zugehörige Wavelet. Beide Funktionen haben orthogonale Translate und
kompakten Träger. Stetigkeit sieht man ja ganz gut.
Der folgende Satz über die Approximationsordnung der Räume Vj, j ∈ Z, ist nun eine unmittelbare
Konsequenz aus Satz 6.29.
Satz 7.20 Erfüllt die Skalierungsfunktion ϕ ∈ C00(R) die Strang–Fix–Bedingungen der Ord-
(R)
nung n, dann ist für jedes f ∈ L n+1
2
d (f, Vj) := inf
c∈ℓ2(Z) f − σ 2 j (ϕ ∗ c) ≤ C2−j(n+1) f (n+1) 2
line 1
(7.23)
Bemerkung 7.21 1. Es gibt eine Vielzahl von Varianten dieser Abschätzung der Approximationsordnung
von Skalierungsräumen, in denen beispielsweise die Annahme ϕ ∈
C00(R) abgeschwächt wird. Außerdem kann man natürlich auch “gebrochene” Regularitätseigenschaften
von f und entsprechend Approximationsordnungen der Form 2 −jα für
α > 0 betrachten.