pr ¨ufung tm iii und tm iii,iv - Lehrstuhl für Technische Mechanik ...

ERGEBNISSE
PRÜFUNG TM III UND TM III,IV
Lehrstuhl für Technische Mechanik, Universität Kaiserslautern
1. Aufgabe: (MV, BI)
m4
Prof. Dr.-Ing. P. Steinmann
l
WS 03/04, 03.03.2004
A B
g
m1
ϕ
R
S1
l
2
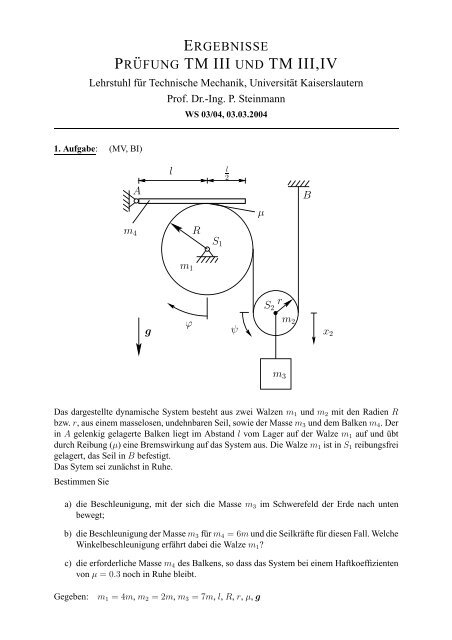
Das dargestellte dynamische System besteht aus zwei Walzen m1 und m2 mit den Radien R
bzw. r, aus einem masselosen, undehnbaren Seil, sowie der Masse m3 und dem Balken m4. Der
in A gelenkig gelagerte Balken liegt im Abstand l vom Lager auf der Walze m1 auf und übt
durch Reibung (µ) eine Bremswirkung auf das System aus. Die Walze m1 ist in S1 reibungsfrei
gelagert, das Seil in B befestigt.
Das Sytem sei zunächst in Ruhe.
Bestimmen Sie
ψ
a) die Beschleunigung, mit der sich die Masse m3 im Schwerefeld der Erde nach unten
bewegt;
b) die Beschleunigung der Masse m3 für m4 = 6m und die Seilkräfte für diesen Fall. Welche
Winkelbeschleunigung erfährt dabei die Walze m1?
c) die erforderliche Masse m4 des Balkens, so dass das System bei einem Haftkoeffizienten
von µ = 0.3 noch in Ruhe bleibt.
Gegeben: m1 = 4m, m2 = 2m, m3 = 7m, l, R, r, µ, g
µ
S2
r
m3
m2
x2

9m −
a) ¨x2 =
3
2 µm4
g
18m
1 − µ
b) ¨x2 = g,
2
¨ϕ = 2
R ¨x2
1 − µ
=
R g
SI = 2 + 5
2 µ
mg
5
SII = + 2µ mg
2
c) m4 = 20m

2. Aufgabe: (MV, BI)
l
l
cF
B
A
C
2
3
cM2
1
4
l
l
Das dargestellte, ebene System bestehe aus vier masselosen Körpern, einer Normalkraftfeder
cF sowie einer Drehfeder cM2. Die starren Körper 1, 2 und 3 sind durch Momentengelenke in
A und B miteinander verbunden. Der Körper 4 besitze die Biegesteifigkeit EI und sei in C fest
an den Körper 3 angeschlossen.
Bestimmen Sie
a) ein Ersatzsystem, das für die dargestellte Belastung F geeignet ist,
b) die kritischen Lasten sowie die zugehörigen Knickformen des infinitesimal ausgelenkten,
zutreffenden Ersatzsystems unter den Annahmen cF = 11 EI
l3 und cM2 = 3 EI
.
l
Gegeben: l, EI, cF , cM2
a)
ϕ2
ϕ1
cF
F
cM2
cM1 = 3 EI
l
cM1
b)
0,17
l
0,83
F1 = 7.36 EI
l 2
F
2,2
1,2
F1 = 23.64 EI
l 2

3. Aufgabe: (MV, BI)
h
00000000000000000000
11111111111111111111
00000000000000000000
11111111111111111111
00000000000000000000
11111111111111111111
B
C
m1
ℓ
45 ◦
A
Eine Punktmasse m1 wird durch einen masselosen starren Stab der Länge ℓ, der im Punkt B
befestigt ist, gehalten. Der Stab schließt im Punkt B mit der vertikalen einen Winkel von 45 ◦
ein. Eine ruhende, homogene Kreisscheibe (Masse m2 , Radius R, Schwerpunkt S) ist im Punkt
C gelenkig gelagert. Unter dem Einfluss der Schwerkraft bewegt sich die Punktmasse m1 auf
die Kreisscheibe zu und trifft sie im Punkt A (die Punkte A und S liegen auf einer Geraden).
Der Stoß erfolgt elastisch.
Bestimmen Sie
a) die Winkelgeschwindigkeit ω1a der Punktmasse kurz vor dem Stoß;
b) die Winkelgeschwindigkeit ω2b der Kreisscheibe kurz nach dem Stoß;
c) den Geschwindigkeitsvektor v2b des Kreisscheibe im Punkt A kurz nach dem Stoß;
d) die Stoßkräfte im Auflager C.
Gegeben: m1, m2, ℓ, R, h, g
a) ω1a =
b) ω2b = 1
R
c) v A 2bn
v A 2bt
g
l (2 − √ 2)
= R ω2b
= −R ω2b
4m1
2m1 + 3m2
d) Ĉn = − 1
2 m2 R ω2b
Ĉy = 0
ω1a
S
R
m2
g

4. Aufgabe: (MV)
A
a
l
c
Ein starrer, masseloser Arm der Länge l ist in A drehbar aufgehängt und durch eine Feder mit
der Federkonstanten c abgestützt. Am freien Ende trägt er die Punktmasse m mit einem Zeiger,
der je nach Vertikalbewegung des Gehäuses die Ausschläge des Armes auf einer Skala anzeigt.
Das Gehäuse des Schwingungsmessgerätes wird nach dem Gesetz xE(t) = ˆxE sin Ωt bewegt.
Bestimmen Sie für kleine Auslenkungen
1. a) die Bewegungsgleichung des Massenpunktes im Bezug auf das Gehäuse.
b) die Eigenfrequenz des Schwingers in Abhängigkeit gegebener Größen.
2. a) die Lösung der Bewegungsgleichung für den eingeschwungenen Zustand.
b) die Phasenverschiebung der Lösung gegenüber der Erregerschwingung.
m
3. das Verhältnis a(Ω)
(in Abhängigkeit von Ω), so dass die gemessene Amplitude doppelt
l
so groß ist wie die Erregeramplitude ˆxE.
Gegeben: a, l, m, c, xE = ˆxE sin(Ωt)
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
Hinweis: Gravitation kann vernachlässigt werden

1. a) x = xE + xr
¨xr + c
a
2 xr = ˆxEΩ
m l
2 sin(Ωt)
b) ω2 = c
a
2 m l
2. a) xr(t) =
3.
b) ϕ = π
a
l =
V = 2 : a
l =
c
m
−Ω2 2 a
l
m
c
m
2c Ω
− Ω 2
V − 1
V
Ω
ˆxE sin(Ωt − π)

5. Aufgabe: (MV)
A
c1
m1
x
Auf einer horizontalen Unterlage bewegt sich reibungsfrei ein starrer Körper (Masse m1), der
über eine Feder (Steifigkeit c2, Länge l) mit einem gelenkig gelagerten starren Balken (Masse
m2, Länge R) verbunden ist. Weiterhin ist der starre Körper (m1) mit der im Punkt A gelagerten
Feder (Steifigkeit c1) verbunden. Die Bewegungen des starren Körpers und des starren Balken
sollen durch die generalisierten Koordinaten x und ϕ beschrieben werden. Die Federn (c1, c2)
seien für x = 0 und ϕ = 0 entspannt.
Bestimmen Sie unter Verwendung der Koordinaten x und ϕ
a) die potentielle Energie Π = Π(x, ϕ) des Gesamtsystems
b) die kinetische Energie T = T(x, ϕ, ˙x, ˙ϕ) des Gesamtsystems
c) die Bewegungsgleichungen für große Auslenkungen mit den LAGRANGEschen Gleichungen
2. Art
Gegeben: c1, c2, l, m1, m2, R, g
a) Π(x, ϕ) = 1/2c1x 2
+ 1/2c2((R sin ϕ − x) 2 + (R − R cosϕ) 2 )
+ m2g(−1/2Rcos ϕ + 1/2R)
b) T(x, ϕ, ˙x, ˙ϕ) = 1/2m1¨x 2 + 1/2Θ¨ϕ 2 mit Θ = m2l 2 /3
c) m1¨x + c1x − c2R sin ϕ + c2x = 0
Θ¨ϕ + 1/2R(−2c2 cos ϕx + 2c2R sin ϕ + m2g sin ϕ) = 0
l
c2
m2
ϕ
R
g