f x2 ( ) ( ) f x2 ( ) ( ) f x2 ( ) ( ) f x2 ( ) ( ) f x2 - MatheNexus

Eine Funktion heißt monoton abnehmend, wenn für alle x ∈D gilt: x1 < x2 ⇔ f x1 Gilt sogar x1 < x2 ⇔ f x1 Untersuche dazu:
( ) − f( x2)
f x1
f x1
x1 − x2
( ) − f( x2)
x1 − x2
Eigenschaften ganzrationaler Funktionen (2)
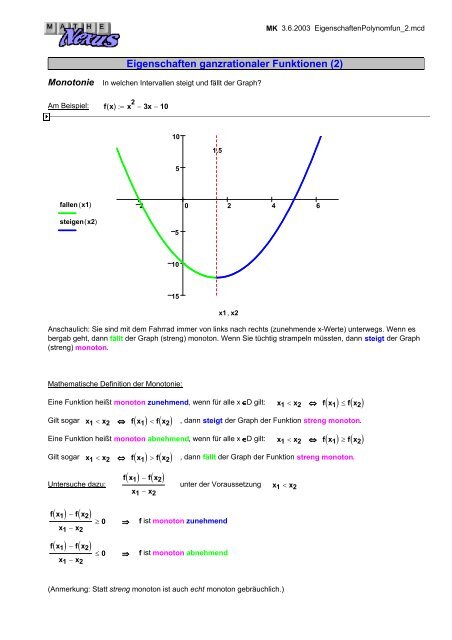
Monotonie In welchen Intervallen steigt und fällt der Graph?
Am Beispiel: f( x)
x 2
:= − 3x − 10
fallen ( x1)
steigen( x2)
f x1
2 0 2 4 6
( ) f( x2) ( ) − f( x2)
x1 − x2
( ) ≥ f( x2) > , dann fällt der Graph der Funktion streng monoton.
≥ 0 ⇒ f ist monoton zunehmend
≤ 0 ⇒ f ist monoton abnehmend
unter der Voraussetzung x1 < x2 (Anmerkung: Statt streng monoton ist auch echt monoton gebräuchlich.)
10
5
5
10
15
1.5
x1 , x2
MK 3.6.2003 EigenschaftenPolynomfun_2.mcd
Anschaulich: Sie sind mit dem Fahrrad immer von links nach rechts (zunehmende x-Werte) unterwegs. Wenn es
bergab geht, dann fällt der Graph (streng) monoton. Wenn Sie tüchtig strampeln müssten, dann steigt der Graph
(streng) monoton.
Mathematische Definition der Monotonie:
Eine Funktion heißt monoton zunehmend, wenn für alle x ∈D gilt: x1 < x2 ⇔ f x1 Gilt sogar x1 < x2 ⇔ f x1 ( ) f( x2) ( ) ≤ f( x2) < , dann steigt der Graph der Funktion streng monoton.

Am Beispiel:
Annahme:
Annahme:
Rechnung
analog:
f( x)
x 2
:= − 3x − 10
( ) − f( x2) f x 1
⎛
⎝
x 1 2
( x1 + x2) ⋅ ( x1 − x2) − 3 ⋅ x1 − x2 x1 + x2 − 3 ≥ 0
x1 + x1 + h − 3 ≥ 0
3 h
x1 ≥ −
2 2
( ) − f( x2) f x 1
x1 − x2 2
− 3 ⋅ x1 − x2 + 3 ⋅ x2 x1 − x2 3 h
x2 ≤ +
2 2
≥ 0
( )
x1 − x2 x1 − x2 ≤ 0
Also: Der Graph von f fällt monoton bis 1.5 und steigt dann monoton
Ein anschauliches Beispiel: Finde die Intervalle, in denen der Graph der Funktion steigt und fällt.
EigenschaftenPolfunMonotonie.gxt
Graph monoton steigend
⎞
⎠
≥ 0
( )
Es war
≥ 0
x2 = x1 + h
3
Man sieht, dass für sehr kleine h nur Werte x1 ≥ in Frage kommen.
2
Graph monoton fallend
mit
h > 0
, da Voraussetzung
3
Man sieht, dass für sehr kleine h nur Werte x2 ≤ in Frage kommen.
2
x1 < x2

Beschränktheit
Def.:
Bsp.:
Bsp.:
f1( x)
f2( x)
f3( x)
Eine Funktion heißt beschränkt, wenn es eine Zahl K ∈R oder eine Zahl L ∈R gibt, so dass gilt:
f( x)
≤ K
f( x)
≥ L
Es gilt auch
für alle x
für alle x
f2( x)
2 x 2
− x 4
:= −
f3( x)
:= sin( x)
Dann ist K eine obere Schranke.
Dann ist L eine untere Schranke.
Die kleinstmögliche obere Schranke heißt Supremum und die größtmögliche untere Schranke heißt Infimum.
, da x 2
f1( x)
x Es gilt f1( x)
≥ 1 ≥ 0
2
Bis auf Ausnahmen lässt sich zu diesem Zeitpunkt eine Schranke nur anschaulich (ohne Beweis) angeben.
Bsp.: := + 1
f1( x)
≥ −5
Damit wäre -5 eine untere Schranke. Das Infimum hier wäre 1.
Es gilt
Es gilt
f2( x)
≤ 2
−1 ≤ f( x)
≤ 1
5
4
3
2
1
6 4 2 0 2 4 6
1
2
3
4
5
x
Hier wäre 2 das Supremum
Diese Funktion hat eine obere und untere Schranke.

Aufgabe: Stelle mit Hilfe von GEONExT Schätzungen für Supremum/Infimum der Graphen fest.
blau
grün
rot
EigenschaftenPolfunSchranke1.gxt
EigenschaftenPolfunSchranke2.gxt
EigenschaftenPolfunSchranke3.gxt

Lösungen: (Die Berechnung mit Mathcad ist in der 11. Klasse noch nicht nachzuvollziehen)
g1( x)
0.1 x 4
⋅ 0.3 x 3
:= − ⋅ − 0.5x + 1
d
z1 := g1( x)
dx
= 0
Infimum_1 := g1( z12) g2( x)
−0.01 ⋅ ( x + 3)
⋅ ( x + 2)
( x − 1)
2
:=
⋅ ⋅ ( x − 4)
⋅ ( x − 5)
d
z2 := g2( x)
= 0 auflösen, x
dx
Supremum_2 := g2( z23) g3( x)
:= 2 ⋅ sin( 0.25x)
− 3 ⋅ cos( x)
d
z3 := g3( x)
= 0 auflösen, x
dx
Infimum_3 := g3( z31) Supremum_3 := g3( z34) auflösen, x
→
gleit , 4
→
Supremum_2 = 1.56
→
⎛
⎜
⎜
⎜
⎝
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
Infimum_3 = −5
− .1035 − .7057 ⋅ i
− .1035 + .7057 ⋅ i
2.457
Infimum_1 = −1.034
1.
−.92419299192762847387
2.9241929919276284739
−2.6005760645323503802
4.6005760645323503802
6.2831853071795864769
−6.2831853071795864769
−12.399070357617652414
−9.5464591313372454953
9.3101022848760373807
3.2562683294831355732
−3.0199114830219274586
−.16730025674152053962
Supremum_3 = 4.434
⎞ ⎟⎟
⎟
⎠
⎞ ⎟⎟
⎟
⎟
⎟
⎟
⎠
Ein Infimum existiert nicht, da
⎞ ⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠
⎯⎯⎯→
g2( z2)
=
⎯⎯⎯→
g3( z3)
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
−1
−5
−3.042
1.607
4.434
4.434
1.607
−3.042
0
−2.412
−2.412
1.56
1.56
⎞ ⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠
⎞ ⎟⎟
⎟
⎟
⎟
⎟
⎠
g2( x)
x --> ∞
--------------> ∞

x1 < x2 x1 + x2 < x2 + x2 0 ≤ x1 + x2 − 3 < x2 + x2 − 3
0 < 2x2 − 3
3
<
x2 2