Abschlussprüfung an Fachoberschulen in Bayern ... - MatheNexus

fa( a , 0)
→ −2
1P f( a , 0)
→ 0
=> Alle Tangenten besitzen einen gemeinsamen Punkt (Ursprung) und die gleiche Steigung (-2) 1P
5 1.4 Berechnen Sie a so, dass der Graph G fa bei x 0 = 2 einen relativen Extrempunkt hat. Bestimmen
fa( a , 2)
= 0
faa( x)
Sie Art und Koordinaten dieses Extrempunktes.
8
→ − 2 = 0 auflösen, a → 4 2P
a
fa 4 x
x ,
d
3
( )
d
4 x2
:= → ⋅ 1P faa( 2)
= 3 > 0 => Min 1P
f( 4 , 2)
= −3
=> Min( 2; -3) 1P
Für alle folgenden Teilaufgaben ist ist a = 4 und f4( x)
:=
1
16 x4
− 2x
4 1.5.Ermitteln Sie das Krümmungsverhalten des Graphen G f4 und untersuchen Sie, ob Wendepunkte
faa( x)
vorliegen.
3
4 x2 → ⋅ faa( x)
≥ 0 in ganz R => Gf4 ist in ganz R konkav (Linksg.) 3P
Wenn es keinen VZW der 2. Ableitung gibt, dann gibt es auch keine Wendepunkte 1P
5 1.6 Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und geeigneter Funktionswerte den Graphen
xs := −2 , −1.99
.. 4
MK 16.6.2005 A5_12NT_A2_MK_Loes.mcd
Abschlussprüfung an Fachoberschulen in Bayern
Mathematik 2005 Analysis A2 Ausbildungsrichtung Nichttechnik
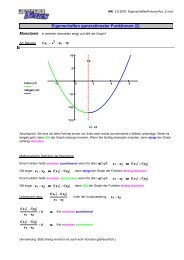
1.0 Gegeben sind die reelle Funktionen fa : x--> 1
4a x4 − 2x mit a € R und a > 0 und Dfa = R.
Der Graph einer solchen Funktion wird mit G fa bezeichnet.
2 1.1 Geben Sie das Verhalten der Funktionswerte für x -> ∞ f und x -> − ∞ an.
lim
x → ∞
f( a , x)
= ∞ 1P
lim
x → − ∞
f( a , x)
= ∞ 1P
4 1.2 Berechnen Sie die Nullstellen der Funktion fa und geben Sie auch die zugehörigen Vielfachheiten an.
1
4a x4
⎛
x
− 2x x
3
= ⋅ ⎜ − 2⎟
= 0 1P => x1 = 0 (einfach) 1.5P
4a
⎝
x 3
4a
⎞
⎠
− 2 = 0 => x 3
= 8a => x2 2 3 = a (einfach) 1.5P
3 1.3 Zeigen Sie rechnerisch, dass alle Graphen G fa im Ursprung diesselbe Tangente besitzen.
fa( a , x)
f a x
x ,
d
1
( )
d
a x3
:= → ⋅ − 2 1P
Gf4 für −2 ≤ x ≤ 4 in ein Koordinatensystem. Maßstab auf beiden Achsen 1LE = 1 cm.

f4( xs)
2 1 0 1 2 3 4 5
{ 1
4 x2
1
16
− x für x > 0
x4 − 2x für x ≤ 0
g: x--> Dg = R
6 1.8.1 Weisen Sie nach, dass die Funktion g an der Nahtstelle stetig ist. Untersuchen Sie anschließend
rechnersisch, ob der Graph von g an dieser Stelle "ohne Knick" verläuft.
Stetigkeit: x0 = 0 (1) g( x0)
= 0 1P
8
7
6
5
4
3
2
1
1
2
3
4
3 1.7 Die Funktion F mit D F = R ist eine Stammfunktion von f 4 .
Untersuchen Sie F auf Wendestellen, ohne F(x) zu berechnen.
(2) LS
(3) RS
xs
1
0 h
h 0 16 −
lim ( )4 −
→
2( 0 − h)
1
0 h
h 0 4 +
lim ( )2 − 0 + h
→
→ 0 1P
xw := −2 .. 4
xw
→ 0 => g ist stetig bei x0=0 1P
-2
-1
0
1
2
3
4
= f4( xw)
5
2.063
0
-1.938
-3
-0.938
F´´ ( x)
= f´ 4 ( x)
x = 2 aus 1.4 Es ist ein Wendepunkt, weil bei f4 an dieser Stelle ein Extrempunkt ist. 3P
1.8 Gegeben ist nun die abschnittsweise definierte Funktion
8
=
1P
+
4P

h 0
1
0 h
16 −
Differenzierbarkeit
(2) LS lim
→
( )4 − 2( 0 − h)
− 0
−h
(2) RS
4
1.8.2 Zeichnen Sie den Graphen der Funktion g für −2 ≤ x ≤ 5 mit Farbe in das vorhandene
Koordinatensystem ein.
f4( xs)
f4( xg1)
+ 0.1
g( xg2)
lim
h → 0
1
0 h
4 + ( )2 − 0 + h − 0
h
8
7
6
5
4
3
2
1
2 1 0 1 2 3 4 5
1
2
3
4
→ 1
→ −2
1P
xs , xg1 , xg2
1P
=> g ist nicht diffbar bei x0=0
xw := 0 .. 5
xw =
0
1
2
3
4
5
1P
+
3P
1P
g( xw)
0
-0.75
-1
-0.75
0
1.25
=

6
1.9 Zwischen den Graphen G f4 , G g , der Geraden x = 2 und dem Koordinatenursprung liegt im
4. Quadranten ein Flächenstück. Schraffieren Sie dieses Flächenstück und berechnen Sie die
Maßzahl des Flächeninhalts.
xm := 0 , 0.17 .. 2
2
⌠
A := ⎮ g( x)
− f4( x)
dx
⌡
0
⌠
⎮
S( x)
:= g( x)
− f4( x)
dx
→
⎮
⌡
2.0 Nebenstehende Skizze zeigt den Querschnitt einer überdachten Wasserrutsche. Der Graph G w
stellt die Wasserrutsche, der Graph G b stellt die Bedachung dar, die über die Rutsche hinaus
1
30 x2 35
36 x − 10 +
b: x->
D 1
x
100
w = [ 0; 10]
3
15x 2
verlängert ist. Die Funktionen w und b sind geben durch
w: x-> ⋅ ( − + 500)
w ( xw)
b( xb)
11
10
9
8
7
6
5
4
3
2
1
f4( xs)
g( xg2)
f4( xm)
g( xm)
2P
1
12 x3 ⋅
+
2 0 2 4
1
34
A →
15
1
2 x2
1
⋅
80 x5 − ⋅
1P
8
7
6
5
4
3
2
1
2
3
4
A = 2.267
1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1
xw , xb
2
xs , xg2 , xm , xm
S( 0)
→ 0
S( 2)
1P
→
34
15
1P
1P
1P
D b = [ 0; 15]

4 2.1 Berechnen Sie, an welcher Stelle x1 die Wasserrutsche das stärkste Gefälle aufweist.
Gesucht ist das (absolute) Minimum der 1. Ableitung (Gefälle)
wa( x)
2.3 Die Funktion d: x-> d(x) mit D d = [ 0; 10] beschreibt den in y-Richtung gemessenen Abstand
zwischen Wasserrutsche und Dach. Zeigen Sie, dass sich d(x) auch in der Form
1
d( x)
− x
100
3 11
⋅
60 x2
35
+
36 x − 5 +
:= schreiben lässt.
d( x)
= b( x)
− w( x)
1P
11
60 x2
35
⋅
36 x ⋅
1
− 5
100 x3
→ + − ⋅ 1P
8 2.4 Aus Sicherheitsgründen wird ein in y-Richtung gemessenen Mindestabstand zwischen
Wasserrutsche und Dach von 3,30 (LE) vorgegeben. Untersuchen Sie rechnerisch, ob dieser
Mindestabstand an jeder Stelle eingehalten wird.
da( x)
d 11
d( x)
dx
30 x ⋅
35 3
−
36 100 x2
11
:= →
− ⋅ 1P da( x)
= 0
30 x ⋅
35 3
−
36 100 x2
→ − ⋅ = 0 1P
2
⎛ 11⎞
⎛ −3
⎞ ⎛ 35⎞
4
D := ⎜ ⎟ − 4 ⋅ ⎜ ⎟ ⋅ ⎜−
⎟ →
30 100 36 225
xr := da( x)
= 0 auflösen, x
35
⎜ 9
→
25
xr =
⎝
daa( x)
d( xr0) ⎠
⎝
⎠
⎝
d
11 3
da( x)
dx
30 50 x ⋅ − →
:= daa( xr)
→
9925
→ d xr0 2916
⎠
( ) 3.404
= > 3.3 1P
⎛
⎜
⎜
⎜
⎜
⎝
2
15
−2
15
⎞ ⎟⎟⎟⎟⎠
=> Min 1P
=> Max
Ränder: d( 0)
= 5 d( 10)
= 3.611 => Der Mindestabstand wird an jeder Stelle eingehalten. 1P
60
d
3
w( x)
dx
100 x2
3
⋅
10 x ⋅ −
→
d
3
:= 1P waa( x)
wa( x)
dx
50 x ⋅
3
:= → − 1P
10
waa( x)
= 0 auflösen, x → 5 1P waaa( x)
Ränder: waa( 0)
= −0.3
und waa( 10)
= 0.3
=> bei x1 = 5 ist das Gefälle am stärksten.
1P
1P
d
3
:= waa( x)
→ >0 => Min
dx
50
4 2.2 Kondenswasser, das sich an der Unterseite der Bedachung gebildet hat, tropft von der tiefsten
Stelle des Daches herunter. Berechnen Sie die Stelle x2, an der das Wasser heruntertropft.
ba( x)
baa( x)
d 1
b( x)
dx
15 x ⋅
35
175
:= → − 1P x2 := ba( x)
= 0 auflösen, x → 1P x2 = 14.583
36
12
d
1
:= ba( x)
→ >0 => Min b( x2)
= 2.911
dx
15
Rechter Rand: b( 15)
= 2.917 => Das Wasser tropft bei 14.6 von der Decke
2
⎛
⎜
⎜
⎜
⎝
3
⎞ ⎟⎟⎟⎟⎠
⎛
⎜
⎝
3.889
8.333
2P
⎞
⎟
⎠

f( a , x)
:=
1
4a x4
− 2x

1
xg1 := −2 , −1.99
.. 0 xg2 := 0 , 0.01 .. 5 g( x)
4 x2 :=
− x

xw := 0 , 0.1 .. 10
xb := 0 , 0.1 .. 15
w( x)
( )
1
x
100
3
15x 2
1
:= ⋅ − + 500 b( x)
30 x2 35
36 x − 10 +
:=