1.6. Die lineare Funktion Einführendes Beispiel: Taxitarife in ...
1.6. Die lineare Funktion Einführendes Beispiel: Taxitarife in ...
1.6. Die lineare Funktion Einführendes Beispiel: Taxitarife in ...
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
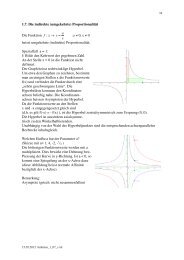
<strong>1.6.</strong> <strong>Die</strong> <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong><br />
<strong>E<strong>in</strong>führendes</strong> <strong>Beispiel</strong>:<br />
<strong>Taxitarife</strong> <strong>in</strong> Schweizer Städten s<strong>in</strong>d wie folgt aufgebaut:<br />
Für Fahrten ist e<strong>in</strong>e Grundgebühr von Fr. 7.- und zusätzlich pro gefahrenen Kilometer pro km<br />
Fr. 3.40 zu bezahlen.<br />
<strong>Die</strong> Kosten y (<strong>in</strong> Fr.) für e<strong>in</strong>e Fahrt von x (<strong>in</strong> km) s<strong>in</strong>d e<strong>in</strong>e <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> der Fahrtlänge:<br />
f: x → y = 3.40⋅x + 7<br />
Allgeme<strong>in</strong> :<br />
<strong>Die</strong> <strong>Funktion</strong> f: x → y = m⋅x + q m, q ∈ R heisst <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong>.<br />
<strong>Die</strong> <strong>Funktion</strong>svorschrift f bedeutet: Multipliziere die gegebene Zahl mit m und addiere q.<br />
<strong>Die</strong> direkte Proportionalität ist e<strong>in</strong> Spezialfall der <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong> (q = 0).<br />
Bei vielen Tarifen s<strong>in</strong>d die Kosten e<strong>in</strong>e <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> des Verbrauchs.<br />
<strong>Beispiel</strong>e von <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong>en<br />
a)<br />
E<strong>in</strong>e Helikopterfirma verlangt für Materialtransporte e<strong>in</strong>e Grundgebühr von Fr. 120.- und pro<br />
Flugm<strong>in</strong>ute Fr. 38.-<br />
<strong>Die</strong> Kosten y (<strong>in</strong> Fr.) für e<strong>in</strong>en Flug von x (<strong>in</strong> M<strong>in</strong>uten) s<strong>in</strong>d e<strong>in</strong>e <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> der<br />
Flugzeit:<br />
f : x → y = 38 ⋅ x + 120<br />
b)<br />
Wer e<strong>in</strong> Buch drucken lässt, bezahlt e<strong>in</strong>e Grundgebühr von Fr. 510.- und pro Exemplar<br />
Fr. 12.-.<br />
<strong>Die</strong> Herstellungskosten y s<strong>in</strong>d e<strong>in</strong>e <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> der Auflage x.<br />
f : x → y = 12 ⋅ x + 510<br />
c)<br />
In e<strong>in</strong>em gleichschenkligen Dreieck ist die Grösse des Basisw<strong>in</strong>kels y e<strong>in</strong>e <strong>Funktion</strong> des<br />
W<strong>in</strong>kels an der Spitze x.<br />
1<br />
f : x y = 90 − ⋅ x<br />
→ 2<br />
d)<br />
E<strong>in</strong> Behälter enthält 20 l Wasser, um 12 Uhr wird die Pumpe e<strong>in</strong>geschaltet, die <strong>in</strong> zwei<br />
Sekunden e<strong>in</strong>en Liter Wasser absaugt. Wie gross ist die Wassermenge y (<strong>in</strong> Liter), die sich<br />
t Sekunden nach 12 Uhr im Behälter bef<strong>in</strong>det?<br />
1<br />
f : x y = 20 − ⋅ x<br />
→ 2<br />
Bemerkung:<br />
Verdoppelt man x, so verdoppelt sich bei e<strong>in</strong>er Proportionalität auch der <strong>Funktion</strong>swert y,<br />
bei e<strong>in</strong>er <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong> gilt dies aber nicht.<br />
24.04.2012 funktion_1_06_s /ul<br />
18
Aufgabe:<br />
Zeichne den Graphen der <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong> f : x → y = m ⋅ x + q für die folgenden Parameter:<br />
m = 1 /2, q = 1, -2, 0.<br />
x -2 ⎯ ⎯→<br />
+1<br />
-1 ⎯ ⎯→<br />
+1<br />
0 ⎯ ⎯→<br />
+1<br />
1 ⎯ ⎯→<br />
+1<br />
2 ⎯ ⎯→<br />
+1<br />
3<br />
y -2m + q ⎯ ⎯→<br />
+m<br />
-m + q ⎯ ⎯→<br />
+m<br />
q ⎯ ⎯→<br />
+m m + q ⎯ ⎯→<br />
+m<br />
2m + q ⎯ ⎯→<br />
+m<br />
3m + q<br />
<strong>Die</strong> Wertetabelle zeigt, wenn x um 1 wächst, so verändert sich y gerade um m.<br />
Satz:<br />
Der Graph der <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong> f : x → y = m ⋅ x + q m, q ∈ R ist e<strong>in</strong>e Gerade mit der<br />
Steigung m durch den Punkt (0, q), q heisst y-Achsenabschnitt der Geraden. <strong>Die</strong> Gerade geht<br />
aus der Geraden mit der Gleichung y = mx durch e<strong>in</strong>e Translation <strong>in</strong> y-Richtung um q<br />
E<strong>in</strong>heiten hervor.<br />
24.04.2012 funktion_1_06_s /ul<br />
19
Aufgabe:<br />
2 Gegeben ist die <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> f : x → y = − 3 ⋅ x + 3<br />
a) Zeichne den Graphen der <strong>Funktion</strong><br />
b) Bestimme f(3)<br />
c) Bestimme x, so dass gilt: f(x) = -5 bzw. f(x) = 0 und <strong>in</strong>terpretiere diese Aussagen<br />
geometrisch.<br />
a)<br />
Der Graph ist e<strong>in</strong>e Gerade. Aus der <strong>Funktion</strong>sgleichung<br />
können die Steigung m = - 2 /3 und der<br />
y-Achsenabschnitt q = 3 herausgelesen werden.<br />
Steigung m bedeutet: wenn x um 3 zunimmt,<br />
dann nimmt y um 2 ab.<br />
Variante:<br />
Der Graph kann auch mit Hilfe zweier<br />
geeigneter Punkte z.B. A(-6, 4) und B(0, 3)<br />
gezeichnet werden.<br />
b)<br />
f(3) = 1 erhält man durch E<strong>in</strong>setzen <strong>in</strong> die <strong>Funktion</strong>sgleichung, der zugehörige Geradenpunkt<br />
A hat also die Koord<strong>in</strong>aten A(3, 1)<br />
c)<br />
Löse die Gleichung y = - 2 /3 x + 3 für y = -5 bzw. y = 0 nach x auf. Der ersten Lösung<br />
entspricht der Geradenpunkt B(12, -5), der zweiten der Schnittpunkt S( 9 /2 , 0) der Geraden mit<br />
der x-Achse.<br />
24.04.2012 funktion_1_06_s /ul<br />
20
Explizite, implizite Form der Geradengleichung<br />
Umgekehrt kann jede Gerade, die nicht zur y-Achse parallel ist, als Graph e<strong>in</strong>er <strong>l<strong>in</strong>eare</strong>n<br />
<strong>Funktion</strong> aufgefasst werden, das heisst die Gerade kann durch e<strong>in</strong>e Gleichung der Form<br />
y = mx + q dargestellt werden.<br />
Aufgabe:<br />
Bestimme e<strong>in</strong>e Gleichung der folgenden Geraden, wenn zwei Punkte gegeben s<strong>in</strong>d:<br />
a) A(0, 1), B(1, 4) b) A(0, -2) B(1, -3)<br />
a)<br />
Der y-Achsenabschnitt q = 1 ist gegeben.<br />
Vergrössert man x um 1, so nimmt y um 3 zu.<br />
<strong>Die</strong> Steigung der Geraden ist also m = 3<br />
Geradengleichung: y = 3x + 1<br />
Lösungsvariante:<br />
<strong>Die</strong> Gleichung der Geraden kann <strong>in</strong> der Form<br />
y = mx + 1 angesetzt werden. <strong>Die</strong> Koord<strong>in</strong>aten<br />
von B erfüllen diese Geradengleichung:<br />
4 = m⋅1 + 1 also ist m = 3.<br />
b) analog erhält man y = - x - 2<br />
c) A(0, 4) B(3, 0) d) A(0, 1) B(4,6)<br />
c)<br />
Vergrössert man x um 3, so nimmt y um 4 ab.<br />
Vergrössert man x um 1, so nimmt y um 4 /3 ab.<br />
<strong>Die</strong> Steigung der Geraden ist also a = - 4 /3.<br />
g: y = - 4 /3 x + 4<br />
5 d) analog g: y = ⋅ x + 1<br />
24.04.2012 funktion_1_06_s /ul<br />
4<br />
Übungsaufgaben:<br />
<strong>Die</strong> folgenden Geraden s<strong>in</strong>d durch zwei Punkte gegeben. Bestimme ihre Gleichung<br />
a) A(0, 3), B(1, 5) Lösung: y = 2 ⋅ x + 3 y = 2x + 3<br />
b) A(0, 2), B(1, 5) Lösung: y = 3 ⋅ x + 2 y = 3x + 2<br />
c) A(3, 0), B(2, 2) 1 3<br />
Lösung: y = − 2 ⋅ x + 2<br />
d) A(0, - 5 /3), B(1, - 1 /3) 4 5<br />
Lösung: y<br />
= 3 ⋅ x − 3<br />
21
Häufig kennt man von e<strong>in</strong>er Geraden zwei beliebige Punkte<br />
<strong>Beispiel</strong>: A(2, 1) B(6, 4)<br />
1. Lösungsweg:<br />
Wächst x um 4, so verändert sich y um 3<br />
Wächst x um 1, so wächst y um 3 /4<br />
also ist m = 3 /4.<br />
<strong>Die</strong> Gleichung der Geraden lässt sich damit <strong>in</strong><br />
der folgenden Form ansetzen:<br />
3 y = 4 ⋅ x + q<br />
q ist so zu bestimmen, dass die Koord<strong>in</strong>aten von<br />
A (oder B) die Geradengleichung erfüllen.<br />
y = x<br />
3<br />
4 ⋅ −<br />
1<br />
2<br />
2. Lösungsweg:<br />
<strong>Die</strong> Koord<strong>in</strong>aten von A und B erfüllen die Geradengleichung<br />
A(2, 1) 1 = 2m + q<br />
B(6, 4) 4 = 6m + q<br />
Drücke mit der 1. Gleichung q <strong>in</strong> m aus: q = 1 – 2m<br />
und setze den Term <strong>in</strong> die 2. Gleichung e<strong>in</strong>: 4 = 6m + 1 – 2m oder also m = 3 /4-.<br />
Allgeme<strong>in</strong>:<br />
A(xA, yA) erfüllt die Geradengleichung: yA = mxA + q<br />
B(xB, yB) erfüllt die Geradengleichung: yB = mxB + q<br />
Subtrahiert man die erste von der zweiten Gleichung so erhält man:<br />
yB − y A = m ⋅ ( xB<br />
− x A ) und daraus<br />
yB<br />
− y A ∆y<br />
m = =<br />
x − x ∆x<br />
B<br />
A<br />
Steigung e<strong>in</strong>er Geraden durch die Punkte A und B (A ≠ B)<br />
<strong>Beispiel</strong>:<br />
Gleichung der Geraden durch die Punkte A(3, -2) B(-4, 3)<br />
3 − ( −2)<br />
5<br />
m = = −<br />
− 4 − 3 7<br />
<strong>Die</strong> Gleichung de Geraden ergibt sich damit zu:<br />
5 y<br />
= − ⋅ x +<br />
7<br />
1<br />
7<br />
24.04.2012 funktion_1_06_s /ul<br />
22
5 1<br />
Im <strong>Beispiel</strong> wurde die Gleichung <strong>in</strong> der Form y = − 7 ⋅ x + 7 angegeben. <strong>Die</strong>se Gleichung der<br />
Form<br />
y = mx + q heisst explizite Form der Geradengleichung.<br />
Oft br<strong>in</strong>gt man diese Gleichung auf die Form 5x + 7y - 1 = 0 . <strong>Die</strong>se Gleichung der Form<br />
ax + by + c = 0 heisst implizite Form der Geradengleichung.<br />
Nachteil:<br />
<strong>Die</strong> Steigung und der y-Achsenabschnitt lassen sich nicht mehr direkt angeben.<br />
Vorteil:<br />
Jede Gerade der Ebene (auch e<strong>in</strong>e Parallele zur y-Achse) lässt sich durch e<strong>in</strong>e Gleichung<br />
dieser Form darstellen.<br />
Ist nämlich e<strong>in</strong>e Gerade parallel zur y-Achse, dann hat die x-Koord<strong>in</strong>ate e<strong>in</strong>en festen Wert, die<br />
y-Koord<strong>in</strong>ate h<strong>in</strong>gegen ist beliebig. In diesem Fall ist y ke<strong>in</strong>e <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> von x. <strong>Die</strong><br />
Gleichung e<strong>in</strong>er Parallelen zur y-Achse hat die Form x = c.<br />
Es gilt der folgende<br />
Satz:<br />
Jede Gerade der Ebene lässt sich durch e<strong>in</strong>e Gleichung der Form ax + by + c = 0<br />
mit a, b, c ∈ R darstellen, wobei a und b nicht beide 0 se<strong>in</strong> dürfen (so genannte implizite Form<br />
der Geradengleichung).<br />
Beweis:<br />
1. Fall: Ist b = 0 dann kann die Gleichung durch a ≠ 0 dividiert werden<br />
c<br />
x = −<br />
a<br />
Gleichung e<strong>in</strong>er Parallelen zur y-Achse.<br />
2. Fall: Ist b ≠ 0 dann kann die Gleichung nach y aufgelöst werden<br />
a<br />
y<br />
b x<br />
c<br />
= − −<br />
b<br />
Gleichung e<strong>in</strong>er Geraden mit der<br />
a<br />
c<br />
Steigung m = − und dem y-Achsenabschnitt q = − .<br />
b<br />
b<br />
24.04.2012 funktion_1_06_s /ul<br />
23
Aufgabe:<br />
Gegeben ist die Gerade g: 3x - 4y - 12 = 0. (1)<br />
a)<br />
Bestimme die Steigung und die Achsenschnittpunkte von g und zeichne die Gerade.<br />
3 Führt man Gleichung (1) <strong>in</strong> die explizite Form y = 4 ⋅ x − 3 (2) über, dann können die<br />
Steigung m = 3 /4 und der y-Achsenabschnitt q = -3 direkt abgelesen werden.<br />
<strong>Die</strong> Koord<strong>in</strong>aten der Achsenschnittpunkte können auch direkt mit Gleichung (1) bestimmt<br />
werden:<br />
Für den Schnittpunkt mit der x-Achse gilt: y = 0 A(4, 0)<br />
Für den Schnittpunkt mit der y-Achse gilt: x = 0 B(0, -3).<br />
b)<br />
Welche Koord<strong>in</strong>aten hat der Geradenpunkt C mit der x-Koord<strong>in</strong>ate 100?<br />
aus (2) y = 72 oder C(100, 72)<br />
c)<br />
Wie heisst die Gleichung der Parallelen p zur Geraden g durch den Punkt D(8, 5)<br />
Da parallele Geraden die gleiche Steigung haben, kann p <strong>in</strong> der Form<br />
3 p: y = 4 ⋅ x + q angesetzt werden. q ist so zu wählen, dass die Koord<strong>in</strong>aten des Punktes<br />
D(8, 5) die Gleichung erfüllen: 5 = 3 /4 8 + q und damit q = -1.<br />
3 <strong>Die</strong> Parallele hat also die Gleichung p: y = y = ⋅ x −1<br />
d)<br />
Welche Koord<strong>in</strong>aten hat der Schnittpunkt S von g mit der 1. W<strong>in</strong>kelhalbierenden?<br />
Für e<strong>in</strong>en Punkt der 1. W<strong>in</strong>kelhalbierenden stimmen x- und y-Koord<strong>in</strong>ate übere<strong>in</strong>.<br />
(1) liefert die Koord<strong>in</strong>aten des Schnittpunkts S(-12, -12).<br />
Spezialfälle:<br />
Bestimme e<strong>in</strong>e Gleichung der folgenden Geraden<br />
a)<br />
Parallele zur x-Achse durch den Punkt A(3, 2) y = 2 Gleichung der x-Achse y = 0<br />
b)<br />
Parallele zur y-Achse durch den Punkt B(-3, -4) x = -3 Gleichung der y-Achse x = 0<br />
Zusammenfassung:<br />
Jede Gerade, die nicht zur y-Achse parallel ist, kann durch e<strong>in</strong>e Gleichung der Form<br />
y = mx + q dargestellt werden (explizite Form der Geradengleichung).<br />
Jede Gleichung der Form ax + by + c = 0 mit a 2 + b 2 ≠ 0 (es dürfen nicht beide Koeffizienten<br />
gleich 0 se<strong>in</strong>) stellt e<strong>in</strong>e Gerade dar (implizite Form der Geradengleichung).<br />
24.04.2012 funktion_1_06_s /ul<br />
4<br />
24
Übungsaufgaben:<br />
a)<br />
<strong>Die</strong> Gerade g mit der Steigung m = -2 geht durch den Punkt P(3, -4). Wie heisst ihre<br />
Gleichung?<br />
Lösung:<br />
Ansatz: g: y = -2x + b P(3, -2) erfüllt die Geradengleichung g: y = -2x + 4<br />
b)<br />
Bestimme e<strong>in</strong>e Gleichung der Parallelen p zur Geraden g = A(20, 32), B(18, 29) durch den<br />
Punkt C(100, 200)<br />
3 Lösung: y = − ⋅ x + 50<br />
24.04.2012 funktion_1_06_s /ul<br />
2<br />
c):<br />
Berechne den Inhalt des abgebildeten Dreiecks DGH<br />
CD : y = x<br />
GH:<br />
G:<br />
H:<br />
1<br />
2<br />
5<br />
2<br />
y = x + 3<br />
3 15<br />
y = x + 3 = x x = y =<br />
1<br />
5<br />
2 2<br />
H H<br />
1<br />
2 H<br />
G 2 G 4<br />
x = 4, y = x + 3 = 5<br />
Dreieckshöhe: h = xH Basis DH = 5,<br />
Flächen<strong>in</strong>halt:<br />
− xG<br />
5 = 2 ,<br />
25<br />
4<br />
25
Senkrecht aufe<strong>in</strong>ander stehende Geraden<br />
Satz:<br />
Stehen die Geraden g und g‘ mit den Steigungen m und m‘ aufe<strong>in</strong>ander senkrecht, dann gilt:<br />
m⋅m‘ = -1<br />
Skizze:<br />
m = 1 /2 , m‘ = -2<br />
Der Punkt (1, m) geht bei e<strong>in</strong>er Drehung um<br />
90°, <strong>in</strong> den Punkt (-m, 1) über. Damit hat die<br />
1<br />
Gerade g‘ die Steigung m′<br />
= − .<br />
m<br />
Aufgabe:<br />
Welcher Punkt der x-Achse hat von den Punkten A(0, 0) und B(4, 8) den gleichen Abstand?<br />
Koord<strong>in</strong>aten des Mittelpunkts M der Geraden AB: M(2, 4)<br />
Steigung m der Geraden AB: m = 2<br />
Steigung der Mittelsenkrechten von AB: m‘ = - 1 /2<br />
Ansatz für die Gleichung der Mittelsenkrechten y = - 1 /2 x + q<br />
<strong>Die</strong> Koord<strong>in</strong>aten von M erfüllen die<br />
Gleichung: 4 = - 1 /2 ⋅2 + q q = 5<br />
Schnittpunkt mit der x-Achse y = 0 = - 1 /2 x + 5 x = 10<br />
geometrisch: Z(10, 0) ist Mittelpunkt e<strong>in</strong>es Kreises durch die Punkte A und B.<br />
24.04.2012 funktion_1_06_s /ul<br />
26
Übungsaufgabe:<br />
<strong>Die</strong> Gerade g: 3x - 4y - 25 = 0 ist Tangente e<strong>in</strong>es Kreises mit Mittelpunkt M(4, 3). Bestimme<br />
den Berührungspunkt B der Tangente mit dem Kreis.<br />
Lösung: B(7, -1)<br />
<strong>Die</strong> Aufgabe, den Umkreismittelpunkt e<strong>in</strong>es Dreiecks zu bestimmen, kann damit gelöst<br />
werden, <strong>in</strong>dem man zwei Mittelsenkrechte schneidet.<br />
<strong>Beispiel</strong>: Umkreismittelpunkts M des Dreiecks A(6, -7), B(-8, -7), C(4, 5)<br />
Lösungsidee:<br />
M ist Schnittpunkt der Mittelsenkrechten der Strecke AB bzw. AC<br />
Lösung M(-1, -2), Umkreisradius: r = MA = 74<br />
24.04.2012 funktion_1_06_s /ul<br />
27
L<strong>in</strong>eare <strong>Funktion</strong>en <strong>in</strong> Anwendungen<br />
<strong>Beispiel</strong>e:<br />
1.<br />
Bei e<strong>in</strong>er <strong>l<strong>in</strong>eare</strong>n Notenskala ist die Note y e<strong>in</strong>e <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> der Punktzahl x.<br />
In e<strong>in</strong>er schriftlichen Arbeit s<strong>in</strong>d maximal M = 13 Punkte zu erreichen. Für M = 13 Punkte<br />
gibt der Lehrer die Note 6, für 0 Punkte die Note 1. Welcher Zusammenhang besteht zwischen<br />
der Punktzahl x und der Note y?<br />
<strong>Die</strong> <strong>l<strong>in</strong>eare</strong> Notenskala ist durch die beiden Geradenpunkte A(0, 1) und B(M, 6) e<strong>in</strong>deutig<br />
festgelegt zu:<br />
5<br />
f : x → y = ⋅ x + 1<br />
M<br />
Im <strong>Beispiel</strong> bedeutet f: multipliziere die Punktzahl mit 5 /13 und addiere 1.<br />
Zusatzfragen:<br />
Welche Note erhält e<strong>in</strong> Schüler für die Punktzahl 9? f(9) = 4.46<br />
Für welche Punktzahl erhält man die Note 4? d.h. für welches x ist f(x) = 4?<br />
Gesucht ist die sogenannte Umkehrfunktion g von f<br />
5<br />
Dazu löst man die Gleichung y = ⋅ x + 1 nach x auf :<br />
M<br />
5<br />
M<br />
y −1<br />
= ⋅ x und nach Multiplikation mit M: x = ⋅ ( y −1)<br />
M<br />
5<br />
Mit der üblichen Variablenbezeichnung:<br />
M<br />
g : x → y = ⋅ ( x −1)<br />
5<br />
Im <strong>Beispiel</strong> bedeutet g: subtrahiere 1 und multipliziere mit 13 /5<br />
<strong>Die</strong> Note 4 erhält man damit für g(4) = 7.8 Punkte.<br />
24.04.2012 funktion_1_06_s /ul<br />
28
2.<br />
Temperaturskalen<br />
Gabriel Fahrenheit (1686-1736) baute 1714 e<strong>in</strong> Quecksilberthermometer und führte die nach<br />
ihm benannte Fahrenheit-Skala (°F) e<strong>in</strong>, die <strong>in</strong> Amerika und England heute noch gebräuchlich<br />
ist.<br />
1730 entwickelte der Franzose Seigneur de Réaumur (1683-1757) e<strong>in</strong> We<strong>in</strong>geistthermometer<br />
und führte die Réaumur-Skala (°R) e<strong>in</strong>.<br />
Der schwedische Astronom Anders Celsius (1701-1744) baute 1742 ebenfalls e<strong>in</strong><br />
Quecksilberthermometer mit der bei uns gebräuchlichen Celsius-Skala (°C).<br />
<strong>Die</strong> Physik verwendet wieder e<strong>in</strong>e andere Temperaturskala , die Kelv<strong>in</strong>-Skala (°K) oder<br />
absolute Temperatur, benannt nach dem Briten Lord Kelv<strong>in</strong> (1824-1907).<br />
Für den Gefrierpunkt und den Siedepunkt von Wasser gelten die folgenden Werte:<br />
Celsius Reaumur Fahrenheit Kelv<strong>in</strong><br />
Gefrierpunkt: 0 0 32 273.16<br />
Siedepunkt: 100 80 212 373.16<br />
Das Problem der Umrechnung von der Celsius- <strong>in</strong> die Fahrenheitskala bedeutet <strong>in</strong> die Sprache<br />
der Geometrie übersetzt, dass die Gleichung der Geraden durch die Punkte A(0,32) und<br />
B(100,212) gesucht ist. Ihre Steigung ergibt sich zu<br />
∆y<br />
180 9<br />
m = = = 5<br />
∆x<br />
100<br />
<strong>Die</strong> Umrechnung von der Celsius-Skala (x °C).<strong>in</strong> die Fahrenheit-Skala (y °F) wird also durch<br />
die folgende <strong>l<strong>in</strong>eare</strong> <strong>Funktion</strong> beschrieben:<br />
9<br />
f : x → y = ⋅ x + 32<br />
5<br />
Übungsaufgaben:<br />
a)<br />
Welche <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong>en beschreiben die Umrechnung von der Celsius-Skala (x °C).<strong>in</strong> die<br />
übrigen Skalen?<br />
C → K: f : x → y = x + 273.<br />
16<br />
K → C: f : x → y = x − 273.<br />
16<br />
4<br />
5<br />
C → R: f : x y = ⋅ x<br />
R → C: f : x y = ⋅ x<br />
→ 5<br />
24.04.2012 funktion_1_06_s /ul<br />
→ 4<br />
1 : x → y = 9 ⋅ ( 5x<br />
−<br />
F → C: f<br />
32)<br />
b)<br />
In New York sollen die Temperaturen im Juni zwischen 63 °F und 80 °F liegen. Welchem<br />
Intervall entsprechen diese Werte <strong>in</strong> der Celsius-Skala?<br />
Lösung: Zwischen 31.4°C und 40.9°C<br />
29
3.<br />
L<strong>in</strong>eare Interpolation<br />
In Anwendungen stellt sich oft das Problem, aus zwei Messpunkten oder Tabellenwerten<br />
e<strong>in</strong>en plausiblen Zwischenwert zu gew<strong>in</strong>nen. Wählt man diesen Zwischenwert so, dass die<br />
drei Punkte auf e<strong>in</strong>er Geraden liegen, so spricht man von <strong>l<strong>in</strong>eare</strong>r Interpolation.<br />
Gleichung der Interpolationsgeraden:<br />
yB − yA<br />
Steigung der Geraden AB; m =<br />
xB − xA<br />
<strong>Die</strong> Koord<strong>in</strong>aten des Punktes A erfüllen die<br />
Geradengleichung:<br />
yA = m ⋅ xA + q oder q = m⋅ xA − yA<br />
ergibt die Gleichung der Interpolationsgeraden:<br />
y − y<br />
y = y + ⋅ x − x<br />
( )<br />
B A<br />
A<br />
xB − xA<br />
A<br />
Setzt man <strong>in</strong> dieser Gleichung für d den Wert x0, so ergibt sich der plausible Zwischenwert y0.<br />
<strong>Beispiel</strong>e:<br />
a)<br />
Bei e<strong>in</strong>em Meilenrennen <strong>in</strong> der Leichtathletik wurden die beiden folgenden Zeiten gemessen:<br />
Schlusszeit nach 1609.344 m: 3’ 30.18’’<br />
Durchgangszeit bei 1200 m: 2’ 38.45’’<br />
Vermutete Zwischenzeit <strong>in</strong> s nach 1500 m:<br />
300<br />
158. 45 + ⋅51.<br />
73 = 196.36 s bzw. 3’ 16.36’’<br />
409.<br />
344<br />
b)<br />
Der Druck des gesättigten Wasserdampfs bei 40°C beträgt etwa 7.38 Kap und bei 50° etwa<br />
12.34 Kap. Bestimme mit <strong>l<strong>in</strong>eare</strong>r Interpolation e<strong>in</strong>en plausiblen Wert für den Druck bei<br />
43°C.<br />
12.<br />
34 − 7.<br />
38<br />
y = 7. 38 +<br />
⋅ ( 43 − 40)<br />
= 8.87 Kap<br />
50 − 40<br />
24.04.2012 funktion_1_06_s /ul<br />
30
4.<br />
Graphischer Fahrplan als Anwendung der <strong>l<strong>in</strong>eare</strong>n <strong>Funktion</strong> bei der gleichförmigen<br />
Bewegung.<br />
24.04.2012 funktion_1_06_s /ul<br />
31
5.<br />
L<strong>in</strong>eare Regression<br />
In Anwendungen stellt sich oft das Problem, gegebenen Messpunkten e<strong>in</strong>e bestmögliche<br />
Gerade anzupassen. <strong>Die</strong>s ist das Problem der sogenannten L<strong>in</strong>earen Regression, das später im<br />
Kapitel Analysis →Polynomfunktionen →Extremalprobleme →L<strong>in</strong>eare Regression<br />
rechnerisch gelöst wird.<br />
Im folgenden <strong>Beispiel</strong> wurde die Dehnung e<strong>in</strong>er elastischen Feder <strong>in</strong> cm <strong>in</strong> Abhängigkeit von<br />
der Masse m <strong>in</strong> kg gemessen mit den folgenden Ergebnissen:<br />
Masse m <strong>in</strong> kg 0 0.2 0.6 0.8<br />
Dehnung l <strong>in</strong> cm 28 36 53 61<br />
<strong>Die</strong> Ausgleichsgerade kann nun angenähert grafisch bestimmt werden, <strong>in</strong>dem man e<strong>in</strong>e<br />
Gerade möglichst gut vier gegebenen Messpunkten anpasst. <strong>Die</strong> Gleichung der Geraden kann<br />
etwa mit Hilfe zweier Punkte der Ausgleichsgeraden bestimmt werden.<br />
24.04.2012 funktion_1_06_s /ul<br />
32
Das folgende <strong>Beispiel</strong> stammt aus der F<strong>in</strong>anzmarkttheorie: Rendite von Wertpapieren<br />
(Quelle UBS)<br />
24.04.2012 funktion_1_06_s /ul<br />
33