Trigonometrie 1

Trigonometrie 1
1. Einleitung, Definition
Die Trigonometrie behandelt das Problem der Berechnung von Dreiecken. Es bestehen schöne
Anwendungen in der Vermessung oder Astronomie.
Aufgabe:
Zeichne ein rechtwinkliges Dreieck mit dem Winkel = 55 . Bestimme die Längen von
Ankathete, Gegenkathete und Hypotenuse und berechne die Näherungswerte der folgenden
Seitenverhältnisse Sinus (sin), Cosinus
(cos), Tangens (tan), Cotangens (cot)
sin
cos
tan
cot
a
c
b
c
a
b
b
a
Ankathete
Hypotenuse
22.02.2012 trigo_1/ul
Gegenkathete
Hypotenuse
Gegenkathete
Ankathete
Ankathete
Gegenkathete
Schülerinnen schlagen folgende Merkregel vor:
sin cos tan cot
G A G A
H H A G
Bemerkungen:
Da alle rechtwinkligen Dreiecke mit dem Winkel zueinander ähnlich sind, sind die Werte
der Seitenverhältnisse von der speziellen Wahl des Dreiecks unabhängig Die Werte der
Seitenverhältnisse hängen damit nur vom Winkel ab, sind eine Funktion des Winkels .
Ist umgekehrt ein Seitenverhältnis gegeben, so bestimmt dies den Winkel und damit auch
die übrigen Seitenverhältnisse eindeutig.
Zur Herkunft des Wortes Sinus:
Sehne heisst indisch jiva. Es wurde von den Arabern als Fremdwort übernommen. Da es
ähnlich tönt wie das arabische Wort für Ein-, Ausbuchtung führte dies zur falschen
Übersetzung ins Lateinische.
1

Aufgabe:
Zeichne ein rechtwinkliges Dreieck mit Winkel , so dass gilt sin = 4 /5 und gib die
restlichen Funktionswerte (ohne TR) an.
Wähle z.B. die Gegenkathete a = 8 und die
Hypotenuse c = 10. Für die Ankathete b gilt
dann nach Pythagoras b = 4. Damit können die
Funktionswerte angegeben werden:
cos = 4 /5, tan = 3 /4, cot = 4 /3.
Uebungsaufgabe:
geg. tan 8
ges. cos ohne TR
Lösung: cos = 1 /3
2. spezielle Winkel
Die trigonometrischen Funktionswerte sind i.a. irrationale Zahlen, für die der Taschenrechner
Näherungswerte liefert. Wie die folgenden Beispiele zeigen, können in einigen Fällen genaue
Werte angegeben werden.
a) = 45
Betrachte die Hälfte eines Einheitsquadrats
sin 45
cos45
22.02.2012 trigo_1/ul
1
2
2
tan 45
2
cot45
b) = 30 bzw. 60°
Betrachte die Hälfte eines gleichseitigen Dreiecks mit der
Seite 2 und der Höhe 3
1
sin 30 cos 60
sin 60 cos 30
2
1 3
tan 30 cot 60
tan 60 cot 30 3
3 3
Eselsleiter:
0° 30° 45° 60° 90°
sin
0
2
1
2
2
2
3
2
4
2
1
3
2
2

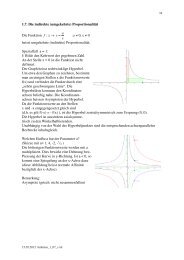
3. Folgerung aus der Definition
sin = cos (90° - ) z.B. sin 30° = cos 60°
cos = sin (90° - ) z.B. cos 50° = sin 40°
tan = cot (90° - ) z.B. tan 20° = cot 70°
cot = tan (90° - ) z.B. cot 40° = tan 50°
4. Darstellung der trigonometrischen Funktionswerte am Einheitskreis
Die trigonometrischen Funktionswerte erscheinen als Masszahlen der farbig bezeichneten
Strecken. Beachte OB = OC = OE = 1
sin
cos
tan
cot
AB
OB
OA
OB
AB
OA
OA
AB
AB y
OA x
22.02.2012 trigo_1/ul
CD
OC CD
EF
OE EF
Wächst von 0° bis 90°
- so wächst sin von 0 bis 1
- so fällt cos von 1 bis 0
- so wächst tan von 0 bis , d.h. nähert sich
der Winkel 90°, so wird tan grösser
als jede noch so grosse positive Zahl
- so fällt cot von bis 0.
Beachte:
Die Funktionswerte wachsen nicht linear.Insbesondere bedeutet eine Verdopplung des
Winkels nicht eine Verdopplung des Funktionswerts.
tan 90° bzw. cot 0° sind nicht definiert.
5. Grundlegende Beziehungen
Aus der Skizze ergeben sich die folgenden grundlegenden Beziehungen:
Pythagoras im Dreieck OAP:
( 1)
( 2)
( 3)
cos
tan
cot
2
sin
2
sin
cos
1
tan
1
cot
cos
sin
3

Bemerkungen:
2 2
cos cos cos (cos )
(1) drückt aus, dass sich cos in sin ausdrücken lässt
2
cos 1 sin
22.02.2012 trigo_1/ul
bzw. umgekehrt sin in cos
sin
1
2
cos
Die Beziehungen gelten für beliebige zulässige Winkel, d.h. kann z.B. ersetzt werden
durch 2 oder /2.
Die Funktionswerte sind aber nicht zum Winkel proportional d.h. sin (2 ) 2sin
Beispiele:
- Grundlegende Beziehungen anwenden
- Terme auf einen gemeinsamen Bruchstrich bringen
- ausklammern, faktorisieren
B: Vereinfache
2 2
sin cos sin 1 2 2 1
cos sin tan cos sin
cos cos cos cos
(sin cos )
cos
B: Vereinfache
4
sin
2
sin
4
cos
2
cos
4
s
2
s
4
c
2
c
2
( s
2 2
c ) ( s
2 2
s c
2
c ) 2
s
2
c 1
B: Beweise die folgenden Identitäten:
a) 1
2
tan
1
2
cos
b)
1 cot
2
1
2
sin
Es ist zu zeigen, dass für jeden zulässigen Winkel linke und rechte Seite übereinstimmen.
Zeige, dass sich z.B. die linke (kompliziertere Seite) in die rechte Seite überführen lässt.
a)
2 2 2 2
sin sin cos sin
L 1 1
R b) analog
2 2
cos cos cos
Uebungsaufgabe:
Beweise die folgenden Identitäten:
sin cos
2tan sin
a) tan
b)
2
1 sin
tan sin
2 2
2 2
2
4

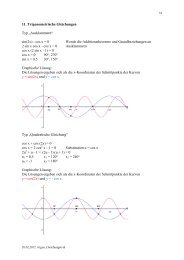
6. Bestimmung der trigonometrischen Funktionswerte mit der TR
a) Winkel gegeben, Funktionswert gesucht
Winkel im Gradmass (DEG! nicht GRAD!)
B: = 25° sin 25° = 0.4226 cos 25° = 0.9063
tan 25° = 0.4663 cot 25° = 2.1445 (Kehrwertfunktion!)
Winkel im Bogenmass (RAD)
B: = 1.309 sin 1.309 = 0.9659 cos 1.309 = 0.2588
tan 1.309 = 3.7321 cot 1.309 = 0.2679
Test mit sin 0.5
6
22.02.2012 trigo_1/ul
bzw. tan 1
4
b) Funktionswert gegeben, Winkel gesucht
Die Umkehrfunktion des Sinus heisst Arcussinus. Sie gibt zu einem bestimmten Sinuswert
den zugehören spitzen Winkel an (Bogen heisst auf lateinisch arcus).
Gradmass: sin = 0.8 = arcsin 0.8 = 23.6°
cos = 0.4 = arccos 0.4 = 66.4°
tan = 2 = arctan 2 = 63,4°
cot = 4 berechne zunächst tan = 0.25 (Kehrwertfunktion!)
und daraus = arctan 0.25 = 14.0°
Bogenmass sin = 0.8 = arcsin 0.8 = 0.9273
cos = 0.4 = arccos 0.4 = .1.1593
tan = 2 = arctan 2 = 1.1071
cot = 4 berechne zunächst tan = 0.25 (Kehrwertfunktion!)
und daraus = arctan 0.25 = 0.245
Zeige (ohne TR):
arctan(1) arctan(2) arctan(3) 180
= ?
5

7. Berechnung des rechtwinkligen Dreiecks
Eine Winkelfunktion verknüpft einen Winkel und zwei Seiten. Aus zwei der Grössen lässt
sich die dritte berechnen.
Grundaufgabe 1:
Berechne ein rechwinkliges Dreieck aus einem Winkel und der Hypothenuse
Gegeben: c,
= 90° -
a = c sin
b = c cos
numerische Beispiele:
= 29.6°, c = 23.9 = 60.4° a = 11.8 b = 20.8
= 19.4°, c = 7.63 = 70.6° a = 2.54 b = 7.20
Grundaufgabe 2:
Berechne ein rechwinkliges Dreieck aus einem Winkel und einer Kathete
Gegeben: a,
= 90° -
a
cos
c
tan
b
a
c
b
a
cos
a tan
numerisches Beispiel:
a = 31.7 = 58.0° = 32.0° c = 59.8 b = 50.7
22.02.2012 trigo_1/ul
6

Grundaufgabe 3:
Berechne ein rechtwinkliges Dreieck aus der Hypothenuse und einer Kathete
Gegeben: c, b
sin
b
c
arcsin
90
a
cos a c cos
c
22.02.2012 trigo_1/ul
b
c
numerisches Beispiel:
c = 13.6, b = 8.95 = 41.2° = 48.8° a = 10.24
Grundaufgabe 4:
Berechne ein rechwinkliges Dreieck aus den Katheten
Gegeben: a, b
tan
a
b
arctan
90
a
b
sin
a
c
c
a
sin
Höhe h: h b sin
Hypotenusenabschnitte:
p a cos q b cos
numerisches Beispiel:
a = 3.17, b = 5.08 = 32.0° = 58.0° c = 5.99
Aufgabe:
Von einem rechtwinkligen Dreieck ABC sind die Kathete a und die Hypotenuse c gegeben.
Berechne a) die Höhe hc b) die Winkelhalbierende w c) die Seitenhalbierende sb.
Lösung:
a) arccos a
c sin h a
b)
c)
90 b c cos w
b b
tan arctan
2a 2a
cos
a a
sb
s
cos
b
b
cos
2
7

Uebungsaufgaben:
a)
Von einem rechtwinkligen Dreieck kennt man die Hypotenuse c = 74.00 und die
Kathete a = 24.00. Berechne die Winkelhalbierende w .
Lösung: w = 70.97
b)
Die Fahrt mit der Seilbahn von die Talstation A zur Bergstation B dauert 16 Minuten. Diue
mittlere geschweindigkeit der Kabine beträgt 2 Meter pro Sekunde. Wir nehmen an, dass sich
die Kabine längs einer Geraden bewegt, die mit der Horintalen einen Winkel von 25° bildet.
Berechne auf Meter genau die Höhe der Bergstation B über der Talstation A.
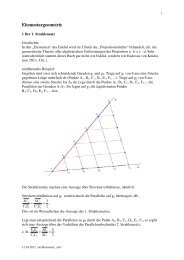
8. Berechnung von gleichschenkligen Dreiecken, Trapezen, regulären Vielecken
Gleichschenklige Dreiecke, Rechtecke, Rhomben, usw. können berechnet werden, indem man
geeignete rechtwinklige Teildreiecke betrachtet.
Aufgabe:
Berechne ein gleichschenkliges Dreieck aus der Basis c und der Höhe ha.
sin
cos
sin
180
ha
c
c
a
1
2
hc
a
2
h
c
2a
a
22.02.2012 trigo_1/ul
c
arcsin
a
sin
ha
c
c
2cos
1
2
c
tan
numerisches Beispiel:
c = 86.4, ha = 78.5
= = 65.3° = 49.4°
a = b = 103.4 hc = 94.0.
Ergänzung: Berechne den Inkreis- bzw. den Umkreisradius.
Aufgabe:
Im gleichseitigen Dreieck ABC mit der Seite
a = 6 wird die Seite AB durch die Teilpunkte
T1 und T2 in drei gleiche Teile zerlegt. Wel-
chen Winkel schliessen die Geraden CT1 und
CT2 ein?
Pythagoras:
h
tan 2
1
3 3
30 19.1
1
2
2 2
6 3 3 3
1
2arctan 21.8
3 3
8

Uebungsaufgaben:
a)
Bestimme in einem Rechteck mit den Seiten a = 28 und b = 45 den spitzen Schnittwinkel der
Diagonalen.
Lösung: 63.78°
b)
Wie gross sind die Innenwinkel eines Rhombus mit den Diagonalen e = 171.6 und f = 245.1
Lösung: 110.0°, 70.0°.
Aufgabe:
Berechne ein gleichschenkliges Trapez aus a, h und .
Geg. a, h, =
Ges. b = d , c Diagonale e = f
g = EB
h
b
sin
g h cot
c
a
2g
b
a
h
sin
2h
m
a b
2
Bestimmung der Diagonalen nach Pythagoras.
Variante: Hilfswinkel :
tan
h
a g arctan
h
a g sin
h
e
22.02.2012 trigo_1/ul
cot
numerisches Beispiel: a = 54.6 h = 9.86 = 65.5°
b = 10.8 c = 45.6 e = 11.1
e f
Kann keine direkte Beziehung zwischen bekannten Grössen und der gesuchten Grösse
aufgestellt werden, so führe man eine Hilfsvariable ein.
Eine einfache Vermessungsaufgabe:
Berechne die Höhe h eines Turmes , dessen
Fusspunkt unzugänglich ist.
geg: , , s Hilfsvariable BF = x
s x h cot x h cot eingesetzt
s h cot h cot
h
cot
s
cot
s tan
tan
tan
tan
num. B Kühlturm, Augenhöhe: 1.59 m, s = 80.00 m, = 13.13°, = 14.91°
Lösung: h = 152.5 m (incl. Augenhöhe)
h
sin
9

Uebungsaufgabe:
Der Beobachter B befindet sich a = 70 m über
dem Seespiegel. Er sieht die Bergspitze unter
dem Höhenwinkel = 28°, ihr Spiegelbild
unter einem Tiefenwinkel = 35°. Wie hoch
liegt S über dem Seespiegel?
Lösung:
Aufgabe:
Berechne den Flächeninhalt I eines spitzwinkligen Dreiecks aus zwei Seiten a,b und dem
eingeschlossenen Winkel
hb
sin hb
a sin
a
(1)
b hb
1 I ab sin
2
2
halbes Produkt der beiden Seiten mit
dem Sinus des eingeschlossenen Winkels.
numerisches Beispiel:
a = 8.0, b = 6.0, = 49.4° I = 18.2
Aufgabe:
Flächeninhalt eines gleichschenkligen Dreiecks mit Schenkel s und dem Winkel 2 zwischen
den beiden Schenkeln
einerseits nach (1)
2I s s sin( 2 )
andrerseits aus Grundlinie und Höhe
2I s s 2 sin cos
Daraus folgt die wichtige Formel:
sin(
2
)
2sin
22.02.2012 trigo_1/ul
cos
10

Die eben hergeleitete Formel ermöglicht es, den Sinuswert des doppelten Winkels zu
berechnen. Da für kleine Winkel der Sinus gut mit dem Bogenmass des entsprechenden
Winkels übereinstimmt gilt:
sin 1 0. 01745329252...
180
sin 2 2 1
0. 03490126806...
180 180
sin 4 0. 0676000998
22.02.2012 trigo_1/ul
2
In der Praxis verwendet man (möglichst rasch konvergierende) Reihen, z.B F u.T
Uebungsaufgabe:
Einem Kreis mit Radius r ist ein reguläres n-Eck a) einbeschrieben b) umbeschrieben.
Berechne die entsprechenden Flächeninhalte.
1 2 360
2 180
Ie 2 nr sin Iu nr tan
n
n
9. Aufgaben aus der Raumgeometrie
Räumliche Aufgaben können auf ebene zurückgeführt werden, indem man geeignete Schnitte
betrachtet.
Aufgabe:
Wie gross ist die Geschwindigkeit, mit der sich eine Erdbewohnerin im Punkt P mit der
geografischen Länge und der geografischen Breite um die Erdachse bewegt? (Die Erde
wird bei dieser Aufgabe als Kugel mit
dem Radius 6.37 10 3 km angenommen).
In der Skizze ist der Schnitt durch den
Längenkreis von P dargestellt. In 24
Stunden legt die Erdbewohnerin den
Umfang des Breitenkreises mit Radius
zurück:
Umfang des Breitenkreises:
U 2 2 R cos
Im Spezialfall Zofingen ( = 7.94383°
E) und = 47.28351°N legt die Bewohnerin
U 2 2 R cos 27151 km
in 24 3600 s zurück, bewegt sich also mit einer Geschwindigkeit von v = 314 m/s um die
Erdachse.
Zusatzfrage:
Auf welchem Breitenkreis könnte ein Flugzeug mit der Durchschnittsgeschwindigkeit von
300 km/h (in Oesterreich kmh genannt !?) in einem Tag gerade um die Erde fliegen?
Lösung: 2 R cos 24 300 = 79.6°
11

Uebungsaufgabe:
Der 47°-Breitenkreis geht durch Neuchâtel und Bad Ragaz. Berechne den sphärischen
Abstand der beiden Ortschaften aus ihren Längen 6°57’ und 9°30’.
Lösung:
Winkel bei regulären Polydern
Es kann bewiesen werden, dass es genau fünf reguläre Körper gibt. Euler hat den sogenannten
Eulerschen Polyedersatz bewiesen, der eine Aussage über die Beziehung zwischen der Anzahl
der Ecken e, der Anzahl der Flächen f und der Anzahl derkanten k macht:
e + f - k = 2 Eulersche Polyedersatz
1. Der Würfel (Hexaeder) e = 8 f = 6 k = 12
Berechne den Winkel zwischen der Raumdiagonale und einer Würfelkante.
Betrachte das rechtwinklige Dreieck aus einer Kante, einer Flächendiagonale und einer
Raumdiagonale arctan(
2)
54.
74
22.02.2012 trigo_1/ul
12

2. Das Tetraeder e = 4 f = 4 k = 6
Es wird von 4 gleichseitigen Dreiecken begrenzt. Das Tetraeder kann durch Verbinden
geeigneter Ecken eines Würfels dargestellt werden. Berechne
a) den Winkel zwischen einer Kante und einer Fläche
b) den Winkel zwischen zwei Flächen
In der Abbildung rechts ist der Grundriss des Tetraeders ABCD mit der Grundfläche ABC in
der xy-Ebene dargestellt. Legt man einen geeigneten Schnitt in die Grundebene um, so
entsteht das gleichschenklige Dreieck CED, wobei die Tetraederseite gleich der
Flächendiagonalen des links dargestellten Würfels ist. Wählen wir als Tetraederkante 2 dann
gilt für die
Höhe des gleichseitigen Dreiecks: h CE 3
Da die Höhe zugleich Seitenhalbierende ist verhalten sich die Höhenabschnitte wie 2: 1 d.h.
es gilt:
EF
3
3
CF
22.02.2012 trigo_1/ul
CF
2 3
3
3
cos
= 54.7°
CD 3
cos = 1 /3 und damit = arccos( 1 /3) 70.5°
bzw. = 180° - 2 .
3. Das reguläre Oktaeder e = 6 f = 8 k = 12
Es wird von acht gleichseitigen Dreiecken begrenzt.
Skizze:
Die Mitten der sechs Seitenflächen des Würfels bilden ein reguläres Oktaeder.
Halbiert man das Tetraeder so ist zu erkennen, dass sich
Gegenkathete und Ankathete des halben Winkels wie
die Diagonale und die Seite eines Quadrats verhalten.
Damit gilt für den gesuchten Winkel zwischen zwei
benachbarten Seitenflächen
2
arctan(
2)
109.
5
13

4. Das reguläre Dodekaeder 5. Das reguläre Ikosaeder
e = 20 f = 12 k = 30 e = 12 f = 20 k = 30
vgl. den Beitrag Auszug aus: Bilder der Mathematik Georg Glaeser, Konrad Polthier
http://www.symmetrie.info/downloads/begleittext_symmetrie_ausstellung.pdf
22.02.2012 trigo_1/ul
14

10. Beispiele aus der Physik
Aufgabe:
Zerlege den Kraftvektor F mit F = 7500 N in zwei Komponenten F1 und F2, die mit F die
Winkel 1 = 27.8° und 2 = 90° - 27.8°
einschliessen.
F1 = F cos 27.8° = 6634.4 N
F2 = F sin 27.8° = 3497.9 N
22.02.2012 trigo_1/ul
15

Aufgabe: Drei Gewichte
Ueber zwei Rollen in gleicher Höhe im Abstand von 4.7 dm wird eine Schnur gelegt, an deren
Enden je ein Gewicht mit der Gewichtskraft von 3 N bzw. 4 N hängt. Zwischen den beiden
Rollen ist an einem Knoten ein Gewicht mit einer Gewichtskraft von 3 N befestigt. Berechne
die Winkel, über welche die mittlere Masse im Gleichgewichtszustand mit den beiden Rollen
verbunden ist.
Versuchsanordnung: Markus Ninck, Foto: Rudolf Fischer 20.2.2012
Den drei Kräften entspricht das gleichschenklige Dreieck KLM mit der Basis KM. Im
rechtwinkligen Teildreieck gilt:
cos und daraus = 48.2° und schliesslich die gesuchten Winkel zu
2
3
= 6.4° und = 41.8°.
22.02.2012 trigo_1/ul
16

Aufgabe: Brechungsgesetz:
Ein Lichtstrahl, der auf die Grenzfläche von zwei optischen Medien trifft, wird gebrochen
oder reflektiert.
l Lichtstrahl
l’ gebrochener Lichtstrahl
e Einfallslot
Einfallswinkel
Brechungswinkel
Dabei gilt das Brechungsgesetz von Snellius:
1. l, l’ und e liegen in einer Ebene.
2. sin
n n heisst Brechungsindex
sin
Beim Übergang
von Luft in Wasser ist n = 4 /3
von Luft in gewöhnliches Glas ist n = 1.54
Uebungsaufgaben:
a)
Berechne für = 27° den Winkel beim Übergang von Luft in Wasser
Lösung: 20°
b)
Berechne für = 32.3° den zugehörigen Winkel wenn der Lichtstrahlvon Glas in die Luft
austritt. Bei welchem Winkel tritt Totalreflexion ein?
Lösung: = 54.3°, Totalreflexion bei 71.3°
22.02.2012 trigo_1/ul
17

Planparallele Glasplatten
Ein Lichtstrahl fällt mit dem Einfallswinkel auf
eine plane Glasplatte der Dicke d. Bestimme die
parallele Verschiebung v des ausfallenden Licht-
strahls zum einfallenden Strahl.
sin
sin
s d
n
tan
2 2
m s d
v m
sin
oder auch
v d
sin 1
1 sin n sin
22.02.2012 trigo_1/ul
n
cos
sin
2 2
18

11. Steigungswinkel einer Geraden
Der Winkel, den eine Gerade mit der
positiven x-Achse einschliesst, heisst
Steigungswinkel der Geraden.
Die Steigung m einer Geraden gibt die
Veränderung der y-Koordinate an, wenn
x um 1 wächst: m
22.02.2012 trigo_1/ul
y
x .
Satz:
m = tan
Die Steigung ist gleich dem Tangens des
Steigungswinkels
B:
3x - 2y + 2 = 0 implizite Form
y = 3 /2 x + 1 explizite Form
tan = 3 /2 = arctan( 3 /2 ) = 56.3°
B:
Die Polybahn überwindet auf 176 m Horizontaldistanz eine Höhendifferenz von 41 m.
Die Steigung beträgt m tan
41
176
0.23 also 23%, der Steigungswinkel beträgt
arctan
41
176
13.1
a% Steigung bedeutet a Meter Höhendifferenz auf 100 Meter Horizontaldistanz.
Steigung 100% bedeutet insbesondere Steigungswinkel 45°
Weitere Uebungsaufgaben z.B.
Erhard Rhyn:
Aufgabensammlung Trigonometrie und Vektorgeometrie mit Lösungen
rhyn.gut@balcab.ch
19