SMART Sammlung mathematischer Aufgaben als Hypertext mit TEX ...
SMART Sammlung mathematischer Aufgaben als Hypertext mit TEX ... SMART Sammlung mathematischer Aufgaben als Hypertext mit TEX ...
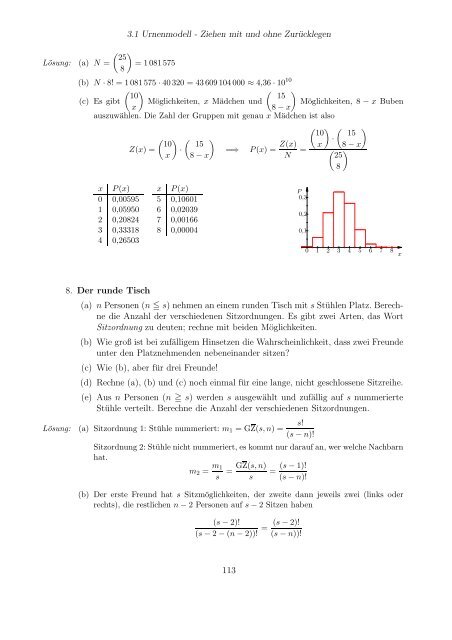
3.1 Urnenmodell - Ziehen mit und ohne Zurücklegen DaderTaschenrechnern!fürn > 69nichtberechnenkann,verwendenwirdasErgebnis in der Form (hier ist keine Fallunterscheidung nötig!) p(n) = 364 n−1 363 365−n+1 365−i · ·... = 365 365 365 365 i=1 n−1 p(n) = 1−p(n) = 1− i=1 365−i 365 Eine weiter Form für die Berechnung mit einem Taschenrechner, der die Binomialkoeffizienten beherrscht: 365! p(n) = 365n ·(365−n)! = 365!·n! 365n n! 365 = · ·(365−n)!·n! 365n n Weiter muss man aufpassen, dass der TR kein Zwischenergebnis ≧ 10100 errechnet. Als Beispiel die Berechnung für n = 40: 365 p(40) = · 39 326 40 : 36520 : 365 20 ·40! = 0,10877 =⇒ p(40) = 0,89123 Noch etwas trickreicher die Berechnung für n = 60: 365 = 60 365·364·...·327 · 1·2...·39 326·325·...·306 40·41...·60 p(60) = 365 : 60!· 39 ( 365 39) ( 326 21)· 21!·39! 60! 326 ·21!·39! : 365 21 20 : 365 20 : 365 20 ·60! = 0,005877 =⇒ p(60) = 0,99412 n 2 3 4 5 6 7 p(n) 0,274% 0,820% 1,64% 2,71% 4,05% 5,62% n 8 9 10 20 40 60 p(n) 7,43% 9,46% 11,69% 41,14% 89,12% 99,41% (b) p(22) = 47,57% und p(23) = 50,73% =⇒ ab 23 Personen 7. Eine Klasse mit 25 Schülern besuchen 15 Buben und zehn Mädchen. Für einen Wettbewerb wird eine Gruppe von acht Schülern der Klasse zufällig ausgewählt. (a) Berechne die Zahl N der verschiedenen möglichen Gruppen. (b) Wie viele verschiedene Gruppenfotos mit nebeneinander aufgestellten Schülern sind möglich, wenn man alle möglichen Gruppen berücksichtigt? (c) Wie viele verschiedene Gruppen mit genau x Mädchen und damit 8 − x Buben gibt es? Berechne die Wahrscheinlichkeit P(x), dass eine Gruppe genau x Mädchen enthält und stelle P(x) als Säulendiagramm grafisch dar. Wertetabelle nicht vergessen! 112
Lösung: (a) N = 3.1 Urnenmodell - Ziehen mit und ohne Zurücklegen 25 = 1081575 8 (b) N ·8! = 1081575 ·40320 = 43609104000 ≈ 4,36·10 10 10 15 (c) Es gibt Möglichkeiten, x Mädchen und Möglichkeiten, 8 − x Buben x 8−x auszuwählen. Die Zahl der Gruppen mit genau x Mädchen ist also 10 15 Z(x) = · =⇒ P(x) = x 8−x Z(x) N = 10 15 · x 8−x 25 8 x P(x) 0 0,00595 1 0,05950 2 0,20824 3 0,33318 4 0,26503 8. Der runde Tisch x P(x) 5 0,10601 6 0,02039 7 0,00166 8 0,00004 P 0,3 0,2 0,1 0 1 2 3 4 5 6 7 8 (a) n Personen (n ≦ s) nehmen aneinem runden Tisch mit s Stühlen Platz. Berechne die Anzahl der verschiedenen Sitzordnungen. Es gibt zwei Arten, das Wort Sitzordnung zu deuten; rechne mit beiden Möglichkeiten. (b) Wie groß ist bei zufälligem Hinsetzen die Wahrscheinlichkeit, dass zwei Freunde unter den Platznehmenden nebeneinander sitzen? (c) Wie (b), aber für drei Freunde! (d) Rechne (a), (b) und (c) noch einmal für eine lange, nicht geschlossene Sitzreihe. (e) Aus n Personen (n ≧ s) werden s ausgewählt und zufällig auf s nummerierte Stühle verteilt. Berechne die Anzahl der verschiedenen Sitzordnungen. Lösung: (a) Sitzordnung 1: Stühle nummeriert: m1 = GZ(s,n) = s! (s−n)! Sitzordnung2: Stühlenicht nummeriert, es kommtnurdaraufan, wer welche Nachbarn hat. m2 = m1 GZ(s,n) = = s s (s−1)! (s−n)! (b) Der erste Freund hat s Sitzmöglichkeiten, der zweite dann jeweils zwei (links oder rechts), die restlichen n−2 Personen auf s−2 Sitzen haben (s−2)! (s−2)! = (s−2−(n−2))! (s−n))! 113 x
- Seite 61 und 62: Lösung: (a) f(x) = (b) f ′ (x)dx
- Seite 63 und 64: lim = lim x→0 +g(x) x→0 + 2.6
- Seite 65 und 66: 6. Wir betrachten die Funktion f mi
- Seite 67 und 68: 2.6 Kurvendiskussion f ′′ (x22)
- Seite 69 und 70: 2.6 Kurvendiskussion f ′ (x) = 0
- Seite 71 und 72: 2.6 Kurvendiskussion auf Nullstelle
- Seite 73 und 74: 13. Gegeben ist die Funktion 2.6 Ku
- Seite 75 und 76: 2.6 Kurvendiskussion (b) Berechnen
- Seite 77 und 78: Lösung: 21. Wir betrachten die Fun
- Seite 79 und 80: (e) g ′ (x) = f′ (x) 2 f(x) (f
- Seite 81 und 82: 2.6 Kurvendiskussion 27. Wir betrac
- Seite 83 und 84: 2.6 Kurvendiskussion (d) Untersuche
- Seite 85 und 86: 2.6 Kurvendiskussion 33. Wir betrac
- Seite 87 und 88: 2.6 Kurvendiskussion (a) Berechne d
- Seite 89 und 90: 2.6 Kurvendiskussion (a) Untersuche
- Seite 91 und 92: 2.6 Kurvendiskussion Lösung: (a) f
- Seite 93 und 94: 2.6 Kurvendiskussion (b) Zeige, das
- Seite 95 und 96: 2.6 Kurvendiskussion (b) Geben Sie
- Seite 97 und 98: 2.6 Kurvendiskussion (b) Zeichnen S
- Seite 99 und 100: (d) 2.6 Kurvendiskussion a -5,0 -2,
- Seite 101 und 102: 2.6 Kurvendiskussion Neben Konstant
- Seite 103 und 104: Lösung: Lösung: 2.6 Kurvendiskuss
- Seite 105 und 106: 2.6 Kurvendiskussion (a) Untersuche
- Seite 107 und 108: 3 Stochastik: Binomialverteilung un
- Seite 109 und 110: 3.1 Urnenmodell - Ziehen mit und oh
- Seite 111: 3.1 Urnenmodell - Ziehen mit und oh
- Seite 115 und 116: 3.1 Urnenmodell - Ziehen mit und oh
- Seite 117 und 118: 3.1 Urnenmodell - Ziehen mit und oh
- Seite 119 und 120: 3.2 Bernoulli-Experiment und -Kette
- Seite 121 und 122: 3.3 Binomialkoeffizient, Binomialve
- Seite 123 und 124: (b) p2 = 20 p 15 15 q 5 = 3.3 Bin
- Seite 125 und 126: (f) 1−q n − 3.3 Binomialkoeffiz
- Seite 127 und 128: (b) p1 = p2 = (c) p3 = 70 k=0 500 k
- Seite 129 und 130: 4 Geometrie: Geraden und Ebenen im
- Seite 131 und 132: 4.1 Lineare Abhängigkeit von Vekto
- Seite 133 und 134: 4. Berechne die Lösungsmenge: 4.1
- Seite 135 und 136: 4.2 Geraden und Ebenen 4.2 Geraden
- Seite 137 und 138: ⎛ (c) h : −→ X = ⎝ -0,5 -2,
- Seite 139 und 140: 4.3 Gegenseitige Lage von Geraden u
- Seite 141 und 142: 4.3 Gegenseitige Lage von Geraden u
- Seite 143 und 144: 4.3 Gegenseitige Lage von Geraden u
- Seite 145 und 146: 4.3 Gegenseitige Lage von Geraden u
- Seite 147 und 148: 4.3 Gegenseitige Lage von Geraden u
- Seite 149 und 150: Lösung: (a) E1 : 4.3 Gegenseitige
- Seite 151 und 152: 4.3 Gegenseitige Lage von Geraden u
- Seite 153 und 154: 4.4 Abstand- und Winkelbestimmung P
- Seite 155 und 156: 4.4 Abstand- und Winkelbestimmung (
- Seite 157 und 158: 4.4 Abstand- und Winkelbestimmung (
- Seite 159 und 160: (d) Ph 4.4 Abstand- und Winkelbesti
- Seite 161 und 162: 4.4 Abstand- und Winkelbestimmung (
Lösung: (a) N =<br />
3.1 Urnenmodell - Ziehen <strong>mit</strong> und ohne Zurücklegen<br />
<br />
25<br />
= 1081575<br />
8<br />
(b) N ·8! = 1081575 ·40320 = 43609104000 ≈ 4,36·10 10<br />
<br />
<br />
10<br />
15<br />
(c) Es gibt Möglichkeiten, x Mädchen und Möglichkeiten, 8 − x Buben<br />
x<br />
8−x<br />
auszuwählen. Die Zahl der Gruppen <strong>mit</strong> genau x Mädchen ist <strong>als</strong>o<br />
<br />
10 15<br />
Z(x) = · =⇒ P(x) =<br />
x 8−x<br />
Z(x)<br />
N =<br />
<br />
10 15<br />
·<br />
x 8−x<br />
<br />
25<br />
8<br />
x P(x)<br />
0 0,00595<br />
1 0,05950<br />
2 0,20824<br />
3 0,33318<br />
4 0,26503<br />
8. Der runde Tisch<br />
x P(x)<br />
5 0,10601<br />
6 0,02039<br />
7 0,00166<br />
8 0,00004<br />
P<br />
0,3<br />
0,2<br />
0,1<br />
0 1 2 3 4 5 6 7 8<br />
(a) n Personen (n ≦ s) nehmen aneinem runden Tisch <strong>mit</strong> s Stühlen Platz. Berechne<br />
die Anzahl der verschiedenen Sitzordnungen. Es gibt zwei Arten, das Wort<br />
Sitzordnung zu deuten; rechne <strong>mit</strong> beiden Möglichkeiten.<br />
(b) Wie groß ist bei zufälligem Hinsetzen die Wahrscheinlichkeit, dass zwei Freunde<br />
unter den Platznehmenden nebeneinander sitzen?<br />
(c) Wie (b), aber für drei Freunde!<br />
(d) Rechne (a), (b) und (c) noch einmal für eine lange, nicht geschlossene Sitzreihe.<br />
(e) Aus n Personen (n ≧ s) werden s ausgewählt und zufällig auf s nummerierte<br />
Stühle verteilt. Berechne die Anzahl der verschiedenen Sitzordnungen.<br />
Lösung: (a) Sitzordnung 1: Stühle nummeriert: m1 = GZ(s,n) =<br />
s!<br />
(s−n)!<br />
Sitzordnung2: Stühlenicht nummeriert, es kommtnurdaraufan, wer welche Nachbarn<br />
hat.<br />
m2 = m1 GZ(s,n)<br />
= =<br />
s s<br />
(s−1)!<br />
(s−n)!<br />
(b) Der erste Freund hat s Sitzmöglichkeiten, der zweite dann jeweils zwei (links oder<br />
rechts), die restlichen n−2 Personen auf s−2 Sitzen haben<br />
(s−2)! (s−2)!<br />
=<br />
(s−2−(n−2))! (s−n))!<br />
113<br />
x