Kapitel 5

5 Wechselwegschaltung
Übungsziele:
• Schalten von Wechselspannungskreisen mit ohmscher Last und induktiver
Glättung
• Steuern von Wechselspannungskreisen mit ohmscher Last und induktiver Glä ttung
• Grenzfall rein ohmscher Last R
• Grenzfall bei idealem Speicher L
• Leistungsübertragung
• Grundschwingungsgehalt, Verschiebungs- und Leistungsfaktor
• Leistungsmittelwerte
Übungsdateien: MATHCAD: w1.mcd; w1s.mcd; 4fourier.mcd
SIMPLORER: w1rl.ssh; w1rl_m.ssh
5.1 Wechselstromschalter
Fügt man antiparallel zum M1-Einpulsgleichrichter ein zweites steuerbares Ventil
hinzu, liegt zusätzlich die negative Halbwelle der speisenden Spannung uS an der
Last an. Die Ausgangsspannung ist jetzt eine Wechselspannung, die allgemein als
Lastspannung uL bezeichnet wird. Bei der M1-Schaltung lag dagegen die Gleichspannung
ud an der Reihenschaltung aus Widerstand und induktivem Speicher.
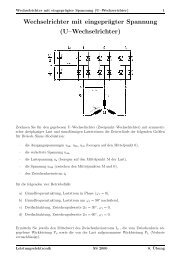
Bild 5.1: W1-Wechselschaltung
Das neue Netzwerk heißt jetzt Wechselwegschaltung W1. Durch die Steuerwinkel
α1 und α2, die gegeneinander um 180° elektrisch versetzt sind, werden die Ventile
gesteuert. Die Zündwinkel sind jeweils auf die positive und die negative Halb welle
der Eingangsspannung synchronisiert. Durch verzögertes Schalten gegenüber
dem Nulldurchgang der Spannungen kann die Lastspannung uL verändert werden.

5.1 Wechselstromschalter 69
Die Gleichung für den Ventilstrom iv folgt aus der Spannungsgleichgewichtsbedingung
entsprechend der Ventilstromberechnung der M1-Gleichrichterschaltung
im Definitionsbereich α ≤ x ≤ α+τd:
⎡
i ( x)
= Iˆ
⎢sin(
x −ϕ)
− sin(
α−ϕ)
e
⎢
⎣
⎤
⎥
⎥
⎦
x−α
−
ωτ
(5.1)
V
Beim Einschalten ohmsch-induktiver Kreise überlagert sich [s. Gleichung (5.1)]
einer Sinusfunktion mit der Phasenverschiebung ϕ = arctan (L/R) eine e-Funktion,
die mit der Zeitkonstanten τ = L/R des induktiven Spe ichers abklingt. Nicht nur in
der Stromrichtertechnik, sondern auch beim Schalten von Lasten mit starken induktivem
Anteil treten Stromüberhöhungen auf. Hohe Scheitelwerte des transienten
Stromes, also des vorübergehenden Stromanteils, können über seine Kraftwirkungen
unmittelbar die Leiterbahnen zerstören, falls sie nicht mechanisch entsprechend
stark ausgelegt sind. Eine zu hohe Wärmeentwicklung wird durch rechtzeitiges
Abschalten von Sicherungen meist rechtzeitig vermieden.
Die Wechselwegschaltung wird auch als elektronischer Schalter benutzt. Bei kleineren
Leistungen wird ein Triac als Chip mit integrierter Steuerschaltung verwendet.
Elektronische Schalter arbeiten verschleißfrei ohne mechanische Trägheit. Elektrische
Leitungen werden nicht galvanisch getrennt. Deswegen ist immer ein
zusätzlicher mechanischer Trennschalter aus Sicherheitsgründen erforderlich, wenn
an abgeschalteten Geräten gearbeitet wird.
u
i
ϕ
α
ie
uS
i0
iL
Bild 5.2: Einschaltvorgang

70
5 Wechselwegschaltung
Es wird ein Einschaltvorgang mit beiden Programmen simuliert. Die Eingabedaten
für MATHCAD und SIMPLORER sind R = 10 Ω und L = 100 mH. Die mathematische
Lösung zeigt Bild 5.2 in MATHCAD. Dort sind die Bestandteile der Gleichung
(5.1) separat gezeic hnet. Aus der Summe ergibt sich der einschwingende
Gesamtstrom, der nach einigen Perioden auf den Dauerstrom abgeklungen ist. Der
Einschaltzeitpunkt ist wesentlich für den maximalen Scheitelwert des Ein schaltstromes.
Bild 5.3 zeigt die Lösung im QuickView des SIMPLORERS. Bei allen Simulationsergebnissen
muss auf den Maßstab geachtet werden, da alle Simulationsergebnisse
nur gemeinsam in einer Grafik mit einheitlicher Koordinatenbezifferung
ausgegeben werden. Die Kurven müssen meist skaliert werden, um alle Kanäle
gut sichtbar zu erhalten. Wenn das nicht beachtet wird, erscheinen kleine
Größen bei sehr unterschiedlichen Zahlenwerten nicht in der Grafik.
Bild 5.3: Strom und Spannung beim Schaltvorgang
5.2 Wechselstromsteller
Beim Wechselstromsteller wird die Ausgangsspannung uL stetig durch die Anschnittsteuerung
über α verstellt. Im Stromnulldurchgang sperren die Ventile bei
τδ. Wechselstromsteller werden z.B. im Haushalt als Dimmer und in der Industrie
zum Steuern von Werkzeugmaschinen verwendet. Durch Variation der Eingabedaten,
wie des Steuerwinkels α, des Widerstandes R und des Speichers L, können
verschiedene Betriebszustände simuliert werden. Um eine wirksame Steuerung zu
erreichen, muss der Steuerwinkel α immer größer als der aus R und L berechnete
Phasenwinkel ϕ sein. Wird diese Bedingung nicht eingehalten, arbeitet der Wechselrichter
in Vollsteuerung, d.h., am Ausgang liegt die volle Wechselspannung an.

5.2 Wechselstromsteller 71
α τd
x
Bild 5.4: Strom und Spannung bei ohmsch-induktiver Last
Damit bei großer induktiver Belastung die Steuerfähigkeit beider Halbleiter im
Bereich α < ϕ gewährleistet ist, dürfen die Thyristoren bei dieser Last nicht durch
Kurzimpulse gesteuert werden. Da ein Ventil durch den induktiven Strom lange
nach Beenden des Impulses leitend ist, kann mit einem kurzzeitigen Impuls das
antiparallele Ventil nicht gezündet werden, da durch den Kurzschluss des paralle -
len leitenden Thyristors die Ventilspannung Null bleibt. Wenn nach dem Stromnulldurchgang
das zweite Ventil zünden könnte, ist der Zündsignal als Kurzzeitimpuls
schon erloschen. Um dieses Problem zu lösen, muss der Thyristor durch
einen Dauerimpuls gesteuert werden. Er liegt bis zum Nulldurchgang der Spannung
an.
Leider wird durch einen Dauerimpuls die Zündverlustleistung beträchtlich erhöht.
Deswegen ersetzt man den kontinuierlichen Impuls durch viele separate Einzelimpulse,
was die Verlustleistung etwas senkt. Das Beispiel in Bild 5.5 zeigt diesen
Sachverhalt. Dort sind bei einem starken induktivem Anteil (ϕ = 72°) und der
Steuerung mit α = 45° die Impulsfolgen gezeigt. Sie setzen um α versetzt ein und
enden bei dem Zeitwinkel von 180°. Dort führt das Ventil weiterhin Strom, so
dass das antiparallele Ventil erst zünden kann, wenn der Strom Null geworden ist.
Das zweite Ventil wird nach Einsetzen der Impulskette le itend, statt bei 45° schaltet
das Ventil erst bei ca. 80° durch.
Übersteigt der Steuerwinkel den Lastwinkel nach Bild 5.7 ist bei gleicher Belastung
α = 90°. Der sinusförmige Lastspannung bekommt Lücken. Damit wird ihr
Effektivwert kleiner.

72
Tabelle 5.1: Charakteristische Größe
Z = R
L = 0
Z = ωL
R = 0
U
U
U
U
Lá
L
Lá
L
=
Bild 5.5: Zündimpulse bei α = 45° und ϕ = 72°
gültig für den Steuerbereich 0 ≤ α ≤ π
α 1
1−
+ sin 2α
ð 2ð
I
I
Lá
L
=
α 1
1−
+ sin 2α
ð 2ð
gültig für den Steuerbereich π/2 ≤ α ≤ π
⎛ α 1 ⎞
= 2⎜1−
+ sin2α
⎟
⎝ ð 2ð
⎠
5 Wechselwegschaltung
ILá
⎛ α⎞
⎛ 2 1⎞
6
= 4⎜1−
⎟ ⎜cos
α+
⎟+
sin αcos
α
IL
⎝ ð⎠
⎝ 2⎠
ð
Die Ergebnisse der Gleichungen aus Tabelle 5.1 wurden in Bild 5.6 als Steuerkennlinie
aufgetragen. Eine Steuerkennlinie stellt mindestens eine Ausgangsgröße
als Funktion der steuernden Größe dar. Die Steuerkennlinien sind nichtlinear. Die
Spannungs- und Stromkennlinien decken sich bei reiner Wirklast, da ihre Kur venform
bei Z = R und L = 0 gleich sind. Die Kennlinien für gemischt ohmsch-induktive
Last liegen zwischen der Grenzkennlinie für L = 0, falls nur der ohmsche
Widerstand angeschlossen ist, und der Grenzkennlinie für R = 0, falls nur die Induktivität
angeschlossen ist.

5.3 Kennwerte verzerrter Wechselgrößen 73
ULα ILα
UL
IL
ULα
UL
L = 0
R = 0
α in Grad
Bild 5.6: Steuerkennlinien des Wechselstromstellers
Bild 5.7: Strom und Spannung bei α = 90° und hohem induktivem Anteil von α = 72°
5.3 Kennwerte verzerrter Wechselgrößen
ILα
IL
Durch die Schaltvorgänge weichen sowohl die Ströme als auch die Spannungen
von der idealen Sinusform ab. Bei der Leistungsberechnung aus den Momentanwerten
p = u i wird meistens die Spannung vereinfachend rein sinusförmig vorausgesetzt.
Da die folgenden Gleichungen allgemein gelten, wird y als Momentanwert
und Yd als Mittelwert verwendet. Mit Y wird allgemein der Effektivwert bezeichnet.
ILα
IL
ULα
UL

74
( x)
= Y + Yˆ
sin(
x + ϕ ) + Yˆ
sin(
2x
+ ϕ ) + Yˆ
sin(
3x
+ ϕ ) + ...
d
1
1
2
2
3
5 Wechselwegschaltung
y (5.2)
Durch Gleichung (5.2) wird eine verzerrte periodische Wechselgröße beschrieben.
Sie kann mit der Fourier-Analyse in ihre sinusförmigen Komponenten zerlegt
werden. Die verzerrte Originalfunktion y ist aus den sinusförmigen Komponenten
durch Addition nach Betrag und Phase zusammengesetzt.
Der arithmetische Mittelwert Yd, wie er sich als Gleichanteil der Fourier-Analyse
ergibt, berechnet sich nach:
2ð
1
Y d = ∫ y(
x)
dx
(5.3)
2ð
0
Der Effektivwert oder quadratische Mittelwert Y ist:
2ð
1 2
Y = y(
x)
dx
2ð
∫
(5.4)
0
Er errechnet sich auch aus den Komponenten der Fourier-Analyse:
) ) )
2 2 2
2 Y1
Y2
Y3
Y = Yd
+ + + + ...
2 2 2
3
(5.5)
Die Qualität einer Wechselgröße wird durch ihren Grundschwingungsgehalt g
oder den Oberschwingungsgehalt k bestimmt:
Effektivwert
der Grundschwingung
Y
g =
=
(5.6)
Effektivwert
der Gesamtschwingung
2
Y
∑ ∞
1
υ = 1
ν
∞ 2
∑υ= 2
∞
∑υ
= 1
ν
Effektivwert
der Oberschwingungen
Yν
k =
=
(5.7)
Effektivwert
der Gesamtschwingung
2
Y
Die Kurvenform einer periodischen Funktion wird durch die Kenngrößen des
Scheitelfaktors kS oder des Formfaktors kF beschrieben:
Scheitelwert
k S =
für ideale Sinusform ist S 2
Effektivwert
= k
Effektivwert
k F =
für ideale Sinusform ist F 1,
11
arithmetischerMittelwert
= k

5.4 Leistung verzerrter Wechselströme 75
Gleichgrößen Yd sind oft durch Wechselanteile überlagert. Ihr Anteil wird durch
die Welligkeit w angegeben.
w =
∑
1
∞
õ=
Y
d
Y
2
õ
=
2
⎛ Y ⎞
⎜ ⎟
⎜ ⎟
−1
⎝ Yd
⎠
(5.8)
Weitere Kennwerte, die zusätzlich im Auswerteprogramm DAY des SIMPLORERS
ermittelt werden, können sind:
Wechselanteil des Effektivwertes:
Schwingungsgehalt: s −
2
Riffelfaktor:
Crestfaktor:
eff
2
eff
2
d
Y = Y − Y
(5.9)
r
1
= 1 (5.10)
w
Y
− Y
max min
= (5.11)
Yd
( Y Y )
5.4 Leistung verzerrter Wechselströme
5.4.1 Momentanwerte
Max max , min
c = (5.12)
Y
Der Laststrom einer Wechselwegschaltung mit rein ohmscher Last (Bild 5.8) wird
durch die Fourier-Analyse in seine Komponenten zerlegt. Die Spannung uS soll
ideal sinusförmig sein. In diesem Fall sind nur Oberschwingungen der Ordnung
ν = n ± 1 für n = 2,3... vorhanden. Fourier-Analysen lassen sich leicht mit MATH-
CAD durchführen. In der Beispieldatei 1fourier.mcd ist die Zerlegung einer Funktion
durch die Fourier-Analyse mit MATHCAD gezeigt.
Bild 5.8: W1 mit ohmscher Last

76
i
ϕ1
α
x
Bild 5.9: Ergebnis der Fourier-Analyse des Laststroms
5 Wechselwegschaltung
Beispielhaft ist die Fourier-Analyse mit der MATHCAD-Datei w1.mcd durchgeführt.
Bild 5.9 zeigt den angeschnittenen Strom mit den Fourier-Komponenten.
Die Phasenverschiebung ϕ1 der Grundschwingung des Stromes und der Spannung
ist zur der Berechnung der Wirkleistung wichtig. Wegen der sinusförmig angenommenen
Netzspannung trägt nur die Grundschwingung des Stromes zur Wirkleistung
bei. Die Oberschwingungen bilden die Blindle istungskomponenten. Von
den existierenden ungeradzahligen Oberschwingungen sind nur diejenigen für
ν = 3; 5 und 7 gezeichnet. Der Effektivwert der Grundschwingung ist der Bezugswert.
Oberschwingungsspektrum für α = 60°
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Bild 5.10: Amplitudenspektrum des Laststromes
ν

5.4 Leistung verzerrter Wechselströme 77
Mit MATHCAD kann sowohl die Fourier-Analyse als auch deren Rekonstruktion
durchgeführt werden. Sie ist in der Datei w1.mcd durch den Ausdruck
∑
( Re( C ) cos( υ x)
+ Im( C ) sin( υx)
)
i x)
: = C +
(5.13)
rec ( 0
υ
υ
formuliert. Bei der Rekonstruktion wurden die Fourier-Koeffizienten bis zur 19.
Oberschwingung addiert. Dabei ist zu beachten, dass die Angabe des Amplitudenspektrums
allein zu einer Rekonstruktion nicht ausreicht. Es müssen zusätzlich die
Phasenverschiebungen der Oberschwingungen zur Bezugsfunktion berücksichtigt
werden.
0
Bild 5.11: Rekonstruktion des verzerrten Stromes
Die Wirkleistung P ist der arithmetischer Mittelwert des Produktes aus Strom und
Spannung p = u⋅ i.
2ð
1
P = ∫u(
x)
i(
x)
dx
(5.14)
2ð
0
Sind sowohl der Strom als auch die Spannung verzerrt, ergibt sich die Wirkleistung
aus dem Produkt der Oberschwingungen gleicher Ordnung ν. Dieser Sachverhalt
muss gegenwärtig mehr Beachtung finden, da von einer idealen sinus förmigen
Versorgungsspannung heutzutage nicht mehr ausgegangen werden kann.
Die Spannung wird zunehmend durch nichtlineare Verbraucher verzerrt. Es können
daher gleiche Oberschwingungsanteile sowohl in der Spannung als auch im
Strom vorhanden sein.
∑ ∑
∞
∞
Pí
=
ν = 1 ν = 1
P =
U I cos( ϕ )
(5.15)
í
í
í
υ
i(x) Rekonstruktion aus
Oberschwingungen bis zur 19.
x

78
5 Wechselwegschaltung
Im Falle sinusförmiger Netzspannung kann nur die Grundschwingung des Stromes
i1 zur Wirkle istungsbildung beitragen. Aus Gleichung (5.15) folgt:
P = P = UI ϕ )
(5.16)
1
1 cos( 1
Die Momentanwerte der Grundschwingungsleistung haben doppelte Netzfrequenz.
In Gleichung (5.17) ist der erste Summand eine pulsierende Gleichgröße, deren
Momentanwerte immer größer als Null sind. Der arithmetische Mittelwert entspricht
der Wirkleistung P. Der zweite Summand ist eine reine Wechselgröße mit
dem arithmetischen Mittelwert Null. Er gibt die Blindleistungsmomentanwerte der
Grundschwingung wieder, deren absoluter Mittelwert der Grundschwingungsblindleistung
Q1 entspricht.
p ( x)
= UI sin( x)
cos( x + ϕ )
1
1
1
1
1
p ( x)
= UI
1
p ( x)
= UI
1
1
[ cos( ϕ1
) − cos( 2x
+ ϕ1)
]
cos( ϕ ) − UI [ cos( 2x)
cos( ϕ ) − sin( 2x)
sin( ϕ ) ]
1
1
1
1
p ( x)
= UI cos( ϕ )( 1−
cos( 2x))
+ UI sin( ϕ ) sin 2x)
p
p
0
0
α = 60°
α = 60°
Bild 5.12: Leistungen der W1-Schaltung
1
1
Aufteilung in Blind- und Wirkleistung
1
Aufteilung in Grundschwingungsleistung p1
und Verzerrungsleistung pv
1
x
x
(5.17)

5.4 Leistung verzerrter Wechselströme 79
Die Aufteilung der Leistung p in reine Wirkleistung pW und reine Blindleistung pB
erfolgt in Bild 5.12. Subtrahiert man von der Leistung p, die nur aus der Grundschwingung
des Stromes gebildete Momentanwert der Grundschwingungsleistung
p1, bleibt eine Restleistung pv übrig. Sie ergibt sich aus der Verzerrung des Laststroms.
Da der Mittelwert der Funktion pv = 0 ist, handelt es sich um eine reine
Blindleistung, die Verzerrungsblindleistung heißt.
5.4.2 Leistungsmittelwerte
Berechnet man die Leistungen aus den Effektivwerten der Spannungen und Ströme,
ergeben sich folgende Zusammenhänge:
2 2 2
• Scheinleistung: S = UI = U I + I + I + ... (5.18)
Die Scheinleistung ist S = U I. Da der Effektivwert I aus einer verzerrten Größe
gebildet wird, ergibt sich S aus einer Summe gemäß Gleichung (5.18).
• Grundschwingungsscheinleistung:
• Grundschwingungsblindleistung:
1
2
3
2 2
1 = UI 1 = P Q1
(5.19)
S +
2 2
1 = UI 1 sin( ϕ 1)
= S1
P
(5.20)
Q −
• Wirkleistung ( ) UI P = (5.21)
• Gesamtblindleistung
1 1 cosϕ
Q −
2 2
= S P
(5.22)
2 2 2 2
• Verzerrungsleistung: D = Q − Q = U I + I + ... (5.23)
Weil die Zeiger von P und Q1; sowie Q und D senkrecht aufeinander stehen, ergeben
sich die Gleichungen (5.20), (5.21), (5.22) und (5.23). Die Leistungen lassen
sich als Kanten eines Tetraeders in Bild 5.13 zeichnen.
Im Falle eines unverzerrten Stroms wird die Verzerrungsleistung D = 0. S wird zu
S1 und Q deckt sich mit Q1. Wegen der sinusförmig angenommenen Eingangsspannung
gilt immer P = P1. Es ergibt sich dann das aus den Grundlagen der Elektrotechnik
bekannte Zeigerbild der Leistungen.
1
2
3

80
Bild 5.13: Geometrische Darstellung der Leistungen
5.4.3 Der Leistungs- und Verschiebungsfaktor
5 Wechselwegschaltung
Der Leistungsfaktor ist durch Gleichung (5.24) definiert. Er stimmt nur bei sinusförmigen
Wechselgrößen mit dem cos(ϕ) überein. In diesem Sonderfall ist
cos(ϕ) = cos(ϕ1).
P Wirkleistung
λ = =
(5.24)
S Scheinleistung
Allgemein berechnet sich der Leistungsfaktor aus dem Grundschwingungsgehalt
und der Phasenverschiebung der Grundschwingung mit dem Verschiebungsfaktor
cos(ϕ1).
λ i g =
cos( ϕ1
)
(5.25)
Wenn verzerrte Ströme und Spannungen vorliegen, muss der Leistungsbegriff erweitert
werden. Nur die Wirkleistung ist eindeutig bestimmt. Bei der Blindleistung
gibt es unterschiedliche Definitionen. Obwohl wir es mit einem reinen ohmschen
Verbraucher zu tun haben, wird von der Schaltung Blindleistung aufgenommen,
sobald sie angesteuert wird. Man spricht von Steuerblindleistung Q1 und Verzerrungsblindleistung
D. In Mehrphasensystemen kann zusätzlich durch Unsymmetrien
Blindleistung entstehen, die Unsymmetrie-Blindleistung.
5.4.4 Anwendungsbeispiel
Die einphasige W1-Schaltung wird als Dimmerschaltung zur Reduzierung der
Wirkleistung von Lampen eingesetzt. Allerdings wird der Effekt durch zusätzliche
Erzeugung von Blindleistung erkauft. Man verwendet für die Schaltung Triacs. Sie
werden durch Potentiometer gesteuert.

5.4 Leistung verzerrter Wechselströme 81
Für die rein ohmsch belastete W1-Schaltung lassen sich der Grundschwingungsgehalt
g sowie der Verschiebungsfaktor cos(ϕ1) und Leistungsfaktor λ nach folgenden
Gleichungen ausrechnen. Die Funktionen sind aus Bild 5.15 ersichtlich.
Grundschwingungsgehalt
2 ( ð −α)
+ ( ð −α)
Bild 5.14: Dimmerschaltung
2
1
sin 2α+
sin α
g i =
(5.26)
ð α 1
1−
+ sin 2α
ð 2ð
Phasenwinkel der Grundschwingung
2
− sin α
ϕ1
= arctan
(5.27)
1
ð −α+
sin 2α
2
Verschiebungsfaktor
Leistungsfaktor
1
ð −α
+ sin 2α
cosϕ
=
2
(5.28)
1
2
2
( ð −α)
+ ( ð −α)
sin 2α+
sin α
α 1
λ = 1 − + sin 2α
(5.29)
ð 2ð

82
gi
cos ϕ1
λ
ϕ1
Bild 5.15: Kenngrößen der W1-Schaltung bei ohmscher Last
λ
5 Wechselwegschaltung
gi
cos ϕ1
α
α