Mathematische Populationsmodelle oder Was bewirkt DDT?

Mathematische Populationsmodelle 

oder 

Was bewirkt DDT? 

Martin Pohl 

Fachhochschule Regensburg 

Fakultät für Informatik und Mathematik 

MNU-Tag Regensburg, 

15. 02. 2007 

Martin Pohl (FH Regensburg, FB IM) Populationsmodelle 15. 02. 2007 1 / 32

Inhaltsübersicht 

1 Mathematische Modelle 

2 Modelle für eine Population 

Differentialgleichungen erster Ordnung 

Exponentielles Wachstum 

Logistisches Wachstum 

3 Modelle für zwei Populationen 

Vorbemerkungen 

Das Räuber-Beute Modell von Volterra 

Untersuchung der Lösungen in der Phasenebene 


Wozu Mathematik? 

Mathematik erklärt die Welt. 

Mathematik ist die Antwort des Menschen auf die 

Komplexität der Welt. 

Die Mathematik ist eine wunderbare Lehrerin für die 

Kunst, die Gedanken zu ordnen, Unsinn zu beseitigen 

und Klarheit zu schaffen. 

(J. H. Fabre) 


Wozu mathematische Modelle? 

Modelle helfen Verstehen und Entscheiden 

Einfache mathematische Modelle statt schwieriger 

„real-world“-Probleme 

Einfache Modelle durch einfache Annahmen 

Verifizierung von nicht kausal begründbaren Modellen — 

Vergleich realer Daten mit Ergebnissen des Modells 

Sensitivitätsanalyse — quantitativ und qualitativ 


Modellkategorien 

Empirische Modelle: Anpassung von Kurven an Messdaten 

Stochastische Modelle: Grundlage sind Wahrscheinlichkeiten für 

das Auftreten von Ereignissen 

Deterministische Modelle: Prozessbeschreibung durch 

Gleichungen wie z.B. Differentialgleichungen 

Simulationsmodelle: Nachbildung des Prozesses mit einem 

Computerprogramm 

Statistische Modelle: Testen von Hypothesen mit Hilfe von 

Stichproben 


Modellierungsprozess 

Prozess wird mehrfach zyklisch durchlaufen 

Ziel: Kompromiss zwischen Genauigkeit und Lösbarkeit 

Die Schritte im einzelnen: 

1 Identifikation und Beschreibung des Problems 

2 Treffen von Annahmen (−→ einfaches Modell) 

3 Erstellen von Gleichungen: 

Flussdiagramme −→ verbale Gleichungen −→ 

Differentialgleichungen 

4 Lösen der Gleichungen: analytisch oder numerisch 

5 Darstellung und Interpretation der Ergebnisse 


Annahmen aller Populationsmodelle 

Annahmen 

1 Die Population ist sehr groß 

Größe der Population ist ganzzahlig 

Annäherung durch eine stetig differenzierbare Funktion möglich 

2 Alles passiert sofort 

Keine Zeitverzögerung, keine „Einschwingphase“ 

Geburts- und Sterberaten unabhängig vom Alter 



Definition 

Die Gleichung 

dy 

dx = y ′ = f (x, y) 

heißt Differentialgleichung (DGL) erster Ordnung. 

y ′ = f (x, y), y(x0) = y0 heißt Anfangswertproblem (AWP). 

y ′ = g(x) · h(y) heißt DGL mit getrennten Variablen. 

Bemerkung 

Ist x von der Zeit t abhängig, so schreibt man 

dx 

dt 

= 

x = f (x, t) 



Satz 

Ist die Funktion f und die partielle Ableitung ∂f 

stetig, so ist das 

∂y 

AWP 

lokal eindeutig lösbar. 

y ′ = f (x, y), y(x0) = y0 

Für die DGL y ′ = g(x) · h(y) mit getrennten Variablen gilt: 

Jede Nullstelle y0 von h ist eine konstante Lösung. 

Ist H ′ (y) = 1 

h(y) und G′ (x) = g(x), so kann man die 

Lösungskurven implizit darstellen als Lösungen der Gleichung 

H(y) = G(x) + C, C ∈ R. 



Bemerkung 

Formale Lösung von y ′ = g(x) · h(y): 

dy 

dx 

dy 

= g(x) · h(y) =⇒ = g(x) dx 

h(y) 

Integration beider Seiten ergibt: 

 

dy 

h(y) = 

 

g(x) dx ⇐⇒ H(y) = G(x) + C, C ∈ R 


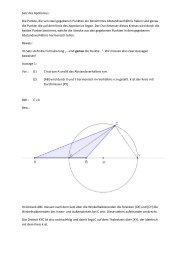
Geometrische Deutung 

Steigung der Lösung im Punkt 

(x0, y0) ist f (x0, y0) 

Pfeil durch (x0, y0) mit dieser 

Steigung ist tangential zu der 

Kurve 

Lösungskurven schmiegen sich 

in das Richtungsfeld 


Exponentielles Wachstum, Modell 

Annahmen 

Größe P der Population stetig differenzierbar 

Individuelle Geburtenrate pro Zeiteinheit ist β 

(konstant und von P unabhängig) 

Individuelle Sterberate pro Zeiteinheit ist α 

(konstant und von P unabhängig) 

Keine externen Einflüsse 

(Einwanderung, Auswanderung, Fang, Ernte) 



Beispiel 

Daten für die Erdbevölkerung (Stand 1990) sind: 

Geburtenrate pro Kopf ist β = 0.027 pro Jahr 

Sterberate pro Kopf ist α = 0.010 pro Jahr 

Daten für die Bevölkerung von Australien: 

β = 0.014 und α = 0.007 



Modell 

Zunahme von P durch Geburten: βP 

Abnahme von P durch Tode: αP 

Änderungsrate von P: 

dP 

= P = βP − αP 

dt 

Effektive individuelle Änderungsrate: λ = β − α 

Anfangswert P(0) = P0 

Resultierendes AWP: 

 

P = λP, P(0) = P0 


Exponentielles Wachstum, Lösung 

=⇒ 

P>0 

dP 

dt 

Gegebenes AWP: 

= λP =⇒ dP 

P 

 

P = λP, P(0) = P0 

= λ dt =⇒ 

 

dP 

P = 

 

λ dt 

ln P = λt + ˜ C =⇒ P = e λt+ ˜ C =⇒ P(t) = C e λt 

Mit C = P(0) = P0 erhält man schließlich 

P(t) = P0 e λt 


Diskussion der Lösung 

Weltbevölkerung, 

t = 0 für 1990 

λ = 0.017 und 

P0 = 5.3 · 10 9 

Modell für lange Zeiträume ungenügend 

P(t) = 5.3 · 10 9 · e 0.017t 

Verlauf vom U.S. Census 

Bureau 

Modell ←→ Wirklichkeit 


Verbesserungen des Modells 

Werte für Vergangenheit 

zu klein, 

Wachstumsrate nicht 

konstant 

Qualitativer Kurvenverlauf 

für Zukunft nicht zutreffend 

Effektive Wachstumsrate 

sinkt bei großer 

Bevölkerung 

Große Population −→ Konkurrenz um begrenzte Ressourcen 

−→ Sterberate steigt 

Hohe Populationsdichte −→ ev. sinkende Geburtenrate 


Logistisches Wachstum, Modell 

Annahmen 

P ist stetig differenzierbar 

P(t) ≤ K , K ist die maximale Kapazität 

Individuelle Geburtenrate ist β 

Individuelle Sterberate wächst linear mit P sie ist α + γP 

Keine externen Einflüsse 


Logistisches Wachstum, Modell 

Modell 

Zunahme von P durch Geburten: βP 

 

Abnahme von P durch Tode: α + γP · P = αP + γP 2 

Änderungsrate von P: 

λ = β − α 

Anfangswert: P(0) = P0 

Resultierendes AWP: 

 

P = βP − αP − γP 2 

 

P = λP − γP 2 , P(0) = P0 


Logistisches Wachstum, qualtitative Diskussion 

 

P = λP − γP 2 = P λ − γP = 0 =⇒ P = 0 oder P = λ 

γ 

0 

γ 

P > λ 

γ 

=⇒ 

P > 0 

=⇒ 

P < 0 

P0 > 0 =⇒ lim P(t) = 

t→∞ λ 

γ 

Kapazität ist K = λ 

γ 

γ = λ 

 

=⇒ P = λP 

K 1 − P 

K 



Krümmungsverhalten und Wendepunkte im Fall 0 

 

 

P = λP 1 − P 

 

=⇒ 

K 

 

P = λ 

 

P 1 − P 

 

P 

− λP = λP 1 − 

K K 2P 

 

K 

P < K 

2 

P > K 

2 

=⇒ 

P > 0 

=⇒ 

P < 0 

Wendepunkt bei P = K 

2 

lim P(t) = K 

t→∞ 

S-förmiger Kurvenverlauf 



Bemerkung 

Eine Anwendung ist die Marktforschung: 

Die Kapazität (hier Marktdurchdringung) kann man abschätzen, wenn 

man in den Absatzzahlen einen Wendepunkt feststellt. 


Logistisches Wachstum, Lösung 

Gegebenes AWP: 

dP 

dt = λP K − P 

K 

=⇒ 

0

Logistisches Wachstum, Lösung 


Logistisches Wachstum, Erweiterungen 

Einfluss einer konstanten Ernterate h: 

 

 

P = λP 1 − P 

 

− h= − 

K 

λ 

 

P 

K 

2 − KP + Kh 

 

λ 

stationäre Lösungen sind: P1, 2 = K 

 

1 ± 1 − 

2 

4h 

 

K λ 

1 h ≥ 

2 h < 

K λ 

4 =⇒ 

K λ 

4 

P ≤ 0 =⇒ Population stirbt aus 

P2 

t→∞ P(t) = P1 = K 

2 

 

1 + 

P < P2 =⇒ 

P < 0 =⇒ Population stirbt aus 

 

1 − 4h 

 

K λ 





Einfluss einer konstanten Fangquote h0: 

 

 

P = λP 1 − P 

 

− h0P= − 

K 

λ 

K P 

 

P − K 1 − h0 

 

λ 

 

 

stationäre Lösungen sind P = 0 und P = K 1 − h0 

 

λ 

 

1 h0 < λ =⇒ lim P(t) = K 1 − 

t→∞ h0 

 

λ 

2 h0 ≥ λ =⇒ lim 

t→∞ P(t) = 0 

−→ h0 muss reduziert werden zu einem h0 < λ 




Modellbeispiele mit zwei Populationen 

Wettbewerbsmodelle: Konkurrenz um begrenzte Ressourcen. 

Stabile Lösungen erst mit mindestens drei Populationen. 

Symbiose: Positive Wechselwirkung. 

Epidemien: Infizierte und Anfällige. Ausbruch oberhalb eines 

Schwellenwertes möglich. 

Gefechtsmodell: Schlachten zwischen zwei Armeen. Ergebnisse 

waren den Feldherren des 18. Jhd. bekannt. 

Räuer-Beute Modelle: Beutepopulation hat unbegrenzten 

Nahrungsvorrat, Räuber ernähren sich nur von der Beute. 


Systeme von Differentialgleichungen erster Ordung 

Definition 

Das System 

 

x = f (x, y) 

 

y = g(x, y) 

heißt autonomes System von Differentialgleichungen erster 

Ordnung. 

Die Lösungen (x0, y0) des Gleichungssystems 

f (x, y) = 0 

g(x, y) = 0 

heißen stationäre Lösungen oder Gleichgewichtslagen. 



Bemerkung 

Die Gleichgewichtslagen (x0, y0) sind gerade die konstanten 

Lösungen von 

 

x = f (x, y) 

 

y = g(x, y) 



Satz 

Sind die Funktionen f (x, y) und g(x, y) und deren partielle 

Ableitungen nach x und y stetig, so ist das AWP 

lokal eindeutig lösbar. 

 

x = f (x, y), x(0) = x0 

 

y = g(x, y), y(0) = y0 


Die Phasenebene 

Geometrische „Theorie“ der Lösungen von 

 

x = f (x, y) 

 

y = g(x, y) 

Die Lösungen x(t) und y(t) definieren die Trajektorie x(t), y(t) ∈ R 2 

Die Menge aller Trajektorien heißt Phasenportrait. 

In (x0, y0) läuft die Trajektorie in Richtung f (x0, y0), g(x0, y0) T 

Einen geometrischen Eindruck über den Verlauf der Trajektorien 

ermöglicht das Richtungsfeld. 

Bemerkung 

Lösungen eindeutig ⇐⇒ Trajektorien schneiden sich nicht 





Wie findet man die Trajektorien? 

Annahme: Trajektorie ist lokal darstellbar als y = y(x) 

=⇒ dy 

dx 

= dy/dt 

dx/dt = 

 

y 

 

x 

= g(x, y) 

f (x, y) 

Elimination von t führt zu der DGL y ′ = 

g(x, y) 

f (x, y) 

Nachteil: Information über zeitlichen Verlauf geht verloren 

Vorteil: Manche Eigenschaften der Trajektorien leicht zu beweisen 


Räuber-Beute Modell 

Annahmen 

Es gibt nur die zwei Populationen: 

„Beute“-Population B der Größe B(t), unbegrenzte 

Nahrungsvorräte, alle werden gefressen. 

„Räuber“-Population R der Größe R(t), B ist einzige Nahrung. 

Beispiele 

B sind Speisefische, R sind Raubfische, z.B. Haie. 

B sind Schädlingsinsekten, R sind deren natürliche Feinde (z.B. 

andere Insekten). 


Volterrasches Räuber-Beute Modell, Geschichte 

Vor 80 Jahren untersucht der italienische Biologe D’Ancona die Wechselwirkungen 

verschiedener Fischarten: 

Fischfang reduziert =⇒ 

Anteil Haie größer 

Anteil Speisefische kleiner 

Räuber profitieren mehr vom Rückgang der Fischerei als 

Speisefische. 

D’Ancora fand hierfür keine biologische Erklärung. 

Er bittet den Mathematikkollegen Volterra um Hilfe. 

Volterra entwickelt das Räuber-Beute Modell und beantwortet die 

Frage von D’Ancora. 



Annahmen 

B und R sind stetig differenzierbar 

Individuelle Geburtenrate der Beute ist β1 

Individuelle Sterberate der Beute ist proportional zu R 

Individuelle Geburtenrate der Räuber ist proportional zum 

Nahrungsangebot 

Individuelle Sterberate der Räuber ist α2 

Keine externen Einflüsse (Fischfang, DDT) 



Modell 

Geburtenrate der Beute: β1B 

Sterberate der Beute: c1RB 

 

Änderungsrate Beute: B = β1B − c1RB 

Geburtenrate der Räuber: f · c1RB = c2RB 

Sterberate der Räuber: α2R 

 

Änderungsrate Räuber: R = c2BR − α2R 

Resultierendes DGL-System: 

 

B = β1B − c1BR = B β1 − c1R 

 

R = c2BR − α2R = R 

c2B − α2 


Räuber-Beute Modell, Interpretation 

Beute allein: exponentielles Wachstum mit Rate β1 

Räuber allein: exponentielles Aussterben mit Rate α2 


Räuber-Beute Modell, Interpretation 

Wechselwirkung zwischen B und R: 

Betrachtung eines kurzen Zeitintervalls ∆t: 

Jeder Räuber sucht pro Zeiteinheit den Anteil a der Fläche ab. 

Jeder Räuber hat ein eigenes Jagdrevier. 

Zeit zum Verzehr der Beute wird vernachlässigt. 

Während ∆t fängt jeder Räuber aB∆t Beutetiere. 

Gesamte Sterberate von B ist aBR = c1BR. 

c1 ist die Suchrate der Räuber. 

(pro Zeiteinheit bejagter Flächenanteil) 

Sterberate Beute = c1BR = Nahrungsangebot 

Geburtenrate Räuber = f · c1BR = c2BR 

f = c2 = Anzahl der Beutetiere, die für eine Geburt eines Räubers 

c1 

gefressen werden. 

f ist ein Maß für den Nahrungsbedarf der Räuber. 


Räuber-Beute Modell, Lösung 

Das Räuber-Beute Modell kann nicht explizit gelöst werden. Die 

numerisch ermittelten Lösungen sehen folgendermaßen aus: 

B(t) und R(t) sehen periodisch aus. 

R(t) hinkt gegenüber B(t) um eine viertel Periode hinterher. 


Räuber-Beute Modell, Varianten 

Externe Engriffe: Fangquoten 

Fangquoten wirken sowohl auf B als auch auf R 

Sterberate von B um p1B erhöht 

Sterberate von R um p2R erhöht 

Modifiziertes Modell ist: 

 

B = β1B − c1BR − p1B 

 

R = c2BR − α2R − p2R 





Kapazität K für Beutepopulation 

Mit R = 0 logistisches Wachstum für B 

Modifiziertes Modell ist: 

 

B = β1B 

 

R = c2BR − α2R 

 

1 − B 

 

− c1BR 

K 

Jetzt streben die Lösungen einem Grenzwert zu 





Beobachtung verschiedener realer Systeme zeigt: 

Volterra-Modell beschreibt manche Systeme gut. 

Erweiterung mit logistischem Wachstum beschreibt manche 

Systeme gut. 

Für manche Systeme passen die Modelle nicht: 

Ohne Räuber logistisches Wachstum. 

Mit Räuber periodisches Verhalten. 

Erweiterung von Holling-Tanner: 

Fresszeiten werden berücksichtigt. 

Räuber fressen nichts, wenn sie satt sind. 

Kapazität für Räuber, abhängig von Beutepopulation. 

Ergebnis: Logistisches Wachstum und periodische Grenzwerte. 


Übergang zur Phasenebene 



Erste Diskussion der Trajektorien von 

 

B = β1B − c1BR = B β1 − c1R 

 

R = c2BR − α2R = R 

c2B − α2 

Stationäre Punkte: (0, 0) und (B0, R0) = 

 

 

 

α2 

, 

c2 

β1 

c1 

B > 0 ⇐⇒ R < R0 und B < 0 ⇐⇒ R > R0 

 

 

R > 0 ⇐⇒ B > B0 und R < 0 ⇐⇒ R < R0 

Links von B = B0 nach unten, rechts von B = B0 nach oben 

Über R = R0 nach links, unter R = R0 nach rechts 

Trajektorien laufen im Uhrzeigersinn um den Punkt (B0, R0). 



Mögliche Trajektorienverläufe in der Phasenebene 


Gleichungsdarstellung der Trajektorien 

Anwendung der Kettenregel auf das System 

ergibt 

dR 

dB = 

 

B = β1B − c1BR = B β1 − c1R 

 

R = c2BR − α2R = R 

c2B − α2 

 

R 

 

B 

= R(c2B − α2) 

B(β1 − c1R) = 

also eine DGL mit getrennten Variablen. 

R 

β1 − c1R · c2B − α2 

B 



dR 

dB = 

R 

β1 − c1R · c2B − α2 

=⇒ 

B 

β1 

R 

− c1 

=⇒ β1 − c1R 

dR = 

R 

c2B − α2 

B 

 

dR = c2 − α2 

 

dB 

B 

=⇒ β1 ln R − c1R = c2B − α2 ln B + ˜ C 

=⇒ β1 ln R − c1R + α2 ln B − c2B = ˜ C 

Anwendung der e-Funktion ergibt 

R β 1 · B α 2 

e c 1R · e c 2B = Bα 2 

e c 2B · Rβ 1 

e c 1R 

= C, C > 0 

Martin Pohl (FH Regensburg, FB IM) Populationsmodelle 15. 02. 2007 28 / 32 

dB


Mit den Funktionen 

f (B) = Bα 2 

e c 2B 

und g(R) = Rβ 1 

e c 1R 

sind die Trajektorien die Lösungsmengen der Gleichung 

f (B) · g(R) = C, C > 0 


Periodizität der Lösungen 

Trajektorien geschlossene Kurven =⇒ Lösungen periodisch 

x a 

Zunächst: Kurvendiskussion von h(x) = , 

ebx a, b > 0, x ≥ 0 

h(0) = 0, lim h(x) = 0 

x→∞ 

x > 0 =⇒ h(x) > 0 

=⇒ globales Maximum von h bei Nullstelle der Ableitung 

h ′ (x) = ax a−1 − bx a 

e bx 

= x a−1 

e bx 

 

>0 für x>0 

· a − bx 

Das Maximum von h wird an der Stelle x0 = a 

b angenommen. 



Folgerungen für die Funktionen f und g: 

f (B) = Bα 2 

e c 2B nimmt ihr Maximum an der Stelle B = B0 = α2 

Der Maximalwert von f ist M f = f (B0). 

g(R) = Rβ 1 

e c 1R nimmt ihr Maximum an der Stelle R = R0 = β1 

Der Maximalwert von g ist Mg = g(R0). 


c2 

c1 

an. 

an.


Wann sind die Lösungskurven von f (B) · g(R) = C geschlossen? 

1 Für vorgegebenes C1 > 0 gibt es keine Lösung. 

2 Für vorgegebenes C2 > 0 gibt es genau eine Lösung, nämlich 

(B0, R0). 

3 Für vorgegebenes C3 > 0 ist die Lösungsmenge eine 

geschlossene Kurve: 

Es gibt zwei Werte B1 < B0 und B2 > B0 mit: 

B < B1 oder B > B2 =⇒ f (B) · g(R) = C3 hat keine Lösung R 

Für B = B1 oder B = B2 hat f (B) · g(R) = C3 nur die Lösung 

R = R0 

Für B ∈ (B1, B2) hat f (B) · g(R) = C3 genau zwei Lösungen 

R1(B) < R0 und R2(B) > R0 

Es ist lim 

B→B1+ R1, 2(B) = R0 und lim 

B→B2− R1, 2(B) = R0 



f (B) · g(R) = C, C > 0, 

f (B) ≤ f (B0) = M f , g(R) ≤ g(R0) = Mg 

1 C1 > M f · Mg =⇒ es gibt keine Lösung 

2 C2 = M f · Mg =⇒ es gibt nur die Lösung (B0, R0) 

3 0 < C3 < M f · Mg =⇒ f (B) · g(R) = µ · Mg, 0 < µ < M f 

⇐⇒ g(R) = µ 

f (B) · Mg ist zu lösen 



3 g(R) = µ 

f (B) · Mg, 0 < µ < Mf f (B) = µ =⇒ B = B1 < B0 oder B = B2 > B0 

B < B1 oder B > B2 =⇒ f (B) < µ =⇒ µ 

> 1 

B1 µ =⇒ µ 

< 1 

f (B) 

f (B) 

B < B1 oder B > B2 =⇒ µ 

µ 

> 1 =⇒ g(R) = · Mg 

f (B) f (B) 

B = B1, 2 =⇒ µ 

 

= 1 =⇒ g(R) = 

f (B) µ 

f (B) · Mg 

 

⇐⇒ R = R0 

B1 

µ 

< 1 =⇒ g(R) = 

f (B) f (B) · Mg hat zwei 

Lösungen R1 < R0 und R2 > R0 

B → B1+ =⇒ R1, 2 → R0 und B → B2− =⇒ R1, 2 → R0 


Mittelwerte der Populationen 

Trajektorien geschlossen =⇒ Lösungen periodisch, d.h. es gibt 

ein T mit B(t + T ) = B(t) und R(t + T ) = R(t) für alle t. 

Die (Zeit-)Mittelwerte B von B(t) und R von R(t) sind 

Es gilt 

T 

0 

B = 1 

T 

T 

0 

 

B(t) 

B(t) dt= lnB(t) T 

 

B(t) dt und R = 1 

T 

Aus der DGL 

B = B(β1 − c1R) folgt: 

0 = 1 

T 

T 

0 

 

B 1 

dt= 

B T 

T 

0 

0 

T 

0 

R(t) dt 

= ln B(T ) − ln B(0) = 0 

T 

 

β1 − c1R dt= β1 − c1 · 1 

R dt 

T 0 

 


=R

Mittelwerte der Populationen 

Der Mittelwert von R ist daher 

Analog erhält man: 

Bemerkung 

R = β1 

c1 

B = α2 

c2 

= R0 

= B0 

Die Lösungen des Volterraschen Räuber-Beute Modells sind 

periodisch. Die stationäre Lösung stimmt mit den Mittelwerten der 

Populationen überein, (B, R) = (B0, R0). 


Zurück zu D’Ancona 

Räuber-Beute Modell für Haie und Speisefische mit konstanter 

Fangquote: 

 

B = β1B − c1BR − p1B = B (β1 − p1) − c1R 

 

R = c2BR − α2R − p2R = R c2B − (α2 + p2) 

p1 > 0: Fangquote der Speisefische, p2 > 0: Fangquote der Haie 

Mittelwerte der Populationen mit Fischfang: 

B1 = α2 + p2 

c2 

und R1 = β1 − p1 

c1 

Fischfang =⇒ mehr Speisefische aber weniger Haie. 


Zurück zu D’Ancona 


Was hat das mit DDT zu tun? 

1868: „Einfuhr“ des Baumwollschuppen-Insekts von Australien 

nach Amerika 

Folge: Zitrusfrüchteindustrie stark bedroht 

Maßnahme: Einfuhr der natürlichen Feinde, einer Marienkäferart 

Folge: Erträgliche Reduzierung der Schädlinge 

Maßnahmen nach Erfindung von DDT: 

Einsatz des Mittels zur weiteren Reduzierung der Schädlinge 

Folgerung aus dem Räuber-Beute Modell: 

Schädlinge nehmen zu, Fressfeinde nehmen ab 

Kann so ein mathematisches Modell stimmen? „Nein“ ??? 

Und die Folgen? 


Was hat das mit DDT zu tun? 

Es gibt Dinge, die den meisten Menschen unglaublich erscheinen, die 

nicht Mathematik studiert haben. 

(Archimedes)

Mathematische Populationsmodelle oder Was bewirkt DDT?

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?