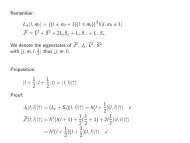Grundlagen der Quantenmechanik und Statistik - Institut für ...
Grundlagen der Quantenmechanik und Statistik - Institut für ...
Grundlagen der Quantenmechanik und Statistik - Institut für ...
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
<strong>Gr<strong>und</strong>lagen</strong> <strong>der</strong><br />
<strong>Quantenmechanik</strong> <strong>und</strong> <strong>Statistik</strong><br />
Teil I: <strong>Quantenmechanik</strong><br />
Vorlesungen an <strong>der</strong> Ruhruniversität Bochum<br />
K.–U. Riemann
1. Einführung<br />
Inhaltsverzeichnis<br />
1.1 Historische Ausgangssituation 1<br />
Lord Kelvins dunkle Wolken<br />
1.2 Korpuskeleigenschaft des Lichts 2<br />
1.3 Welleneigenschaften <strong>der</strong> Materie 3<br />
1.4 Welle–Teilchen–Dualismus <strong>und</strong> Komplementarität 4<br />
Positivismus <strong>und</strong> Realismus<br />
1.5 Gr<strong>und</strong>begriffe <strong>der</strong> Wellenbeschreibung 6<br />
Dispersionsgleichung<br />
Phasen– <strong>und</strong> Gruppengeschwindigkeit<br />
Unschärfeprodukt<br />
1.6 Gr<strong>und</strong>begriffe <strong>der</strong> Wahrscheinlichkeitsrechnung 9<br />
Kolmogorovsches Axiomensystem<br />
Diskrete <strong>und</strong> kontinuierliche Zufallsvariablen<br />
Mittelwerte, Momente, Varianz<br />
2. Die Schrödingergleichung<br />
2.1 Entwicklung <strong>der</strong> Wellengleichung 12<br />
Das Korrespondenzprinzip<br />
2.2 Formale Eigenschaften <strong>der</strong> Schrödingergleichung 14<br />
2.3 Die Kontinuitätsgleichung 15<br />
Die Teilchen–Stromdichte<br />
2.4 Erwartungswerte <strong>und</strong> Operatoren 18<br />
Der Impulsoperator<br />
Der Hamiltonoperator<br />
Der Drehimpulsoperator<br />
Hermitesche Operatoren<br />
Hilbertraum <strong>und</strong> Dualraum, bra– <strong>und</strong> ket–Vektoren<br />
2.5 Das Theorem von Ehrenfest 22<br />
i
2.6 Die Heisenbergsche Unschärferelation 25<br />
Die Orts–Impuls–Unschärfe<br />
Die allgemeine Unschärferelation<br />
Die Drehimpuls–Unschärfe<br />
Heisenbergs Gedankenexperiment<br />
Die Energie–Zeit–Unschärfe<br />
3. Spezielle Lösungen <strong>der</strong> Schrödingergleichung<br />
3.1 Entwicklung nach Eigenfunktionen des Hamiltonoperators 33<br />
Die stationäre Schrödingergleichung<br />
Das Eigenwertproblen Hermitescher Operatoren<br />
Vollständigkeit<br />
Diskretes <strong>und</strong> kontinuierliches Spektrum<br />
3.2 Der harmonische Oszillator 37<br />
Konstruktion <strong>der</strong> Eigenwerte <strong>und</strong> Eigenfunktionen<br />
Interpretation <strong>und</strong> Vergleich mit <strong>der</strong> klassischen Mechanik<br />
Auswahlregeln<br />
3.3 Die Potentialmulde: Diskretes <strong>und</strong> kontinuierliches Spektrum 48<br />
Durchlässikeit <strong>und</strong> Reflexion<br />
Ausstrahlungsbedingung<br />
3.4 Das eindimensionale Kastenpotential 52<br />
3.5 Potentialbarriere <strong>und</strong> Tunneleffekt 58<br />
3.6 Kugelsymmetrische Potentiale im dreidimensionalen Raum 59<br />
Separation <strong>der</strong> Schrödingergleichung<br />
Kugelflächenfunktionen <strong>und</strong> Drehimpuls–Eigenfunktionen<br />
Die Quantenzahlen l <strong>und</strong> m, Richtungsquantelung<br />
Effektives Potential <strong>und</strong> radiale Schrödingergleichung<br />
3.7 Das Wasserstoffatom 67<br />
Haupt– <strong>und</strong> Neben–Quantenzahlen, Entartung<br />
Interpretation <strong>und</strong> Vergleich mit <strong>der</strong> klassischen Mechanik<br />
Selbskonsistenz, das Problem <strong>der</strong> Selbstenergie<br />
4. Mehrteilchensysteme<br />
4.1 Die Schrödingergleichung 74<br />
ii
4.2 Identische Teilchen <strong>und</strong> Spin 75<br />
Die Ununterscheidbarkeit identischer Teilchen<br />
Symmetrische <strong>und</strong> antisymmetrische Wellenfunktionen<br />
Bosonen <strong>und</strong> Fermionen, Pauliprinzip<br />
4.3 Atombau <strong>und</strong> periodisches System <strong>der</strong> Elemente 78<br />
Das Schalenmodell, s–, p–, d– <strong>und</strong> f–Zustände<br />
Hauptgruppen, Nebengruppen, Lanthanoide <strong>und</strong> Aktinoide<br />
4.4 Die Bildung von Molekülen 81<br />
Heteropolare <strong>und</strong> homöopolare Bindung<br />
Das Wasserstoffmolekül, Austauschkraft<br />
5. Die Interpretation <strong>der</strong> <strong>Quantenmechanik</strong><br />
5.1 Der Formalismus 84<br />
Zustandsvektoren <strong>und</strong> Operatoren, Kommutatoren<br />
Darstellungen <strong>und</strong> Bil<strong>der</strong><br />
Heisenbergbild <strong>und</strong> Heisenberggleichung<br />
Eigenwerte <strong>und</strong> Eigenvektoren, Spektrum<br />
Entwicklung nach Eigenvektoren<br />
Bornsche Interpretation<br />
5.2 Meßprozeß <strong>und</strong> Zustandsvektor 87<br />
Die Reproduzierbarkeit <strong>der</strong> Messung<br />
Meßwerte <strong>und</strong> Eigenwerte<br />
Das Problem <strong>der</strong> Entartung<br />
Kommensurable <strong>und</strong> inkommensurable Observable<br />
Die Reduktion des Zustandsvektors<br />
5.3 Das Einstein-Podolsky-Rosen (EPR)–Paradoxon 90<br />
Vollständigkeit einer Theorie<br />
Physikalische Realität<br />
Die störungsfreie Messung<br />
Bohms Version des EPR–Experiments<br />
Die Originalversion des EPR–Experiments<br />
Positivismus <strong>und</strong> Realismus<br />
5.4 Schrödinger <strong>und</strong> seine Katze 94<br />
Korrespondenz zur klassischen Mechanik<br />
Erwartungskatalog <strong>und</strong> Ensembleinterpretation<br />
Empirischer Standpunkt <strong>und</strong> Vollständigkeitspostulat<br />
Der berühmte “burleske Fall”<br />
iii
5.5 Verborgene Parameter <strong>und</strong> Bohms Interpretation 95<br />
Vergleich mit <strong>der</strong> Hamilton–Jakobi–Theorie<br />
Das Quantenpotential<br />
de Broglies Führungswellen<br />
Quantenpotential <strong>und</strong> Kenntnisstand<br />
5.6 Lokalität <strong>und</strong> Bellsche Ungleichung 97<br />
Das Problem <strong>der</strong> Lokalität <strong>und</strong> Separabilität<br />
Konsequenzen des EPR–Experiments<br />
Die Bellsche Ungleichung<br />
<strong>Quantenmechanik</strong> <strong>und</strong> Verschränkung<br />
Literaturhinweise 100<br />
iv
1 Einführung<br />
1.1 Historische Ausgangssituation<br />
Nach<br />
• Kepler, Galilei <strong>und</strong> Newton... (Materie)<br />
• Huygens... (Licht)<br />
• Faraday, Maxwell (Feldbegriff, Elektrodynamik)<br />
• Boltzmann...(Brücke von <strong>der</strong> mikroskopischen zur makroskopischen Physik)<br />
hielt man gegen Ende des 19. Jahrhun<strong>der</strong>ts die Physik im wesentlichen <strong>für</strong> abgeschlossen:<br />
künftige Probleme sah man nur noch in <strong>der</strong> Auswertung bekannter<br />
Gr<strong>und</strong>gesetze unter komplexen Bedingungen.<br />
Allerdings sah Lord Kelvin (* William Thomson 1824) “Zwei kleine dunkle<br />
Wolken” am Horizont.<br />
– Das negative Ergebnis des Versuches von Michelson <strong>und</strong> Morley <strong>und</strong><br />
– die “Ultraviolettkatastrophe” des Rayleigh–Jeansschen Strahlungsgesetzes<br />
u(ν, T ) ∼ ν 2 T.<br />
Diese kleinen dunklen Wolken am Horizont lösten sich nicht auf, son<strong>der</strong>n führten<br />
zu heftigen Gewittern, die die Gr<strong>und</strong>pfosten <strong>der</strong> klassischen Physik erschütterten.<br />
Der negative Ausgang des Michelson–Morley–Experiments führte zur Relativitätstheorie,<br />
die unsere angeborene Anschauung von Raum <strong>und</strong> Zeit ad absurdum<br />
führt (vgl. Raum <strong>und</strong> Zeit bei Newton!).<br />
Noch tiefgreifen<strong>der</strong> erwies sich die Umwälzung durch die zweite dunkle Wolke, die<br />
zur Quantentheorie führte. Die Diskussion um ihre erkenntnistheoretische <strong>und</strong><br />
naturphilosophische Implikation ist bis heute nicht abgeschlossen, die Gr<strong>und</strong>problematik<br />
ist ungeklärt.<br />
Neben <strong>der</strong> erwähnten Ultraviolettkatastrophe gab es weitere experimentelle Erfahrungen,<br />
die zu Gr<strong>und</strong>pfeilern <strong>der</strong> Quantentheorie wurden:<br />
1
• Die spezifische Wärme fester Körper cv ist nach <strong>der</strong> klassischen Theorie<br />
konstant (Dulong–Petitsches Gesetz). Experimentell findet man jedoch,<br />
daß cv <strong>für</strong> T → 0 gegen 0 geht.<br />
• Beim Photoeffekt lassen sich auch bei (fast) beliebig gesteigerter Intensität<br />
nur oberhalb einer Grenzfrequenz Elektronen aus einem Metall auslösen.<br />
• Im Gegensatz zur klassischen Erwartung aus dem Rutherfordschen Atommodell<br />
sind Atome im Gr<strong>und</strong>zustand stabil. “Angeregte” Atome senden<br />
kein kontinuierliches Spektrum, son<strong>der</strong>n diskrete Linienstrahlung aus. Sie<br />
können Energie nur in diskreten “Quanten” aufnehmen (Franck – Hertz).<br />
1.2 Korpuskeleigenschaft des Lichts<br />
Ein Teil dieser seltsamen Resultate (Photoeffekt [Einstein] <strong>und</strong> Hohlraumstrahlung<br />
[Planck]), ließ sich nur verstehen <strong>und</strong> dann sogar quantitativ richtig beschreiben,<br />
wenn man Huygens Erkenntnis <strong>der</strong> Wellennatur des Lichts zumindest<br />
teilweise wie<strong>der</strong> aufgab <strong>und</strong> durch ein Konzept von Teilchen, sogenannten Photonen<br />
(Einstein 1905), mit einer Energie<br />
ersetzte. Dabei ist<br />
E = hν = ¯hω (1)<br />
h = 6.626 · 10 −34 Js bzw. ¯h = h<br />
2π = 1.055 · 10−34 Js (2)<br />
die selbe Konstante, die Planck 1900 <strong>für</strong> sein halbempirisches Strahlungsgesetz 1<br />
u(ν, T ) = 8πν2<br />
c 2<br />
hν<br />
e hν<br />
kT − 1<br />
eingeführt hatte. Durch die Verbindung einer Welleneigenschaft, <strong>der</strong> Frequenz ν,<br />
mit einer Teilchenenergie E trägt (1) bereits den Keim des berühmten “Welle–<br />
Teilchen–Dualismus” in sich. Über E = mc 2 können wir dem Photon eine<br />
Masse m = hν/c 2 zuordnen. Damit erhält das Photon einen Teilchen–Impuls<br />
p = mc = hν<br />
c<br />
= h<br />
λ<br />
(3)<br />
= ¯hk , (4)<br />
<strong>der</strong> mit <strong>der</strong> an<strong>der</strong>en Welleneigenschaft, <strong>der</strong> Wellenlänge λ bzw. <strong>der</strong> Wellenzahl<br />
1 Beachte, daß (3) <strong>für</strong> kleine ν in das Rayleigh–Jeansschen Strahlungsgesetz u → 8πk<br />
übergeht. Statt <strong>der</strong> UV–Katastrophe erhält man <strong>für</strong> große ν die Formel u → 8πhν3<br />
c2 Form bereits Wien (1896) angegeben hatte!<br />
2<br />
c2 ν2T hν − e kT , <strong>der</strong>en
k = 2π<br />
λ<br />
verknüpft ist. Die Verknüpfung erfolgt in beiden Formeln (1) <strong>und</strong> (4) durch das<br />
Plancksche Wirkungsquantum h (bzw. ¯h). Die experimentelle Bestätigung<br />
von Gleichung (4) ergibt sich aus <strong>der</strong> Streuung von Photonen (Röntgenstrahlen)<br />
an Elektronen (Compton–Effekt, 1923).<br />
1.3 Welleneigenschaften <strong>der</strong> Materie<br />
Nicht alle unverstandenen Erfahrungen ließen sich auf Photonen zurückführen.<br />
Zur Erklärung <strong>der</strong> Atomspektren führten Bohr (1913) <strong>und</strong> Sommerfeld (1916)<br />
die Quantenbedingung<br />
<br />
(5)<br />
pdq = nh (6)<br />
<strong>für</strong> periodische Systeme ein. Hierauf fußt die “alte Quantentheorie”, auf die wir<br />
hier nicht näher eingehen. Mit <strong>der</strong> Bedingung (6) ist im “Bohrschen Atommodell”<br />
nur ein diskreter Satz von Elektronenbahnen mit “Energieniveaus” En<br />
erlaubt. Die Spektren erklären sich dann aus <strong>der</strong> Frequenzbedingung<br />
En − Em = hνnm. (7)<br />
Einen wesentlich radikaleren Schritt vollzog de Broglie (Dissertation 1923/24),<br />
indem er die Beziehungen<br />
<strong>und</strong><br />
ν = E/h bzw. E = ¯hω (8)<br />
λ = h/p bzw. p = ¯hk, (9)<br />
die Einstein <strong>für</strong> Photonen postuliert hatte, auf materielle Teilchen wie Elektronen<br />
<strong>und</strong> Protonen übertrug <strong>und</strong> die Vorstellung von Materiewellen entwickelte.<br />
Im Rahmen dieses Wellenbildes läßt sich die Quantenbedingung (6) anschaulich<br />
über stehende Elektronenwellen deuten:<br />
n =<br />
dx<br />
λ<br />
<br />
1<br />
=<br />
h<br />
pdq − +<br />
3
Der Nachweis <strong>der</strong> Wellennatur von Materie gelang Davisson <strong>und</strong> Germer (1927)<br />
durch Interferenzerscheinungen bei <strong>der</strong> Reflexion von Elektronen an Kristallen.<br />
Die Tatsache, daß die Wellennatur <strong>der</strong> Materie länger verborgen blieb als die<br />
des Lichts, liegt an <strong>der</strong> kleinen Wellenlänge, die dem großen Impuls materieller<br />
Teilchen (m0 = 0) entspricht.<br />
1.4 Welle–Teilchen–Dualismus <strong>und</strong> Komplementarität<br />
Sowohl die Materie als auch das Licht zeigen also je nach den experimentellen<br />
Bedingungen entwe<strong>der</strong> Teilchen– o<strong>der</strong> Wellencharakter. Diese komplementären<br />
Beschreibungen sind we<strong>der</strong> in unserer Anschauung noch im Experiment simultan<br />
realisierbar: Je<strong>der</strong> Versuch, den einen Aspekt deutlich herauszuarbeiten, zerstört<br />
den an<strong>der</strong>en <strong>und</strong> umgekehrt. Wir wollen das kurz an einem Doppelspaltexperiment<br />
erläutern: Ein Licht– o<strong>der</strong> Materiestrom falle auf eine Blende B mit Doppelspalt<br />
D1, D2<br />
Auf einem Schirm S hinter <strong>der</strong> Blende beobachten wir die Intensität als Interferenzmuster.<br />
Dieses Interferenzmuster spiegelt die Wellennatur unseres einfallenden<br />
Stromes wie<strong>der</strong>.<br />
Vom Teilchenbild her geht ein Teil <strong>der</strong> Partikel durch D1 <strong>und</strong> ein an<strong>der</strong>er Teil<br />
durch D2. Das Interferenzmuster wird auch dann beobachtet, wenn <strong>der</strong> Teilchenstrom<br />
so reduziert wird, daß nur “selten” jeweils ein Teilchen auf den Schirm<br />
trifft. Eine Wechselwirkung verschiedener Teilchen ist dann ausgeschlossen <strong>und</strong><br />
es liegt nahe, jeweils zu untersuchen, durch welchen <strong>der</strong> beiden Spalte D1 o<strong>der</strong> D2<br />
die Teilchen gehen. Aber je<strong>der</strong> Versuch, eine Entscheidung zwischen D1 o<strong>der</strong> D2<br />
zu treffen zerstört das Interferenzmuster! Beobachte ich also den Teilchenaspekt,<br />
verliert sich <strong>der</strong> Wellenaspekt <strong>und</strong> umgekehrt (Komplementaritätsprinzip).<br />
Ein ganz wichtiger Punkt dabei ist, daß diese Komplementarität nicht auf einer<br />
speziellen Struktur bestimmter Elementarteilchen wie Elektronen o<strong>der</strong> Photonen<br />
beruht, son<strong>der</strong>n ein allgemeines Prinzip darstellt, dem jede physikalische Beobachtung<br />
unterliegt. Mit <strong>der</strong> Betonung des Wortes “Beobachtung” deuten wir bereits<br />
4<br />
B<br />
D 1<br />
D 2<br />
S
hier das (scheinbar) subjektive Element an, das die Quantentheorie in die Physik<br />
gebracht hat: Wir begnügen uns mit <strong>der</strong> mathematischen Beschreibung von<br />
Phänomenen, die wir bei bestimmten Experimenten mit Elektronen o<strong>der</strong> Photonen<br />
beobachten, müssen aber auf Aussagen über das Elektron o<strong>der</strong> Photon (o<strong>der</strong><br />
Stück Kreide?!) an sich verzichten! Genau hier liegt <strong>der</strong> Kern des immer noch<br />
nicht ganz ausgeräumten Gegensatzes zwischen<br />
– POSITIVISMUS (Kopenhagener Schule, Bohr, Heisenberg) <strong>und</strong><br />
– REALISMUS (de Broglie, Schrödinger, Einstein: Än<strong>der</strong>t sich das Weltall,<br />
wenn eine Maus es anschaut?)<br />
Das Komplementaritätsprinzip, das die simultane Bestimmung von Wellen– <strong>und</strong><br />
Teilchenaspekten verbietet, ist eng mit <strong>der</strong> berühmten Unschärferelation verknüpft:<br />
Ich kann nicht gleichzeitig den Teilchenort x <strong>und</strong> die Wellenlänge λ (genau)<br />
messen. Wegen <strong>der</strong> de Broglieschen Beziehung (9) heißt das aber, daß<br />
nicht gleichzeitig <strong>der</strong> Ort <strong>und</strong> <strong>der</strong> Impuls eines Teilchens genau angegeben werden<br />
können. Genau die werden aber als Anfangsbedingungen in <strong>der</strong> klassischen<br />
Mechanik benötigt. Damit bricht also das deterministische Weltbild <strong>der</strong> klassischen<br />
Mechanik gr<strong>und</strong>sätzlich zusammen!<br />
Was bleibt im Teilchenbild, wenn wir den Ort eines Teilchens nicht mehr genau<br />
angeben können? Eine mehr o<strong>der</strong> weniger diffuse Information über die Aufenthaltswahrscheinlichkeit<br />
des Teilchens. [Ebenso entspricht <strong>der</strong> Unkenntnis über den<br />
genauen Impuls eine Wahrscheinlichkeitsverteilung aller möglichen Impulse.]<br />
Wenn wir ins Wellenbild wechseln, so liegt es nahe, die Aufenthaltswahrscheinlichkeit<br />
eines Teilchens mit <strong>der</strong> Intensität, also dem Amplitudenquadrat <strong>der</strong> entsprechenden<br />
Welle zu identifizieren. Die Wahrscheinlichkeitsinterpretation <strong>der</strong> Wellenamplitude<br />
löst auch den Wi<strong>der</strong>spruch zwischen kontinuierlichem Welleneinfall<br />
<strong>und</strong> diskreter Registrierung von Ereignissen auf dem Schirm bei geringer Intensität.<br />
In dieser Wahrscheinlichkeitsinterpretation selbst sind sich zwar die Positivisten<br />
(Kopenhagen) <strong>und</strong> Realisten einig, ihr Hintergr<strong>und</strong> ist aber umstritten: Ist es<br />
wirklich sinnlos nach dem Ort <strong>und</strong> dem Impuls eines Teilchens zu fragen o<strong>der</strong> ist<br />
die Natur nur zu “schamhaft”, uns beide Größen preiszugeben? Sind wir vielleicht<br />
beim Experimentieren (notwendigerweise) so grob, daß wir die komplementäre<br />
Information zerstören? Natürlich kennen wir auch sonst die Störung eines Systems<br />
durch eine Messung, aber innerhalb <strong>der</strong> Gültigkeit <strong>der</strong> klassischen Physik läßt sich<br />
diese Störung im Prinzip beliebig klein machen (o<strong>der</strong> sogar wegrechnen).<br />
In <strong>der</strong> <strong>Quantenmechanik</strong> müssen wir uns dagegen prinzipiell mit einer gewissen<br />
Unkenntnis <strong>und</strong> entsprechenden Wahrscheinlichkeiten begnügen. Für die Positivisten<br />
ist die Physik mit diesen Wahrscheinlichkeiten vollständig beschrieben.<br />
Die Realisten möchten dagegen an einer an sich deterministischen Welt festhalten<br />
(Einstein: Gott würfelt nicht!), akzeptieren dabei aber, daß diese deterministi-<br />
5
sche Welt <strong>für</strong> uns nicht vollständig erfaßbar ist.<br />
Wir werden auf diese <strong>und</strong> ähnliche Fragen noch verschiedentlich zurückkommen,<br />
wenn wir uns in diesem Semester mit <strong>Quantenmechanik</strong> befassen. Damit meinen<br />
wir konkret, daß wir dem Teilchenbild <strong>der</strong> klassischen Mechanik ein Wellenbild<br />
<strong>der</strong> Materie gegenüberstellen, das im Rahmen eines Wahrscheinlichkeitskonzeptes<br />
zu interpretieren ist.<br />
Bevor wir im nächsten Kapitel dieses Programms konkretisieren, stellen wir zunächst<br />
elementares Rüstzeug zur Beschreibung von Wellen <strong>und</strong> zur Beschreibung von<br />
Wahrscheinlichkeiten zusammen.<br />
1.5 Gr<strong>und</strong>begriffe <strong>der</strong> Wellenbeschreibung<br />
Wir betrachten ebene harmonische Wellen <strong>der</strong> Form<br />
bzw.<br />
(a) ψ = cos ϕ, (b) ψ = sin ϕ (10)<br />
(a) ψ = e iϕ , (b) ψ = e −iϕ<br />
(11)<br />
o<strong>der</strong> einer Linearkombination von (a) <strong>und</strong> (b). (Auf die formal o<strong>der</strong> inhaltlich<br />
begründete komplexe Schreibweise wollen wir hier nicht elaborieren.) Über die<br />
Phase<br />
ϕ = kx − ωt bzw. ϕ = k · r − ωt (12)<br />
hängt ψ periodisch von <strong>der</strong> Zeit t <strong>und</strong> vom Ort x (eindimensional) bzw. r (dreidimensional)<br />
ab. ω = 2πν ist die Frequenz <strong>und</strong> k = 2π/λ die Wellenzahl (bzw. k<br />
<strong>der</strong> Wellenvektor) <strong>der</strong> Welle. Punkte x = (ϕ0 + ωt)/k konstanter Phase ϕ0 (z. B.<br />
Wellenberge) bewegen sich mit <strong>der</strong> Phasengeschwindigkeit<br />
vp = ω/k. (13)<br />
Für Licht im Vakuum haben wir bekanntlich vp = c. Licht in Materie hat eine<br />
an<strong>der</strong>e Phasengeschwindigkeit, das Verhältnis c/vp = n wird Brechungsindex<br />
genannt. (Beachte: n < 1 ist nicht verboten!) Än<strong>der</strong>t sich <strong>der</strong> Berechnungindex<br />
bzw. die Phasengeschwindigkeit mit <strong>der</strong> Frequenz bzw. <strong>der</strong> Wellenlänge, spricht<br />
man von Dispersion. Die Beziehung<br />
ω = ω(k), (14)<br />
6
welche die Ausbreitung <strong>der</strong> Welle kontrolliert, wird daher allgemein Dispersionsgleichung<br />
genannt. Sind k o<strong>der</strong> ω dabei komplex, so sind die Wellen räumlich<br />
o<strong>der</strong> zeitlich gedämpft.<br />
Für die konkrete Anschrift einer ebenen Welle bevorzugen wir die Form (11a).<br />
Der Einfachheit halber beschränkten wir uns außerdem soweit als möglich auf<br />
den eindimensionalen Fall (12a). Mit einer (komplexen) Amplitude A schreiben<br />
wir also eine ebene Welle in <strong>der</strong> Form<br />
ψ(x, t) = Ae i(kx−ωt)<br />
(15)<br />
an. Eine solche ebene Welle ist zeitlich wie räumlich unendlich ausgedehnt, ein<br />
langweiliges, strukturloses Phänomen ohne jeden Informationsfluß. Um interessantere<br />
Phänomene wie Licht-Bil<strong>der</strong>, Geräusche <strong>und</strong> Musik darzustellen, benötigen<br />
wir Wellenpakete, die durch Überlagerung verschiedener ebener Wellen entstehen:<br />
<br />
ψ(x, t) = A(k)e i[kx−ω(k)t] dk. (16)<br />
Daß wir mit solchen Überlagerungen räumlich <strong>und</strong>/o<strong>der</strong> zeitlich eng begrenzte<br />
Strukturen erzeugen können (Lichtblitz, Knall), wissen wir aus zahlreichen Erfahrungen.<br />
Wir wollen uns dazu aber auch rechnerisch ein konkretes Beispiel ansehen<br />
<strong>und</strong> betrachten eine Gaußverteilung<br />
A(k) = e − k2l 2<br />
2<br />
<strong>der</strong> Amplituden mit einer Breite ∆k ∼ 1/l um k = 0. Dann hat die Welle zur<br />
Zeit t = 0 die räumliche Struktur<br />
<br />
ψ(x, 0) =<br />
e − k2l 2<br />
2 +ikx x2<br />
−<br />
dk = e 2l2 <br />
x2<br />
−<br />
= e 2l2 <br />
x2<br />
−<br />
= e 2l2 <br />
e −<br />
k 2 l 2<br />
e −<br />
<br />
√2<br />
kl<br />
−i x<br />
2 √<br />
2l dk<br />
e − k2l 2<br />
√<br />
2π x2<br />
−<br />
2 dk = e 2l<br />
l<br />
2<br />
2<br />
x2<br />
−ikx−<br />
2l2 <br />
dk<br />
Dies ist wie<strong>der</strong> eine Gaußverteilung, <strong>und</strong> zwar um x = 0 mit einer Breite ∆x ∼ l.<br />
Je schmaler wir also die k-Verteilung wählen, um so breiter wird die x-Verteilung<br />
<strong>und</strong> umgekehrt; <strong>und</strong> daß das Produkt<br />
7
∆k · ∆x ∼ 1 (17)<br />
an die Unschärferelation erinnert, ist gewiß kein Zufall: Man kann nicht gleichzeitig<br />
den Ort <strong>und</strong> die Wellenlänge eines Wellenpakets scharf angeben. (Für an<strong>der</strong>e<br />
Verteilungen als Gaußglocken wird das Unschärfeprodukt sogar noch größer.)<br />
Ebensowenig läßt sich die Zeit <strong>und</strong> die Frequenz eines Wellenpakets simultan<br />
angeben, denn wir erhalten ein entsprechendes Unschärfeprodukt<br />
∆ω∆t ∼ 1 (18)<br />
(o<strong>der</strong> noch größer): Ein Ton mit sauber definierter Tonhöhe muß lange andauern,<br />
ein Ton zu kurzer Dauer ist kein Ton mehr, son<strong>der</strong>n ein Knall.<br />
Wenn das Medium dispersionsfrei ist, wenn also die Phasengeschwindigkeit vp =<br />
ω/k konstant ist, breitet sich unser Wellenpaket (16) unverzerrt mit konstanter<br />
Geschwindigkeit vp aus. Denn wir erhalten mit ξ = x − vpt aus (16)<br />
<br />
ψ(x, t) = A(k)e ikξ dk = ψ(ξ, 0) = ψ(x − vpt, 0).<br />
In einem Medium mit Dispersion dagegen breiten sich die verschiedenen Komponenten<br />
des Wellenpakets verschieden schnell aus <strong>und</strong> das Paket “zerläuft”<br />
allmählich. Wenn jedoch die k–Verteilung hinreichend eng um die Wellenzahl<br />
k0 liegt, erfolgt dieses Zerlaufen sehr langsam <strong>und</strong> wir können vorher noch sinnvoll<br />
nach <strong>der</strong> Ausbreitung des Wellenpakets fragen. Nehmen wir also an, daß<br />
A(k0 + κ) = a(κ) nur <strong>für</strong> kleine κ von Null verschieden ist. Dann folgt aus (16)<br />
ψ(x, t) = e i(k0x−ω0t)<br />
<br />
a(κ)e iκ<br />
<br />
x− ∂ω<br />
<br />
∂k | t<br />
k0 dκ<br />
= e i(k0x−ω0t)<br />
<br />
f x − ∂ω<br />
<br />
<br />
<br />
<br />
∂k<br />
<br />
t mit ω0 = ω(k0).<br />
Die Welle läßt sich also als ebene Trägerwelle<br />
mit einem Modulations–Faktor<br />
beschreiben:<br />
e i(k0x−ω0t)<br />
<br />
f x − ∂ω<br />
<br />
<br />
<br />
<br />
∂k<br />
8<br />
k0<br />
k0<br />
t
1.0<br />
0.5<br />
0.0<br />
−0.5<br />
f e i(k 0 x−ωt)<br />
−1.0<br />
−3.0 −2.0 −1.0 0.0 1.0 2.0 3.0<br />
Während die Trägerwelle die Phasengeschwindigkeit ω0/k0 aufweist, bewegt sich<br />
<strong>der</strong> Modulationsfaktor — also <strong>der</strong> Bereich, in dem die Welle eine merkliche Amplitude<br />
aufweist — mit <strong>der</strong> Gruppengeschwindigkeit<br />
vg = ∂ω<br />
∂k<br />
x<br />
(19)<br />
durch den Raum. Im Gegensatz zu <strong>der</strong> strukturlosen, langweiligen Trägerwelle<br />
beinhaltet <strong>der</strong> Modulationsfaktor f die gesamte interessante Information o<strong>der</strong> das<br />
Signal. vg wird daher auch Signalgeschwindigkeit genannt. Sie ist eine physikalisch<br />
signifikante Größe <strong>und</strong> kann — im Gegensatz zu vp — nie die Lichtgeschwindigkeit<br />
überschreiten.<br />
1.6 Gr<strong>und</strong>begriffe <strong>der</strong> Wahrscheinlichkeitsrechnung<br />
Wir ordnen irgendwelchen möglichen Ereignissen A Wahrscheinlichkeiten p(A) zu<br />
<strong>und</strong> verstehen darunter die relative Häufigkeit<br />
p(A) = lim<br />
n→∞<br />
nA<br />
, (20)<br />
n<br />
mit <strong>der</strong> das Ereignis A bei vielen (n → ∞) unabhängigen Versuchen unter gleichen<br />
Bedingungen auftritt (Beispiel: p (3 Augen) = 1/6 beim Würfeln). Die intuitive<br />
Anschauung faßt man mathematisch im Kolmogorovschen Axiomensystem<br />
2 zusammen, aus dem man Rechenregeln wie<br />
p(A ∨ B) = p(A) + p(B) − p(A ∧ B) (21)<br />
p(¬A) = 1 − p(A) (22)<br />
2 Ereignisse A ⊂ Ω, p(A) : P(Ω) → R mit (i) p(A) ≥ 0, (ii) p(A ∪· B) = p(A) +<br />
p(B) <strong>und</strong> (iii) p(Ω) = 1.<br />
9
ableitet. Solche Rechenregeln benutzt man auch, um Wahrscheinlichkeiten <strong>für</strong><br />
Ereignisse zu formulieren, die man nicht durch die relative Häufigkeit bei vielen<br />
Versuchen ermitteln kann. (Beispiel: p <strong>für</strong> den GAU eines Atomkraftwerkes).<br />
Ereignisse A <strong>und</strong> B sind nicht notwendigerweise unabhängig voneinan<strong>der</strong>. Man<br />
nennt<br />
p(A ∧ B)<br />
p(A|B) :=<br />
p(B)<br />
(23)<br />
die “bedingte Wahrscheinlichkeit <strong>für</strong> A, wenn B vorliegt”. Sind A <strong>und</strong> B unabhängig,<br />
ist p(A|B) = p(A), also gilt<br />
p(A ∧ B) = p(A)p(B). (24)<br />
Bestehen die (Elementar–)Ereignisse Ai darin, daß eine Variable x die Werte<br />
xi annimmt, nennt man x eine Zufallsvariable. Ist <strong>der</strong> Satz xi möglicher Werte<br />
abzählbar, sprechen wir von einer diskreten Zufallsvariable. Da<strong>für</strong> gilt<br />
<br />
p(xi) = 1. (25)<br />
i<br />
Ist die Zufallsvariable kontinuierlich, müssen wir differentielle Wahrscheinlichkeiten<br />
p(x)dx mit<br />
<br />
p(x)dx = 1 (26)<br />
betrachten. Abweichend von <strong>der</strong> Bezeichnung in <strong>der</strong> Mathematik ist es in <strong>der</strong><br />
Physik üblich, p(x) als Verteilungsfunktion zu bezeichnen. Wir werden nicht immer<br />
sauber zwischen <strong>der</strong> Anschrift (25) <strong>und</strong> (26) unterscheiden <strong>und</strong> daher beide<br />
Ausdrücke ggf. sinngemäß umdeuten. Das gilt insbeson<strong>der</strong>e <strong>für</strong> den Mischfall,<br />
in dem eine Zufallsvariable bestimmte diskrete <strong>und</strong> bestimmte kontinuierliche<br />
Werte annehmen kann (Beispiel: Energie eines Atoms). Wollen wir die jeweils<br />
sinngemäße Interpretation betonen, schreiben wir auch<br />
<br />
p(x)dx = 1. (27)<br />
Natürlich kann eine Zufallsvariable auch mehrdimensional sein. Dabei denken wir<br />
z. B. an den Ort r <strong>und</strong> verstehen (25)–(27) dann entsprechend als<br />
Mit <strong>der</strong> Verteilungfunktion definieren wir Mittelwerte<br />
<br />
p(r)d 3 r = 1 usw. (28)<br />
10
Die speziellen Mittelwerte<br />
¯f = 〈f(x)〉 = <br />
f(x)p(x)dx. (29)<br />
〈x n 〉 = <br />
x n p(x)dx (30)<br />
heißen auch “Momente” <strong>der</strong> Verteilungsfunktion. Neben dem ersten Moment –<br />
〈x〉, das den Mittelwert <strong>der</strong> Zufallsvariable angibt, ist insbeson<strong>der</strong>e das zweite<br />
Moment 〈x 2 〉 von Bedeutung. Mit ihm erhält man die Varianz<br />
(∆x) 2 = 〈(x − 〈x〉) 2 〉 = 〈x 2 〉 − 〈x〉 2 , (31)<br />
welche die “Breite” <strong>der</strong> Verteilung repräsentiert.<br />
Wie im Abschnitt 1.4 andiskutiert, wollen wir im folgenden das Amplitudenquadrat<br />
von Materiewellen als Aufenthaltswahrscheinlichkeit eines Teilchens interpretieren.<br />
Da wir unsere Wellen komplex ausschreiben wollen <strong>und</strong> p ≥ 0 gelten<br />
muß, heißt das präzise, daß wir eine Wahrscheinlichkeitsverteilung<br />
p(r, t) = ψ ∗ (r, t)ψ(r, t) (32)<br />
postulieren. Gemäß (28) muß die Wellenamplitude also die Nebenbedingung<br />
<br />
ψ ∗ (r, t)ψ(r, t)d 3 r = 1 (33)<br />
erfüllen. Irgendwelche Ortsfunktionen f(r) haben dann nach (29) den Mittelwert<br />
<br />
¯f(t) =<br />
ψ ∗ (r, t)f(r)ψ(r, t)d 3 r. (34)<br />
11
2 Die Schrödingergleichung<br />
2.1 Entwicklung <strong>der</strong> Wellengleichung<br />
Gemäß unserer Vorbesprechung möchten wir nun eine Wellengleichung aufstellen,<br />
welche die Ausbreitung <strong>der</strong> Materiewellen beschreibt. Dabei sollten wir uns<br />
von vornherein klar darüber sein, daß wir die Wellengleichung nicht “herleiten”<br />
können – ebensowenig wie irgendeine an<strong>der</strong>e Gr<strong>und</strong>gleichung <strong>der</strong> Physik.<br />
Vielmehr geht es darum, die Gr<strong>und</strong>postulate durch mehr o<strong>der</strong> weniger plausible<br />
Ansätze zu erfüllen. Diese Ansätze werden dann im Laufe <strong>der</strong> Zeit durch Vergleich<br />
von Theorie <strong>und</strong> Experiment erhärtet o<strong>der</strong> wi<strong>der</strong>legt.<br />
Bezüglich <strong>der</strong> Gr<strong>und</strong>gleichung <strong>für</strong> Materiewellen tappen wir beson<strong>der</strong>s im Dunkeln,<br />
da wir <strong>der</strong> Wellenfunktion selbst keine direkte physikalische Bedeutung zumessen<br />
3 . Wir wissen lediglich, daß Interferenz auftreten kann. Darum schließen<br />
wir auf ein Superpositionsprinzip <strong>und</strong> for<strong>der</strong>n eine lineare Gleichung.<br />
Weiter wollen wir uns vom Korrespondenzprinzip (Bohr 1923) leiten lassen, nach<br />
dem zwischen klassischen <strong>und</strong> quantenmechanischen Größen eine enge Entsprechung<br />
mit mehr o<strong>der</strong> weniger analogen Beziehungen besteht. (Eine solche Korrespondenz<br />
wird sich allerdings weitgehend erst nachträglich überprüfen lassen).<br />
Schließlich müssen wir bei <strong>der</strong> Formulierung einer Wellengleichung natürlich die<br />
gr<strong>und</strong>legenden Beziehungen (8),(9)<br />
im Auge behalten.<br />
E = ¯hω <strong>und</strong> p = ¯hk<br />
Die uns am meisten vertraute Wellengleichung <strong>der</strong> Form<br />
mit konstantem γ ist nicht geeignet:<br />
∂2ψ ∂t2 = γ ∂2ψ ∂x2 – im Gegensatz zur klassischen Mechanik kann die Lösung nicht durch Anfangsbedingungen<br />
festgelegt werden, da die Gleichung zweiter Ordnung in<br />
<strong>der</strong> Zeit ist<br />
– Der Lösungsansatz e i(kx−ωt) führt auf die Dispersionsgleichung<br />
3 Darum lassen wir auch von vornherein komplexe Wellenfunktionen zu!<br />
12
γ = ω 2 /k 2 = E 2 /p 2<br />
eines dispersionsfreien Mediums mit einer Wellengeschwindigkeit √ γ = E/p, die<br />
von den Anfangsbedingungen abhängt <strong>und</strong> nicht mit <strong>der</strong> Teilchengeschwindigkeit<br />
übereinstimmt.<br />
Nach dem Korrespondenzprinzip erwarten wir, daß die Gruppengeschwindigkeit<br />
vg <strong>der</strong> klassischen Teilchengeschwindigkeit entspricht. Für ein kräftefreies Teilchen<br />
im konstanten Potential V0 gilt E = p 2 /2m + V0. Das entspricht einer Dispersionsbeziehung<br />
¯hω = ¯h2<br />
Die Gruppengeschwindigkeit<br />
2m k2 + ¯hω0 mit ω0 = V0<br />
¯h<br />
vg = ∂ω<br />
∂k<br />
¯h p<br />
= k =<br />
m m<br />
. (35)<br />
(36)<br />
stimmt damit tatsächlich mit <strong>der</strong> Teilchengeschwindigkeit überein. Eine entsprechende<br />
Differentialgleichung, die mit dem Ansatz ψ ∼ e i(kx−ωt) übereinstimmt,<br />
erhalten wir durch die Übersetzung<br />
k → 1<br />
i<br />
∂<br />
∂x<br />
p → ¯h<br />
i<br />
i¯h ∂ψ<br />
∂t<br />
∂<br />
∂x<br />
<strong>und</strong> ω → i ∂<br />
∂t<br />
<strong>und</strong> E → i¯h ∂<br />
∂t<br />
o<strong>der</strong> (37)<br />
(38)<br />
¯h2 ∂<br />
= −<br />
2m<br />
2ψ ∂x2 + V0ψ (39)<br />
Diese Gleichung ist — wie gewünscht — erster Ordnung <strong>und</strong> führt <strong>für</strong> freie Teilchen<br />
auf die erwartete Gruppengeschwindigkeit. Es erhebt sich allerdings die Frage,<br />
wie man sie auf Teilchen in einem konservativem Kraftfeld überträgt. Wenn<br />
wir V0 durch V (x) ersetzen, können wir (35) nicht mehr als Dispersionsgleichung<br />
interpretieren. Tatsächlich können wir ja im Kraftfeld auch keine ebenen Wellen<br />
ψ ∼ e i(kx−ωt) mehr als Lösung erwarten, denn festes k entspricht einem konstanten<br />
Impuls p = ¯hk. Aber auch wenn k keine direkte Bedeutung als Wellenzahl<br />
mehr hat, können wir versuchen, an <strong>der</strong> Übersetzungsvorschrift (38) festzuhalten.<br />
Korrespondierend zu <strong>der</strong> klassischen Beziehung<br />
E = H(p, x) = p2<br />
+ V (x)<br />
2m<br />
13
verallgemeinern wir daher (39) zur eindimensionalen Schrödingergleichung<br />
i¯h ∂ψ<br />
∂t<br />
= − ¯h2<br />
2m<br />
∂2ψ + V (x). (40)<br />
∂x2 Die weitere Verallgemeinerung auf drei Raumdimensionen ist fast trivial: Statt<br />
(40) gehen wir von <strong>der</strong> Übersetzungsvorschrift<br />
p → ¯h<br />
∂<br />
∇ <strong>und</strong> E → i¯h<br />
i ∂t<br />
(41)<br />
aus, wobei <strong>der</strong> Nabla–Operator ∇ die Gradientenbildung bezeichnet. Mit dem<br />
Laplace–Operator ∆ = ∇ 2 erhalten wir dann die dreidimensionale Schrödingergleichung<br />
i¯h ∂ψ<br />
∂t<br />
¯h2<br />
= − ∆ψ + V (r)ψ . (42)<br />
2m<br />
Dies ist die gesuchte Wellengleichung, die Schrödinger 1926 vorgeschlagen <strong>und</strong><br />
die sich in jahrzehntelanger Erfahrung bewährt hat. Bevor wir uns mit dieser<br />
Feststellung zufrieden geben dürfen, müssen wir aber noch zwei wichtige Postulate<br />
nachweisen:<br />
1. Die Erhaltung <strong>der</strong> Nebenbedingung (33) <strong>und</strong><br />
2. <strong>der</strong> Bezug zur klassischen Bewegungsgleichung.<br />
Diese Nachweise werden wir in den Abschnitten 2.3 <strong>und</strong> 2.5 führen. Zuvor wollen<br />
wir uns noch mit einigen formalen Aspekten befassen.<br />
2.2 Formale Eigenschaften <strong>der</strong> Schrödingergleichung<br />
Im Gegensatz zu den Gr<strong>und</strong>gleichungen <strong>der</strong> klassischen Physik ist die Schrödingergleichung<br />
(42) <strong>und</strong> damit die ψ–Funktion wesentlich komplex. Bisher kannten<br />
wir komplexe Anschriften (wie etwa e iϕ = cos ϕ + i sin ϕ o<strong>der</strong> Z = R + iωL)<br />
lediglich als bequeme Zusammenfassung von Beziehungen, in denen Real– <strong>und</strong><br />
Imaginärteil ihre eigene physikalische Bedeutung haben. Die Wellenfunktion ist<br />
dagegen von vornherein komplex, ohne daß Re(ψ) o<strong>der</strong> Im(ψ) eine selbständige<br />
Bedeutung hätten: Eine physikalische Bedeutung hat erst die reelle Größe<br />
p = ψ ∗ ψ.<br />
In <strong>der</strong> Theorie kann ψ auch völlig äquivalent durch ψ ∗ ersetzt werden. ψ ∗ aber<br />
erfüllt nicht die Schrödingergleichung (42), son<strong>der</strong>n die natürlich ebenso äquivalente<br />
konjugiert–komplexe Schrödingergleichung<br />
14
i¯h ∂ψ∗<br />
∂t<br />
= + ¯h2<br />
2m ∆ψ∗ − V (r)ψ ∗ . (43)<br />
An<strong>der</strong>s als wir es sonst von Wellengleichungen gewöhnt sind, sind (mit ϕ =<br />
k · r−ωt) also nicht die vier Funktionen (10a,b) <strong>und</strong> (11a,b) Lösungen <strong>der</strong> kräftefreien<br />
Schrödingergleichung, son<strong>der</strong>n allein <strong>der</strong> Ansatz (11a), von dem wir bei <strong>der</strong><br />
Konstruktion ausgegangen sind. (Der äquivalente Ansatz (11b) führt eben zur<br />
konjugiert–komplexen Schrödingergleichung).<br />
Ohne die imaginäre Einheit i vor <strong>der</strong> Zeitableitung wäre die Schrödingergleichung<br />
als “parabolische Differentialgleichung” ja auch keine Wellengleichung, son<strong>der</strong>n<br />
eine Diffusionsgleichung, <strong>der</strong>en Typ vielleicht von <strong>der</strong> Wärmeleitungsgleichung<br />
∂T<br />
∂t<br />
= κ∆T + f(T )<br />
am ehesten vertraut ist. Mit <strong>der</strong> Diffusionsgleichung hat die Schrödingergleichung<br />
daher gemein, daß ihre Lösung durch Anfangsbedingungen zur Zeit t = 0 festgelegt<br />
ist. Während jedoch die Diffusionsgleichungen zu exponentiell abklingenden<br />
Lösungen ∼ e −t/τ “neigen”, sind <strong>für</strong> die Schrödingergleichung (wegen des i vor<br />
<strong>der</strong> Zeitableitung) oszillierende Lösungen ∼ e −iωt typisch.<br />
Diese Oszillationen von ψ darf man sich freilich ebensowenig als physikalische<br />
Realität vorstellen wie ψ selbst. Hängt ihre Frequenz ω doch von <strong>der</strong> willkürlichen<br />
Wahl des Potential–Nullpunkts ab. In Übereinstimmung damit ist <strong>der</strong> gesamte<br />
Phasenfaktor e −iωt <strong>der</strong> Beobachtung nicht zugänglich, er fällt ja bei <strong>der</strong> Bildung<br />
von ψ ∗ ψ auch heraus! [Beobachtbar sind einzig Phasendifferenzen (Interferenz!);<br />
diese hängen allerdings auch nicht vom Potential–Nullpunkt ab.]<br />
Ebenso wenig — <strong>und</strong> das ist vielen Leuten nicht hinreichend bewußt! — besitzt<br />
die Wellenlänge λ = 2π¯h/p eine Bedeutung, die man dem Teilchen selbst zuordnen<br />
kann. Denn <strong>der</strong> Impuls hängt ja wesentlich von <strong>der</strong> speziellen Wahl des<br />
Bezugssystems ab. Wenn wir in Interferenzexperimenten eine bestimmte Wellenlänge<br />
beobachten, so bezieht sich diese Beobachtung auf ein System, in dem<br />
das Beugungsgitter <strong>und</strong> <strong>der</strong> Schirm ruhen. In diesem System (<strong>und</strong> erst hier!) sind<br />
Impuls <strong>und</strong> Wellenlänge eindeutig festgelegt. Wir nutzen diese Überlegung, um<br />
erneut darauf hinzuweisen, daß wir mit <strong>der</strong> <strong>Quantenmechanik</strong> nicht ein Teilchen,<br />
son<strong>der</strong>n die mögliche Beobachtung eines Teilchens beschreiben. Diese hängt z. B.<br />
vom Teilchen <strong>und</strong> vom Beugungsgitter ab.<br />
2.3 Die Kontinuitätsgleichung<br />
Wir hatten bereits darauf hingewiesen, daß die Wahrscheinlichkeitsinterpretation<br />
(32)<br />
15
p(r, t) = ψ ∗ (r, t)ψ(r, t)<br />
<strong>der</strong> Wellenamplitude verlangt, daß die Normierung (33)<br />
<br />
p(r, t)d 3 <br />
r =<br />
ψ ∗ (r, t)ψ(r, t)d 2 r = 1<br />
im Laufe <strong>der</strong> Zeit erhalten bleibt. Dazu rechnen wir unter Verwendung <strong>der</strong> Schrödingergleichungen<br />
(42) <strong>und</strong> (43)<br />
∂p<br />
∂t<br />
∂ψ<br />
= ψ∗<br />
∂t<br />
= 1<br />
<br />
i¯h<br />
+ ψ ∂ψ∗<br />
∂t<br />
− ¯h2<br />
2m ψ∗ ∆ψ + V ψψ ∗ + ¯h2<br />
2m ψ∆ψ∗ − V ψψ ∗<br />
= i¯h<br />
2m {ψ∗ ∇ · ∇ψ − ψ∇ · ∇ψ ∗ }<br />
= i¯h<br />
2m ∇ · {ψ∗ ∇ψ − ψ∇ψ ∗ } − i¯h<br />
2m {∇ψ∗ · ∇ψ − ∇ψ · ∇ψ ∗ } .<br />
Die letzte Klammer verschwindet <strong>und</strong> wir erhalten die Kontinuitätsgleichung<br />
∂p<br />
∂t<br />
+ div S = 0 mit (44)<br />
p(r, t) = ψ ∗ ψ <strong>und</strong> S(r, t) = ¯h<br />
2im {ψ∗ ∇ψ − ψ∇ψ ∗ } .<br />
Die Form <strong>der</strong> Kontinuitätsgleichung stellt die postulierte Erhaltung <strong>der</strong> Normierung<br />
sofort sicher. Denn nach dem Gaußschen Satz gilt<br />
<br />
d<br />
dt<br />
pd 3 r =<br />
<br />
∂p<br />
∂t d3 <br />
r = −<br />
div Sd 3 <br />
r = −<br />
<br />
S · do = 0.<br />
Das Oberflächenintegral verschwindet, da ψ <strong>für</strong> r → ∞ hinreichend stark gegen<br />
Null gehen muss, damit die Normierung überhaupt existiert.<br />
Aus <strong>der</strong> Kontinuitätsgleichung folgern wir weiter, daß S(r, t) eine Wahrscheinlichkeitsstrom-Dichte<br />
beschreibt. Dabei überzeugt man sich leicht, daß S(r, t) —<br />
wie es <strong>für</strong> physikalisch interpretierbare Größen sein muss — tatsächlich reell ist,<br />
denn es gilt nach (44)<br />
S(r, t) = Re[ ¯h<br />
im ψ∗ ∇ψ]. (45)<br />
16
Wir können uns die zeitliche Entwicklung <strong>der</strong> Wahrscheinlichkeitsverteilung also<br />
bildhaft als Strömung einer Flüssigkeit vorstellen. Diese Strömung besitzt we<strong>der</strong><br />
Quellen noch Senken, <strong>und</strong> das garantiert die Erhaltung <strong>der</strong> Normierung.<br />
Wenn wir unsere Beobachtung an hinreichend vielen (N → ∞) unabhängigen<br />
Teilchen durchführen, erwarten wir aufgr<strong>und</strong> <strong>der</strong> Definition <strong>der</strong> Wahrscheinlichkeit<br />
im Abschnitt 1.6 (vgl. Gleichung (20)) im Volumenelement d 3 r<br />
n(r, t) d 3 r = Np(r, t) d 3 r = Nψ ∗ (r, t)ψ(r, t) d 3 r (46)<br />
Teilchen anzutreffen. n(r, t) wird dabei als Teilchendichte bezeichnet. Entsprechend<br />
wird dann<br />
j(r, t) = NS(r, t) = ¯hN<br />
2im {ψ∗ ∇ψ − ψ∇ψ ∗ } (47)<br />
die Teilchenstrom–Dichte <strong>und</strong> die Kontinuitätsgleichung erhält die vertraute<br />
Form<br />
∂n<br />
+ div j = 0.<br />
∂t<br />
(48)<br />
Ebenso kann man durch<br />
ϱm = mn(r, t) <strong>und</strong> ϱe = en(r, t) (49)<br />
eine Massendichte ϱm <strong>und</strong> eine elektrische Ladungsdichte ϱe einführen. Diesen<br />
Dichten entspricht dann die Massenstromdichte bzw. elektrische Stromdichte<br />
<strong>und</strong> es gelten entsprechende Kontinuitätsgleichungen<br />
jm = mj bzw. je = ej, (50)<br />
∂ϱm,e<br />
∂t + div jm,e = 0. (51)<br />
Um die Anschrift solcher Größen noch bequemer zu gestalten, kann man die<br />
entsprechenden Faktoren N, m bzw. e natürlich auch direkt in die Wellenfunktion<br />
aufnehmen. So ist es insbeson<strong>der</strong>e weit verbreitet, statt mit ψ direkt mit<br />
mit <strong>der</strong> Normierung<br />
Ψ(r, t) = √ Nψ(r, t) (52)<br />
17
zu arbeiten. Dann erhält man die Teilchendichte<br />
<strong>und</strong> die Teilchenstrom–Dichte<br />
<br />
ΨΨ ∗ d 3 r = N (53)<br />
n(r, t) = Ψ ∗ Ψ (54)<br />
j(r, t) = ¯h<br />
2im {Ψ∗ ∇Ψ − Ψ∇Ψ ∗ } . (55)<br />
Wegen dieser trivialen Umrechnungen werden wir uns — wie viele Lehrbücher —<br />
im folgenden auch gelegentlich einer bequemen, weniger präzisen Ausdrucksweise<br />
bedienen <strong>und</strong> ψ ∗ ψ kurz als Teilchendichte <strong>und</strong> S = ¯h<br />
2im (ψ∗ ∇ψ − ψ∇ψ ∗ ) kurz als<br />
Stromdichte bezeichnen.<br />
Wichtig ist dabei lediglich, daß wir uns <strong>der</strong> präzisen Bedeutung bewußt bleiben:<br />
Die Interpretation einer Teilchen– <strong>und</strong> einer Stromdichte setzt viele unabhängige<br />
Teilchen voraus. Wir sollten uns daher hüten, uns ein einzelnes Teilchen – etwa<br />
das Elektron im H–Atom – als ausgeschmierte Wolke mit einer Dichteverteilung,<br />
die durch ψ ∗ ψ beschrieben wird, vorzustellen. Diese gr<strong>und</strong>falsche Vorstellung wird<br />
lei<strong>der</strong> in manchen Schulbüchern <strong>der</strong> Physik durch entsprechende Bil<strong>der</strong> suggestiv<br />
unterstützt.<br />
2.4 Erwartungswerte <strong>und</strong> Operatoren<br />
Während wir die Dynamik klassischer Systeme deterministisch beschreiben, müssen<br />
wir uns in <strong>der</strong> <strong>Quantenmechanik</strong> mit einer Angabe <strong>der</strong> Wahrscheinlichkeitsverteilung<br />
begnügen. Wir können daher nicht mehr den Zahlwert dynamischer Variablen<br />
präzise angeben. Um trotzdem die Terminologie <strong>und</strong> anschauliche Vorstellung<br />
soweit wie möglich beibehalten zu können, vergleichen wir den klassischen<br />
Wert einer Variablen f mit ihrem quantenmechanischen Erwartungswert ¯ f o<strong>der</strong><br />
〈f〉. Darunter verstehen wir den in Gl. (34) definierten Mittelwert<br />
<br />
¯f = 〈f〉 =<br />
ψ ∗ (r, t)f(r)ψ(r, t)d 3 r.<br />
Nun sind dynamische Variable aber im allgemeinem nicht allein Funktionen des<br />
Ortes, son<strong>der</strong>n Funktionen von Ort <strong>und</strong> Impuls (Beispiel: E = p 2 /2m + V (r)).<br />
Wie definieren o<strong>der</strong> berechnen wir sinnvoll den Erwartungswert des Impulses?<br />
Für freie Teilchen mit vorgegebenem Impuls p hatten wir den Zusammenhang<br />
p = ¯hk zwischen Impuls <strong>und</strong> Wellenzahl postuliert. Aus <strong>der</strong> Anschrift<br />
18
e i(k·r−ωt)<br />
einer ebenen Welle erhalten wir die Wellenzahl durch Gradientenbildung, −i∇ →<br />
k. Dem entspricht das (rückwärts gelesene) Ersetzungsschema<br />
¯h<br />
∇ → p (56)<br />
i<br />
von Gl. (41). Wir können die beiden Pfeilrichtungen in (41) <strong>und</strong> (56) zu einer<br />
Äquivalenz zusammenfassen, indem wir den Impulsoperator<br />
ˆp = ¯h<br />
∇ (57)<br />
i<br />
einführen. Damit liegt es nahe, den Erwartungswert des Impulses durch<br />
<br />
¯p = 〈ˆp〉 =<br />
ψ ∗ ˆpψd 3 r = ¯h<br />
i<br />
<br />
ψ ∗ ∇ψd 3 r (58)<br />
anzugeben. Für eine ebene Welle 4 ∼ e i(k·r−ωt) mit scharf definiertem Impuls<br />
p = ¯hk stimmt dieser Erwartungswert nach Konstruktion mit dem Impuls überein.<br />
Allgemein stellen wir uns vor, daß wir durch die Differentiation in (58) die<br />
Impulse bilden, die bestimmten Anteilen <strong>der</strong> Wellenfunktion entsprechen, <strong>und</strong><br />
anschließend durch die Integration entsprechend gewichten 5 . Zur Stützung dieser<br />
Argumentation zeigen wir, daß Gl. (58) tatsächlich eine reelle Größe definiert.<br />
Mit<br />
folgt nämlich<br />
¯p ∗ = − ¯h<br />
i<br />
<br />
ψ∇ψ ∗ d 3 r (59)<br />
¯p ∗ <br />
− ¯p = i¯h (ψ ∗ ∇ψ + ψ∇ψ ∗ )d 3 r (60)<br />
<br />
= i¯h<br />
∇(ψ ∗ ψ)d 3 r = 0.<br />
Ausgehend von (57) können wir auch einen Operator<br />
ˆp 2 = −¯h 2 ∇ 2 = −¯h 2 ∆<br />
4 Auf die Frage <strong>der</strong> Normierung ebener Wellen gehen wir später ein. Im Augenblick denken<br />
wir an fast unendlich ausgedehnte Wellenpakete mit fast scharf definiertem Impuls.<br />
5 Eine saubere Begründung läßt sich über eine Fouriertransformation <strong>der</strong> Wellenfunktion<br />
gewinnen. Wir verzichten jedoch darauf.<br />
19
ilden. Auch er führt zu reellen Erwartungswerten, denn es gilt<br />
¯p 2 − ¯ p2∗ = −¯h 2<br />
<br />
(ψ ∗ ∆ψ − ψ∆ψ ∗ )d 3 r<br />
= −¯h 2<br />
<br />
∇ · {ψ ∗ ∇ψ − ψ∇ψ ∗ }d 3 r = 0<br />
(vgl. Rechnung zu Gl.(44) o<strong>der</strong> den Greenschen Satz 6 ). Damit können wir insbeson<strong>der</strong>e<br />
den Hamiltonoperator<br />
bilden.<br />
ˆH = ˆp2<br />
2m + V (r) = −¯h2 ∆<br />
+ V (r) (61)<br />
2m<br />
Allgemeiner läßt sich zeigen, daß nicht nur ˆp <strong>und</strong> ˆp 2 son<strong>der</strong>n alle Potenzen ˆp n zu<br />
reellen Erwartungswerten führen. Das ist kein Zufall, son<strong>der</strong>n es beruht darauf,<br />
daß <strong>der</strong> Operator ˆp selbstadjungiert o<strong>der</strong> hermitesch ist 7 . Über die Potenzreihe<br />
läßt sich diese Eigenschaft schließlich auf alle analytischen Funktionen g(ˆp)<br />
übertragen.<br />
Generell verstehen wir unter einem Operator  eine mathematische Vorschrift,<br />
die aus einer (Wellen–)Funktion ψ eine an<strong>der</strong>e Funktion ϕ erzeugt:<br />
ϕ(r, t) = Âψ(r, t).<br />
Eine triviale Operation in diesem Sinne ist die Multiplikation mit einer Funktion<br />
f(r). Ist f(r) reell, so erhalten wir reelle Erwartungswerte ¯ f, <strong>und</strong> f repräsentiert<br />
einen hermiteschen Operator ˆ f. Insbeson<strong>der</strong>e <strong>der</strong> Ortsoperator ˆr = r selbst ist<br />
hermitesch. Korrespondierend zu irgendwelchen dynamischen Variablen A(r, p)<br />
<strong>der</strong> klassischen Mechanik können wir nun quantenmechanische Operatoren<br />
 = A(r, ˆp) (62)<br />
bilden, die nach den selben Rechenregeln gebildet werden (Korrespondenzprinzip).<br />
Als Beispiel erwähnen wir den Drehimpulsoperator<br />
ˆ<br />
¯h<br />
l = r × ˆp = r × ∇. (63)<br />
i<br />
Den quantenmechanischen Operatoren ordnen wir Erwartungswerte<br />
6 <br />
V (u∆v − v∆u)d3r = <br />
∂V (u∇v − v∇u)d2S 7Man beachte, daß ∇ ohne den Vorfaktor i (vgl. (57)) diese Eigenschaft nicht besitzt!<br />
20
Ā = 〈 Â〉 =<br />
ψ ∗ Âψd 3 r (64)<br />
zu, die in gewisser Weise den Zahlwert <strong>der</strong> klassischen Variable A repräsentieren.<br />
Dieses allgemeine Konzept macht allerdings nur Sinn, wenn Ā immer reell ist.<br />
Und Operatoren, die diese Bedingung <strong>für</strong> alle Wellenfunktionen ψ erfüllen, heißen<br />
hermitesch. Diese Eigenschaft besitzen zwar alle reellen ˆ f = f(r) <strong>und</strong> ˆg = g(ˆp),<br />
aber lei<strong>der</strong> nicht beliebige Funktionen8 <strong>der</strong> Form (62). Ob das nach (61) gebildete<br />
 hermitesch wird, kann darüber hinaus von <strong>der</strong> Koordinatenwahl abhängen.<br />
Hier liegt <strong>der</strong> tiefere Gr<strong>und</strong> da<strong>für</strong>, daß wir beim Übergang zur Quantemechanik<br />
im allgemeinen keinen Gebrauch von generalisierte Koordinaten machen.<br />
Wir schränken unser Konzept <strong>der</strong> Operatoren also wie folgt ein: Ausgehend von<br />
dynamischen Variablen A(r, p) o<strong>der</strong> Observablen <strong>der</strong> klassischen Mechanik bilden<br />
wir korrespondierende quantenmechanische Operatoren  nach Gl.(62), sofern<br />
diese Operatoren zu reellen Erwartungswerten (64) führen (also sofern die<br />
Operatoren hermitesch sind). Das ist insbeson<strong>der</strong>e <strong>für</strong><br />
– alle reellen Funktionen f(r)<br />
– alle reellen Funktionen g(ˆp)<br />
– den Hamiltonoperator H = ˆp 2 /2m + V (r) (vgl. (61)) <strong>und</strong><br />
– den Drehimpulsoperator ˆ l = r × ˆp (vgl. (63)) erfüllt.<br />
Nachdem wir hiermit gr<strong>und</strong>sätzlich (<strong>und</strong> vorläufig) erklärt haben, was wir unter<br />
Operatoren <strong>und</strong> ihren Erwartungswerten verstehen, werden wir im folgenden auch<br />
die Kennzeichnung von Operatoren durch das Dach ˆ weglassen <strong>und</strong> beispielsweise<br />
unter p = −i¯h∇ einen Operator <strong>und</strong> unter ¯p = 〈p〉 seinen Erwartungswert<br />
verstehen.<br />
Um die Anschrift noch bequemer zu gestalten, führen wir die abkürzende Schreibweise<br />
ein. Offenbar gilt dann<br />
<br />
ϕ ∗ (r, t)χ(r, t)d 3 r = 〈ϕ|χ〉 (65)<br />
〈χ|ϕ〉 = 〈ϕ|χ〉 ∗ . (66)<br />
8 Es gilt beispielsweise <strong>für</strong> das äußere Produkt (63), nicht aber <strong>für</strong> das innere Produkt<br />
r · p. Das innere Produkt hermitescher Operatoren ist nur hermitesch, wenn die Operatoren<br />
vertauschbar sind.<br />
21
Die Schreibweise soll einmal an die Verwendung von eckigen Klammern zur Kennzeichnung<br />
von Mittelwerten erinnern. Gleichzeitig aber lehnt sie sich an die (veraltete)<br />
Schreibweise (a, b) <strong>für</strong> das innere Produkt a · b von Vektoren an. Die<br />
(quadratintegrablen) Funktionen |ϕ〉 = ϕ(r, t) spannen nämlich in <strong>der</strong> Tat einen<br />
linearen Raum H, den Hilbertraum, auf, in dem durch (65) ein Skalarprodukt<br />
definiert werden kann. Die Dimension von H ist abzählbar unendlich.<br />
Die Schreibweise (65) geht auf Dirac zurück. Er prägte – ausgehend von einer<br />
Aufspaltung des Wortes “bracket” – auch die Bezeichnungen bra–Vektor <strong>für</strong> 〈ϕ|<br />
<strong>und</strong> ket–Vektor <strong>für</strong> |χ〉. Damit unterscheidet er den Hilbertraum H von seinem<br />
Dualraum H + , <strong>der</strong> von den bra–Vektoren aufgespannt wird.<br />
Mit <strong>der</strong> neuen Schreibweise erhalten Erwartungswerte die suggestive Form<br />
〈A〉 = 〈ψ|A|ψ〉 o<strong>der</strong> 〈ψ|Aψ〉 (67)<br />
Repräsentiert A eine physikalische Observable, so muß 〈A〉 immer reell o<strong>der</strong> A<br />
hermitesch sein. Setzt man ψ = χ + λϕ, so folgt aus (67)<br />
〈A〉 = 〈χ|A|χ〉 + λ〈χ|Aϕ〉 + λ ∗ 〈ϕ|Aχ〉 + |λ| 2 〈ϕ|A|ϕ〉<br />
Ist A hermitesch, so sind die linke Seite sowie <strong>der</strong> erste <strong>und</strong> letzte Term <strong>der</strong><br />
rechten Seite reell. Also muß auch<br />
λ〈χ|Aϕ〉 + λ ∗ 〈ϕ|Aχ〉 = λ〈χ|Aϕ〉 + λ ∗ 〈Aχ|ϕ〉 ∗<br />
reell sein. Das kann aber nur <strong>für</strong> beliebige λ stimmen, wenn<br />
〈χ|Aϕ〉 = 〈Aχ|ϕ〉 (68)<br />
gilt. Umgekehrt garantiert (68) wegen (66) auch sofort reelle Erwartungswerte.<br />
Es ist daher üblich, hermitesche Operatoren durch die Beziehung (68) zu definieren.<br />
Wir erwähnen dies nicht allein <strong>der</strong> Vollständigkeit halber, son<strong>der</strong>n weil wir<br />
gelegentlich von <strong>der</strong> bequemen “Schieberegel” (68) <strong>für</strong> hermitesche Operatoren<br />
Gebrauch machen möchten.<br />
2.5 Das Theorem von Ehrenfest<br />
Wir fragen nach <strong>der</strong> Bewegung des Schwerpunkts eines Wellenpaketes (Vorsicht!)<br />
o<strong>der</strong> präziser nach <strong>der</strong> zeitlichen Entwicklung des Erwartungwertes ¯r(t) bzw.<br />
seiner x–Komponente<br />
22
¯x = 〈ψ|x|ψ〉 =<br />
ψ ∗ xψd 3 r<br />
Unter Benutzung <strong>der</strong> Schrödingergleichung erhalten wir<br />
= −¯h<br />
<br />
2im<br />
d¯x<br />
dt =<br />
<br />
ψ ∗ x ∂ψ ∂ψ∗<br />
+<br />
∂t ∂t xψ<br />
<br />
d 3 r = 1 −¯h<br />
i¯h<br />
2 <br />
2m<br />
(ψ ∗ x∆ψ − ∆ψ ∗ xψ) d 3 r<br />
∇ · {ψ ∗ x∇ψ − ∇ψ ∗ xψ}d 3 r + ¯h<br />
<br />
{∇(ψ<br />
2im<br />
∗ x) · ∇ψ − ∇ψ ∗ · ∇(xψ)}d 3 r<br />
Das erste Integral verschwindet nach dem Gaußschen Satz, im zweiten Integral<br />
differenzieren wir die Klammern ( ) aus. Mit (58)–(60) folgt dann<br />
d¯x<br />
dt<br />
¯h<br />
=<br />
2im ex<br />
<br />
· (ψ ∗ ∇ψ − ψ∇ψ ∗ )d 3 r<br />
= 1<br />
2m ex · (¯p + ¯p ∗ ) = 1<br />
m ex · ¯p = ¯px<br />
m .<br />
Eine entsprechende Beziehung erhält man natürlich auch <strong>für</strong> die übrigen Komponenten,<br />
es gilt also<br />
d 1<br />
〈r〉 = 〈p〉. (69)<br />
dt m<br />
Diese “klassische” Beziehung zwischen den Erwartungswerten r <strong>und</strong> p bestätigt<br />
eindrucksvoll das Konzept des Impulsoperators aus dem vorigen Abschnitt. Die<br />
entsprechende Beziehung <strong>für</strong> d¯p/dt, die wir nun schon ahnen, ergibt sich fast noch<br />
einfacher: Aus [vgl. (58)]<br />
¯px = 〈ψ|px|ψ〉 = ¯h<br />
<br />
i<br />
∗ ∂ψ<br />
ψ<br />
∂x d3r berechnen wir mit <strong>der</strong> Schrödingergleichung [vgl. (42) <strong>und</strong> (43)]<br />
d¯px<br />
dt<br />
= ¯h<br />
<br />
1<br />
−<br />
i i¯h<br />
¯h2<br />
<br />
2m<br />
<br />
ψ ∗ ∆ ∂ψ<br />
∂x<br />
<br />
¯h<br />
=<br />
i<br />
<br />
<br />
∗ ∂ ∂ψ ∂ψ∗ ∂ψ<br />
ψ + d<br />
∂x ∂t ∂t ∂x<br />
3 r<br />
<br />
∂ψ<br />
− ∆ψ∗ d<br />
∂x<br />
3 <br />
r +<br />
<br />
∗ ∂<br />
ψ<br />
∂x V ψ − ψ∗V ∂ψ<br />
<br />
d<br />
∂x<br />
3 <br />
r .<br />
23
Das erste Integral verschwindet nach dem Greenschen Satz [vgl. die ähnliche<br />
Rechnung vor (61)], im zweiten differenzieren wir aus <strong>und</strong> erhalten<br />
d¯px<br />
dt<br />
1<br />
=<br />
i2 <br />
∗ ∂V<br />
ψ<br />
∂x ψd3r = − ∂V<br />
∂x<br />
o<strong>der</strong> verallgemeinert auf alle Impulskomponenten<br />
Damit lassen sich die klassischen Beziehungen<br />
d<br />
〈p〉 = −〈∇V (r)〉. (70)<br />
dt<br />
˙r = p/m <strong>und</strong> ˙p = −∇V<br />
<strong>für</strong> ein Teilchen im konservativem Kraftfeld also in eindrucksvoll enger Analogie<br />
auf die quantenmechanischen Erwartungswerte übertragen. Diese Form <strong>der</strong> Korrespondenz<br />
zwischen klassischer– <strong>und</strong> <strong>Quantenmechanik</strong> wird als Theorem von<br />
Ehrenfest (1927) bezeichnet.<br />
Trotz <strong>der</strong> engen Analogie besteht ein wichtiger Unterschied zur klassischen Bewegungsgleichung<br />
eines Teilchens. Wenn wir nämlich versuchsweise 〈r〉 mit dem<br />
Teilchenort r identifizieren, erhalten wir klassisch<br />
m〈¨r〉 = −∇V (〈r〉).<br />
Dies ist aber im allgemeinem verschieden von <strong>der</strong> quantenmechanischen Beziehung<br />
m〈¨r〉 = −〈∇V (r)〉, (71)<br />
die aus (69) <strong>und</strong> (70) folgt. Im Gegensatz zum klassischen Teilchen tastet das<br />
“quantenmechanische Teilchen” also das Potential <strong>der</strong> gesamten Nachbarschaft<br />
ab (Feynman).<br />
Auf <strong>der</strong> an<strong>der</strong>en Seite ist (71) aber identisch mit <strong>der</strong> Newtonschen Bewegungsgleichung<br />
<strong>für</strong> den Schwerpunkt eines klassischen Viel–Teilchen–Systems, wenn man<br />
unter 〈 〉 die gewichtete Summation über alle Massenpunkte versteht. Hierdurch<br />
erhält das anschauliche Bild einer ausgeschmierten Wolke <strong>der</strong> Dichte ψ ∗ ψ, die<br />
ein “quantenmechanisches Teilchen” repräsentiert, eine wesentliche Stütze. (Wir<br />
halten trotzdem an <strong>der</strong> Ablehnung dieses Bildes fest, da es in an<strong>der</strong>en Punkten<br />
völlig versagt!)<br />
24
Abschließend sei darauf hingewiesen, daß — abgesehen von einfachen Spezialfällen<br />
— auch in <strong>der</strong> klassischen Mechanik <strong>der</strong> Schwerpunktsatz nicht ausreicht, um die<br />
Bewegung des Schwerpunkts eines Systems zu berechnen.<br />
2.6 Die Heisenbergsche Unschärferelation<br />
Wir haben bereits mehrfach erwähnt, daß die <strong>Quantenmechanik</strong> es prinzipiell<br />
nicht erlaubt, die nötigen Anfangsbedingungen <strong>für</strong> eine klassische Beschreibung<br />
präzise anzugeben. Dies folgt mathematisch aus <strong>der</strong> berühmten Unschärferelation,<br />
die wir nun herleiten <strong>und</strong> diskutieren wollen.<br />
Wir beginnen mit einer “elementaren” Herleitung <strong>für</strong> ein eindimensionales Wellenpaket<br />
ψ(x). In Anlehnung an das klassische Lehrbuch von Messiah 9 bilden wir<br />
<strong>für</strong> λ ∈ R die Hilfsfunktion<br />
<strong>und</strong> rechnen<br />
<br />
I(λ) =<br />
x 2 ψ ∗ <br />
ψdx + λ<br />
<br />
I(λ) =<br />
<br />
<br />
xψ + λ ∂ψ<br />
<br />
<br />
<br />
<br />
∂x <br />
x<br />
2<br />
dx ≥ 0 (72)<br />
<br />
<br />
∗ ∂ψ ∂ψ∗<br />
ψ + ψ dx + λ<br />
∂x ∂x<br />
2<br />
∗ ∂ψ ∂ψ<br />
∂x ∂x dx.<br />
Wenn wir (. . .) = ∂[ψ ∗ ψ]/∂x beachten <strong>und</strong> die beiden letzten Integrale partiell<br />
integrieren, folgt<br />
I(λ) =<br />
<br />
ψ ∗ x 2 <br />
ψdx − λ<br />
wobei wir den Operator<br />
ψ ∗ ψdx − λ 2<br />
<br />
k = 1<br />
i<br />
∂<br />
∂x<br />
∗ ∂2<br />
ψ<br />
∂x2 ψdx = 〈x2 〉 − λ + λ 2 〈k 2 〉,<br />
(73)<br />
eingeführt haben. I(λ) beschreibt eine nach oben geöffnete Parabel, I(λ) ≥ 0<br />
muß insbeson<strong>der</strong>e <strong>für</strong> den Scheitelpunkt λs gelten. Aus dI/dλ = 0 erhalten wir<br />
also<br />
λs = 1<br />
2〈k 2 〉<br />
<strong>und</strong> I(λs) = 〈x 2 〉 − 1<br />
2〈k2 1<br />
+<br />
〉 4〈k2 ≥ 0 ,<br />
〉<br />
9 A. Messiah, <strong>Quantenmechanik</strong>, Bd. I, Abschnitt 4.2.2<br />
25
〈x 2 〉〈k 2 〉 ≥ 1<br />
. (74)<br />
4<br />
Damit haben wir die Beziehung (17), die wir an einem Beispiel abgelesen haben,<br />
verallgemeinert <strong>und</strong> präzisiert 10 . Das Gleichheitszeichen gilt genau dann, wenn<br />
<strong>der</strong> Integrand in Gl. (72) identisch verschwindet, also <strong>für</strong> Gaußsche Wellenfunktionen<br />
Mit px = ¯hk geht (74) in<br />
ψ ∼ exp −x2<br />
2λ .<br />
〈x 2 〉〈p 2 ¯h2<br />
x 〉 ≥<br />
4<br />
über. Ein Teilchen kann also nicht exakt am Ort x = 0 ruhen (px = 0). Dieser<br />
Wi<strong>der</strong>spruch ergibt sich aber auch <strong>für</strong> jede an<strong>der</strong>e exakt formulierte Anfangsbedingung,<br />
denn wir brauchen ja nur x durch ∆x = x − x0 <strong>und</strong> p durch ∆p = p − p0<br />
zu ersetzen (Wechsel des Bezugssystems). So erhalten wir endlich die Heisenbergsche<br />
Unschärferelation<br />
〈∆x 2 〉〈∆p 2 ¯h2<br />
x 〉 ≥ . (75)<br />
4<br />
Bevor wir die Unschärferelation weiter diskutieren, wollen wir unsere Herleitung<br />
auf beliebige Observable A <strong>und</strong> B verallgemeinern. Das wird uns zugleich einen<br />
völlig neuen Geschichtspunkt liefern. In Anlehnung an Gl. (72) bilden wir dazu<br />
die Hilfsfunktion<br />
<br />
I(λ) = |Aψ − iλBψ| 2 dτ ≥ 0, (76)<br />
wobei A <strong>und</strong> B hermitesche Operatoren repräsentiern <strong>und</strong> dτ <strong>für</strong> dx o<strong>der</strong> d 3 r<br />
steht. Wenn wir nun dem Rechengang auf <strong>der</strong> vorigen Seite folgen, haben wir<br />
lediglich zu beachten, daß wir die partiellen Integrationen in die Verschiebung<br />
hermitescher Operatoren übersetzen müssen. Damit erhalten wir<br />
ten.<br />
<br />
I(λ) =<br />
ψ ∗ (A + iλB)(A − iλB)ψdτ = 〈A 2 〉 + λ 2 〈B 2 〉 − iλ〈(AB − BA)〉 .<br />
10 Der Faktor 1/4 gegenüber Gl.(17) kommt daher, daß wir mit ψ ∗ ψ <strong>und</strong> nicht mit ψ gewich-<br />
26
Wir bestimmen wie<strong>der</strong> den Scheitelpunkt<br />
λs = i<br />
<strong>der</strong> Parabel I(λ) <strong>und</strong> folgern aus I(λs) ≥ 0<br />
〈A 2 〉〈B 2 〉 ≥<br />
〈AB − BA〉<br />
〈B 2 〉<br />
AB − BA<br />
Hiermit ist die formale Rechnung schon abgeschlossen. Wie oben können wir A<br />
durch ∆A = A − Ā <strong>und</strong> B durch ∆B = B − ¯ B ersetzen <strong>und</strong> erhalten mit dem<br />
Kommutator<br />
die allgemeine Unschärferelation<br />
2i<br />
2<br />
.<br />
[A, B] = AB − BA (77)<br />
〈(∆A) 2 〉〈(∆B) 2 〉 ≥<br />
[A, B]<br />
2i<br />
2<br />
. (78)<br />
Sie sagt also beispielsweise aus, daß zwischen x <strong>und</strong> px deshalb eine Unschärferelation<br />
besteht, weil x <strong>und</strong> px nicht vertauschbar sind. Es gilt nämlich<br />
∂<br />
(xψ) − x∂ψ<br />
∂x ∂x<br />
<br />
∂<br />
, x =<br />
∂x ∂ ∂<br />
x − x<br />
∂x ∂x<br />
= ψ o<strong>der</strong><br />
[px, x] = pxx − xpx = ¯h<br />
i<br />
= 1 also<br />
. (79)<br />
Neben dieser neuen Interpretation haben wir damit eine wesentliche Verallgemeinerung<br />
<strong>der</strong> Unschärferelation erhalten: Eine Unschärferelation besteht zwischen<br />
allen Observablen, <strong>der</strong>en Operatoren nicht vertauschbar sind, <strong>und</strong> Gl. (78) sagt<br />
uns, wie die Unschärferelation in jedem Fall genau aussieht.<br />
Ein wichtiges Beispiel hierzu ist die Unschärferelation zwischen den verschiedenen<br />
Komponenten des Drehimpulses (vgl. (63)) l = r × p. Mit<br />
lx = ypz − zpy <strong>und</strong><br />
27
folgt nämlich<br />
Wegen<br />
ly = zpx − xpz<br />
[lx, ly] = lxly − lylx<br />
= (ypz − zpy)(zpx − xpz) − (zpx − xpz)(ypz − zpy)<br />
= ypx[pz, z] + xpy[z, pz] = − (xpy − ypx)[pz, z].<br />
lz = xpy − ypx <strong>und</strong> [pz, z] = −i¯h<br />
[vgl. (79)] folgt daraus die wichtige Vertauschungsrelation<br />
[lx, ly] = i¯hlz<br />
(80)<br />
<strong>und</strong> natürlich die entsprechenden durch zyklische Vertauschung gewonnenen Relationen.<br />
Gemäß Gl.(78) bedeutet das aber, daß die drei Komponenten des Drehimpulses<br />
nicht präzise angegeben werden können, denn es besteht die Unschärferelation<br />
〈∆l 2 x 〉〈∆l2 ¯h2<br />
y 〉 ≥<br />
4 〈lz〉 2 , (81)<br />
o<strong>der</strong> — wie wir etwas weniger präzise schreiben können —<br />
δlx · δly ≥ ¯h<br />
2 |〈lz〉|. (82)<br />
Wir führen die “unscharfen Werte” eines Observablenpaares also darauf zurück,<br />
daß ihre Operatoren “nicht vertauschbar” sind. Das typische Beispiel – <strong>und</strong> den<br />
Ausgangspunkt aller weiterer Rechnungen – liefern die Operatoren x <strong>und</strong> ∂/∂x<br />
mit dem Kommutator<br />
<br />
∂<br />
, x = 1.<br />
∂x<br />
Die entsprechende Unschärfe können wir uns direkt an <strong>der</strong> Wahrscheinlichkeitsdichte<br />
p(x) veranschaulichen: Eine gut lokalisierbare Verteilung (Skizza a) entspricht<br />
einem steilen Peak mit großen Gradienten ∂/∂x, während eine flache Verteilung<br />
mit kleinen Gradienten (Skizze b) den Ort nur sehr ungenau festlegt:<br />
28
p(x)<br />
δx<br />
a)<br />
x<br />
p(x)<br />
Die Orts–Impuls–Unschärfe ist also die natürlichste Sache <strong>der</strong> Welt, wenn man<br />
akzeptiert, daß <strong>der</strong> Impuls durch den Gradienten repräsentiert wird. Das aber<br />
entspricht gerade <strong>der</strong> Wellenbeschreibung, die uns von den Interferenzbeobachtungen<br />
aufgedrängt wurde. Die Rückführung <strong>der</strong> Unschärferelation auf die Nicht–<br />
Vertauschbarkeit von Operatoren ist damit nur eine abstrakte Formulierung <strong>der</strong><br />
Unvereinbarkeit von Begriffen, die dem Teilchenbild (Ort) <strong>und</strong> dem Wellenbild<br />
(Wellenzahl) entlehnt sind.<br />
Für die physikalische Interpretation ist ein Gedankenexperiment wichtig, das Heisenberg<br />
(mit Hilfestellung Bohrs) 1927 angegeben hat: Wir wollen die Ortsbestimmung<br />
eines Teilchens (z. B. Elektrons) konkret mit einem Mikroskop durchführen.<br />
Dann erhalten wir eine minimale Ortsunschärfe<br />
δx ∼ λ<br />
sin ε ,<br />
die dem Auflösungsvermögen des Mikroskops entspricht. Dabei ist λ die Wellenlänge<br />
des verwendeten Lichts <strong>und</strong> sin ε die numerische Apertur (d. h. <strong>der</strong> Sinus<br />
des halben Öffnungswinkels). Nun besteht aber das Licht aus Photonen mit<br />
einem Impuls<br />
p = ¯hk = h/λ.<br />
Wenn ein Photon von Teilchen gestreut wird — <strong>und</strong> nur dadurch entsteht ja das<br />
29<br />
ε<br />
δx<br />
b)<br />
x
Bild im Mikroskop — überträgt es einen Teil seines Impulses (Compton–Effekt).<br />
Aufgr<strong>und</strong> <strong>der</strong> Streuung erhält das Teilchen nun eine Impulsunschärfe<br />
δpx ∼ p sin ε = h<br />
sin ε.<br />
λ<br />
Unsere Kenntnis über das Teilchen ist also durch ein minimales Unschärfeprodukt<br />
eingeschränkt.<br />
δx · δpx ∼ h<br />
Mit diesem Gedankenexperiment lieferte <strong>der</strong> Positivist Heisenberg im Gr<strong>und</strong>e<br />
seinen dem Realismus verschworenen Gegnern hervorragende Munition: Ist es<br />
nicht doch so, daß das Teilchen “eigentlich” einen scharfen Ort <strong>und</strong> scharfen<br />
Impuls hat, <strong>und</strong> daß die Unschärfe “nur” auf <strong>der</strong> Störung durch die Beobachtung<br />
beruht?<br />
Diese “Störung” läßt sich allerdings nicht durch eine Re–Interpretation <strong>der</strong> Meßresultate<br />
“wegrechnen”: δpx ist eine wirkliche “Unschärfe”, <strong>der</strong> übertragene Impuls<br />
läßt sich nicht angeben, da die Abbildung im Mikroskop tatsächlich ein<br />
divergentes Lichtbündel voraussetzt (worauf Bohr hingewiesen hat). Und da <strong>der</strong><br />
Impulsübertrag prinzipiell nicht berechenbar ist, ist es <strong>für</strong> den Physiker wie<strong>der</strong><br />
prinzipiell unentscheidbar, ob die Positivisten o<strong>der</strong> die Realisten recht haben: Wir<br />
können nur unsere Beobachtung beschreiben.<br />
Mir scheint noch ein an<strong>der</strong>er Aspekt <strong>der</strong> mikroskopischen Ortsbestimmung wichtig:<br />
Wir hatten die Unschärferelation in den bisherigen Diskussionen auf den<br />
Welle–Teilchen–Dualismus zurückgeführt. In Heisenbergs Gedankenexperiment<br />
spielt <strong>der</strong> Wellenaspekt des beobachteten Teilchens jedoch nirgendwo eine Rolle.<br />
Der Welle–Teilchen–Dualismus wird hier auf das Photon verlagert (Auflösungsvermögen<br />
<strong>und</strong> Wellenlänge einerseits, Comptoneffekt an<strong>der</strong>seits). Darin liegt<br />
erneut eine Bestätigung <strong>der</strong> Aussage, daß die Quantemechanik nicht ein Teilchen<br />
an sich son<strong>der</strong>n die prinzipielle Möglichkeit seiner Beobachtung beschreibt.<br />
Später (im Abschnitt 5.6) werden wir sogar sehen, daß die Unschärfe auch bei<br />
einer völlig störungsfreien Messung unvermeidlich ist.<br />
Wenn wir noch einmal auf die Begründung <strong>der</strong> Unschärfe durch den Welle–<br />
Teilchen–Dualismus zurückkommen, so gilt in völliger Analogie zur Unschärfe<br />
δx·δk ≥ 1/2 eine Unschärfe δt·δω ≥ 1/2. Mit ¯hω = E folgt daraus die Energie–<br />
Zeit–Unschärfe<br />
δE · δt ≥ ¯h<br />
. (83)<br />
2<br />
30
Wir wollen uns das direkt an <strong>der</strong> Wellenfunktion veranschaulichen: Ist die Energie<br />
E <strong>und</strong> damit ω = E/¯h präzise vorgegeben, haben wir eine Wellenfunktion<br />
ψ(r, t) = ϕ(r)e −iωt .<br />
Ihre ”Zeitabhängigkeit” e −iωt ist nicht beobachtbar, denn die Aufenthaltswahrscheinlichkeit<br />
ψ ∗ (r, t)ψ(r, t) = |ϕ(r)| 2<br />
hängt gar nicht von <strong>der</strong> Zeit ab. Die Wellenfunktion, die <strong>der</strong> präzisen Vorgabe<br />
<strong>der</strong> Energie (δE = 0) entspricht, beschreibt also einen stationären Zustand, <strong>der</strong><br />
unendlich lange dauert (δt = ∞).<br />
Zur Zeitabhängigkeit eines Zustandes mit unscharfer Energie betrachten wir eine<br />
Wellenfunktion<br />
ψ(r, t) = ϕ1(r)e −iω1t + ϕ2(r)e −iω2t<br />
<strong>und</strong> rechnen<br />
ψ ∗ ψ = |ϕ1| 2 + |ϕ2| 2 + 2Re <br />
ϕ ∗ <br />
i(ω1−ω2)t<br />
1ϕ2e<br />
Der letzte Term zeigt also eine zeitliche Schwebung mit <strong>der</strong> Periodendauer<br />
τ =<br />
2π<br />
|ω1 − ω2| =<br />
h<br />
|E1 − E2| .<br />
Um die Energiedifferenz ∆E = |E1 − E2| aufzulösen (d. h. um die Schwebung zu<br />
beobchten), muß man also die Messung mindestens über Zeiten ∆t ∼ τ = h/∆E<br />
ausdehnen.<br />
Alternativ können wir die Energie–Zeit–Unschärfe erhalten, indem wir die Ortsunschärfe<br />
mit Hilfe <strong>der</strong> Geschwindigkeit auf den Zeitpunkt <strong>der</strong> Beobachtungung<br />
übertragen: Wir fragen etwa, wann ein Teilchen die Marke x = x0 passiert <strong>und</strong><br />
schätzen ab<br />
δt = δx<br />
v<br />
m<br />
= δx =⇒<br />
p<br />
δt p<br />
¯h<br />
δp = δxδp ≥<br />
m 2 .<br />
Mit pδp/m = δ(p 2 /2m) = δE folgt daraus (83).<br />
31
Wenn diese Diskussion auch die völlige Analogie <strong>der</strong> Energie–Zeit– <strong>und</strong> Orts–<br />
Impuls–Unschärferelation deutlich gemacht hat, so kommt diesen Relationen doch<br />
eine ganz unterschiedliche Rolle im Rahmen <strong>der</strong> formalen Theorie zu:<br />
Ort x <strong>und</strong> Impuls p sind (gleichberechtigte 11 ) Observable, die in <strong>der</strong> Theorie durch<br />
Operatoren repräsentiert werden. Die Unschärfe beruht darauf, daß <strong>der</strong> Orts– <strong>und</strong><br />
<strong>der</strong> Impulsoperator nicht vertauschbar sind.<br />
Dagegen wird die Zeit t in <strong>der</strong> <strong>Quantenmechanik</strong> nicht durch einen Operator<br />
repräsentiert son<strong>der</strong>n spielt die Rolle eines Parameters. Diese Unsymmetrie, die<br />
auch vom Gesichtspunkt <strong>der</strong> Relativität als Defizit erscheint, hat Schrödinger bei<br />
<strong>der</strong> Aufstellung <strong>der</strong> Wellengleichung vergeblich zu vermeiden versucht.<br />
11 Auch das “Ungleichgewicht” p ∼ d/dx läßt sich durch einen Wechsel <strong>der</strong> “Darstellung”<br />
beseitigen: In <strong>der</strong> “Impulsdarstellung” (Fouriertransformation) gilt x ∼ d/dp.<br />
32
3 Spezielle Lösungen <strong>der</strong> Schrödingergleichung<br />
Die Schrödingergleichung ist eine partielle Differentialgleichung, die nicht allgemein<br />
in geschlossener Form gelöst werden kann. Wenn wir uns in diesem Kapitel<br />
mit ihrer Lösung <strong>für</strong> einige ausgewählte Probleme befassen, so wollen wir damit<br />
in erster Linie generelle Zusammenhänge aufzeigen o<strong>der</strong> verdeutlichen. Gleichzeitig<br />
lernen wir so einige Lösungsmethoden <strong>und</strong> wichtige “Schulbeispiele” kennen,<br />
ohne dabei jedoch “Vollständigkeit” anzustreben.<br />
3.1 Entwicklung nach Eigenfunktionen des Hamiltonoperators<br />
Wir setzen voraus, daß die Hamiltonfunktion nicht explizit von <strong>der</strong> Zeit abhängt,<br />
so daß klassisch <strong>der</strong> Energiesatz H(x, p) = E gilt. Dann können wir nach partikulären<br />
Lösungen <strong>der</strong> Schrödingergleichung fragen, die dem Separationsansatz<br />
genügen. Mit<br />
folgt<br />
o<strong>der</strong><br />
i¯h ∂ψ<br />
∂t<br />
ψ(r, t) = g(t)ϕ(r) (84)<br />
¯h2<br />
= Hψ = − ∆ψ + V (r)ψ<br />
2m<br />
i¯hϕ(r) dg<br />
dt<br />
i¯h dg<br />
g dt<br />
= g(t)Hϕ(r)<br />
= 1<br />
ϕ Hϕ.<br />
Nun hängt die linke Seite nur von t, die rechte nur von r ab. Also sind beide gleich<br />
einer Konstanten Eν. Dabei soll <strong>der</strong> Index ν andeuten, daß wir im allgemeinen nur<br />
<strong>für</strong> bestimmte Werte von E sinnvolle Lösungen finden werden. Die Abhängigkeit<br />
<strong>der</strong> Lösung von dieser Konstanten kennzeichnen wir ebenfalls durch den Index ν<br />
<strong>und</strong> erhalten dgν/dt = −iEν/¯hgν o<strong>der</strong><br />
Eν<br />
−i<br />
gν(t) = e ¯h t . (85)<br />
33
gν ist also — wie nicht an<strong>der</strong>s zu erwarten — <strong>der</strong> zeitabhängige Phasenfaktor,<br />
<strong>der</strong> im Wellenbild die vorgegebene Energie Eν repräsentiert. Die zugehörige Ortsfunktion<br />
ϕν(r) ist Lösung <strong>der</strong> stationären Schrödingergleichung<br />
<br />
− ¯h2<br />
<br />
∆ + V (r)<br />
2m<br />
ϕν(r) = Eνϕν(r)<br />
o<strong>der</strong> H|ϕν〉 = Eν|ϕν〉. (86)<br />
Gl. (86) ist vom Typ eines Eigenwertproblems, wir nennen Eν einen Eigenwert <strong>und</strong><br />
ϕν(r) eine Eigenfunktion (bzw. |ϕν〉 einen Eigenvektor) des Hamiltonoperators.<br />
Im Hinblick auf eine mögliche Entwicklung <strong>der</strong> allgemeinen Lösung nach solchen<br />
Eigenfunktionen wollen wir zeigen, daß die Eigenfunktionen zu verschiedenen<br />
Eigenwerten orthogonal sind. Dazu gehen wir von <strong>der</strong> Schrödingergleichung<br />
¯h<br />
∆ϕ = [V (r) − E]ϕ<br />
2m<br />
aus <strong>und</strong> bilden 12 unter Verwendung des Greenschen Satzes [vgl. die Rechnung zu<br />
Gl. (61)]<br />
also<br />
0 = ¯h2<br />
<br />
(ϕν∆ϕµ − ϕµ∆ϕν)d<br />
2m<br />
3 r<br />
<br />
= (ϕνV ϕµ − ϕµV ϕν)d 3 <br />
r − ϕν(Eµ − Eν)ϕνd 3 <br />
r<br />
= (Eν − Eµ) ϕνϕµd 3 r = (Eν − Eµ)〈ϕν|ϕµ〉,<br />
〈ϕν|ϕµ〉 = 0 <strong>für</strong> Eν = Eµ. (87)<br />
Der Greensche Satz (die partielle Integration), auf dem unser Beweis beruht,<br />
drückt im Gr<strong>und</strong>e nur aus, daß <strong>der</strong> Hamiltonoperator hermitesch ist. Tatsächlich<br />
erhalten wir direkt aus <strong>der</strong> Eigenwertgleichung (86) eines beliebigen hermiteschen<br />
Operators H unter Ausnutzung <strong>der</strong> “Schieberegel” (68)<br />
0 = 〈Hϕν|ϕµ〉 − 〈ϕν|Hϕµ〉 = (E ∗ ν<br />
Diese kurze, elegante Rechnung zeigt<br />
− Eµ)〈ϕν|ϕµ〉.<br />
12 Im Gegensatz zur zeitabhängigen Schrödingergleichung ist die stationäre Schrödingergleichung<br />
nicht komplex <strong>und</strong> wir können reelle Eigenfunktionen wählen.<br />
34
1. <strong>für</strong> ν = µ, daß alle Eigenwerte hermitescher Operatoren reell sind <strong>und</strong><br />
2. <strong>für</strong> ν = µ, daß Eigenfunktionen zu verschiedenen Eigenwerten hermitescher<br />
Operatoren orthogonal sind.<br />
Die Entwicklung nach den Eigenfunktionen des Hamiltonoperators, die wir hier<br />
besprechen wollen, stellt tatsächlich nur einen Spezialfall <strong>der</strong> allgemeineren Entwicklung<br />
nach den Eigenfunktionen irgendeines hermiteschen Operators dar. Wir<br />
werden hierauf bei Bedarf zurückkommen, gehen aber nun nicht weiter darauf<br />
ein.<br />
Wegen <strong>der</strong> Linearität <strong>der</strong> Schrödingergleichung sind beliebige Linearkombinationen<br />
unserer partikulären Lösungen gν(t)ϕν(r) ebenfalls Lösungen. Wir können<br />
nun umgekehrt fragen, ob jede Lösung ψ(r, t) <strong>der</strong> Schrödingergleichung in <strong>der</strong><br />
Form<br />
ψ(r, t) = <br />
ν<br />
Eν<br />
−i<br />
cνe ¯h t ϕν(r) (88)<br />
nach den Eigenfunktionen ϕν(r) des Hamiltonoperators entwickelt werden kann.<br />
Dies ist die Frage nach <strong>der</strong> Vollständigkeit 13 des Funktionssystems {ϕν}. Die<br />
Vollständigkeit ist mathematisch meistens schwierig nachzuweisen, tatsächlich<br />
aber nur in “pathologischen” Fällen verletzt — vorausgesetzt, man hat tatsächlich<br />
alle Eigenwerte <strong>und</strong> die entsprechenden Eigenfunktionen gef<strong>und</strong>en. Wir werden<br />
daher die Vollständigkeit stets voraussetzen <strong>und</strong> davon ausgehen, daß die Entwicklung<br />
(88) immer möglich ist.<br />
Aus <strong>der</strong> Orthogonalität folgt darüber hinaus, daß die Entwicklung sogar eindeutig<br />
<strong>und</strong> sehr einfach zu berechnen ist. Wir können die Eigenfunktionen nämlich so<br />
normieren, daß<br />
〈ϕν|ϕµ〉 = δνµ<br />
gilt. Schreiben wir (88) nun in <strong>der</strong> Form<br />
|ψt=0〉 = <br />
cµ|ϕµ〉<br />
<strong>und</strong> multiplizieren mit 〈ϕν|, so folgt wegen (89)<br />
µ<br />
(89)<br />
13 Zur Veranschaulichung nicht vollständiger Systeme denke man an eine “Basis” aus m Vektoren<br />
im n-dimensionalen Vektorraum (m < n) o<strong>der</strong> an Potenzreihen, in denen bestimmte<br />
Potenzen nicht erlaubt sind.<br />
35
cν = 〈ϕν|ψt=0〉<br />
<br />
(90)<br />
= ϕ ∗ ν (r)ψ(r, 0)d3r. Wir wollen diesen formalen Abschnitt mit dem Hinweis auf zwei Schwierigkeiten<br />
abschließen:<br />
Wir haben bisher stillschweigend vorausgesetzt, daß die Eigenwerte Eν <strong>und</strong> Eµ<br />
<strong>für</strong> ν = µ tatsächlich verschieden sind, o<strong>der</strong> an<strong>der</strong>s ausgedrückt, daß zu einem Eigenwert<br />
nicht mehrere linear unabhängige Eigenfunktionen existieren. Wenn das<br />
nicht erfüllt ist, spricht man von Entartung: Der Eigenwert Eν heißt k–fach entartet,<br />
wenn k linear unabhängige Eigenfunktionen zu Eν existieren. Die formale<br />
Schwierigkeit <strong>der</strong> Entartung liegt darin, daß entartete Eigenfunktionen nicht mehr<br />
automatisch orthogonal untereinan<strong>der</strong> sind. Man kann jedoch stets orthogonale<br />
Eigenfunktionen finden <strong>und</strong> damit die Gültigkeit von (89) <strong>und</strong> (90) sicherstellen.<br />
Eine zweite stillschweigende Voraussetzung ging davon aus, daß wir nur diskrete<br />
Eigenwerte Eν haben. Auch das ist nicht immer erfüllt, im Gegenteil, das<br />
“Spektrum” möglicher Eigenwerte weist typischerweise einen diskreten <strong>und</strong> einen<br />
kontinuierlichen Anteil auf. Die entsprechende Interpretation von Gl. (88) liegt<br />
auf <strong>der</strong> Hand: Wir ersetzen die Summation im kontinuierlichen Anteil durch eine<br />
Integration:<br />
ψ(r, t) = <br />
Eν t<br />
−<br />
cνe ¯h ϕν(r)dν. (91)<br />
Was aber sollen wir in Gl. (89) unter dem Kroneckersymbol δνµ im kontinuierlichen<br />
Teil des Spektrums verstehen? Durch geeignete Grenzübergänge läßt sich<br />
erreichen, daß man die kontinuierlichen Eigenfunktionen durch<br />
〈ϕν|ϕµ〉 = δ(ν − µ) (92)<br />
“normieren” kann. Die Singularität <strong>der</strong> δ–Funktion <strong>für</strong> ν = µ deutet aber schon<br />
an, daß wir hier eigentlich vor einer ernsteren Schwierigkeit stehen: Unsere Eigenfunktionen<br />
sind nicht mehr im üblichen Sinn normierbar <strong>und</strong> wir verlassen den<br />
Hilbertraum.<br />
Wir werden diese Schwierigkeit nicht systematisch mit mathematischen Mitteln<br />
beheben. Wir werden aber notgedrungen bei kontinuierlichen Spektren mit ihr<br />
konfrontiert <strong>und</strong> werden sie dort intuitiv durch die physikalische Interpretation<br />
entschärfen.<br />
36
3.2 Der harmonische Oszillator<br />
Wir beginnen mit einem einfachen, wegen seiner gr<strong>und</strong>legenden Bedeutung <strong>für</strong><br />
zahlreiche physikalische Modelle aber beson<strong>der</strong>s wichtigen Schulbeispiel <strong>und</strong> untersuchen<br />
den eindimensionalen harmonischen Oszillator mit <strong>der</strong> Hamiltonfunktion<br />
H = p2 kF<br />
+<br />
2m 2 x2 = p2 mω2<br />
+<br />
2m 2 x2 , (93)<br />
wobei kF die Fe<strong>der</strong>konstante <strong>und</strong> ω = (kF /m) 1/2 die klassische Frequenz bezeichnet.<br />
Die stationäre Schrödingergleichung Hϕ = Eϕ lautet dann<br />
− ¯h2 d<br />
2m<br />
2 <br />
2 ϕ mω<br />
+<br />
dx2 2 x2 <br />
− E ϕ = 0. (94)<br />
Die lästigen Vorfaktoren können wir durch eine Transformation<br />
auf eine dimensionslose Ortskoordinate ξ wegschaffen:<br />
Wählen wir nun<br />
so folgt<br />
¯h 2<br />
2mx 2 0<br />
¯h 2<br />
mx 2 0<br />
¯hω<br />
2<br />
Gehen wir schließlich noch durch<br />
x = x0ξ (95)<br />
d2ϕ dξ2 + Eϕ − mω2x2 0<br />
ξ<br />
2<br />
2 ϕ = 0.<br />
= mω 2 x 2 0 o<strong>der</strong> x 2 0<br />
d2 <br />
ϕ<br />
+ E −<br />
dξ2 ¯hω<br />
2 ξ2<br />
<br />
ϕ = 0.<br />
E = λ ¯hω<br />
2<br />
¯h<br />
= , (96)<br />
mω<br />
zu einem dimensionslosen Energiewert λ über, so erhält die Schrödingergleichung<br />
des harmonischen Oszillators die übersichtliche Gestalt<br />
37<br />
(97)
hϕ =<br />
<br />
ξ 2 − d2<br />
dξ2 <br />
ϕ = λϕ. (98)<br />
Bevor wir dieses Eigenwertproblem explizit lösen, merken wir an, daß alle Eigenwerte<br />
positiv sind. Für λ ≤ 0 wäre nämlich ϕ ′′ immer ≥ 0, ϕ also konvex zur<br />
x–Achse:<br />
ϕ<br />
ξ<br />
ϕ<br />
Eine solche Wellenfunktion ist aber sicher nicht normierbar. Der formale Beweis<br />
folgt aus <strong>der</strong> kleinen Rechnung<br />
<br />
(λ − ξ 2 )ϕ 2 <br />
dξ = −<br />
ξ<br />
ϕϕ ′′ <br />
dξ = +<br />
ϕ ′2 dξ > 0,<br />
die zeigt, daß <strong>der</strong> Integrand links nicht negativ definit sein kann.<br />
Daß negative λ ausgeschlossen sind, entspricht auch unserer klassischen Erwartung.<br />
Denn E = p 2 /2m+kx 2 /2 ist nach Konstruktion immer ≥ 0. Darüber hinaus<br />
verbietet die <strong>Quantenmechanik</strong> aber auch E = 0 (warum?).<br />
Für λ > 0 erhalten wir ein Intervall ξ 2 < λ, in dem ϕ(ξ) konkav zur Achse<br />
ist. Damit können wir uns normierbare Wellenfunktionen <strong>für</strong> bestimmte Werte<br />
von λ vorstellen. Dies wird durch die numerischen Ergebnisse auf <strong>der</strong> folgenden<br />
Seite bestätigt: Integrieren wir Gl. (98) <strong>für</strong> wachsende λ > 0, so erhalten wir <strong>für</strong><br />
λ = 1 genau den zentralen konkaven Bogen, <strong>der</strong> notwendig ist, um die konvexen<br />
Flanken zu verbinden. Für größere λ finden wir weitere akzeptable Lösungen mit<br />
Nullstellen im konkaven Bereich.<br />
Aus <strong>der</strong> Diskussion dieser Ergebnisse erwarten wir im Einklang mit systematischen<br />
Überlegung ein diskretes Spektrum<br />
0 < λ0 < λ1 < λ2 < . . . ,<br />
wobei die Eigenfunktion ϕn(ξ) zu λn genau n Nullstellen hat.<br />
38<br />
ϕ<br />
ξ
Numerische Lösungen von Gl. (98) <strong>für</strong> verschiedene λ. Im Bereich ξ 2 < λ ist y konkav zur<br />
Achse, außerhalb konvex. Die Rechnungen gehen von <strong>der</strong> Randbedingung ϕ(−∞) = 0 aus.<br />
Wenn auch ϕ(+∞) = 0 wird, ist λ Eigenwert.<br />
Nach diesen Vorüberlegungen wollen die Eigenwerte <strong>und</strong> Eigenfunktionen systematisch<br />
konstruieren. Dazu nehmen wir an, die Funktion y(ξ) erfülle bereits die<br />
Gleichung (98)<br />
y ′′ = (ξ 2 − λ)y<br />
mit den erfor<strong>der</strong>lichen Randbedingungen y(−∞) = y(∞) = 0, sei also (nicht<br />
normierte) Eigenfunktion zum Eigenwert λ. Dann bilden wir die Hilfsfunktion<br />
<br />
ˆy = ξ − d<br />
<br />
y = ξy − y<br />
dξ<br />
′ .<br />
Offenbar “erbt” ˆy die Randbedingungen von y. Um zu sehen, welche Differentialgleichung<br />
ˆy erfüllt, rechnen wir<br />
39
ˆy ′ = y + ξy ′ − y ′′ = ξy ′ + (λ + 1 − ξ 2 )y <strong>und</strong><br />
ˆy ′′ = ξy ′′ + y ′ + (λ + 1 − ξ 2 )y ′ − 2ξy<br />
= (λ + 2 − ξ 2 )y ′ − 2ξy + ξ(ξ 2 − λ)y<br />
= (λ + 2 − ξ 2 )(y ′ − ξy) = (ξ 2 − λ − 2)ˆy.<br />
Ist also y(ξ) Eigenfunktion zum Eigenwert λ, so ist ˆy(ξ) Eigenfunktion zum Eigenwert<br />
λ + 2.<br />
Mit dem Operator<br />
A − = ξ − d<br />
dξ<br />
können wir uns also ausgehend von einer Eigenfunktion ym(ξ) zum Eigenwertλm<br />
durch die Rekursion<br />
(99)<br />
yn+1 = A − yn = ξyn − y ′<br />
n , λn+1 = λn + 2 (100)<br />
eine unendliche Folge von Eigenfunktionen yn <strong>und</strong> Eigenwerten λn mit n > m<br />
konstruieren. Die definitive Übersicht über alle Eigenfunktionen <strong>und</strong> insbeson<strong>der</strong>e<br />
die Startlösung y0 erhalten wir, wenn wir neben A− auch den “adjungierten”<br />
Operator (vgl. S. 41)<br />
A + = ξ + d<br />
(101)<br />
dξ<br />
definieren. Er führt — bis auf einen unwesentlichen Faktor (s. u.) — von yn auf<br />
yn−1, also von λn auf λn−2. Um das zu sehen, kann man die obige Rechnung mit<br />
geän<strong>der</strong>tem Vorzeichen wie<strong>der</strong>holen. Eleganter <strong>und</strong> wesentlich informativer ist es<br />
jedoch, das Produkt<br />
A + A − = ξ 2 + 1 − d2<br />
= 1 + h (102)<br />
dξ2 zu bilden. Wenden wir diese Operatorgleichung auf yn an <strong>und</strong> berücksichtigen<br />
A − yn = yn+1, λn+1 = λn + 2 sowie hyn = λnyn, so folgt<br />
A + yn+1 = A + A − yn = (1 + h)yn = (λn + 1)yn<br />
yn−1 =<br />
1<br />
λn−1 + 1 A+ yn =<br />
40<br />
1<br />
o<strong>der</strong><br />
λn − 1 A+ yn. (103)
Und nun kommt <strong>der</strong> entscheidende Punkt: Mit Gl. (103) können wir uns ausgehend<br />
von einem beliebigen Eigenwert auf unserer “Leiter” “herunterhangeln”<br />
<strong>und</strong> immer kleinere Eigenwerte erzeugen. Da aber alle Eigenwerte positiv sein<br />
müssen, muß die Leiter (103) auf einer “untersten Sprosse” y0 enden — o<strong>der</strong> an<strong>der</strong>s<br />
ausgedrückt: A + y0 muß verschwinden. Daraus folgt die Differentialgleichung<br />
y ′ 0<br />
= −ξy0<br />
mit <strong>der</strong> (abgesehen von <strong>der</strong> Normierung) eindeutigen Lösung<br />
y0 = e −ξ2 /2 .<br />
Durch Einsetzen in (98) erhalten wir den zugehörigen Eigenwert λ0 = 1. Damit<br />
können wir alle Eigenfunktionen <strong>und</strong> Eigenwerte explizit angeben:<br />
<strong>und</strong><br />
λn = 2n + 1 o<strong>der</strong> En = (n + 1<br />
)¯hω (104)<br />
2<br />
y0 = e −ξ2 /2<br />
y1 = ξy0 − y ′ 0 = 2ξe−ξ2 /2<br />
y2 = ξy1 − y ′ 1 = (4ξ 2 − 2)e −ξ2 /2<br />
.<br />
yn+1 = ξyn − y ′ n . (105)<br />
Durch Induktion verifiziert man leicht, daß alle Eigenfunktionen die Form<br />
yn(ξ) = Hn(ξ)e −ξ2 /2<br />
(106)<br />
haben, wobei Hn(ξ) ein Polynom n-ten Grades in ξ (das Hermitesche Polynom)<br />
ist. yn hat entsprechend unserer Vorüberlegung genau n Nullstellen.<br />
Um nach den yn entwickeln zu können, müssen wir noch ihre Normierung berechnen.<br />
Die nötige Vorarbeit dazu haben wir bereits geleistet, es ist nämlich<br />
〈yn|yn〉 = 〈A − yn−1|A − yn−1〉 = 〈yn−1|A + A − |yn−1〉.<br />
Der letzte Schritt besagt, daß A + zu A − “adjungiert” ist <strong>und</strong> folgt aus <strong>der</strong> partiellen<br />
Integration<br />
<br />
dyn−1<br />
dξ yndξ<br />
<br />
= −<br />
41<br />
dyn<br />
yn−1<br />
dξ dξ.
Berücksichtigen wir nun noch A + A − = 1+h (vgl. (102)) <strong>und</strong> hyn−1 = λn−1yn−1 =<br />
(2n − 1)yn−1, so erhalten wir<br />
Mit dem Gr<strong>und</strong>integral<br />
folgt schließlich explizit<br />
〈yn|yn〉 = 2n〈yn−1|yn−1〉 o<strong>der</strong> 〈yn|yn〉 = 2 n n!〈y0|y0〉.<br />
<br />
〈y0|y0〉 =<br />
e −ξ2<br />
dξ = √ π<br />
〈yn|yn〉 = 2 n n! √ π. (107)<br />
Wenn wir es wünschen, können wir damit auch normierte Eigenfunktionen<br />
ϕn(ξ) =<br />
bilden, <strong>für</strong> die 〈ϕn|ϕm〉 = δnm gilt.<br />
1<br />
√ 2 n n!π 1/2 yn(ξ) (108)<br />
Die Eigenwerte <strong>und</strong> Eigenfunktionen sind in <strong>der</strong> folgenden Abbildung wie<strong>der</strong>gegeben.<br />
Eigenwerte <strong>und</strong> Eigenfunktionen des eindimensionalen<br />
harmonischen Oszillators. Die Parabel<br />
kennzeichnet das Potential u(ξ) = ξ 2 , das “Innere”<br />
<strong>der</strong> Parabel repräsentiert den klassisch erlaubten<br />
Bereich E ≥ V bzw. λ > ξ 2 . Die Eigenlösungen<br />
ϕn konzentrieren sich wesentlich<br />
auf diesen erlaubten Bereich, dringen aber etwas<br />
in den “verbotenen” Bereich ein <strong>und</strong> klingen<br />
dort exponentiell ab. Genau auf <strong>der</strong> Grenze<br />
V = E bzw. u = λ haben sie einen Wendepunkt.<br />
Wie sind diese Eigenfunktionen physikalisch zu interpretieren? Auf den allerersten<br />
flüchtigen Blick scheinen die entsprechenden Wellenfunktionen<br />
42
ψn(ξ, t) = ϕn(ξ)e −iωnt<br />
eine Zeitabhängigkeit zu zeigen, die <strong>der</strong> Frequenz<br />
ωn = En<br />
¯h<br />
= (n + 1<br />
2 )ω<br />
entspricht. Aber das ist natürlich nicht richtig, unsere Eigenfunktionen beschreiben<br />
ja nach Konstruktion(!) stationäre Zustände, bei denen<br />
gar nicht von <strong>der</strong> Zeit abhängt.<br />
Die erste Eigenfunktion<br />
|ψn(ξ, t)| 2 = ϕ 2 n (ξ)<br />
ψ0(x, t) = ϕ0(x)e −iω0t = π −1/4 e −ξ 2 /2 e − i<br />
2 ωt<br />
entspricht gerade einem Gaussschen Wellenpaket mit minimalem Unschärfeprodukt<br />
[vgl.(74)], <strong>und</strong> wir können diese Lösung tatsächlich “verstehen”, wenn wir<br />
von <strong>der</strong> klassischen Vorstellung eines Teilchens ausgehen, das “unten im Potentialtopf”<br />
ruht: x = 0, p = 0, E = p 2 /2m + kF x 2 /2 = 0. Nun wissen wir ja bereits,<br />
daß sich diese klassische Vorstellung nicht mit <strong>der</strong> Unschärferelation<br />
〈x 2 〉〈p 2 〉 ≥ ¯h2<br />
4<br />
verträgt. “Bestenfalls” können wir – eben mit einem Gaussschen Paket – ein<br />
Gleichheitszeichen erreichen <strong>und</strong> erhalten damit eine Energie<br />
E = kF<br />
2 〈x2 〉 + 1<br />
2m 〈p2 〉 = kF<br />
2 〈x2 〉 + ¯h2<br />
8m<br />
1<br />
〈x2 〉 .<br />
Diese Energie wird sowohl <strong>für</strong> große als auch <strong>für</strong> kleine 〈x 2 〉 groß. Für das Minimum<br />
rechnen wir<br />
Damit folgt<br />
dE<br />
d〈x2 kF<br />
=<br />
〉 2<br />
¯h2<br />
−<br />
8m<br />
1<br />
〈x 2 〉 2 = 0 o<strong>der</strong> 〈x2 〉 = ¯h<br />
2 √ mk .<br />
43
E = ¯h<br />
<br />
kF<br />
4 m<br />
<br />
¯h kF<br />
+<br />
4 m<br />
= ¯hω<br />
2<br />
= E0.<br />
Der Zustand |ψ0〉 mit <strong>der</strong> Energie E0 stellt also die “beste” mit <strong>der</strong> <strong>Quantenmechanik</strong><br />
verträgliche Annäherung an den klassischen harmonischen Oszillator dar,<br />
<strong>der</strong> nicht schwingt. Wir erhalten ein anschauliches Bild dieses Zustandes, wenn<br />
wir das im Potentialtopf ruhende Teilchen durch ein ausgeschmiertes Wellenpaket<br />
ersetzen.<br />
Die Vorsicht, mit <strong>der</strong> wir diesem Bild begegnen müssen, wird aber schon durch die<br />
“höheren” Eigenfunktionen deutlich. Hier ist nämlich <strong>der</strong> harmonische Oszillator<br />
mit einer höheren Energie En = (n+ 1<br />
)¯hω “angeregt”, sollte also schwingen. Aber<br />
2<br />
〈ψn|ψn〉 hängt gar nicht von <strong>der</strong> Zeit ab; was ist eine “stationäre Oszillation”?<br />
In <strong>der</strong> Abbildung auf <strong>der</strong> folgenden Seite ist die Aufenthaltswahrscheinlichkeit<br />
wn(ξ) = ψ∗ nψn = ϕ2 n <strong>für</strong> verschiedene n aufgetragen.<br />
Wir vergleichen wn(ξ) mit <strong>der</strong> mittleren Aufenthaltswahrscheinlichkeit w kl eines<br />
klassischen Teilchens <strong>der</strong> selben Energie im Potentialtopf des harmonischen Oszillators.<br />
Da jede Phase während einer Schwingung zweimal durchlaufen wird,<br />
gilt offenbar<br />
o<strong>der</strong> wegen dx/dt = v<br />
w kl (x)dx = 2 dt<br />
T<br />
w kl (x) = ω<br />
πv =<br />
= ω<br />
π dt<br />
ω<br />
π .<br />
2 (E − V ) m<br />
Übersetzen wir dies in unsere dimensionslose Darstellung [vgl. die Gleichungen<br />
(95) bis 97)], so erhalten erhalten wir die mittlere Aufenthaltswahrscheinlichkeit<br />
w kl<br />
n (ξ) =<br />
1<br />
π √ , (109)<br />
λn − ξ2 eines klassischen Oszillators <strong>der</strong> Energie En = λn¯hω/2 = (n + 1<br />
2 ¯hω.<br />
Diese Aufenthaltswahrscheinlichkeit ist in <strong>der</strong> Figur auf <strong>der</strong> folgenden Seite ebenfalls<br />
eingezeichnet. Für n = 0 <strong>und</strong> n = 1 zeigen die klassischen <strong>und</strong> quantenmechanischen<br />
Erwartungen noch wenig Ähnlichkeit. Mit wachsendem n fällt jedoch<br />
eine eigentümliche Entsprechung ins Auge: Offenbar oszilliert (nicht zeitlich, son<strong>der</strong>n<br />
örtlich!) die quantenmechanische Wahrscheinlichkeit wn um den klassischen<br />
Mittelwert wkl n . Für diese Oszillationen gibt es keine klassische Erklärung. Sie<br />
repräsentieren gerade die wellenmechanische Beson<strong>der</strong>heit <strong>und</strong> entsprechen dem<br />
Interferenzmuster hinter einem Doppelspalt.<br />
44
Aufenthaltswahrscheinlichkeit wn(ξ) des harmonischen Oszillators <strong>für</strong> verschiedene<br />
Energieeigenzustände n. Die konvexen Bögen repräsentieren die mittlere Aufenthaltswahrscheinlichkeit<br />
wkl n (ξ) [vgl. Gl. (109)] klassischer Oszillatoren <strong>der</strong> selben<br />
Energie.<br />
45
Ist also <strong>der</strong> quantenmechanische Erwartungswert generell ein Zeitmittel? Nein,<br />
das ist er keineswegs, aber die Energieeigenfunktionen haben schon etwas mit<br />
einem Zeitmittel zu tun. Wenn wir nämlich die Energie eines Oszillators exakt<br />
kennen, wissen wir wegen <strong>der</strong> Energie–Zeit–Unschärfe gar nichts mehr über den<br />
Zeitpunkt des Nulldurchgangs, also die Phase. Die Wahrscheinlichkeitsverteilung<br />
ψ ∗ nψn entspricht klassisch also <strong>der</strong> Aufenthaltswahrscheinlichkeit von isoenergetischen<br />
Oszillatoren beliebiger Phase, o<strong>der</strong> eben dem Zeitmittel.<br />
Kann unser quantenmechanischer Formalismus denn vielleicht die Dynamik, also<br />
die harmonische Schwingung, des harmonischen Oszillators gar nicht beschreiben?<br />
Zunächst einmal sehen wir an <strong>der</strong> Ehrenfest–Beziehung<br />
m〈¨x〉 = −〈 dV<br />
dx 〉 = kF 〈x〉 , (110)<br />
daß <strong>der</strong> Erwartungswert 〈x〉 des harmonischen Oszillators exakt die klassische<br />
Beziehung<br />
<br />
〈x〉 = a cos ωt + b sin ωt, ω = kF /m (111)<br />
erfüllt. [Das ist kein Wi<strong>der</strong>spruch zu den stationären Zuständen |ψn〉, denn <strong>für</strong><br />
die gilt<br />
(also a = b = 0), da alle ϕ 2 n<br />
〈x〉n = 〈ψn|x|ψn〉 = 0<br />
symmetrische Funktionen von x sind.]<br />
Also oszilliert <strong>der</strong> Oszillator auch quantenmechanisch genau mit <strong>der</strong> Frequenz<br />
ω. Eine solche Oszillation wird aber von den einzelnen Energieeigenfunktionen<br />
nicht beschrieben. Wir erhalten sie vielmehr erst dann, wenn wir verschiedene<br />
Eigenfunktionen gemäß<br />
ψ(ξ, t) = cnϕn(ξ)e −iωnt , ωn = (n + 1<br />
)ω (112)<br />
2<br />
überlagern. Dann sieht man sofort, daß die Wahrscheinlichkeitsdichte<br />
ψ ∗ ψ = <br />
c ∗ ncmϕn(ξ)ϕm(ξ)e i(n−m)ωt<br />
n,m<br />
<strong>und</strong> mit ihr alle Erwartungswerte<br />
〈A〉 = <br />
n,m<br />
c ∗ i(n−m)ωt<br />
ncm〈ϕn|A|ϕm〉e 46<br />
(113)
periodische Funktionen <strong>der</strong> Zeit mit <strong>der</strong> Periodendauer T = 2π/ω sind. Speziell<br />
zum Mittelwert 〈ξ〉 berechnen wir die “Matrixelemente”<br />
〈ϕn|ξ|ϕm〉 = 1<br />
2 〈ϕn|<br />
<br />
ξ + d<br />
<br />
d<br />
+ ξ − |ϕm〉<br />
dξ dξ<br />
= 1<br />
2 〈ϕn|(A + + A − )|ϕm〉<br />
= αn〈ϕn|ϕm−1〉 + βn〈ϕn|ϕm+1〉<br />
= αnδn,m−1 + βnδn,m+1 (114)<br />
(die Berechnung von αn <strong>und</strong> βn schenken wir uns) <strong>und</strong> erhalten<br />
〈ξ〉 = <br />
= <br />
c<br />
n,m<br />
∗ ncm(αnδn,m−1 + βnδn,m+1)e i(n−m)ωt<br />
n<br />
c ∗ n<br />
<br />
αncn+1e iωt + βncm−1e −iωt<br />
.<br />
〈ξ〉 wird also in Übereinstimmung mit (111) immer eine rein harmonische Funktion<br />
von ωt. Wenn wir also irgendein Wellenpaket im Potentialtopf des harmonischen<br />
Oszillators betrachten, so wird dessen “Schwerpunkt” — <strong>der</strong> Erwartungswert<br />
〈ξ〉 — rein harmonisch oszillieren, während sich die Form periodisch mit<br />
2π/ω — aber nicht rein harmonisch — verän<strong>der</strong>t. Lediglich das spezielle Gaußsche<br />
Wellenpaket, das ϕ0 entspricht, kann ohne Formverän<strong>der</strong>ung im Potentialtopf<br />
oszillieren (Übungen). Diese spezielle Lösung hat es vielen Physikern schwer<br />
gemacht, sich von <strong>der</strong> Vorstellung zu lösen, daß das Minimalpaket “wirklich” das<br />
Teilchen repräsentiert.<br />
Eine zeitlich oszillierende Wahrscheinlichkeitsdichte ψ ∗ ψ entspricht aber keiner<br />
exakt vorgegebenen Energie. Zu einer Beobachtung <strong>der</strong> Oszillation gehört nämlich<br />
eine Meßzeit δt < 1/ω, <strong>und</strong> die ist mit einer Energieunschärfe ∆E ∼ ¯h/δt > ¯hω<br />
verb<strong>und</strong>en. Zur Darstellung eines solchen Energiebereiches brauchen wir aber<br />
mehrere Energieeigenfunktionen. Eine scharfe Messung <strong>der</strong> Energie mit ∆E ≪ ¯hω<br />
erfor<strong>der</strong>t dagegen eine Meßzeit ∆t ≥ ¯h/∆E = 1/ω, also eine Beobachtung über<br />
viele Perioden. Und bei dieser Beobachtung sehen wir eben nur noch die über alle<br />
Phasen gemittelte Aufenthaltswahrscheinlichkeit des harmonischen Oszillators.<br />
Wir sind es aus <strong>der</strong> Atomphysik gewohnt, nur die stationären Zustände als relevante<br />
Lösungen <strong>der</strong> Schrödingergleichung zu betrachten: Nicht stationäre Lösungen<br />
sind viel zu “kurzlebig“, um uns genauer zu interessieren. Da es sich dabei<br />
meist um geladene Teilchen handelt, wird in nicht stationären Zuständen<br />
tatsächlich Energie abgestrahlt. Nichtstationarität wird daher als Übergang von<br />
einem stationären Zustand in einen an<strong>der</strong>en stationären Zustand beschrieben.<br />
47
Wenden wir diese Begriffe auf den harmonischen Oszillator an, beschreiben wir<br />
also die Schwingung durch Übergänge zwischen benachbarten Energieniveaus.<br />
Gl.(114) wird dann in <strong>der</strong> Sprechweise <strong>der</strong> Atomphysik als Auswahlregel ∆n = ±1<br />
interpretiert. Trägt <strong>der</strong> Oszillator eine elektrische Ladung, so strahlt er elektromagnetische<br />
Wellen <strong>der</strong> Frequenz ω ab. Die Auswahlregel ∆n = ±1 o<strong>der</strong> ∆E = ±¯hω<br />
läßt sich dann in die Aussage übersetzen, daß die ausgesandte (o<strong>der</strong> absorbierte)<br />
Strahlung in Photonen <strong>der</strong> Energie ¯hω gequantelt ist.<br />
3.3 Die Potentialmulde: Diskretes <strong>und</strong> kontinuierliches<br />
Spektrum<br />
Der harmonische Oszillator ist ein Modell <strong>für</strong> viele physikalische Systeme, in einer<br />
Hinsicht ist er aber immer unrealistisch: Bei hinreichend großem Abstand vom<br />
“Zentrum” wird schließlich jede Kraft verschwinden. Ein anziehendes Kraftzentrum<br />
wird daher i. a. durch eine Potentialmulde (Potentialtopf) mit V (±∞) = 0<br />
beschrieben:<br />
V(x)<br />
a b<br />
Ein klassisches Teilchen mit einer Energie E < 0 wird sich dann zwischen zwei<br />
Umkehrpunkten a <strong>und</strong> b bewegen <strong>und</strong> sich dabei qualitativ ähnlich wie <strong>der</strong> harmonische<br />
Oszillator verhalten. Eine entsprechende Analogie erwarten wir auch<br />
quantenmechanisch: Die stationäre Schrödingergleichung<br />
− ¯h2<br />
2m<br />
E
ϕn → Cn±e −κn|x| mit κn =<br />
<br />
−2mEn<br />
¯h 2 . (116)<br />
Für endlich tiefe Potentialtöpfe erwarten wir nun höchstens endlich viele Eigenwerte<br />
14 (siehe Skizze).<br />
E<br />
Ein entscheiden<strong>der</strong> Unterschied zum harmonischen Oszillator liegt darin, daß wir<br />
uns mit dieser Analogie auf geb<strong>und</strong>ene Zustände mit E < 0 beschränken müssen.<br />
Dem entsprechen klassisch oszillatorische Bahnen, die nicht aus <strong>der</strong> Potentialmulde<br />
herausführen. Für E ≥ 0 können jedoch die Teilchen über die Potentialmulde<br />
“hinweglaufen”. Die “stationäre” — was heißt das in dem Fall? — Schrödingergleichung<br />
(115) besitzt dann Lösungen, die statt (116) das asymptotische Verhalten<br />
ϕE>0 → αe ikx + βe −ikx , k =<br />
ϕ<br />
E 0<br />
E 1<br />
E 2<br />
<br />
2mE<br />
¯h 2<br />
x<br />
(117)<br />
<strong>für</strong> x → ±∞ zeigen. Das sind natürlich genau die ebenen Wellen, die uns zur<br />
kräftefreien Schrödingergleichung geführt hatten <strong>und</strong> die ausdrücken, daß <strong>der</strong><br />
Impuls p = ¯hk konstant bleibt.<br />
Dieser im Gr<strong>und</strong>e nicht unerwarteter Sachverhalt führt zu einer unangenehmen<br />
mathematischen Schwierigkeit: Funktionen mit dem asymptotischen Verhalten<br />
(117) sind nicht normierbar <strong>und</strong> damit keine Eigenfunktionen im bisherigen strengen<br />
Sinn. Wir benötigen sie aber, um allgemeinere Lösungen <strong>der</strong> Schrödingergleichung<br />
— z. B. Wellenpakete — darzustellen: Der diskrete Satz normierbarer<br />
Eigenfunktionen ist nicht vollständig!<br />
Mathematisch kann man nun die “Eigenfunktionen” <strong>für</strong> E > 0 durch geeignete<br />
Grenzprozesse aus normierbaren Eigenfunktionen darstellen. Beispielsweise kann<br />
man das Potential V (x) durch<br />
14 Wir entnehmen alle diese Aussagen <strong>der</strong> elementaren Anschauung <strong>und</strong> verzichten auf die<br />
mathematischen Beweise.<br />
49
VA(x) =<br />
<br />
V (x) <strong>für</strong> |x| < A<br />
∞ <strong>für</strong> |x| > A<br />
−A A<br />
ersetzen <strong>und</strong> den Grenzübergang A → ∞ betrachten. Für jedes endliche A erhält<br />
man dann ein vollständiges diskretes Spektrum. Mit wachsendem A rücken die<br />
Eigenwerte Eν > 0 jedoch immer dichter zusammen <strong>und</strong> in <strong>der</strong> Grenze A = ∞<br />
erhalten wir ein kontinuierliches Spektrum: Alle Energiewerte E ≥ 0 werden<br />
Eigenwerte.<br />
Mathematisch benötigt man nun das Konzept <strong>der</strong> “Distributionen”, um den Hilbertraum<br />
<strong>für</strong> solche Grenzprozesse zu vervollständigen. Wir verzichten auf die<br />
mathematische Rechtfertigung <strong>und</strong> interpretieren die freien Zustände E ≥ 0 physikalisch:<br />
Wenn ein Teilchen nicht mehr geb<strong>und</strong>en ist, so kann es sich irgendwo im<br />
gesamten Raum aufhalten, die Aufenthaltswahrscheinlichkeit in jedem endlichen<br />
Teilinterval <strong>und</strong> damit die Wahrscheinlichkeitsdichte wird also Null. Wir können<br />
aber immer noch nach einer ortsabhängigen Intensität ψ ∗ ψ fragen, wenn wir nicht<br />
von einem Teilchen, son<strong>der</strong>n von einem Strom von Teilchen bestimmter Energie,<br />
welcher den ganzen Raum erfüllt, ausgehen. Dies entspricht genau <strong>der</strong> experimentellen<br />
Situation bei den Interferenzexperimenten <strong>und</strong> führt uns zur Einführung<br />
einer nicht normierbaren Wellenfunktion<br />
Φk(x) = √ ne ikx<br />
V<br />
x<br />
(118)<br />
freier Teilchen. Nach Gl. (55) gehört zu dieser Wellenfunktion eine Stromdichte<br />
j = ¯h<br />
<br />
2im<br />
Φ ∗ k<br />
d<br />
dx Φk<br />
d<br />
− Φk<br />
dx Φ∗ k<br />
<br />
= ¯h 2ik<br />
n o<strong>der</strong><br />
2im<br />
j = ¯hk p<br />
n =<br />
m m n = nvkl. (119)<br />
Gl. (118) beschreibt also einen Strom von Teilchen <strong>der</strong> Dichte n, die mit <strong>der</strong><br />
Geschwindigkeit vkl = p/m strömen. Entsprechend beschreibt<br />
Φ−k(x) = √ ne −ikx<br />
eine Welle o<strong>der</strong> einen Teilchenstrom in negativer x–Richtung o<strong>der</strong> allgemeiner<br />
50<br />
(120)
Φk(r) = √ ne ik·r<br />
eine Welle o<strong>der</strong> einen Strom in k–Richtung.<br />
(121)<br />
Mit Φ ∗ kΦk = n = const. verstehen wir auch sofort, warum Φk nicht normierbar sein<br />
kann: ein unendlich ausgedehnter Strom von Teilchen konstanter Dichte enthält<br />
nun einmal unendlich viele Teilchen! Abschließend bleibt lediglich zu erwähnen,<br />
daß wir bei einer präzisen Diskussion — wie bereits früher betont — die Begriffe<br />
“Teilchendichte” <strong>und</strong> “Stromdichte” genauer durch “Wahrscheinlichkeits–Dichte”<br />
<strong>und</strong> “Wahrscheinlichkeits–Stromdichte” ersetzen sollten.<br />
Nach dieser physikalischen Erklärung können wir nun also Funktionen, die sich<br />
im Unendlichen wie<br />
ϕk(x) = e ikx<br />
(122)<br />
verhalten, als Eigenfunktionen 15 zulassen: sie beschreiben uns einen Teilchenstrom<br />
<strong>der</strong> Dichte 1 <strong>und</strong> <strong>der</strong> Geschwindigkeit vkl = p/m = ¯hk/m.<br />
Wenn wir nun auf die asymptotische Form (117) <strong>der</strong> Energie–Eigenfunktionen<br />
zurückkommen, so haben wir die Freiheit, zwei willkürliche Konstanten α <strong>und</strong><br />
β festzulegen. Diese Konstanten bestimmen die Intensität einer vor– <strong>und</strong> einer<br />
rücklaufenden Welle. Um hier Eindeutigkeit zu erzielen, wollen wir gr<strong>und</strong>sätzlich<br />
die folgende Verfügung treffen. (Dabei denken wir nicht nur an Potentialmulden,<br />
son<strong>der</strong>n auch an Berge <strong>und</strong> allgemeine Störungen.)<br />
Wir nehmen an, daß von links (x = −∞) eine ebene Welle ϕe = exp(ikx) einläuft<br />
(“Ursache”). Diese Welle repräsentiert einen Teilchenstrom <strong>der</strong> Dichte 1 <strong>und</strong> <strong>der</strong><br />
Stromdichte je = ¯hk/m in positiver x–Richtung. Als “Wirkung” erscheint weit<br />
hinter <strong>der</strong> Potentialstörung (x → +∞) eine auslaufende Welle ϕa = d exp(ikx).<br />
Aus <strong>der</strong> Analogie zur Optik, wo das verän<strong>der</strong>liche Potential einem verän<strong>der</strong>lichen<br />
Brechungsindex entspricht, schließen wir, daß wir links (x → −∞) außerdem eine<br />
reflektierte Welle ϕr = r exp(−ikx) zulassen müssen — auch wenn dies im klaren<br />
Wi<strong>der</strong>spruch zur klassischen Mechanik steht. Wir suchen also <strong>für</strong> E > 0 diejenige<br />
Lösung <strong>der</strong> stationären Schrödingergleichung (115), welche die asymptotische<br />
Darstellung<br />
ϕ → e ikx + re −ikx<br />
ϕ → de ikx<br />
(x → −∞)<br />
(x → +∞), k =<br />
<br />
2mE<br />
¯h 2<br />
(123)<br />
15 Für freie Teilchen sind dies gemeinsame Eigenfunktionen des Impuls– <strong>und</strong> Hamiltonopera-<br />
tors.<br />
51
esitzt. Gl. (123) wird auch als Ausstrahlungsbedingung bezeichnet. (Die Bedeutung<br />
dieser Bedingung wird in <strong>der</strong> dreidimensionalen Verallgemeinerung noch<br />
transparenter.) Aus den Stromdichten ja = d ∗ d¯hk/m <strong>und</strong> jr = −r ∗ r¯hk/m <strong>der</strong><br />
auslaufenden <strong>und</strong> <strong>der</strong> reflektierten Teilchen ergeben sich dann die Koeffizienten<br />
D(E) = ja<br />
<strong>der</strong> Durchlässigkeit <strong>und</strong> <strong>der</strong> Reflexion.<br />
je<br />
= d ∗ d <strong>und</strong> R(E) = |jr|<br />
3.4 Das eindimensionale Kastenpotential<br />
je<br />
= r ∗ r (124)<br />
Wir wollen das allgemeine Konzept des vorigen Abschnitts an einem Beispiel<br />
verdeutlichen <strong>und</strong> wählen dazu — da die Fälle, in denen die Schrödingergleichung<br />
elementar lösbar ist, rar sind — das einfache Kastenpotential<br />
V (x) =<br />
−a<br />
<br />
V0 <strong>für</strong> |x| ≤ a<br />
0 <strong>für</strong> |x| > a .<br />
V<br />
V 0<br />
a<br />
x<br />
(125)<br />
In klassischer Beschreibung ist das Teilchen also <strong>für</strong> |x| = a überall kräftefrei <strong>und</strong><br />
erfährt nur bei x = ±a eine (unendlich) starke Kraft.<br />
Mit<br />
ɛ = 2mE<br />
¯h 2 <strong>und</strong> u(x) = 2m<br />
2 V (x)<br />
¯h<br />
lautet die stationäre Schrödingergleichung<br />
52
d2ϕ + [ɛ − u(x)]ϕ = 0. (126)<br />
dx2 Wir setzen (bis auf weiteres) u0 = 2mV0/¯h 2 < 0 voraus <strong>und</strong> interessieren uns<br />
zunächst <strong>für</strong> die diskreten Eigenwerte ɛn < 0 mit normierbaren Eigenfunktionen<br />
ϕn.<br />
Aus Gl. (126) entnehmen wir nun die allgemeine Lösung<br />
außerhalb <strong>und</strong><br />
ϕ =<br />
<br />
αe κx (x < −a)<br />
βe −κx (x > a)<br />
<br />
mit κ = √ −ɛ (127)<br />
ϕ = γ cos(kx) + δ sin(kx) (|x| ≤ a) mit k = √ ɛ − u0 (128)<br />
innerhalb des Potentialtopfes. Zur Bestimmung <strong>der</strong> vier Unbekannten α, β, γ, δ<br />
haben wir nun fünf Bedingungen, nämlich<br />
– die Stetigkeit 16 von ϕ bei x = ±a<br />
– die Stetigkeit von ϕ ′ bei x = ±a <strong>und</strong><br />
– die (willkürliche) Normierung von ϕ.<br />
Dies ist i. a. eine Bedingung zuviel; daher werden wir nur <strong>für</strong> bestimmte Werte<br />
von E — eben die Eigenwerte En — Lösungen finden.<br />
Die eigentliche Rechnung können wir durch folgende Überlegung abkürzen: Aufgr<strong>und</strong><br />
<strong>der</strong> Symmetrie des Problems erwarten wir, daß die Aufenthaltswahrscheinlichkeit<br />
ϕ 2 nur von |x| abhängt. Das bedeutet aber, daß wir entwe<strong>der</strong> symmetrische<br />
Eigenfunktionen<br />
ϕ = e −κ|x| <strong>für</strong> |x| > a <strong>und</strong> ϕ = γ cos(kx) <strong>für</strong> |x| ≤ a (129)<br />
o<strong>der</strong> antisymmetrische Eigenfunktionen<br />
ϕ = sign(x)e −κ|x| <strong>für</strong> |x| ≥ a <strong>und</strong> ϕ = δ sin(kx) <strong>für</strong> |x| ≤ a (130)<br />
16 Die Stetigkeit von ϕ <strong>und</strong> ϕ ′ läßt sich ebensowenig wie ϕ selbst physikalisch interpretieren<br />
<strong>und</strong> begründen. Wir folgern sie mathematisch aus <strong>der</strong> Beschränkheit von ϕ ′′ .<br />
53
erhalten. Über die Normierung haben wir mit dem Vorfaktor 1 vor <strong>der</strong> Exponentialfunktion<br />
bereits verfügt. Daher stehen uns zur Bestimmung <strong>der</strong> einen Konstante<br />
γ bzw. δ nun die zwei Stetigkeitsbedingungen bei x = +a zur Verfügung.<br />
Betrachten wir zunächst die symmetrischen Eigenfunktionen. Für sie erhalten wir<br />
e −κa = γ cos(ka) <strong>und</strong> − κe −κa = −kγ sin(ka).<br />
Diese beiden Gleichungen können im allgemeinen nur <strong>für</strong> bestimmte Werte von<br />
κ(ɛ) <strong>und</strong> k(ɛ) erfüllt sein. Eliminieren wir nämlich γ, so erhalten wir (nach Erweiterung<br />
mit a) die Bedingung<br />
ka tan(ka) = κa. (131)<br />
Entsprechend erhalten wir <strong>für</strong> die antisymmetrischen Eigenfunktionen die beiden<br />
Gleichungen<br />
e −κa = δ sin(ka) <strong>und</strong> − κe −κa = kδ cos(ka),<br />
die auf die Bedingung<br />
führen.<br />
−ka cot(ka) = κa (132)<br />
Wir können die Auswertung <strong>der</strong> verschiedenen Bedingungen (131) <strong>und</strong> (132) zusammenfassen,<br />
wenn wir berücksichtigen,<br />
– daß tan x <strong>und</strong> cot x mit π periodisch sind <strong>und</strong><br />
– daß tan(x − π/2) = − cot x gilt.<br />
Damit lassen sich sowohl (131) als auch (132) in <strong>der</strong> Form<br />
<br />
κa = ka tan<br />
ka − m π<br />
2<br />
<br />
, m = 0, 1, 2, . . . (133)<br />
schreiben, wobei m alle natürlichen Zahlen einschlielich 0 durchläuft, wenn wir<br />
das Argument des Tangens auf das Intervall [0, π/2] beschränken. Die Eigenwerte<br />
erhalten wir graphisch, indem wir (133) mit dem Kreisbogen<br />
κ 2 + k 2 = −u0 o<strong>der</strong> a 2 κ 2 + a 2 k 2 = R 2 mit R 2 = a 2 |u0| = 2ma2<br />
¯h 2 |V0|<br />
vergleichen (siehe die folgende Abbildung).<br />
54
Graphische Lösung <strong>der</strong> Eigenwertgleichung<br />
(133): κa als Funktion<br />
von ka wird mit dem Kreisbogen<br />
a 2 κ 2 +a 2 k 2 = R 2 = −a 2 u0 verglichen.<br />
(Die Abbildung bezieht sich<br />
speziell auf R = 5, also a 2 u0 =<br />
−25.)<br />
Für kleine Werte von R erhalten wir genau einen Eigenwert. Lassen wir R nun<br />
anwachsen, so entsteht jeweils ein zusätzlicher Eigenwert, wenn R die Grenze<br />
mπ/2 überschreitet. Wir erhalten so eine endliche Anzahl<br />
⎡<br />
<br />
2R<br />
N = 1 + = 1 + ⎣<br />
π<br />
2<br />
<br />
2ma<br />
π<br />
2<br />
¯h 2 ⎤<br />
|V0| ⎦ (134)<br />
von Eigenwerten, die von V0a 2 abhängt. Diese Zahl können wir aus <strong>der</strong> wellenmechanischen<br />
Anschauung “verstehen”: Teilchen im Potentialtopf haben einen<br />
maximalen Impuls<br />
p0 =<br />
Dem entspricht eine minimale Wellenlänge<br />
λ0 = 2π¯h<br />
Damit können wir (134) auch in <strong>der</strong> Form<br />
p0<br />
<br />
2m|V0|.<br />
= 2π¯h<br />
<br />
2m|V0| .<br />
<br />
4a<br />
N = 1 +<br />
λ0<br />
(135)<br />
schreiben: Die Zahl <strong>der</strong> Eigenwerte ist gleich eins plus die Anzahl <strong>der</strong> Halbwellen<br />
(λ0/2), die in <strong>der</strong> Topfbreite (2a) “passen”. Die “zusätzliche” eins ergibt sich<br />
daraus, daß die Welle noch ein Stück (mit exponentieller Dämpfung) in den “verbotenen”<br />
Bereich außerhalb des Potentialtopfes eindringt (vgl. die Figur auf <strong>der</strong><br />
nächsten Seite).<br />
55
Eigenwerte <strong>und</strong> –funktionen im Kastenpotential <strong>für</strong> a 2 u0 = −20 <strong>und</strong> a 2 u0 = −25.<br />
Bei festem a erhalten wir nur <strong>für</strong> V0 → −∞ (unendlich tiefer Potentialtopf)<br />
unendlich viele Eigenwerte<br />
akn = n π<br />
2<br />
o<strong>der</strong> ɛn − u0 =<br />
Hierzu gehören die Eigenfunktionen<br />
<br />
nπ 2<br />
, n = 1, 2, 3, . . . (136)<br />
2a<br />
ϕ2m = sin(k2mx) bzw. ϕ2m+1 = cos(k2m+1x) (137)<br />
mit Nullstellen am Rand des Potentialtopfes: Mit −V0 gehen auch −E <strong>und</strong> κ<br />
gegen ∞, die Welle kann dann nicht mehr in die unendlich hohe Potentialwand<br />
eindringen.<br />
Kehren wir nun zu endlichen Potentialwerten V0 zurück <strong>und</strong> betrachten die freien<br />
Teilchen mit E > 0. Entsprechend Gl. (123) setzen wir nun 17<br />
ϕ =<br />
<br />
e ikx + re −ikx (x < −a)<br />
de ikx (x > a)<br />
<br />
mit k = √ ɛ (138)<br />
<strong>für</strong> das Potential außerhalb des Potentialtopfes an. Im Potentialtopf (|x| ≤ a) gilt<br />
dagegen<br />
ϕ = ãe ik0x + ˜ be −ik0x mit k0 = √ ɛ − u0. (139)<br />
17 Zur anschaulichen Interpretation ist es nützlich, das entsprechende optische Problem zu<br />
diskutieren. Der Bereich |x| < a entspricht dann einem Bereich mit verän<strong>der</strong>tem Brechungsindex.<br />
56
Die vier unbekannten Koeffizienten r, d, ã, ˜ b müssen wir nun aus <strong>der</strong> Stetigkeit<br />
von ϕ <strong>und</strong> ϕ ′ bei x = a <strong>und</strong> x = −a bestimmen, also aus 18<br />
ãe ik0a + ˜ be −ik0a = de ika<br />
k0(ãe ik0a − ˜ be −ik0a ) = kde ika<br />
ãe −ik0a + ˜ be ik0a = e −ika + re ika<br />
k0(ãe −ik0a − ˜ be ik0a ) = k(e −ika − re ika ). (140)<br />
Wir schenken uns nicht nur die langwierige Lösung dieser Gleichungen, son<strong>der</strong>n<br />
verzichten auch auf die wenig erhellende Anschrift <strong>der</strong> Ergebnisse (vgl. Süßmann<br />
S. 50/51, Gleichungen (28, 29) mit L = 2a <strong>und</strong> kK = k0). Wichtig sind uns nur<br />
die folgenden beiden Feststellungen:<br />
1. Wir haben vier lineare Gleichungen zur Bestimmung <strong>der</strong> vier Koeffizienten<br />
r, d, a <strong>und</strong> b. Im Gegensatz zum Fall E < 0 ist unser Gleichungssystem <strong>für</strong><br />
E > 0 also nicht überbestimmt. Darum gibt es nicht nur <strong>für</strong> bestimmte E<br />
Lösungen, son<strong>der</strong>n wir erhalten ein kontinuierliches Spektrum.<br />
2. Nach <strong>der</strong> klassischen Mechanik sollten alle Teilchen über die Potentialmulde<br />
weglaufen. Dem entspricht D = d ∗ d = 1 <strong>und</strong> R = r ∗ r = 0. Setzen wir jedoch<br />
r = 0, so folgt mit z = e ik0a aus den beiden letzten Gleichungen (140)<br />
ã<br />
z + ˜bz = k0<br />
<br />
ã<br />
k z − ˜ <br />
bz .<br />
Nach den ersten beiden Gleichungen (140) gilt außerdem<br />
ãz + ˜ b<br />
z<br />
= k0<br />
k<br />
<br />
ãz − ˜ <br />
b<br />
.<br />
z<br />
Diese beiden linearen homogenen Gleichungen besitzen aber nur <strong>für</strong> z 2 =<br />
1/z 2 o<strong>der</strong> z 4 = 1 nicht–triviale Lösungen ã <strong>und</strong> ˜ b. Wir schließen daraus,<br />
daß — abgesehen von “Resonanzen” e ik0a = ±1 <strong>und</strong> ±i o<strong>der</strong> k0a = nπ/2<br />
— immer ein gewisser Bruchteil von Teilchen an <strong>der</strong> Potentialmulde reflektiert<br />
wird. [Ist die Resonanzbedingung erfüllt, so entspricht die Breite des<br />
Potentialtopfes gerade einer ganzen Zahl von halben Wellenlängen. Dabei<br />
löschen sich die bei x = +a <strong>und</strong> bei x = −a reflektierten Wellen durch<br />
Interferenz.]<br />
18 Da das Problem durch die Randbedingungen nicht mehr symmetrisch ist, ist es rechnerisch<br />
günstiger, den Potentialtopf in den Bereich (0, 2a) zu legen.<br />
57
3.5 Potentialbarriere <strong>und</strong> Tunneleffekt<br />
Wir haben bisher von einer Potentialmulde gesprochen, unsere Diskussion <strong>der</strong><br />
“Streuung” (E > 0) gilt aber ohne jede Än<strong>der</strong>ung genauso <strong>für</strong> einen Potentialberg<br />
V0 > 0 — vorausgesetzt, es gilt E > V0, so daß k0 in Gl. (139) reell ist. Noch<br />
viel interessanter ist jedoch <strong>der</strong> Fall E < V0, <strong>der</strong> klassisch eine <strong>und</strong>urchdringliche<br />
Potentialbarriere darstellt, an <strong>der</strong> alle Teilchen reflektiert werden.<br />
−a<br />
V<br />
E<br />
0 a x<br />
Statt <strong>der</strong> Gl. (139) erhalten wir nun im “verbotenem” Bereich |x| < a<br />
ϕ = ãe −κ0x + ˜ be κ0x mit κ0 = √ u0 − ɛ. (141)<br />
Aber auch nun können wir auf dieselbe Rechnung zurückgreifen, wenn wir nur<br />
k0 durch iκ0 ersetzen (k0 <strong>und</strong> κ0 sind jeweils reell). Auch in diesem Fall erhalten<br />
wir also eine endliche Wahrscheinlichkeit D = d ∗ d da<strong>für</strong>, daß das Teilchen die<br />
Barriere durchdringt: Das Teilchen gräbt sich bildlich durch den Potentialberg,<br />
man spricht vom Tunnel–Effekt. Führt man die Rechnung explizit aus, so erhält<br />
man den Durchlaßkoeffizienten<br />
D(E) = d ∗ d =<br />
g(E) =<br />
<br />
<br />
1 +<br />
<br />
2<br />
−1<br />
V0 g(E)<br />
4E|V0 − E|<br />
sin 2 (2k0a) (E > V0)<br />
sinh 2 (2κ0a) (E < V0) .<br />
mit (142)<br />
Für hohe <strong>und</strong> breite Potentialbarrieren, die schwer zu durchtunneln sind, gilt<br />
g(E) ≈ 1<br />
4 e4κ0a , <strong>und</strong> die Tunnelwahrscheinlichkeit wird<br />
D(E) = 16E(V0 − E)<br />
V 2 e<br />
0<br />
−4κ0a 2<br />
mit κ0 = 2m<br />
¯h 2 (V0 − E). (143)<br />
58
Der bestimmende Exponent geht also mit <strong>der</strong> Breite des Potentialberges <strong>und</strong> <strong>der</strong><br />
Wurzel aus <strong>der</strong> “Fehlenergie” V0 − E. Den Exponentialfaktor verstehen wir aus<br />
<strong>der</strong> Struktur von Gl. (141): Wir erwarten eine Lösung, die im verbotenem Bereich<br />
von links nach rechts exponentiell abklingt, d. h. es muß<br />
ϕ(a) ∼ e −2κ0a ϕ(−a)<br />
gelten. Da die Aufenthaltswahrscheinlichkeit <strong>und</strong> <strong>der</strong> Strom mit ϕ ∗ ϕ geht, folgt<br />
hier<strong>für</strong> <strong>der</strong> Faktor exp(−4κ0a).<br />
Wir erwähnen abschließend, daß <strong>der</strong> dominierende Exponentialfaktor <strong>für</strong> ortsabhängige<br />
Potentiale annähernd (“WBK–Näherung”) in<br />
D(E) ∼ e<br />
<br />
x1 −2 κ(x)dx<br />
x 0<br />
mit κ(x) =<br />
<br />
2m<br />
2 (V (x) − E) (144)<br />
¯h<br />
übergeht. Dabei sind x0 <strong>und</strong> x1 die Grenzen des klassisch verbotenen Bereichs.<br />
Als Beispiele <strong>für</strong> Phänomene, die auf dem Tunnel–Effekt beruhen, nennen wir den<br />
α–Zerfall <strong>und</strong> die Elektronen–Feldemission aus Metallen. Ein optisches Analogon<br />
läßt sich bei <strong>der</strong> Totalreflexion an Schichten endlicher Dicke finden.<br />
3.6 Kugelsymmetrische Potentiale im dreidimensionalen<br />
Raum<br />
Bisher haben wir nur eindimensionale Lösungen <strong>der</strong> Schrödingergleichung diskutiert.<br />
Wir befassen uns nun mit <strong>der</strong> dreidimensionalen stationären Schrödingengleichung<br />
mit isotropem Hamiltonoperator<br />
H = p2<br />
+ V (r). (145)<br />
2m<br />
Dabei beschränken wir uns auf die Diskussion geb<strong>und</strong>ener Zustände 19 E < 0. Dies<br />
setzt natürlich attraktive Potentiale V (r) voraus. Wir nehmen darüber hinaus an,<br />
daß das Potential <strong>für</strong> r → ∞ verschwindet <strong>und</strong> gehen von<br />
aus.<br />
V (r) < V (∞) = 0<br />
19 Die freien Zustände E > 0 werden in <strong>der</strong> Streutheorie behandelt. Diese sprengt schon allein<br />
wegen ihres Umfangs den Rahmen unserer Darstellung.<br />
59
Das kugelsymmetrische Potential legt es nun nahe, die stationäre Schrödingergleichung<br />
− ¯h2<br />
∆χ + V (r)χ = Eχ (146)<br />
2m<br />
in sphärischen Polarkoordinaten r, ϑ, ϕ anzuschreiben. Dazu benötigen wir die<br />
Darstellung<br />
∆ = 1<br />
r<br />
∂ 2<br />
r +<br />
∂r2 1<br />
r 2 sin ϑ<br />
∂ ∂<br />
sin ϑ<br />
∂ϑ ∂ϑ +<br />
1<br />
r 2 sin 2 ϑ<br />
∂2 ∂ϕ2 des Laplaceoperators, die wir einer Formelsammlung entnehmen. Wenn wir zur<br />
bequemen Anschrift noch<br />
µ = cos ϑ<br />
einführen, erhalten wir so die Schrödingergleichung<br />
− ¯h2<br />
2m<br />
1<br />
r<br />
∂ 2<br />
¯h2<br />
rχ −<br />
∂r2 2mr2 <br />
∂<br />
∂µ (1 − µ2 ) ∂χ 1<br />
+<br />
∂µ 1 − µ 2<br />
[V (r) − E]χ = 0.<br />
Zur Lösung versuchen wir einen Separationsansatz<br />
<strong>und</strong> erhalten<br />
−u<br />
∂<br />
∂µ (1 − µ2 ) ∂Y<br />
∂µ<br />
∂2χ ∂ϕ2 <br />
+ (147)<br />
rχ(r, ϑ, ϕ) = u(r)Y (ϑ, ϕ) (148)<br />
1<br />
+<br />
1 − µ 2<br />
∂2Y ∂ϕ2 <br />
= r 2 Y<br />
<br />
u ′′ + 2m<br />
<br />
2 (E − V )u<br />
¯h<br />
Nach Division durch uY hängt die linke Seite nur von den Winkeln <strong>und</strong> die<br />
rechte nur von r ab. Beide sind also gleich einer Konstante λ. Damit zerfällt die<br />
Schrödingergleichung in eine radiale Gleichung<br />
<strong>und</strong> eine Gleichung<br />
d2u 2m<br />
λ<br />
+<br />
dr2 2 (E − V )u − u = 0 (149)<br />
¯h r2 60<br />
.
∂<br />
∂µ (1 − µ2 ) ∂Y<br />
∂µ<br />
+ 1<br />
1 − µ 2<br />
∂2Y + λY = 0. (150)<br />
∂ϕ2 Wir stellen die radiale Gleichung zunächst zurück. Gl.(150) läßt sich durch eine<br />
weitere Separation<br />
behandeln:<br />
Φ(1 − µ 2 )<br />
Y (ϑ, ϕ) = P (µ)Φ(ϕ)<br />
d<br />
dµ (1 − µ2 ) dP<br />
dµ<br />
+ λP<br />
<br />
= −P d2Φ .<br />
dϕ2 Nach Division durch P Φ hängt nun die linke Seite nur von µ, die rechte nur von<br />
ϕ ab. Beide sind also konstant, die Konstante nennen wir m 2 :<br />
d<br />
dµ (1 − µ2 ) dP<br />
dµ +<br />
<br />
λ − m2<br />
1 − µ 2<br />
<br />
P = 0 (151)<br />
Gleichung (152) können wir sogleich lösen:<br />
d 2 Φ<br />
dϕ 2 + m2 Φ = 0. (152)<br />
Φm(ϕ) = e imϕ . (153)<br />
Dabei verlangt die Eindeutigkeit Φ(ϕ + 2π) = Φ(ϕ), daß m ganzzahlig ist: m =<br />
0, ±1, ±2 . . .<br />
Die Untersuchung <strong>der</strong> Gl. (151) ist wesentlich aufwendiger. Es stellt sich heraus,<br />
daß reguläre Lösungen nur <strong>für</strong><br />
λ = l(l + 1) (154)<br />
existieren, wobei l eine ganze Zahl ≥ |m| ist. Die regulären Lösungen P m<br />
l (µ)<br />
heißen Legendre– o<strong>der</strong> Kugel–Funktionen. Zusammengefaßt erhalten wir also<br />
Winkelfunktionen<br />
Ylm(ϑ, ϕ) = clmP m<br />
l (cos ϑ)e imϕ<br />
mit l = 0, 1, 2, 3 . . .<br />
<strong>und</strong> m = −l, −l+1, . . . , l−1, l.<br />
61<br />
(155)
Dabei sind clm geeignete Normierungsfaktoren, die durch<br />
<br />
Y ∗<br />
lmYl ′ m ′ sin ϑdϑdϕ = δll ′δmm ′<br />
definiert sind. Die Ylm sind als Kugelflächen–Funktionen bekannt, in niedrigster<br />
Ordnung erhält man<br />
Y0 0 = (4π) −1/2 , Y1 0 =<br />
1/2<br />
1/2<br />
3<br />
3<br />
cos ϑ, Y1 ±1 = sin ϑ e<br />
4π<br />
8π<br />
±iϕ .<br />
Bevor wir uns nun die radiale Gleichung (149) ansehen, wollen wir versuchen,<br />
den Winkelanteil physikalisch zu interpretieren. Dazu gehen wir noch einmal zur<br />
Problemstellung mit dem Hamiltonoperator (145) zurück <strong>und</strong> erinnern uns an<br />
das Zentralkraftproblem <strong>der</strong> klassischen Mechanik.<br />
Dort hatten wir ausgenutzt, daß <strong>der</strong> Drehimpuls<br />
L = r × p<br />
konstant ist <strong>und</strong> hatten die Bewegung in <strong>der</strong> Ebene senkrecht zu L untersucht.<br />
Dabei erhielten wir radial ein eindimensionales Bewegungsproblem mit einem<br />
effektiven Potential ˜ V = V +L 2 /2mr 2 . Wir erkennen dies koordinatenunabhängig<br />
aus<br />
L 2 = L · (r × p) = r · (p × L) = r · [p × (r × p]<br />
Es gilt also p 2 = L 2 /r 2 + p 2 r <strong>und</strong><br />
= r · [p 2 r − p · r p] = p 2 r 2 − (p · r) 2 .<br />
H = p2r L2<br />
+ + V (r). (156)<br />
2m 2mr2 Das liefert in radialer Richtung eine eindimensionale Bewegungsgleichung, mit<br />
einem “zusätzlichen Potential” L 2 /2mr 2 <strong>für</strong> die Fliehkraft.<br />
Quantenmechanisch ist die obige Rechnung nun nicht ohne weiteres gültig, weil<br />
die Reihenfolge <strong>der</strong> Operatoren r, p <strong>und</strong> L beachtet werden muß. Unter sorgfältiger<br />
Beachtung <strong>der</strong> entsprechenden Vertauschungsrelationen (s. Messiah Bd. I,<br />
Abschn. 9.1.1) o<strong>der</strong> durch direktes Ausmultiplizieren von L 2 = L 2 x + L2 y + L2 z läßt<br />
sich aber zeigen, daß Gl. (156) als quantenmechanische Operatorgleichung mit<br />
dem Drehimpuls [vgl. (63)]<br />
62
L = r × p = ¯h<br />
r × ∇ (157)<br />
i<br />
gilt, wenn man den “radialen Impuls” durch den Operator<br />
definiert 20 . In dem Term<br />
p 2 r<br />
2m<br />
pr = ¯h 1 ∂<br />
r (158)<br />
i r ∂r<br />
= − ¯h2<br />
2m<br />
1<br />
r<br />
∂ 2<br />
r<br />
∂r2 erkennen wir nun in <strong>der</strong> Tat den ersten Term von Gl. (147). Durch Vergleich des<br />
zweiten Terms folgern wir dann<br />
L 2 = −¯h 2<br />
<br />
∂<br />
∂µ (1 − µ2 ) ∂ 1<br />
+<br />
∂µ 1 − µ 2<br />
∂2 ∂ϕ2 <br />
, (159)<br />
ein Ergebnis, das man auch direkt aus Gl. (157) durch Einführung von Polarkoordinaten<br />
<strong>und</strong> Ausmultiplizieren (siehe Schiff S. 74/75) erhalten kann. Die Kugelflächenfunktionen<br />
Ylm sind also Eigenfunktionen des Drehimpuls–Quadrats [vgl.<br />
Gln. (150, 154)]:<br />
L 2 Ylm(ϑ, ϕ) = l(l + 1)¯h 2 Ylm(ϑ, ϕ). (160)<br />
Um die Eigenwerte l(l +1)¯h 2 besser zu verstehen, gehen wir nun vom Drehimpuls<br />
L selbst aus <strong>und</strong> betrachten seine z–Komponente<br />
Lz = xpy − ypx = ¯h<br />
i<br />
Führen wir nun ebene Polarkoordinaten<br />
x = ρ cos ϕ =⇒ ∂x<br />
∂ϕ<br />
y = ρ sin ϕ =⇒ ∂y<br />
∂ϕ<br />
<br />
x ∂<br />
<br />
∂<br />
− y .<br />
∂y ∂x<br />
= −ρ sin ϕ = −y<br />
= ρ cos ϕ = x<br />
20 Messiah (Bd. I, Abschn. 9.1.1, Fußnote 2) weist darauf hin, daß pr hermitesch ist, aber<br />
aufgr<strong>und</strong> Normierungsschwierigkeiten keine Observable repräsentiert. Wir schließen uns diesem<br />
formalen Argument nicht an, da auch <strong>der</strong> kartesische Impuls entsprechende Schwierigkeiten mit<br />
sich bringt (vgl. Übungen SS 2006, Blatt 6, Aufg. 2).<br />
63
ein, so folgt<br />
Lz = ¯h<br />
i<br />
Beim Eigenwertproblem von Lz<br />
∂y<br />
∂ϕ<br />
∂ ∂x<br />
+<br />
∂y ∂ϕ<br />
LzΦ = ¯h ∂Φ<br />
i ∂ϕ<br />
<br />
∂<br />
∂x<br />
= m¯hΦ<br />
= ¯h<br />
i<br />
werden wir nun genau auf die Separationslösungen (153)<br />
Φm(ϕ) = e imϕ<br />
(m = 0, ±1, ±2 . . .)<br />
∂<br />
. (161)<br />
∂ϕ<br />
geführt. Die Kugelflächenfunktionen Ylm sind also auch Eigenfunktionen <strong>der</strong> z–<br />
Komponente Lz des Drehimpulses:<br />
LzYlm(ϑ, ϕ) = m¯hYlm(ϑ, ϕ). (162)<br />
L 2 <strong>und</strong> Lz besitzen also ein gemeinsames System von Eigenfunktionen. In diesen<br />
Eigenfunktionen tritt <strong>der</strong> Drehimpuls Lz gequantelt in Vielfachen von ¯h auf. Dabei<br />
ist zu beachten, daß diese Quantelung <strong>für</strong> jede beliebige Richtung <strong>der</strong> z–Achse gilt.<br />
Wir können uns L also nicht mehr als festen “Pfeil” <strong>der</strong> Länge L, <strong>und</strong> Lz nicht<br />
mehr als seine Projektion L cos ϑ vorstellen.<br />
In <strong>der</strong> klassischen Mechanik hatten wir die z–Achse in die Richtung des konstanten<br />
Drehimpulses gelegt, d. h. wir hatten Lx = 0, Ly = 0, Lz = L. Wenn wir<br />
dieses Konzept so gut wie möglich zu übernehmen versuchen, gehen wir von<br />
〈Lz〉 = l¯h (163)<br />
aus. Die entsprechende klassische Festlegung Lx = Ly = 0 können wir nun<br />
aber nicht erfüllen, denn zwischen den Drehimpulskomponenten besteht eine<br />
Unschärferelation [vgl. Gl. (81)]<br />
〈L 2 x〉〈L 2 y〉 ≥ ¯h2<br />
4 〈Lz〉 2 .<br />
Nehmen wir nun aus Symmetriegründen 〈L2 x 〉 = 〈L2y 〉 an <strong>und</strong> rechnen mit <strong>der</strong><br />
minimalen Unschärfe, so folgt<br />
〈L 2 x = 〈L 2 y〉 = ¯h<br />
2 〈Lz〉 = l<br />
2 ¯h2 .<br />
64
Damit erhalten wir <strong>für</strong> das Drehimpulsquadrat den Erwartungswert<br />
〈L 2 〉 = 〈L 2 x〉 + 〈L 2 y〉 + 〈L 2 z〉 = l¯h 2 + l 2 ¯h 2<br />
o<strong>der</strong><br />
〈L 2 〉 = l(l + 1)¯h 2 . (164)<br />
Das macht uns den Eigenwert l(l + 1)¯h 2 des Operators L 2 verständlich: In den<br />
Eigenfunktionen erscheint die z–Komponente des Drehimpulses in Vielfachen von<br />
¯h gequantelt. Versuchen wir, die z–Achse in die Richtung des Drehimpulses zu<br />
legen (Lz → l¯h), so können Lx <strong>und</strong> Ly aufgr<strong>und</strong> <strong>der</strong> Unschärferelation doch nicht<br />
exakt verschwinden. Die minimale Unschärfe führt dann dazu, daß L 2 nicht den<br />
Eigenwert l 2 ¯h 2 , son<strong>der</strong>n den größeren Eigenwert l(l + 1)¯h 2 erhält.<br />
Wählen wir bei festem L eine an<strong>der</strong>e Richtung als z–Achse, so werden wir bei<br />
einer Messung wie<strong>der</strong> nur gequantelte Werte m¯h <strong>für</strong> Lz finden. Hieraus wird die<br />
Einschränkung −l ≤ m ≤ l unmittelbar verständlich. Wir dürfen uns damit den<br />
Drehimpuls nicht mehr als Vektorpfeil, son<strong>der</strong>n als Kegelmantel veranschaulichen:<br />
mh<br />
z<br />
l(l+1)h<br />
Die (2l + 1) “Einstellmöglichkeiten” m = −l, . . . , m = +l des Drehimpulses bei<br />
festem L werden auch als “Richtungsquantelung” bezeichnet.<br />
Fassen wir also zusammen: Die Separationslösung <strong>der</strong> Schrödingergleichung hat<br />
uns auf Winkelfunktionen (Kugelflächenfunktionen) Ylm(ϑ, ϕ) geführt, die sich als<br />
Drehimpuls–Eigenfunktionen — genauer: als gemeinsame Eigenfunktionen <strong>der</strong><br />
Operatoren Lz (Eigenwert m¯h) <strong>und</strong> L 2 (Eigenwert l(l + 1)¯h 2 ) — herausstellen.<br />
Damit kommen wir nun zur radialen Gleichung (vgl. (149))<br />
− ¯h2<br />
2m<br />
d2 <br />
u<br />
+ V (r) +<br />
dr2 65<br />
l(l + 1)¯h2<br />
2mr2 <br />
u = Eu. (165)
Diese Gleichung können wir als eindimensionale Schrödingergleichung mit dem<br />
effektiven Potential<br />
˜V (r) = V (r) +<br />
l(l + 1)¯h2<br />
2mr 2<br />
interpretieren — in völliger Analogie zur klassischen Mechanik. Das Fliehkraftpotential<br />
l(l + 1)¯h 2 /2mr 2 hängt von <strong>der</strong> Quantenzahl l, die den Betrag des Drehimpulses<br />
angibt, nicht aber von <strong>der</strong> Quantenzahl m, die seine Richtung angibt,<br />
ab 21 . Dementsprechend sind alle Eigenwerte von Gl. (165) (2l + 1)– fach entartet.<br />
Hierin zeigt sich die Isotropie des Problems. Stört man diese Isotropie, indem<br />
man z. B. ein Magnetfeld anlegt, das eine Raumrichtung auszeichnet, wird diese<br />
Entartung aufgehoben. m heißt darum auch magnetische Quantenzahl.<br />
In allen praktisch interessanten Fällen dominiert das Fliehkraftpotential <strong>für</strong> l = 0<br />
<strong>und</strong> r → 0 gegenüber V (r):<br />
V<br />
∼<br />
V(r)<br />
V(r)<br />
Das resultierende Minimum des Potentials ermöglicht klassische Bahnen, die den<br />
Planetenbahnen entsprechen. Solche klassischen Bahnen sind natürlich <strong>für</strong> alle<br />
E < 0 möglich. Quantenmechanisch finden wir dagegen nur <strong>für</strong> bestimmte Energien<br />
Eνl stationäre Zustände. Das ergibt sich in Analogie zum eindimensionalen<br />
Fall aus folgen<strong>der</strong> Überlegung:<br />
Da das Fliehkraftpotential <strong>für</strong> kleine Abstände dominiert, erhalten wir <strong>für</strong> r → 0<br />
die Differentialgleichung<br />
mit <strong>der</strong> allgemeinen Lösung<br />
u ′′ =<br />
l(l + 1)<br />
r2 u<br />
21 Man vermeide Verwechselungen <strong>der</strong> Masse m <strong>und</strong> <strong>der</strong> Quantenzahl m!<br />
66<br />
r
u → alr l+1 + Alr −l<br />
Für r → ∞ dominiert dagegen <strong>der</strong> Term Eu <strong>und</strong> wir haben<br />
also<br />
Die Normierung 22<br />
<br />
u ′′ = κ 2 u mit κ 2 = − 2mE<br />
¯h 2<br />
u → ble −κr + Ble +κr<br />
χ 2 d 3 ∞<br />
r = 4π<br />
0<br />
u<br />
r<br />
2<br />
r 2 dr = 4π<br />
(r → 0). (166)<br />
> 0,<br />
(r → ∞). (167)<br />
∞<br />
0<br />
u 2 dr = 1 (168)<br />
verlangt nun, daß Al <strong>und</strong> Bl verschwinden. Diese Konstanten sind aber nicht<br />
unabhängig wählbar. Starte ich z. B. eine numerische Integration mit al = 0 <strong>und</strong><br />
Al = 0, so werden sich bl <strong>und</strong> Bl aus <strong>der</strong> Rechnung ergeben. Nur <strong>für</strong> bestimmte<br />
Werte Enl <strong>der</strong> Energie wird dabei Bl = 0 werden. Wir erwarten also radiale<br />
Eigenfunktionen unl(r), die von zwei diskreten Quantenzahlen l <strong>und</strong> n abhängen.<br />
Insgesamt sind die stationären Wellenfunktionen<br />
χnlm(r, ϑ, ϕ) = 1<br />
r unl(r)Ylm(ϑ, ϕ)<br />
des Separationsansatzes (148) also durch die drei Quantenzahlen n, l <strong>und</strong> m charakterisiert.<br />
Diese Anzahl ist auch aus den drei Raumrichtungen zu erwarten.<br />
3.7 Das Wasserstoffatom<br />
Als spezielles Beispiel eines kugelsymmetrischen Potentials betrachten wir nun<br />
das Coulombpotential<br />
V (r) = − e2<br />
4πε0r<br />
22 Beachte, daß damit nicht χ, son<strong>der</strong>n u = χr <strong>der</strong> eindimensionalen Wellenfunktion entspricht.<br />
Damit wird die Interpretation von Gl. (165) als eindimensionale Schrödingergleichung<br />
perfekt.<br />
67
<strong>und</strong> kommen damit zur Theorie des Elektronenzustandes im Wasserstoffatom 23 .<br />
Zur bequemen Rechnung machen wir die Schrödingergleichung [vgl. Gl. (165)]<br />
durch<br />
mit dem Bohrschen Radius<br />
<strong>und</strong> <strong>der</strong> Rydberg–Energie<br />
d2 <br />
u 2m me2<br />
+<br />
dr2 2 E +<br />
¯h 4πε0¯h 2<br />
2 l(l + 1)<br />
−<br />
r r2 <br />
u = 0<br />
r = a0x <strong>und</strong> E = −Rκ 2<br />
a0 =<br />
R = ¯h2<br />
2ma 2 0<br />
dimensionslos <strong>und</strong> erhalten<br />
(169)<br />
4πε0¯h 2<br />
me 2 = 5.29 · 10−11 m (170)<br />
= 1<br />
2 mc2<br />
<br />
2 2<br />
e<br />
= 13.6 eV (171)<br />
4πε0¯hc<br />
d2 <br />
u 2<br />
+<br />
dx2 x − κ2 −<br />
l(l + 1)<br />
x2 <br />
u = 0. (172)<br />
Nun wissen wir bereits aus <strong>der</strong> allgemeinen Diskussion, daß u <strong>für</strong> kleine x wie<br />
x l+1 , <strong>für</strong> große x wie e −κx gehen muß. Die spezielle Struktur von Gl. (172) legt es<br />
nun nahe, direkt durch den Produktansatz<br />
u = x l+1 e −κx<br />
nach den einfachsten Eigenfunktionen zu suchen. Bilden wir nämlich<br />
u ′′ = <br />
x l+1 ′′<br />
e −κx + 2 <br />
x l+1 ′ <br />
e −κx′ ′ <br />
l+1<br />
+ x e −κx ′′<br />
= l(l + 1)<br />
x2 u −<br />
2(l + 1)<br />
κu + κ<br />
x<br />
2 u,<br />
(173)<br />
so heben sich die Terme mit l(l + 1)/x 2 <strong>und</strong> mit κ 2 in Gl. (172) sofort weg. Durch<br />
die spezielle Wahl (l+1)κ = 1 bilanziert sich aber auch <strong>der</strong> 2/x–Term. Wir finden<br />
mit dem Ansatz (173) also tatsächlich Eigenfunktionen zu den Eigenwerten<br />
23 Wir vernachlässigen das Massenverhältnis m/mp <strong>und</strong> betrachten den Kern als ortsfest bei<br />
r = 0.<br />
68
κl1 = 1<br />
l + 1<br />
o<strong>der</strong> El1 = − R<br />
. (174)<br />
(l + 1) 2<br />
Nun existiert zu gegebenem l aber nicht nur ein Eigenwert κl1. Man kann durch<br />
den Ansatz<br />
u = ϱx l+1 e −κx<br />
systematisch nach weiteren Eigenfunktionen suchen <strong>und</strong> findet <strong>für</strong> bestimmte κlν<br />
Polynome ϱlν (Laguerresche Polynome) (ν − 1)–ten Grades. Diese Polynome werden<br />
aber zunehmend komplizierter <strong>und</strong> sollen hier nicht mehr untersucht werden.<br />
Wir notieren nur noch das Ergebnis<br />
κlν = 1<br />
l + ν<br />
o<strong>der</strong> Elν = − R<br />
(l + ν) 2<br />
mit ν = 1, 2, 3, . . .<br />
<strong>für</strong> sämtliche Energie–Eigenwerte Elν zu gegebenem Drehimpuls l. Alle Eigenwerte<br />
sind also von <strong>der</strong> Form<br />
κn = 1<br />
n o<strong>der</strong> En = − R<br />
, (175)<br />
n2 wobei n eine natürliche Zahl ist. Es ist üblich, von Gl. (175) auszugehen <strong>und</strong><br />
n als Hauptquantenzahl zu bezeichnen. Läßt man dann n die Werte 1, 2, 3, . . .<br />
durchlaufen, so trägt man <strong>der</strong> Bedingung n = l + ν (l = 0, 1, 2, . . . <strong>und</strong> ν =<br />
1, 2, 3, . . .) durch die Bedingung<br />
l = 0, 1, . . . , n − 1<br />
Rechnung. Zu je<strong>der</strong> Hauptquantenzahl n gibt es also n Drehimpulsquantenzahlen<br />
l. Berücksichtigt man weiter, daß zu jedem l die (2l + 1) magnetischen Quantenzahlen<br />
m = −l, −l + 1, . . . , l − 1, l<br />
gehören, so findet man, daß <strong>der</strong> Eigenwert En<br />
n−1 <br />
l=0<br />
(2l + 1) = n<br />
1 + [2(n−1)+1]<br />
2<br />
= n 2<br />
(176)<br />
–fach entartet ist. In <strong>der</strong> Atomphysik ist es (aus historischen Gründen) üblich, den<br />
Wert <strong>der</strong> Drehimpulsquantenzahl durch kleine lateinische Buchstaben s, p, d, f, . . .<br />
zu kennzeichnen <strong>und</strong> hinter die Hauptquantenzahl zu stellen. Damit ergibt sich<br />
das folgende Termschema des Wasserstoffs:<br />
69
Termschema des Wasserstoffs<br />
Nach dieser allgemeinen Übersicht kehren wir zu den speziellen Eigenfunktionen<br />
(173) zurück. Wenn wir von <strong>der</strong> Hauptquantenzahl n — also von einer vorgegebenen<br />
Energie — ausgehen, repräsentieren diese Eigenfunktionen die Zustände mit<br />
maximalen Drehimpuls l = n−1. Die klassische Entsprechung dieser Zustände<br />
sind Kreisbahnen mit<br />
pr = 0 <strong>und</strong> T = L2<br />
.<br />
2mr2 Wir wollen das durch eine kleine Rechnung bestätigen <strong>und</strong> schreiben Gl. (173)<br />
wegen l = n−1 in <strong>der</strong> Form<br />
Diese Eigenfunktionen haben ein Maximum bei<br />
ũn n−1 = x n x<br />
−<br />
e n . (177)<br />
xn = n 2 bzw. rn = n 2 a0 (178)<br />
<strong>und</strong> repräsentieren Wahrscheinlichkeitsdichten wn ∼ ũ2 n n−1 , die sich mit wachsendem<br />
n immer enger um xn bzw. rn konzentrieren. In <strong>der</strong> folgenden Figur zeigen<br />
wir das <strong>für</strong> die relativen Wahrscheinlichkeiten wn rel(x) = wn(x)/wn(xn):<br />
70
Relative radiale Wahrscheinlichkeitsverteilungen<br />
22<br />
wn rel(x) = ũ2 n n−1 (x)<br />
ũ 2 n n−1 (xn)<br />
des Wasserstoff–Elektrons in den<br />
Zuständen unl mit maximalem Drehimpuls<br />
l = n−1. (x = r/a0, xn = n 2 ).<br />
Wir können diese Aussage präzisieren, indem wir von <strong>der</strong> Formel<br />
∞<br />
0<br />
x m e −αx dx = 1<br />
α m+1<br />
∞<br />
0<br />
y m e −y dy = m!<br />
α m+1<br />
ausgehen <strong>und</strong> (mit <strong>der</strong> Abkürzung ũ = ũn n−1) die Normierung<br />
sowie die Momente<br />
〈ũ|ũ〉 =<br />
〈ũ|x k |ũ〉 =<br />
∞<br />
0<br />
∞<br />
0<br />
x 2n e<br />
x 2n+k e<br />
− 2<br />
− 2<br />
n x dx =<br />
n x dx =<br />
berechnen. Daraus folgen die Erwartungswerte 24<br />
Speziell <strong>für</strong> k = 1 erhalten wir<br />
〈x k 〉 = 〈ũ|xk |ũ〉<br />
〈ũ|ũ〉 =<br />
<br />
〈x〉 = n n + 1<br />
<br />
2<br />
<br />
n 2n+1<br />
(2n)!<br />
2<br />
<br />
n 2n+k+1<br />
(2n + k)!<br />
2<br />
<br />
n k (2n + k)!<br />
. (179)<br />
2 (2n)!<br />
<br />
o<strong>der</strong> 〈r〉 = n<br />
n + 1<br />
2<br />
<br />
a0,<br />
also einen “mittleren” Radius, <strong>der</strong> knapp über dem Maximum xn = n 2 bzw.<br />
rn = n 2 a0 (vgl. (178) liegt. Aus dem quadratischen Mittel<br />
24 Vgl. Gl. (168) <strong>und</strong> die Fußnote 20. Man beachte, daß in <strong>der</strong> Definition <strong>der</strong> radialen Wahrscheinlichkeit<br />
bereits die Kugeloberfläche berücksictigt ist.<br />
71
erechnen wir<br />
Die Streuung<br />
〈x 2 〉 = n 2 <br />
(n + 1) n + 1<br />
<br />
2<br />
∆x 2 = 〈x 2 〉 − 〈x〉 2 = n 2<br />
<br />
∆r<br />
〈r〉<br />
= ∆x<br />
〈x〉 =<br />
n + 1<br />
<br />
1 〈x〉2<br />
=<br />
2 2 2n + 1 .<br />
1<br />
√ 2n + 1<br />
fällt also mit wachsen<strong>der</strong> Quantenzahl n. Für sehr große n (große Energie) wird<br />
man das Elektron daher nur in <strong>der</strong> engsten Nachbarschaft einer Kugelschale von<br />
Radius rn = n 2 a0 antreffen. Daß es sich darüber hinaus um die engste Nachbarschaft<br />
von Kreisbahnen handelt, erkennt man erst an den zugehörigen Kugelfunktionen<br />
Ylm(ϑ, ϕ). Wenn wir — <strong>für</strong> große n <strong>und</strong> damit <strong>für</strong> große l = n − 1 — die<br />
Polarachse unseres Koordinatensystems “so gut wie möglich” in Drehimpulsrichtung<br />
legen wollen, müssen wir l = m wählen <strong>und</strong> finden tatsächlich Winkelanteile<br />
Yll ∼ sin l ϑ<br />
<strong>der</strong> Eigenfunktion, die die Konzentration um einen Kreisring in <strong>der</strong> Äquatorialebene<br />
bestätigen. An<strong>der</strong>e magnetische Quantenzahlen m beschreiben lediglich<br />
an<strong>der</strong>e Orientierungen <strong>der</strong> Polarachse.<br />
Wir folgern weiter (ohne das explizit zu beweisen), daß kleinere Drehimpulse<br />
l < n − 1 schließlich den Elipsenbahnen des Keplerproblems entsprechen.<br />
Kein klassisches Analogon besitzt <strong>der</strong> Gr<strong>und</strong>zustand<br />
u1 0(r) ∼ re −r/a0 bzw. χ1 0 0(r) ∼ e −r/a0 (180)<br />
des Elektrons im Wasserstoffatom mit <strong>der</strong> “Nullpunktsenergie” E1 = −R =<br />
−13.6 eV. Er entspricht einem Elektron ohne Drehimpuls, das sich aufgr<strong>und</strong> <strong>der</strong><br />
Coulombattraktion im Kern aufhalten “möchte”, daran aber durch die Orts–<br />
Impuls–Unschärfe gehin<strong>der</strong>t wird. Tatsächlich wird die Wahrscheinlichkeitsdichte<br />
w1(r) ∼ χ 2 1 0 0 = e −2r/a0<br />
am Kernort r = 0 am größten. Der Gr<strong>und</strong>zustand des Wasserstoffatoms entspricht<br />
also ganz dem klassisch ebenfalls nicht verständlichen Gr<strong>und</strong>zustand des<br />
harmonischen Oszillators.<br />
72
Wir schließen die Behandlung des Wasserstoffatoms mit einem neuen Gesichtspunkt<br />
zur korrekten Interpretation <strong>der</strong> Wellenfunktionen. Es liegt ja so nahe (wie<br />
das in vielen Büchern durch Abbildungen implizit suggeriert wird), ψ ∗ ψ bzw.<br />
χ ∗ χ als Dichteverteilung eines ausgeschmierten Elektrons zu interpretieren. Diese<br />
Interpretation hat darüber hinaus zunächst den Vorteil, daß sie erklärt, warum<br />
stationäre Zustände nicht strahlen. Nimmt man diese Interpretation aber ernst,so<br />
muß man im Potential die Raumladungsdichte ϱe = −e|χ| 2 berücksichtigen <strong>und</strong><br />
erhält<br />
Die stationäre Schrödingergleichung<br />
V (r) = − e2<br />
′ 2<br />
e2 |χ(r )|<br />
+<br />
4πε0r 4π |r − r ′ | d3r ′ .<br />
¯h 2<br />
′ 2<br />
e2 |χ(r )|<br />
∆χ +<br />
2m 4πε0 |r − r ′ | d3r − 1<br />
<br />
χ = Eχ<br />
r<br />
wird damit eine sehr verwickelte nicht–lineare Integro–Differentialgleichung. Sie<br />
ist aber nicht nur schwierig zu lösen, son<strong>der</strong>n nach Ausweis <strong>der</strong> Erfahrung falsch!<br />
Der Term<br />
e 2<br />
4πε0<br />
|χ(r ′ )| 2<br />
|r − r ′ | d3 r,<br />
<strong>der</strong> eine “Selbst–Wechselwirkung” des Elektrons darstellt, würde eine innere elektrostatische<br />
Abstoßung <strong>der</strong> ausgeschmierten “Elektronenwolke” bewirken, die we<strong>der</strong><br />
im Wasserstoffatom noch in irgendeinem an<strong>der</strong>en Experiment beobachtet<br />
wird. Wir hüten uns also davor, das Elektron im Wasserstoffatom (<strong>und</strong> an<strong>der</strong>swo)<br />
als Ladungswolke mit einer charakteristischen Ausdehnung a0 zu beschreiben.<br />
73
4 Mehrteilchensysteme<br />
4.1 Die Schrödingergleichung<br />
Wir haben bisher nur die <strong>Quantenmechanik</strong> eines Teilchens mit einer Hamiltonfunktion<br />
H(r1, p1) betrachtet. Diesem Teilchen hatten wir eine Wellenfunktion<br />
|1〉 = ψ(r1, t)<br />
zugeordnet, <strong>der</strong>en Absolutquadrat ψ ∗ ψ die Wahrscheinlichkeitsdichte angab, das<br />
Teilchen 1 am Ort r1 zu finden. ψ genügte <strong>der</strong> Schrödingergleichung<br />
H(r1, p1)ψ = i¯h ∂ψ<br />
∂t ,<br />
wobei H den Hamiltonoperator bezeichnet, <strong>der</strong> aus <strong>der</strong> Hamiltonfunktion hervorgeht,<br />
indem <strong>der</strong> Impuls durch den Impulsoperator<br />
ersetzt wird.<br />
p1 = ¯h<br />
i ∇1 = ¯h<br />
i<br />
Es liegt nahe <strong>und</strong> hat sich bewährt, dieses Konzept wie folgt auf Systeme von n<br />
Teilchen zu übertragen:<br />
Wir führen eine Wellenfunktion<br />
d<br />
dr1<br />
|1, . . . , n〉 = ψ(r1, . . . , rn, t) (181)<br />
ein, <strong>der</strong>en Absolutquadrat ψ ∗ ψ die Wahrscheinlichkeitsdichte angibt, Teilchen 1<br />
bei r1, Teilchen 2 bei r2, . . . <strong>und</strong> Teilchen n bei rn zu finden. Das heißt genauer:<br />
dW = |ψ(r1, . . . , rn, t)| 2 d 3 r1 . . . d 3 rn<br />
(182)<br />
ist die Wahrscheinlichkeit, das System <strong>der</strong> Teilchen 1, . . . , n im Volumenelement<br />
d 3 r1 . . . d 3 rn des 3n–dimensionalen Konfigurationsraums anzutreffen.<br />
Aus <strong>der</strong> klassischen Hamiltonfunktion<br />
H(r1, . . . , rn, p1, . . . , pn) =<br />
n<br />
ν=1<br />
p 2 ν<br />
2mν<br />
+ V (r1, . . . , rn) (183)<br />
bilden wir den Hamiltonoperator H, indem wir die Impulse durch die Impulsoperatoren<br />
74
pν = ¯h<br />
i ∇ν = ¯h<br />
i<br />
ersetzen. Dann genügt die Wellenfunktion <strong>der</strong> Schrödingergleichung<br />
o<strong>der</strong> explizit<br />
i¯h ∂ψ<br />
∂t<br />
d<br />
drν<br />
(184)<br />
i¯h ∂<br />
|1, . . . n〉 = H|1, . . . , n〉, (185)<br />
∂t<br />
= −<br />
n ¯h 2<br />
∆νψ + V (r1, . . . , rn)ψ. (186)<br />
2mν<br />
ν=1<br />
Wie bisher können wir durch den Separationsansatz<br />
E<br />
−i<br />
ψ(r1, . . . , rn, t) = ϕ(r1, . . . , rn)e ¯h t<br />
(187)<br />
zu stationären Zuständen ϕ übergehen, die <strong>der</strong> stationären Schrödingergleichung<br />
−<br />
n ¯h 2<br />
∆νϕ + V (r1, . . . , rn)ϕ = Eϕ. (188)<br />
2mν<br />
ν=1<br />
genügen. Im Gegensatz zum Einteilchenproblem wollen wir dieses Konzept aber<br />
nicht mehr durch explizite Lösungsbeispiele illustrieren, da schon das klassische<br />
Mehrteilchenproblem nicht mehr analytisch lösbar ist 25 . Stattdessen wollen wir<br />
einige prinzipielle Aspekte ansprechen, die kein klassisches Analogon besitzen <strong>und</strong><br />
<strong>für</strong> die Atomphysik bedeutsam sind.<br />
4.2 Identische Teilchen <strong>und</strong> Spin<br />
Wir betrachten zwei identische Teilchen 1,2 mit dem symmetrischen Hamiltonoperator<br />
H = 1<br />
2m (p2 1 + p2 2 ) + V (r1) + V (r2) + U(|r1 − r2|). (189)<br />
Eine Lösung <strong>der</strong> Schrödingergleichung, die etwa aus <strong>der</strong> Anfangsbedingung<br />
ψ12(t = 0) = ψa(r1, 0)ψb(r2, 0)<br />
25 Eine Separation in Relativ– <strong>und</strong> Schwerpunktskoordinaten ist auch quantenmechanisch<br />
möglich. Dementspreched ist auch das quantenmechanische Zweiteilchenproblem ohne äußere<br />
Kräfte auf das Einteilchenproblem zurückzuführen.<br />
75
(unkorrelierte Anfangszustände) hervorgehe, sei<br />
ψ12 = ψab(r1, r2, t).<br />
Wollen wir |ψ12| 2 nach Gl.(182) als Wahrscheinlichkeitsdichte interpretieren, so<br />
müssen wir uns fragen, wie wir die Teilchen 1 <strong>und</strong> 2 unterscheiden wollen. Denn<br />
die <strong>Quantenmechanik</strong> beschreibt nicht die Dinge an sich, son<strong>der</strong>n unsere Beobachtung.<br />
In <strong>der</strong> klassischen Physik ist dies kein Problem, denn wir können die<br />
Teilchen einfach unterscheiden, indem wir<br />
a) die Teilchen durch Marken (z. B. Farbe, Zeichen), welche die Dynamik nicht<br />
beeinflussen, kennzeichnen o<strong>der</strong><br />
b) die Teilchen identifizieren, indem wir ihre Bahn verfolgen.<br />
Für identische mikroskopische Objekte kennen wir keine Marken, die eine solche<br />
Kennzeichnung erlauben. In <strong>der</strong> <strong>Quantenmechanik</strong> gibt es auch keine wohldefinierten<br />
Bahnen, die wir verfolgen können, insbeson<strong>der</strong>e dann nicht, wenn sich<br />
die Wellenfunktionen <strong>der</strong> Teilchen überlappen. Wir können die Wahrscheinlichkeit,<br />
am Ort r1 Teilchen 1 <strong>und</strong> am Ort r2 Teilchen 2 anzutreffen also gar nicht<br />
im Experiment überprüfen, da die Unterscheidung <strong>der</strong> Teilchen 1 <strong>und</strong> 2 nicht <strong>der</strong><br />
Beobachtung zugänglich ist: Wir können nur die Wahrscheinlichkeit angeben, daß<br />
sowohl bei r1 als auch bei r2 ein Teilchendetektor anspricht.<br />
Da also die <strong>Quantenmechanik</strong> gr<strong>und</strong>sätzlich nur die (potentielle) Beobachtung<br />
beschreibt, müssen wir neben ψ12 auch<br />
ψ21 = ψab(r2, r1, t)<br />
als gleichberechtigte Wellenfunktion zulassen. Aus <strong>der</strong> Symmetrie von H folgt,<br />
daß ψ21 auch <strong>der</strong> selben Schrödingergleichung genügt 26 .<br />
Darüber hinaus müssen wir dann auch Linearkombinationen<br />
ψ(r1, r2, t) = αψ12 + βψ21<br />
in Betracht ziehen. Verlangen wir nun, daß sich die Wahrscheinlichkeitsdichte ψ ∗ ψ<br />
bei einer Vertauschung nicht än<strong>der</strong>t, so folgt<br />
also<br />
|ψ(r1, r2, t)| 2 = |ψ(r2, r1, t)| 2 ,<br />
ψ(r1, r2, t) = cψ(r2, r1, t)<br />
26 Entsprechend existieren auch alle Eigenfunktionen doppelt: Man spricht von Austauschent-<br />
artung.<br />
76
mit c ∗ c = 1. Bei zwei Vertauschungen än<strong>der</strong>t sich natürlich gar nichts, also gilt<br />
c 2 = 1 o<strong>der</strong> c = ±1. Den beiden möglichen Vorzeichen entsprechen die beiden<br />
einzigen Möglichkeiten<br />
ψsym ∼ ψ12 + ψ21 <strong>und</strong><br />
ψasy ∼ ψ12 − ψ21. (190)<br />
Wellenfunktionen identischer Teilchen sind also entwe<strong>der</strong> symmetrisch o<strong>der</strong> antisymmetrisch.<br />
An dieser Stelle müssen wir auf den Spin eines Teilchens zu sprechen kommen,<br />
den die relativistische Diracgleichung postuliert <strong>und</strong> <strong>der</strong> beispielsweise durch<br />
ein Magnetfeld beobachtbar ist. Der Spin s ist eine vektorielle Observable ohne<br />
klassisches Analogon, die quantenmechanisch den selben Rechenregeln folgt wie<br />
Drehimpulse 27 (Übungen). Auch <strong>der</strong> Spin ist gequantelt, kann im Gegensatz zu<br />
Bahndrehimpulsen aber nicht nur ganzzahlige, son<strong>der</strong>n auch halbzahlige Vielfache<br />
von ¯h annehmen.<br />
Es hat sich nun als wichtig erwiesen, zwei Gruppen von Teilchen gr<strong>und</strong>sätzlich<br />
zu unterscheiden, nämlich<br />
• Fermionen mit halbzahligem Spin <strong>und</strong><br />
• Bosonen mit ganzzahligem Spin.<br />
Zu den Fermionen zählen insbeson<strong>der</strong>e Elektronen, Protonen, Neutronen (Spin<br />
1)<br />
sowie alle Atomkerne, Atome <strong>und</strong> Moleküle, die aus einer ungeraden Anzahl<br />
2<br />
(z. B. He3) elementarer Fermionen zusammengesetzt sind.<br />
Dagegen gehören bestimmte Elementarteilchen wie Pionen <strong>und</strong> Photonen sowie<br />
alle zusammengesetzten Teilchen mit gera<strong>der</strong> Fermionenanzahl (z. B. He4) zu den<br />
Bosonen.<br />
Für spinbehaftete Teilchen stellt die Richtung von s nun eine Observable dar, die<br />
in <strong>der</strong> ψ–Funktion durch eine zusätzliche (diskrete) Variable berücksichtigt werden<br />
muß. Statt ψ(r1, r2, t) müssen wir also Zustandsfunktionen ˆ ψ(r1, s1, r2, s2, t)<br />
betrachten. Für die so komplettierten Wellenfunktionen gilt nun nach Ausweis<br />
<strong>der</strong> Erfahrung<br />
• Fermionen werden durch antisymmetrische Wellenfunktionen ˆ ψ <strong>und</strong><br />
27 Man stellt sich den Spin daher auch gern als inneren Drehimpuls durch eine Rotation<br />
des Teilchens vor. Diese Vorstellung kann allerdings das Wesen des Spins nicht erfassen (siehe<br />
Übungen).<br />
77
• Bosonen werden durch symmetrische Wellenfunktionen ˆ ψ beschrieben.<br />
Läßt man den Spin in <strong>der</strong> Anschrift <strong>der</strong> ψ–Funktion weg, muß man Fallunterscheidungen<br />
je nach Ausrichtung <strong>der</strong> Spins treffen. Insbeson<strong>der</strong>e gilt <strong>für</strong> die “elementaren”<br />
Fermionen mit Spin 1<br />
2 :<br />
–Teilchen mit paralellem Spin haben antisymmetrische <strong>und</strong> Spin 1<br />
2 –Teilchen<br />
Spin 1<br />
2<br />
mit antiparalellem Spin haben symmetrische Wellenfunktionen ψ.<br />
Aus <strong>der</strong> (Anti–)Symmetrie ergibt sich <strong>für</strong> Fermionen eine Folgerung großer Tragweite:<br />
Haben zwei gleiche Fermionen den selben Spin s <strong>und</strong> werden sie durch die<br />
selbe Wellenfunktion ψ0 beschrieben, so wird<br />
ψ(r1, r2, t) = ψ0(r1, t)ψ0(r2, t) − ψ0(r2, t)ψ0(r1, t) = 0.<br />
Für die stationären Zustände folgt daraus das Pauli–Prinzip<br />
• Zwei gleiche Fermionen können nicht in allen Quantenzahlen übereinstimmen<br />
<strong>und</strong> den selben Spin haben.<br />
An<strong>der</strong>s ausgedrückt: Charakterisieren wir die stationären Zustände, die ein Fermion<br />
annehmen kann, durch einen Satz von Quantenzahlen (etwa n, l, m <strong>und</strong><br />
sz), so können diese Zustände nur die Besetzungszahlen 0 o<strong>der</strong> 1 aufweisen.<br />
Ein analoges Prinzip <strong>für</strong> Bosonen gibt es nicht, Bosonenzustände können beliebige<br />
Besetzungszahlen 0, 1, 2, . . . annehmen.<br />
4.3 Atombau <strong>und</strong> periodisches System <strong>der</strong> Elemente<br />
Wir betrachten nun Atomkerne höherer Ladungszahl, die zur Neutralisation mehrere<br />
Hüllenelektronen benötigen. Um ein Ordnungsschema in dieses komplexe<br />
Problem zu bringen, denken wir uns solche Atome (im Gr<strong>und</strong>zustand) schrittweise<br />
aufgebaut: Wir denken uns k − 1 Elektronen bereits mehr o<strong>der</strong> weniger kugelsymmetrisch<br />
um den Kern verteilt <strong>und</strong> fragen nach den möglichen Zuständen des<br />
k–ten Elektrons. Damit können wir an die generelle Diskussion des kugelsymmetrischen<br />
Potentials (Abschnitt 3.5) anknüpfen <strong>und</strong> führen die Quantenzahlen n, l<br />
<strong>und</strong> m ein. Außerdem müssen wir <strong>für</strong> die Elektronen mit dem Spin 1 noch die<br />
2<br />
beiden Spinrichtungen sz = 1<br />
2 <strong>und</strong> sz = − 1<br />
unterscheiden (Richtungquantelung<br />
2<br />
<strong>der</strong> Drehimpulse).<br />
Entsprechend <strong>der</strong> Hauptquantenzahl n denken wir uns die Atomelektronen in<br />
Schalen angeordnet. Innerhalb je<strong>der</strong> Schale stehen uns dann die Quantenzahlen<br />
l = 0, . . . , n − 1 , m = −l, . . . , l <strong>und</strong> sz = ± 1<br />
2<br />
78
zur Verfügung.<br />
Für die erste Schale n = 1 liegen l = 0 <strong>und</strong> m = 0 fest, es gibt also <strong>für</strong> n = 1<br />
genau zwei verschiedene Elektronenzustände mit sz = +1/2 <strong>und</strong> sz = −1/2.<br />
Da nach dem Pauliprinzip je<strong>der</strong> Zustand höchstens einfach besetzt ist, kann die<br />
erste Schale höchstens zwei Elektronen “aufnehmen”: Sie ist beim Element 2He<br />
abgeschlossen.<br />
Benötigen wir also mehr als zwei Elektronen, um die Kernladung zu kompensieren,<br />
müssen wir die zweite Schale auffüllen. Hier können (l, m) die Dupel (1,1),<br />
(1,0), (1,–1) <strong>und</strong> (0,0) annehmen. Mit den beiden Spinrichtungen gibt das 8 mögliche<br />
Zustände in <strong>der</strong> zweiten Schale, die nach dem Pauliprinzip wie<strong>der</strong> höchsten<br />
einfach besetzt werden können. Beim Element 10Ne ist neben <strong>der</strong> ersten also auch<br />
die zweite Schale abgeschlossen.<br />
Generell hatten wir beim Wasserstoff ausgerechnet, daß es zu je<strong>der</strong> Hauptquantenzahl<br />
n einen Satz von n 2 verschiedenen Nebenquantenzahlen gibt. Unter Berücksichtigung<br />
<strong>der</strong> beiden Spinrichtungen kann die n–te Schale also maximal 2n 2 Elektronen<br />
aufnehmen. Die dritte Schale kann demnach 18 Elektronen aufnehmen <strong>und</strong><br />
wäre beim Element 28Ni abgeschlossen.<br />
Tatsächlich bleibt aber nicht alles so schön wasserstoffähnlich, weil die Elektronen<br />
untereinan<strong>der</strong> wechselwirken. Dadurch wird nicht nur die Entartung des Wasserstoffs<br />
(Enl hängt hier nicht von l ab) aufgehoben, son<strong>der</strong>n es kann sogar<br />
Enl > En+1 0<br />
werden. Das Atom zieht es dann vor, eine “neue” Schale (n+1) zu beginnen, ehe<br />
die “alte” (n) abgeschlossen ist.<br />
Der Gr<strong>und</strong> hier<strong>für</strong> ist sogar aus <strong>der</strong> klassischen Mechanik verständlich: Bei niedrigem<br />
Drehimpuls hält sich das Elektron weitgehend in Kernnähe auf (vgl. den<br />
Gr<strong>und</strong>zustand des Wassestoffs) <strong>und</strong> “sieht” die übrigen Elektronen nicht. Elektronen<br />
mit großem l dagegen halten sich überwiegend in großer Entfernung (vgl.<br />
die “Kreisbahnen” beim Wasserstoff <strong>für</strong> l = n − 1) auf, wo <strong>der</strong> Kern durch die<br />
übrigen Elektronen weitgehend abgeschirmt ist.<br />
Darum werden in <strong>der</strong> Schale n = 3 zunächst nur die acht s– (l = 0) <strong>und</strong> p–<br />
Zustände (l = 1) aufgefüllt, <strong>und</strong> das ist beim Element 18Ar erreicht. Danach<br />
werden zunächst die beiden s–Zustände <strong>der</strong> vierten Schale besetzt (19K <strong>und</strong> 20Ca)<br />
<strong>und</strong> dann erst die zehn d–Zustände (l = 2) <strong>der</strong> dritten Schale aufgefüllt.<br />
Das Element 30Zn hat also eine voll besetzte dritte Schale <strong>und</strong> — wie 20Ca —<br />
zwei s–Elektronen in <strong>der</strong> vierten Schale. Bei 31Ga wird nun ein drittes Elektron<br />
in die vierte Schale aufgenommen, <strong>und</strong> bei 36Kr sind die energetisch günstigen<br />
s– <strong>und</strong> p–Zustände <strong>der</strong> vierten Schale besetzt. In ähnlicher Weise geht es weiter,<br />
79
die Details sind in <strong>der</strong> folgenden Tabelle zusammengefaßt, die angibt, in welchem<br />
Zustand das letzte (o<strong>der</strong> vorletzte 28 ) Elektron eingebaut wird.<br />
1 2 3 4 5 6 7<br />
s 1H 2He 3Li 4Be 11Na 12Mg 19K 20Ca 37Rb 38Sr 55Cs 56Ba 87Fr 88Ra<br />
5B 6C 13Al 14Si 31Ga 32Ge 49In 50Sn 81Tl 82Pb<br />
p 7N 8O 15P 16S 33As 34Se 51Sb 52Te 83Bi 84Po<br />
9F 10Ne 17Cl 18A 35Br 36Kr 53J 54Xe 85At 86Rn<br />
21Sc 22Ti 39Y 40Zr 57La 72Hf 89Ac 104<br />
23V 24Cr 41Nb 42Mo 73Ta 74W . . .<br />
d 25Mn 26Fe 43Tc 44Ru 75Re 76Os<br />
27Co 28Ni 45Rh 46Pd 77Ir 78Pt<br />
29Cu 30Zn 47Ag 48Cd 79Au 80Hg<br />
58Ce 59Pr 90Th 91Pa<br />
60Nd 61Pm 92U 93Np<br />
62Sm 63Eu 94Pu 95Am<br />
f 64Gd 65Tb 96Cm 97Bk<br />
66Dy 67Ho 98Cf 99E<br />
68Er 69Tm 100 101<br />
70Y 71Lu 102 103<br />
Da die chemischen Eigenschaften eines Elements wesentlich durch die Elektronen<br />
<strong>der</strong> äußersten Schale bestimmt sind, kommt man so zu einer gewissen Periodizität<br />
<strong>der</strong> chemischen Eigenschaften, z. B.:<br />
- Ist die äußerste Schale — o<strong>der</strong> ihre energetisch beson<strong>der</strong>s günstigen s– <strong>und</strong><br />
p–Zustände — gerade abgeschlossen, ist das Atom beson<strong>der</strong>s stabil, d. h.<br />
chemisch träge: Wir haben Edelgase (2He, 10Ne, 18A, 36Kr, . . . ).<br />
- Fehlen nur wenige Elektronen an einer solchen Edelgaskonfiguration, nimmt<br />
das Atom bei Reaktionen “gern” Elektronen auf (Halogene <strong>und</strong> Chalkogene).<br />
- Ist dagegen die äußerste Schale nur mit wenigen Elektronen besetzt, werden<br />
diese in Reaktionen leicht abgegeben (Alkali– <strong>und</strong> Erdalkali–Metalle).<br />
Die Quasi–Periodizität demonstriert man im Periodischen System <strong>der</strong> Elemente<br />
mit<br />
- Hauptgruppen, in denen nur s– <strong>und</strong> p–Zustände eine Rolle spielen<br />
- Nebengruppen, in denen die d–Zustände aufgefüllt werden <strong>und</strong><br />
- den Lanthanoiden <strong>und</strong> Aktinoiden, in denen schließlich die f–Zustände aufgefüllt<br />
werden.<br />
28 Bei konkurrierenden Zuständen kommt es gelegentlich zu kleinen Verschiebungen. Beispielsweise<br />
besitzen Cu, Ag <strong>und</strong> Au nur ein s–Elektron in <strong>der</strong> äußersten Schale, so daß bei Zn, Cd<br />
<strong>und</strong> Hg nicht ein d– son<strong>der</strong>n das fehlende s–Elektron eingebaut wird.<br />
80
4.4 Die Bildung von Molekülen<br />
Ein 17Cl–Atom hat gerade noch Platz <strong>für</strong> ein Elektron frei, um die energetisch<br />
günstige 18A–Konfiguration auszunutzen. Ein 19K–Atom dagegen hat <strong>für</strong> diese<br />
Konfiguration gerade ein Elektron zuviel <strong>und</strong> muß eine neue — energetisch viel<br />
ungünstigere — Schale “anbrechen”. Bringt man daher ein K– <strong>und</strong> ein Cl–Atom<br />
zusammen, so ist es energetisch günstig, wenn das K–Atom ein Elektron an das Cl<br />
abgibt. Freilich bleiben die Atome dabei nicht elektrisch neutral, son<strong>der</strong>n werden<br />
zu K + – <strong>und</strong> Cl − –Ionen. Aufgr<strong>und</strong> <strong>der</strong> elektrostatischen Anziehung werden diese<br />
Ionen also aneinan<strong>der</strong> “gekettet”: K <strong>und</strong> Cl gehen eine heteropolare o<strong>der</strong> Ionen–<br />
Bindung ein <strong>und</strong> bilden ein KCl–Molekül — o<strong>der</strong> genauer: Viele K + – <strong>und</strong> Cl − –<br />
Ionen bilden ein Ionengitter.<br />
Diese einfache Ionenbindung ist jedoch nicht <strong>der</strong> Regelfall. Schließen sich insbeson<strong>der</strong>e<br />
zwei gleiche Atome zu einem Molekül (Beispielsweise H2) zusammen, so<br />
erwarten wir schon aus Symmetriegründen keine elektrische Aufladung <strong>der</strong> beiden<br />
Reaktionspartner: Die Bindung ist nun homöopolar 29 (man spricht auch von<br />
Atombindung).<br />
Die homöopolare Bindung ist rein klassisch nicht zu verstehen <strong>und</strong> quantenmechanisch<br />
schwierig zu beschreiben. Wir begnügen uns daher mit einer skizzenhaften<br />
Erläuterung <strong>der</strong> Bildung des H2–Moleküls. Dazu betrachten wir zwei räumlich<br />
fixierte Wasserstoffkerne (A) <strong>und</strong> (B) im Abstand a <strong>und</strong> notieren den Hamiltonoperator<br />
H = − ¯h2<br />
2m (∆1 + ∆2) − e2<br />
4πε0<br />
1<br />
r1A<br />
+ 1<br />
r2B<br />
+ 1<br />
r1B<br />
+ 1<br />
−<br />
r2A<br />
1<br />
r12<br />
des Systems <strong>der</strong> beiden Elektronen (1) <strong>und</strong> (2) (siehe Skizze).<br />
r 1A<br />
1<br />
r 2A<br />
r 12<br />
r 1B<br />
A B<br />
a<br />
2<br />
r 2B<br />
− 1<br />
<br />
a<br />
(191)<br />
Bei hinreichend großem Abstand (a ≫ a0) <strong>der</strong> Kerne sind die vier letzten Terme<br />
zu vernachlässigen <strong>und</strong> H ist die Hamiltonfunktion zweier ungestörter H–Atome.<br />
Der Gr<strong>und</strong>zustand des Systems ist dann durch<br />
29 In <strong>der</strong> Chemie gibt es stufenlose Übergänge zwischen diesen Haupt–Bindungsarten.<br />
81
ϕ1(r1, r2) = χA(r1)χB(r2) (192)<br />
gegeben, wobei χA(r1) = χ1 0 0(r1A) <strong>und</strong> χB(r2) = χ1 0 0(r2B) den jeweiligen<br />
Gr<strong>und</strong>zustand <strong>der</strong> beiden Wasserstoffatome bezeichnen. Machen wir a kleiner,<br />
kommen die “Störglie<strong>der</strong>” allmählich ins Spiel. Dabei wird (192) aber zunächst<br />
noch eine brauchbare Näherung bleiben. Allerdings müssen wir wegen <strong>der</strong> Ununterscheidbarkeit<br />
<strong>der</strong> Elektronen <strong>und</strong> <strong>der</strong> Symmetrie des Hamiltonoperators<br />
ϕ2(r1, r2) = χA(r2)χB(r1) (193)<br />
als gleichwertige Näherung betrachten. Da die Elektronen Fermionen mit Spin<br />
1 sind, müssen wir aus (192) <strong>und</strong> (193) symmetrische o<strong>der</strong> antisymmetrische<br />
2<br />
Wellenfunktionen<br />
ϕ± = ϕ1 ± ϕ2<br />
(194)<br />
bilden, je nachdem <strong>der</strong> Spin antiparallel o<strong>der</strong> parallel ausgerichtet ist. Mit dieser —<br />
allein aus dem Gr<strong>und</strong>zustand des Wasserstoff–Atoms konstruierten — Näherung<br />
<strong>für</strong> die Wellenfunktion berechnen wir die Näherung<br />
E± = 〈ϕ±|H|ϕ±〉<br />
〈ϕ±|ϕ±〉<br />
<strong>für</strong> die Energie des Systems <strong>der</strong> beiden Elektronen <strong>und</strong> erhalten unter Ausnutzung<br />
<strong>der</strong> Symmetrie<br />
E± = 〈ϕ1|H|ϕ1〉 ± 〈ϕ1|H|ϕ2〉<br />
. (195)<br />
1 + 〈ϕ1|ϕ2〉<br />
Dabei geht 〈ϕ1|H|ϕ1〉 <strong>für</strong> große Abstände a in die Energie E1 = −2R <strong>der</strong> Gr<strong>und</strong>zustände<br />
<strong>der</strong> Wasserstoffatome über. Den entscheidenden Beitrag <strong>der</strong> Wechselwirkung<br />
beschreibt das Austauschintegral 〈ϕ1|H|ϕ2〉.<br />
Mit <strong>der</strong> Näherung (195) kann man E± in Abhängigkeit von a explizit berechnen<br />
<strong>und</strong> findet E± → ∞ <strong>für</strong> a → 0 <strong>und</strong> E± → −2R <strong>für</strong> a → ∞. Aber während E− (antisymmetrische<br />
Wellenfunktion, paralleler Spin) dabei monoton fällt, durchläuft<br />
E+ (symmetrische Wellenfunktion, antiparalleler Spin) dabei ein Minimum bei<br />
am ≈ 8 · 10 −11 m:<br />
82
−2R<br />
E<br />
E − (↑↑)<br />
a m<br />
E + (↑↓)<br />
Da −dE/da als Kraft auf die beiden Atome 30 wirkt, bleiben die beiden Atome bei<br />
antiparallelem Elektronenspin im Abstand am stabil beieinan<strong>der</strong>: Ein H2–Molekül<br />
ist gebildet.<br />
Die Bindung ist nur bei antiparallelem Spin möglich, da hier die beiden Elektronen<br />
einen gemeinsamen Ortszustand besetzen <strong>und</strong> sich in <strong>der</strong> Mitte <strong>der</strong> Kerne<br />
“konzentrieren” können. Dabei überwiegt die Anziehung zwischen Elektronen<br />
<strong>und</strong> Kernen die gegenseitige Abstoßung <strong>der</strong> Elektronen <strong>und</strong> hält das Molekül<br />
zusammen.<br />
Da die effektive Kraft, die die beiden Atome bindet, entscheidend auf dem Elektronenaustausch<br />
beruht, wird sie auch Austauschkraft genannt. Dieser gebräuchliche<br />
Name führt allerdings leicht zu einem Mißverständnis. Die Austauschkraft<br />
beruht nämlich keineswegs auf einer neuen mystischen “Quantenkraft”, die wir<br />
klassisch nicht verstehen, son<strong>der</strong>n einzig auf <strong>der</strong> wohlvertrauten Coulombwechselwirkung.<br />
Diese Wechselwirkung wird allerdings – <strong>und</strong> hier kommt die <strong>Quantenmechanik</strong><br />
ins Spiel – durch den Austauscheffekt bzw. das Pauliprinzip so modifiziert,<br />
daß sie ein Potentialminimum bildet <strong>und</strong> so die Bindung <strong>der</strong> beiden Atome<br />
ermöglicht.<br />
30 Wegen <strong>der</strong> großen Massen brauchen wir diese nicht quantenmechanisch zu beschreiben.<br />
83<br />
a
5 Die Interpretation <strong>der</strong> <strong>Quantenmechanik</strong><br />
Wir beenden die Analyse spezieller Probleme <strong>und</strong> wenden uns wie<strong>der</strong> <strong>der</strong> allgemeinen<br />
Diskussion <strong>der</strong> Interpretation <strong>der</strong> <strong>Quantenmechanik</strong> zu. Dazu stellen wir<br />
zunächst noch einmal die Gr<strong>und</strong>züge des Formalismus zusammen <strong>und</strong> bringen<br />
einige Ergänzungen an.<br />
5.1 Der Formalismus<br />
Die quantenmechanischen Systeme – o<strong>der</strong> besser: Unsere Erwartungen bei ihrer<br />
Beobachtung – werden durch Zustandsvektoren (Zustandsfunktionen)<br />
|ψ〉 = ψ(r, t), (196)<br />
beschrieben. Das Absolutquadrat ψ ∗ ψ gibt nach Born die Wahrscheinlichkeitsdichte<br />
an, das System bei r zu finden. Dynamische Variable A(r, p) <strong>und</strong> sonstige<br />
Observable (z. B. Spin) werden durch quantenmechanische Operatoren, die auf<br />
|ψ〉 wirken, repräsentiert. Speziell dem Impuls eines Teilchens ist <strong>der</strong> Operator<br />
zugeordnet.<br />
p = ¯h<br />
∇ (197)<br />
i<br />
In <strong>der</strong> klassischen Mechanik läßt sich <strong>der</strong> Wert A(t) = A(r(t), p(t)) einer dynamischen<br />
Variablen im Prinzip präzise berechnen. Dagegen lassen sich zu den<br />
quantenmechanischen Observablen A im allgemeinen “nur” Erwartungswerte<br />
〈A〉 = 〈ψ|A|ψ〉 (198)<br />
angeben. Die For<strong>der</strong>ung reeller Erwartungswerte wird durch hermitesche Operatoren<br />
sichergestellt. Der entscheidende Unterschied zur klassischen Mechanik ist<br />
darin begründet, daß Operatoren im allgemeinen nicht vertauschbar sind, daß<br />
also <strong>der</strong> Kommutator<br />
[A, B] = AB − BA (199)<br />
nicht verschwindet. Aus Gl.(197) folgen die speziellen Kommutatoren<br />
[pi, xj] = ¯h ∂xj<br />
i ∂xi<br />
84<br />
= ¯h<br />
i δij. (200)
Man kann statt von Gl.(197) direkt von den Vertauschungsrelationen (200) ausgehen<br />
<strong>und</strong> die ganze <strong>Quantenmechanik</strong> algebraisch aufbauen. Gl.(197) ist dann nur<br />
eine spezielle Darstellung, die Ortsdarstellung. Statt r kann man beispielsweise<br />
auch p als Variable benutzen <strong>und</strong> eine Zustandsfunktion ˜ ψ(p, t) definieren. Den<br />
Vertauschungsregeln (200) entsprechend wird dann <strong>der</strong> Ort durch den Operator<br />
r = i¯h d<br />
dp<br />
repräsentiert. Diese äquivalente Darstellung wird Impulsdarstellung 31 genannt.<br />
Die zeitliche Entwicklung des Zustandsvektors folgt <strong>der</strong> Schrödingergleichung<br />
i¯h ∂<br />
|ψ〉 = H|ψ〉 , (201)<br />
∂t<br />
wobei H den Hamiltonoperator bezeichnet. (Diese Gleichung gilt in je<strong>der</strong> Darstellung,<br />
aber nicht in jedem Bild, s. u.). Für den Erwartungswert 〈A〉 erhält man<br />
damit<br />
d<br />
dt 〈A〉 = 〈ψ|A| ˙ ψ〉 + 〈 ˙ ψ|A|ψ〉<br />
= 1<br />
1<br />
〈ψ|AH|ψ〉 −<br />
i¯h i¯h 〈ψ|HA|ψ〉<br />
= 1<br />
〈ψ|(AH − HA)|ψ〉<br />
i¯h<br />
o<strong>der</strong> – in Verallgemeinerung <strong>der</strong> Ehrenfest-Beziehungen (69, 70) –<br />
d 1<br />
〈A〉 = 〈[A, H]〉. (202)<br />
dt i¯h<br />
Dieses Ergebnis läßt sich auch an<strong>der</strong>s interpretieren: Statt die Zustände als Funktionen<br />
<strong>der</strong> Zeit zu betrachten (Schrödingerbild) <strong>und</strong> mit <strong>der</strong> Schrödingergleichung<br />
zu berechnen, können wir die Zustände festhalten <strong>und</strong> den Operatoren eine<br />
eigene Zeitabhängigkeit zubilligen (Heisenbergbild). Dieses alternative Bild<br />
lehnt sich also im Gr<strong>und</strong>e noch enger an die klassische Mechanik an. Die Operatoren<br />
AH des Heisenbergbildes genügen dann <strong>der</strong> Heisenberggleichung<br />
d<br />
dt AH = 1<br />
i¯h [AH, H] . (203)<br />
31 Orts– <strong>und</strong> Impulsdarstellung gehen durch eine Fouriertransformation auseinan<strong>der</strong> hervor.<br />
85
Man beachte, daß die Gl. (201) <strong>und</strong> (203) zu verschiedenen Bil<strong>der</strong>n gehören <strong>und</strong><br />
nicht nebeneinan<strong>der</strong> benutzt werden dürfen. Um daran zu erinnern, haben wir<br />
die Operatoren AH des Heisenbergbildes durch den Index H gekennzeichnet 32 .<br />
Erfüllt <strong>der</strong> Zustandsvektor |u〉 die Gleichung<br />
A|u〉 = a|u〉, (204)<br />
so heißt |u〉 Eigenvektor (Eigenfunktion) <strong>und</strong> a Eigenwert des Operators A. Die<br />
Eigenwerte hermitescher Operatoren sind reell <strong>und</strong> die Eigenfunktionen zu verschiedenen<br />
Eigenwerten sind orthogonal. Die Gesamtheit {aν} <strong>der</strong> Eigenwerte<br />
nennt man das Spektrum des Operators A. Wir übergehen hier die formalen<br />
Schwierigkeiten, die mit kontinuierlichen Spektren verb<strong>und</strong>en sind <strong>und</strong> <strong>und</strong> setzen<br />
voraus, daß A ein diskretes Spektrum <strong>und</strong> ein vollständiges System normierter<br />
Eigenvektoren mit<br />
〈uν|uµ〉 = δνµ<br />
besitzt. Dann läßt sich je<strong>der</strong> beliebige Zustandsvektor in <strong>der</strong> Form<br />
(205)<br />
|ψ〉 = <br />
cν|uν〉 (206)<br />
ν<br />
nach den Eigenvektoren von A entwickeln. (Als Beispiel hatten wir die Entwicklung<br />
nach den Eigenfunktionen des Hamiltonoperators kennengelernt.) Damit<br />
erhält man den Erwartungswert<br />
o<strong>der</strong> wegen (204) <strong>und</strong> (205)<br />
Entsprechende Beziehungen<br />
〈A〉 = 〈ψ|A|ψ〉 = <br />
c<br />
ν,µ<br />
∗ νcµ〈uν|A|uµ〉 〈A〉 = <br />
c ∗ νcµaµ〈uν|uµ〉 = <br />
c ∗ νcνaν.<br />
ν,µ<br />
〈A n 〉 = <br />
c ∗ νcνa n ν <strong>und</strong> 〈f(A)〉 = <br />
c ∗ νcνf(aν) (207)<br />
ν<br />
gelten dann auch <strong>für</strong> alle Potenzen von A <strong>und</strong> schließlich <strong>für</strong> alle hinreichend<br />
gutartigen Funktionen f(A). Daraus läßt sich zeigen 33 :<br />
32 Der Hamiltonoperator stimmt in beiden Bil<strong>der</strong>n überein.<br />
33 siehe z.B. Messiah, Bd. 1, Abschnitt 5.2.3.<br />
86<br />
ν<br />
ν
- Die einzigen Werte, die eine Observable A annehmen kann, sind die Eigenwerte<br />
aν des Operators A.<br />
- Die Wahrscheinlichkeit w(aν), daß die Observable A den Wert aν annimmt,<br />
ist durch<br />
(208)<br />
gegeben.<br />
w(aν) = c ∗ ν cν<br />
Die Interpretation des Absolutquadrats <strong>der</strong> Entwicklungskoeffizienten cν als Wahrscheinlichkeit<br />
<strong>für</strong> die Realisierung des speziellen Wertes aν <strong>der</strong> Observablen A geht<br />
ebenfalls auf Born zurück.<br />
5.2 Meßprozeß <strong>und</strong> Zustandsvektor<br />
Der soweit skizzierte Formalismus <strong>und</strong> seine Interpretation weisen noch einen<br />
entscheidenden Mangel auf: Um zu unseren Erwartungswerten <strong>und</strong> Wahrscheinlichkeiten<br />
zu kommen, müssen wir den Zustandsvektor kennen. Der aber läßt<br />
sich nur dann aus <strong>der</strong> Schrödingergleichung 34 berechnen, wenn wir den Anfangszustand<br />
|ψ〉t=0 spezifizieren können. Wie aber sollen wir einen Zustandsvektor<br />
festlegen, dem wir gar keine unmittelbare physikalische Bedeutung zubilligen?<br />
Jede physikalische Information muß natürlich letztlich aus Messungen gewonnen<br />
werden, <strong>und</strong> wir beantworten die oben gestellte Frage aus einer Gr<strong>und</strong>annahme<br />
über ideale Messungen:<br />
• Wird eine ideale Messung “unmittelbar” wie<strong>der</strong>holt, so liefert sie mit Sicherheit<br />
das selbe Resultat.<br />
Diese Gr<strong>und</strong>annahme ist es wert, ein wenig darüber nachzudenken. Die <strong>Quantenmechanik</strong><br />
liefert uns ja häufig nur Wahrscheinlichkeitsaussagen. Im allgemeinen<br />
können wir ein Meßergebnis also nicht präzise vorhersagen. Ein Meßprozeß<br />
ist aber kein Würfelspiel mit unverbindlichem Ergebnis: Habe ich drei Augen<br />
gewürfelt, ist das <strong>für</strong> das Ergebnis einer Wie<strong>der</strong>holung des Wurfs ohne jeden Belang.<br />
Das Ergebnis einer Messung soll dagegen reproduzierbar sein, ein Vergleich<br />
mit dem Würfelspiel würde <strong>der</strong> Experimentalphysik – <strong>und</strong> letztlich <strong>der</strong> gesamten<br />
Naturwissenschaft – den Boden entziehen. Habe ich also den Wert a einer Observablen<br />
A gemessen, so soll dieser Wert verbindlich sein. Ich sage, die Observable<br />
A hat den Wert a, <strong>und</strong> das heißt: Für eine erneute Messung von A läßt sich<br />
<strong>der</strong> Wert a vorhersagen. Die erneute Messung muß natürlich so “unmittelbar”<br />
erfolgen, daß die Dynamik des Systems den Zustand noch nicht verän<strong>der</strong>t hat.<br />
34 Wir bleiben wie wir es gewohnt sind im Schrödingerbild.<br />
87
Wir kommen damit zur Ermittlung des Zustandsvektors |u〉t=0 aus einer Messung:<br />
Habe ich zur Zeit t = 0 den Wert ak einer Observablen A gemessen, so weiß ich,<br />
daß eine unmittelbar folgende identische Messung mit <strong>der</strong> Wahrscheinlichkeit 1<br />
wie<strong>der</strong> ak liefern würde. Aus Gl.(208) folgern wir w(ak) = c ∗ k ck = 1 <strong>und</strong> w(aν) =<br />
c ∗ ν cν = 0 <strong>für</strong> ν = k o<strong>der</strong> – abgesehen von einem belanglosen Phasenfaktor –<br />
|ψ〉t=0 = |uk〉. (209)<br />
Diesen Schluß können wir natürlich nur ziehen, wenn <strong>der</strong> Meßwert ak tatsächlich<br />
nur mit einem Eigenvektor |u〉k verträglich ist, wenn also <strong>der</strong> Eigenwert ak einfach<br />
ist. Das Problem <strong>der</strong> Entartung wird damit zu einem physikalischen Problem.<br />
Wenn wir etwa beim Wasserstoffatom die Energie En messen, so können wir<br />
noch nicht auf den Zustand schließen, da n 2 verschiedene Eigenfunktionen χnlm<br />
zum Eigenwert En gehören. An diesem Beispiel wird aber auch schon deutlich,<br />
wie diese Schwierigkeit zu beheben ist: Außer <strong>der</strong> Energie E müssen wir auch das<br />
Drehimpulsquadrat L 2 <strong>und</strong> die Drehimpulskomponente Lz bestimmen.<br />
Voraussetzung da<strong>für</strong>, daß zwei Operatoren A <strong>und</strong> B (etwa E <strong>und</strong> L 2 im obigen<br />
Beispiel) gemeinsame Eigenvektoren |u〉 besitzen, ist, daß A <strong>und</strong> B vertauschbar<br />
sind. Denn aus<br />
folgt ja sofort<br />
A|u〉 = a|u〉 <strong>und</strong> B|u〉 = b|u〉<br />
AB|u〉 = ab|u〉 = BA|u〉 .<br />
Umgekehrt können Observable, <strong>der</strong>en Operatoren vertauschbar sind, gleichzeitig<br />
scharf gemessen werden, sie sind kommensurabel. Darüber hinaus kann man<br />
zeigen, daß sich aus den Eigenvektoren vertauschbarer Operatoren immer eine<br />
gemeinsame Basis auswählen läßt.<br />
Damit ist auch das Problem <strong>der</strong> Entartung gelöst: Ich muß so viele kommensurable<br />
Observablen A, B, . . . messen, bis <strong>der</strong> Zustand (<strong>der</strong> gemeinsame Eigenvektor)<br />
|u〉 eindeutig festliegt, die Entartung also aufgehoben ist. Wir halten also fest:<br />
• Der Anfangszustand |ψ〉t=0 läßt sich durch eine geeignete Folge von Messungen<br />
kommensurabler Observablen eindeutig festlegen.<br />
Messungen kommensurabler Observablen heißen auch verträglich. Dagegen sind<br />
Messungen von Observablen A <strong>und</strong> B nicht verträglich, wenn die Operatoren A<br />
<strong>und</strong> B nicht vertauschbar sind. Zwischen A <strong>und</strong> B besteht nämlich dann eine<br />
Unschärfebeziehung [vgl. Gl. (78)]<br />
88
〈∆A 2 〉〈∆B 2 2 1<br />
〉 ≥ [A, B] ,<br />
2i<br />
die es verbietet, A <strong>und</strong> B gleichzeitig scharf zu messen.<br />
Und wenn ich trotzdem messe? Darf ich dann die Meßwerte nicht mehr ernst<br />
nehmen? Nehmen wir an, ich habe zuerst A (Ergebnis a) <strong>und</strong> dann B (Ergebnis<br />
b) gemessen. Nach unserer Gr<strong>und</strong>annahme über (ideale) Messungen müssen wir<br />
dann auf jeden Fall das Ergebnis b als verbindlich ansehen. Nach <strong>der</strong> Unschärfebeziehung<br />
muß dann aber <strong>der</strong> Wert <strong>der</strong> Observablen A wie<strong>der</strong> gänzlich unbestimmt<br />
sein: Das Meßergebnis a <strong>der</strong> ersten Messung wird also durch eine nicht verträgliche<br />
zweite Messung bedeutungslos – so bedeutungslos wie die Augenzahl beim<br />
Würfeln!<br />
In den meisten Fällen können wir uns diese befremdliche Tatsache mit <strong>der</strong> Störung<br />
durch den Meßprozeß erklären. Bringen wir beispielsweise im Heisenbergschen<br />
Gedankenexperiment <strong>der</strong> optischen Ortsbestimmung (vgl. Abschnitt 2.6) ein ruhendes<br />
Teilchen unter das Mikroskop, so kennen wir dessen Impuls p = 0 (1.<br />
Messung). Zur genauen Ortsbestimmung (2. Messung) müssen wir anschließend<br />
das Teilchen aber mit hochenergetischen Photonen beschießen, <strong>und</strong> dieser Beschuß<br />
macht das Ergebnis <strong>der</strong> vorherigen Impulsmessung bedeutungslos (Comptoneffekt).<br />
Allerding gibt es auch Fälle, in denen nicht so einfach zu verstehen<br />
ist, warum eine unverträgliche zweite Messung die erste Messung ungültig macht<br />
(siehe Abschnitt 5.3).<br />
Die Bestimmung des Zustandsvektors durch Messungen hat eine bedeutsame<br />
Konsequenz: Der Zustandsvektor wird durch den Meßprozeß im allgemeinen geän<strong>der</strong>t.<br />
Normalerweise wird |ψ〉 nämlich keineswegs als Eigenfunktion |uk〉 vorliegen.<br />
Vielmehr wird sich |ψ〉 nach <strong>der</strong> Festlegung <strong>der</strong> Anfangsbedingungen durch frühere<br />
Messungen gemäß <strong>der</strong> Schrödingergleichung entwickeln <strong>und</strong> zum Meßzeitpunkt<br />
t0 − 0 in <strong>der</strong> allgemeinen Form (vgl. (206))<br />
|ψ〉t=t0−0 = <br />
cν|uν〉<br />
vorliegen. Messe ich also zum Zeitpunkt t = t0 die Observable A, so ist das Ergebnis<br />
nicht von vornherein determiniert, son<strong>der</strong>n kann mit <strong>der</strong> Wahrscheinlichkeit<br />
c ∗ ν cν jeden Wert aν annehmen. Nach <strong>der</strong> Messung (t = t0 + 0) steht das Ergebnis<br />
ar aber fest <strong>und</strong> soll verbindlich, also reproduzierbar sein. Daraus folgt wie oben,<br />
daß nach <strong>der</strong> Messung <strong>der</strong> Zustandsvektor<br />
vorliegt.<br />
ν<br />
|ψ〉t=t0+0 = |ur〉.<br />
Mit dem Meßprozeß ist also notwendigerweise eine spontane Än<strong>der</strong>ung<br />
89
|ψ〉t=t0−0 = <br />
cν|uν〉 −→ |ψ〉t=t0+0 = |ur〉 (210)<br />
ν<br />
des Zustandsvektors verb<strong>und</strong>en. Diese Än<strong>der</strong>ung wird als Reduktion des Zustandsvektors<br />
bezeichnet. Da hierbei aus <strong>der</strong> Summe <strong>der</strong> |uν〉 ein Eigenvektor |ur〉 “herausgefiltert”<br />
wird, spricht man auch von einem Filterprozeß.<br />
Dieser Filterprozeß wird keineswegs durch die Schrödingergleichung beschrieben,<br />
er wird vielmehr ad hoc durchgeführt, sobald das Ergebnis ar <strong>der</strong> Messung feststeht.<br />
Natürlich liegt es wie<strong>der</strong> nahe, diese unberechenbare Zustandsän<strong>der</strong>ung auf<br />
die Wechselwirkung mit dem Meßgerät zurückzuführen. Wir werden jedoch sehen,<br />
daß eine solche Interpretation in manchen Fällen problematisch ist.<br />
Wir können dem Problem ausweichen, wenn wir uns konsequent auf unsere Interpretation<br />
<strong>der</strong> <strong>Quantenmechanik</strong> beziehen: |ψ〉 beschreibt nicht ein physikalisches<br />
System an sich, son<strong>der</strong>n unsere Information über das System. Und diese Information<br />
än<strong>der</strong>t sich spontan durch einen Meßprozeß, genauer: durch die Kenntnisnahme<br />
des Meßresultats. Natürlich bringen wir genau damit den philosophischen<br />
Streit zwischen Positivisten <strong>und</strong> Realisten auf den Punkt: “Än<strong>der</strong>t sich das<br />
Weltall, wenn eine Maus es anschaut?” (Einstein).<br />
Nebenbei sei bemerkt, daß die Zustandsreduktion auch ein zweites Problem <strong>der</strong><br />
mo<strong>der</strong>nen Naturphilosophie tangiert: Sie ist nicht zeitumkehrinvariant.<br />
5.3 Das Einstein-Podolsky-Rosen–Paradoxon<br />
Die positivistische Interpretation <strong>der</strong> Kopenhagener Schule ist letztlich unangreifbar,<br />
da sie sich von vornherein auf Aussagen über die Beobachtung beschränkt.<br />
Und die Aussagen <strong>der</strong> <strong>Quantenmechanik</strong> über die Beobachtung sind nach unserem<br />
heutigen Wissenstand uneingeschränkt richtig. Trotzdem ist diese Interpretation<br />
unbefriedigend: Die Beobachtung hängt eben doch davon ab, ob eine Maus<br />
die Welt anschaut o<strong>der</strong> nicht. Dabei sind die meisten Menschen einschließlich<br />
<strong>der</strong> Theoretiker, solange sie nicht gerade die <strong>Gr<strong>und</strong>lagen</strong> <strong>der</strong> <strong>Quantenmechanik</strong><br />
diskutieren, überzeugt, daß es unabhängig von <strong>der</strong> Beobachtung eine objektive<br />
Realität gibt.<br />
Einstein, <strong>der</strong> sich nie mit dem Kopenhagener Positivismus anfre<strong>und</strong>en konnte,<br />
war deshalb überzeugt, daß die <strong>Quantenmechanik</strong> zwar richtig aber nicht<br />
vollständig ist. Unmittelbar nach seiner Emigration veröffentlichte er zusammen<br />
mit seinen Mitarbeitern Podolsky <strong>und</strong> Rosen eine Arbeit 35 unter dem Titel<br />
“Can Quantum–Mechanical Description of Physical Reality Be Consi<strong>der</strong>ed Complete?”,<br />
in <strong>der</strong> er seine Überzeugung an einem berühmt gewordenen Paradoxon<br />
demonstrierte.<br />
35 A. Einstein, B. Podolsky and N. Rosen, Phys. Rev. 47, 777 (1935)<br />
90
Die Arbeit tangiert natürlich die Grenzen zur Philosophie <strong>und</strong> beginnt deshalb<br />
mit begrifflichen Klarstellungen. Einstein, Podolsky <strong>und</strong> Rosen – im folgenden<br />
kurz EPR genannt – wi<strong>der</strong>stehen dabei <strong>der</strong> gefährlichen Versuchung, den Begriff<br />
<strong>der</strong> Vollständigkeit definieren zu wollen. Vielmehr begnügen sie sich mit <strong>der</strong><br />
Formulierung einer notwendigen Bedingung <strong>für</strong> die Vollständigkeit einer physikalischen<br />
Theorie:<br />
• Every element of the physical reality must have a counterpart in the physical<br />
theory.<br />
Akzeptiert man diese Bedingung, bleibt zu klären, was unter einem Element <strong>der</strong><br />
physikalischen Realität zu verstehen ist. Auch hier verzichten ERP auf eine umfassende<br />
Definition <strong>und</strong> begnügen sich mit einem konstruktiven Kriterium:<br />
• If, without in any way disturbing a system, we can predict with certainty (i.e.<br />
with probability equal to unity) the value of a physical quantity, then there<br />
exists an element of physical reality corresponding to this physical quantity.<br />
Man beachte, daß dieses Kriterium gezielt bei <strong>der</strong> Interpretation <strong>der</strong> Unschärfe<br />
durch die Störung bei einer Messung ansetzt! Und genau in <strong>der</strong> Konstruktion<br />
einer strungsfreien Messung inkommensurabler Größen liegt auch <strong>der</strong> Kern des<br />
EPR Gedankenexperiments (s.u.).<br />
Angewendet auf physikalische Observable, <strong>der</strong>en Operatoren nicht vertauschen,<br />
folgern EPR:<br />
entwe<strong>der</strong>: ”The quantum–mechanical desription of reality given by the wave<br />
function is not complete”<br />
o<strong>der</strong>: ”When the operators corresponding to two physical quantities do not commute<br />
the two quantities cannot have simultaneous reality,”<br />
also kurz: Entwe<strong>der</strong> ist die <strong>Quantenmechanik</strong> unvollständig o<strong>der</strong> konjugierte Observable<br />
wie x <strong>und</strong> p besitzen keine simultane Realität.<br />
Das konkrete Gedankenexperiment von EPR ist in dem Kasten auf <strong>der</strong> folgenden<br />
Seite dargestellt. Wir beziehen uns hier auf eine einfachere Variante, die auf Bohm<br />
zurückgeht36 . Bohm betrachtet zwei Spin 1<br />
2 –Teilchen, die aus dem Zerfall eines<br />
Teilchens mit Spin 0 hervorgehen. Da <strong>der</strong> Gesamtspin 0 erhalten bleibt, ist <strong>der</strong><br />
Spin <strong>der</strong> Teilchen 1 <strong>und</strong> 2 immer antiparallel. Messe ich also am Teilchen 1 die<br />
Spinkomponente s1ν <strong>und</strong> finde aν (= ±¯h/2), so weiß ich mit Sicherheit, daß ich<br />
bei Teilchen 2 die Spinkomponente s2ν = −aν finden werde.<br />
36 D. Bohm, Quantum Theory (Sec. 22.16), Prantice–Hall Inc., Englewood Cliffs (N.J.) 1951.<br />
91
Die Originalversion des EPR–Gedankenexperiments<br />
Zwei (eindimensionale) Teilchen wechselwirken<br />
im Zeitintervall [0, T ] <strong>und</strong> werden<br />
zu einem späteren Zeitpunkt t > T<br />
durch eine Wellenfunktion ψ(x1, x2) beschrieben.<br />
Diese Wellenfunktion können<br />
wir in <strong>der</strong> Form<br />
ψ(x1, x2) = <br />
ϕν(x2)uν(x1) bzw.<br />
ψ(x1, x2) = <br />
χµ(x2)vµ(x1)<br />
ν<br />
µ<br />
nach den Eigenfunktionen uν eines Operators<br />
A bzw. vµ eines Operators B des<br />
Teilchens 1 entwickeln. Die Entwicklungen<br />
sind verschieden, wenn A <strong>und</strong> B nicht vertauschen.<br />
Und nun führen wir eine Messung<br />
am Teilchen 1 durch, ohne das Teilchen<br />
2 auf irgendeine Weise zu stören; die<br />
Teilchen stehen ja nicht mehr miteinan<strong>der</strong><br />
in Wechselwirkung! Für die daraus folgende<br />
Reduktion <strong>der</strong> Wellenfunktion können<br />
wir zwei Fälle unterscheiden:<br />
1. Wir messen die Observable A, finden<br />
das Resultat ak <strong>und</strong> erhalten die neue<br />
Wellenfunktion ϕk(x2)uk(x1).<br />
2. Wir messen die Observable B, finden<br />
das Resultat br <strong>und</strong> erhalten die neue Wellenfunktion<br />
χr(x2)vr(x1).<br />
Wir müssen dem Teilchen 2 <strong>für</strong> sich allein<br />
betrachtet also je nach <strong>der</strong> Messung am<br />
Teilchen 1 zwei verschiedene Wellenfunktionen<br />
ϕk(x2) <strong>und</strong> χr(x2)<br />
zubilligen. Das Paradoxon wird komplett,<br />
wenn man annimmt (s. u.), daß ϕk(x2)<br />
<strong>und</strong> χr(x2) Eigenfunktionen nicht vertauschbarer<br />
Operatoren P <strong>und</strong> Q des<br />
Teilchens 2 sind. Dann können wir uns<br />
nämlich durch eine Messung am Teilchen<br />
1, also ohne das Teilchen 2 auf irgendeine<br />
Weise zu stören, entwe<strong>der</strong> den scharfen<br />
Wert p von P o<strong>der</strong> den scharfen Wert<br />
q von Q beschaffen. P <strong>und</strong> Q sollten also<br />
nach dem EPR–Realitätskriterium simultane<br />
Elemente <strong>der</strong> Realität sein.<br />
92<br />
Allerdings sind sie nicht – we<strong>der</strong> direkt<br />
noch auf dem Umweg über Teilchen 1 –<br />
simultan meßbar. Daraus schließen EPR,<br />
daß die <strong>Quantenmechanik</strong> unvollständig<br />
ist.<br />
Zur Bestätigung <strong>der</strong> entscheidenden Arbeitshypothese,<br />
daß ϕk(x2) <strong>und</strong> χr(x2)<br />
tatsächlich Eigenfunktionen nicht vertauschbarer<br />
Operatoren sein können, gehen<br />
EPR von <strong>der</strong> speziellen Wellenfunktion<br />
ψ(x1, x2) = 2π¯hδ(x1 − x2 + x0) =<br />
∞<br />
−∞<br />
e i<br />
¯h (x1−x2+x0)p dp .<br />
aus. Sie beschreibt ein System von zwei<br />
Teilchen mit scharfer Relativkoordinate<br />
x2−x1 = x0. Dementsprechend ist <strong>der</strong> Relativimpuls<br />
völlig unbestimmt, während<br />
<strong>der</strong> Gesamtimpuls (= 0, s. u.) wie<strong>der</strong> bekannt<br />
ist.<br />
Ist nun A <strong>der</strong> Impuls des Teilchens 1, so<br />
erhält man die Eigenfunktionen up(x1) =<br />
e i<br />
¯h x1p zum Eigenwert p. Das liefert die<br />
Entwicklung<br />
<br />
ψ(x1, x2) = ϕp(x2)up(x1)dp mit<br />
i −<br />
ϕp(x2) = e ¯h (x2−x0)p .<br />
Die Entwicklungskoeffizienten ϕp(x2) sind<br />
aber gerade die Eigenfunktionen des Impulsoperators<br />
P = −i¯h∂/∂x2 des Teilchens<br />
2 zum Eigenwert −p. Daher haben<br />
wir einen scharfen Gesamtimpuls p +<br />
(−p) = 0.<br />
Ist an<strong>der</strong>erseit B <strong>der</strong> Ort des Teilchens<br />
1, so erhält man die Eigenfunktionen<br />
vx(x1) = δ(x1 − x) zum Eigenwert x. Daraus<br />
folgt die Entwicklung<br />
<br />
ψ(x1, x2) = χx(x2)vx(x1)dx mit<br />
χx(x2) = 2π¯hδ(x − x2 + x0).<br />
Die Entwicklungskoeffizienten χx(x2) sind<br />
also die Eigenfunktionen des Ortsoperators<br />
Q = x2 des Teilchens 2 zum Eigenwert<br />
x + x0.
Da sich <strong>der</strong> Experimentator nach dem Zerfall, also zu einer Zeit, wo er das Teilchen<br />
2 in keiner Weise stört, frei entscheiden kann, welche Spinkomponente des<br />
Teilchens 1 er mißt, schließt er mit EPR, daß sämtliche Spinkomponenten des<br />
Teilchens 2 wohldefiniert vorliegen müssen: Die Information darüber ist ja offenbar<br />
in dem separierten Teilchen 1 “gespeichert”. Alle Spinkomponenten des<br />
Teilchens 2 sind also Elemente <strong>der</strong> physikalischen Realität im Sinne des oben<br />
formulierten EPR–Kriteriums.<br />
Da <strong>der</strong> Spin den Rechenregeln des Drehimpulses folgt, gestattet die <strong>Quantenmechanik</strong><br />
aber jeweils nur die Festlegung einer Spinkomponente, <strong>und</strong> EPR schließen<br />
folglich, daß die <strong>Quantenmechanik</strong> nicht vollständig ist. Dieses Paradoxon wirft<br />
bis heute ernsthafte Probleme auf, <strong>und</strong> B. d’ Espagnat bemerkt: “Kein Theoretiker,<br />
<strong>für</strong> den die Physik mehr ist als <strong>der</strong> Vorwand zu einem schönen Formalismus,<br />
kann sich unserer Ansicht nach nicht davon betroffen fühlen.”<br />
Bohrs Antwort zu EPR erschien postwendend unter dem selben Titel 37 . Im Gegensatz<br />
zu <strong>der</strong> kompakten <strong>und</strong> einleuchtend erscheinenden Darstellung von EPR<br />
macht Bohr es dem Leser jedoch nicht ganz leicht, die klare Entgegnung zum<br />
Kern des Paradoxons zu erkennen. Er wie<strong>der</strong>holt die Kopenhagener Positionen<br />
<strong>und</strong> versucht, diese Interpretation durch eine detaillierte <strong>und</strong> spitzfindige Diskussion<br />
verschiedener Experimente zu verdeutlichen.<br />
Die eigentliche Kritik Bohrs setzt beim EPR–Kriterium <strong>für</strong> physikalische Realität<br />
ein. Bohr billigt nämlich inkommensurablen Observablen keine simultane<br />
Realität zu, da sie nicht simultan beobachtbar sind (Positivismus!).<br />
Es ist also nicht nur überflüssig (Feynman) nach dem Ort <strong>und</strong> dem Impuls eines<br />
Teilchens zu fragen, son<strong>der</strong>n sinnlos, da Ort <strong>und</strong> Impuls keine a priori Realität zukommt.<br />
Sie werden vielmehr erst durch den Meßprozeß realisiert, <strong>und</strong> die Aussage<br />
“Der Experimentator hätte ja auch die komplementäre Variable messen können”,<br />
ist eben kein Meßprozeß. (Daß einem präzise vorhersagbaren Phänomen nicht<br />
notwendigerweise eine von den Beobachtungsbedingungen unabhängige a priori–<br />
Existenz zukommt, mag man sich am Schatten klarmachen!)<br />
Ein Gedicht ist lediglich eine mehr o<strong>der</strong> weniger unregelmäßige Verteilung von<br />
Druckerschwärze auf weißem Papier, solange kein Bewußtsein das Zeichenmuster<br />
aufnimmt, interpretiert <strong>und</strong> damit zum Gedicht macht. Und ebenso wird eine<br />
Meßgröße erst durch den Meßvorgang (einschließlich <strong>der</strong> Kenntnisnahme des Resultats)<br />
“verwirklicht”. Da es aber keinen Meßvorgang gibt, <strong>der</strong> x <strong>und</strong> p (o<strong>der</strong><br />
sämtliche Spinkomponenten) simultan “verwirklicht”, kommt ihnen auch keine<br />
simultane Realität zu. Diese positivistische Geisteshaltung, die zu Beginn des<br />
zwanzigsten Jahrhun<strong>der</strong>ts “in Mode kam”, wird schön durch ein Gedicht Christian<br />
Morgensterns 38 dokumentiert:<br />
37 N. Bohr, Phys. Rev. 48, 696 (1935)<br />
38 1867–1914; aus Palma Kunkel (1916).<br />
93
Tief im dunklen Walde steht er,<br />
<strong>und</strong> auf ihm mit schwarzer Farbe,<br />
daß des Wandrers Geist nicht darbe:<br />
Drei<strong>und</strong>zwanzig Kilometer.<br />
Der Meilenstein<br />
Ja, noch weiter vorgestellt:<br />
Was wohl ist er ungesehen?<br />
ein uns völlig fremd Geschehen.<br />
Erst das Auge schafft die Welt.<br />
5.4 Schrödinger <strong>und</strong> seine Katze<br />
Seltsam ist <strong>und</strong> schier zum Lachen,<br />
daß es diesen Text nicht gibt,<br />
wenn es keinem Blick beliebt,<br />
ihn durch sich zu Text zu machen.<br />
Auch Schrödinger war Anhänger des Realismus. Ihm hatte anfänglich eine<br />
reine Wellentheorie <strong>der</strong> Materie vorgeschwebt, in <strong>der</strong> Teilchen durch Wellenpakete<br />
repräsentiert sind. Von dieser Lieblingsvorstellung mußte er jedoch abrücken,<br />
da außer beim harmonischen Oszillator alle Wellenpakete im Laufe <strong>der</strong> Zeit auseinan<strong>der</strong>laufen.<br />
Im Jahr 1935 – kurz nach EPR – publizierte er einen Aufsatz 39<br />
“Über die gegenwärtige Situation in <strong>der</strong> <strong>Quantenmechanik</strong>”, in dem die gesamte<br />
Problematik scharfsinnig analysiert <strong>und</strong> ausgezeichnet dargestellt ist.<br />
Schrödinger weist zunächst darauf hin, daß die <strong>Quantenmechanik</strong> mit Begriffen<br />
arbeitet, die dem klassischen Modell (Ort, Impuls, . . . ; Bohrs Korrespondenzprinzip!)<br />
ohne Modifikation entnommen sind. Sie verwendet aber stets nur genau<br />
eine Hälfte des klassischen Variablensatzes 40 <strong>und</strong> bringt so statistische Aussagen<br />
ins Spiel. Die ψ–Funktion repräsentiert daher einen Erwartungskatalog. Dabei<br />
kann die <strong>Quantenmechanik</strong> aber nicht einfach als Theorie eines klassischen Ensembles<br />
verstanden werden. Denn damit ließe sich we<strong>der</strong> verstehen, warum etwa<br />
<strong>der</strong> Drehimpuls von jedem Koordinatenursprung aus gequantelt erscheint noch<br />
ließe sich eine Aufenthaltswahrscheinlichkeit im klassisch verbotenen Bereich erklären.<br />
Einen empirischen Standpunkt lehnt Schrödinger nicht gr<strong>und</strong>sätzlich ab, verwahrt<br />
sich aber dagegen, ihn “als Diktator zur Hilfe zu rufen in den Nöten physikalischer<br />
Methodik”. Damit ist <strong>der</strong> Vollständigkeitsanspruch Kopenhagens angesprochen.<br />
Er geht auch bereits auf EPR ein <strong>und</strong> bettet die Diskussion in eine<br />
sorgfältige Analyse von Meßprozeß <strong>und</strong> maximaler Kenntnis. Die Zustandsreduktion<br />
– nach Schrödinger <strong>der</strong> interessanteste Punkt <strong>der</strong> Theorie – wird als<br />
geän<strong>der</strong>ter Erwartungskatalog interpretiert.<br />
Was die Arbeit jedoch berühmt gemacht hat, ist die Konstruktion eines “burlesken<br />
Falles”, <strong>der</strong> ein neues Paradoxon aufzeigt: Schrödingers Katze.<br />
39 E.Schrödinger, Die Naturwissenschaften 23, 807 <strong>und</strong> 844 (1935).<br />
40 Man beachte dabei die Analogie <strong>und</strong> den Unterschied zur Hamilton–Jakobi–Theorie.<br />
94
Eine Katze wird in einen <strong>und</strong>urchsichtigen Kasten gesperrt, in dem ein radioaktives<br />
Präparat über einen Geigerzähler einen Hammermechanismus auslösen kann,<br />
<strong>der</strong> eine Ampulle mit Blausäure zerschlägt. Nach einer St<strong>und</strong>e sei die Katze mit<br />
<strong>der</strong> Wahrscheinlichkeit 1<br />
2 vergiftet.<br />
Die <strong>Quantenmechanik</strong> beschreibt das System mit einem Zustandsvektor, <strong>der</strong> die<br />
Wahrscheinlichkeit 1 korrekt angibt. Erst nach Öffnen des Deckels (Messung!)<br />
2<br />
wird <strong>der</strong> Zustand reduziert <strong>und</strong> beschreibt die lebendige o<strong>der</strong> die tote Katze.<br />
Kann diese Beschreibung vollständig sein? Ist die Katze nicht auch vor dem Öffnen<br />
des Deckels entwe<strong>der</strong> lebendig o<strong>der</strong> tot? Ein ganz konsequenter Kopenhagener<br />
muß diese Frage als sinnlos ablehnen. Allen weniger konsequenten Menschen<br />
bleibt nur <strong>der</strong> Ausweg über eine Ensemble–Interpretation. Die aber ist (s. o.) <strong>für</strong><br />
die mikroskopischen Quantensysteme zumindest zweifelhaft.<br />
5.5 Verborgene Parameter <strong>und</strong> Bohms Interpretation<br />
Die statistische Interpretation <strong>der</strong> <strong>Quantenmechanik</strong> ist mit einem deterministischen<br />
Weltbild vereinbar, wenn man annimmt, daß alle “Zufälligkeiten” auf<br />
den zufälligen Konstellationen verborgener Parameter beruhen. Solche verborgenen<br />
Parameter benutzt ja auch die klassische <strong>Statistik</strong>, etwa die Koordinaten<br />
<strong>und</strong> Impulse sämtlicher Moleküle in <strong>der</strong> kinetischen Gastheorie. Entsprechende<br />
Bestrebungen in <strong>der</strong> <strong>Quantenmechanik</strong> wurden jedoch zunächst aufgegeben, als<br />
von Neumann 1932 bewiesen hatte 41 , daß eine deterministische Beschreibung<br />
mit irgendwie gearteten verborgenen Parametern gr<strong>und</strong>sätzlich mit <strong>der</strong> <strong>Quantenmechanik</strong><br />
unvereinbar ist. Interessanterweise wird dieser Beweis we<strong>der</strong> von EPR<br />
<strong>und</strong> Schrödinger noch von Bohr erwähnt. Aus heutiger Sicht ist <strong>der</strong> Beweis<br />
nicht zwingend, da die Voraussetzungen zu eng gefaßt sind (Bell 1966).<br />
Auch Bohm ging nicht auf von Neumanns Satz ein, als er 1952 unter dem Titel<br />
”A suggested interpretation of the quantum theory in terms of hidden variables”<br />
eine deterministische Interpretation <strong>der</strong> <strong>Quantenmechanik</strong> entwarf 42 . Dazu ging<br />
er von <strong>der</strong> Schrödingergleichung<br />
i¯h ∂ψ<br />
∂t<br />
aus <strong>und</strong> formte sie über den Phasenansatz<br />
¯h2<br />
= − ∆ψ + V (x)ψ (211)<br />
2m<br />
ψ(x, t) = ρ 1<br />
<br />
i<br />
2 (x, t) exp S(x, t)<br />
¯h<br />
(212)<br />
41 J. von Neumann, Mathematische <strong>Gr<strong>und</strong>lagen</strong> <strong>der</strong> <strong>Quantenmechanik</strong>, Springer, Berlin 1932<br />
42 D. Bohm, Phys. Rev. 85, 166 (1952).<br />
95
in das gekoppelte Gleichungssystem<br />
∂S<br />
∂t<br />
+ (∇S)2<br />
2m<br />
<br />
∂ρ<br />
+ ∇ · ρ<br />
∂t ∇S<br />
<br />
m<br />
¯h2<br />
+ V −<br />
4mρ2 <br />
ρ∆ρ − 1<br />
2 (∇ρ)2<br />
<br />
= 0 (213)<br />
= 0 (214)<br />
<strong>für</strong> die beiden reellen Funktionen S <strong>und</strong> ρ um. Dabei ist ρ = ψ ∗ ψ die quantenmechanische<br />
Wahrscheinlichkeitsdichte.<br />
Für ¯h → 0 geht Gl.(214) in die Hamiltonsche partielle Differentialgleichung 43 <strong>der</strong><br />
klassischen Mechanik über, wobei S = Ldt die Wirkungsfunktion ist. Mit<br />
p = ∇S bzw. v = ∇S<br />
m<br />
erkennt man dazu in Gl.(213) die Kontinuitätsgleichung.<br />
Bohms Idee bestand nun darin, diese klassische Beschreibung auch <strong>für</strong> ¯h = 0<br />
beizubehalten. Dazu ergänzte er das klassische Potential V (x) durch das “Quantenpotential”<br />
U(x, t) = − ¯h2<br />
4mρ2 <br />
ρ∆ρ − 1<br />
2 (∇ρ)2<br />
<br />
. (215)<br />
Dieses Quantenpotential ist im allgemeinen eine rasch verän<strong>der</strong>liche Funktion<br />
des Ortes <strong>und</strong> <strong>der</strong> Zeit. Daraus resultieren starke, schwer überschaubare “Quantenkräfte”,<br />
die <strong>für</strong> sämtliche Quanteneffekte verantwortlich sind. ρ o<strong>der</strong> die ψ–<br />
Funktion wirkt also wie ein Feld <strong>der</strong> klassischen Physik, welches das Teilchen<br />
“führt”. Eine ähnliche Idee hatte de Broglie bereits 1928 entwickelt, sie aber<br />
nach anfänglichen Schwierigkeiten nicht weiter verfolgt.<br />
In dieser Interpretation wird mit jedem quantenmechanischen Teilchen ein klassisches<br />
Teilchen assoziiert, das exakt definierte <strong>und</strong> kontinuierlich variierende Orts<strong>und</strong><br />
Impulswerte besitzt, die uns nur nicht bekannt sind (verborgene Parameter!).<br />
Die ψ–Funktion spielt eine doppelte Rolle: Sie wirkt einerseits auf dieses Teilchen<br />
wie ein Feld <strong>der</strong> klassischen Physik. An<strong>der</strong>erseits repräsentiert sie ein statistisches<br />
Ensemble mit <strong>der</strong> Wahrscheinlichkeitsdichte ρ = |ψ| 2 , das unsere Unkenntnis wi<strong>der</strong>spiegelt.<br />
Die <strong>Statistik</strong> ist also nicht a priori inhärent, son<strong>der</strong>n stellt nur eine<br />
praktische Notwendigkeit dar, da wir die Anfangsorte <strong>und</strong> Anfangsgeschwindigkeiten<br />
nicht kennen.<br />
43 Dieser Zusammenhang ist nicht neu <strong>und</strong> wurde verschiedentlich genutzt, um die klassische<br />
Mechanik mit <strong>der</strong> geometrischen Optik zu vergleichen.<br />
96
Bohm diskutiert eine Reihe von Beispielen, an denen er seine Interpretation illustriert.<br />
So ist in stationären Zuständen das Teilchen tatsächlich in Ruhe, da sich<br />
die klassische Kraft <strong>und</strong> die Quantenkraft gegenseitig aufheben. Beim Tunneleffekt<br />
ermöglichen die starken Schwankungen des Quantenpotentials, das Barriere–<br />
“Gebirge” in engen “Schluchten” <strong>und</strong> “Kanälen” zu durchqueren. Diese Beispiele<br />
machen deutlich, daß alle Quanteneffekte mit Bohms Interpretation verträglich<br />
sind. Das ist auch nicht verwun<strong>der</strong>lich, da die Interpretation ja auf <strong>der</strong> Schrödingergleichung<br />
basiert. Gerade hier liegt aber auch ihre Schwäche: Diese Interpretation<br />
ist prinzipiell nicht beweisbar <strong>und</strong> damit aus Kopenhagener Sicht überflüssig:<br />
Liefert sie doch kein Ergebnis, das von <strong>der</strong> üblichen <strong>Quantenmechanik</strong> abweicht.<br />
Immerhin zeigt sie – <strong>und</strong> allein das ist verdienstvoll genug – daß entgegen dem<br />
Kopenhagener Verbot deterministische Interpretationen möglich sind. Aus diesem<br />
Gr<strong>und</strong>e wurde sie auch in den 1990er Jahren neu aufgegriffen <strong>und</strong> erlebte<br />
eine kleine Renaissance.<br />
Wer aber in Bohms Interpretation die wahre realistische Lösung <strong>der</strong> quantenmechanischen<br />
Gr<strong>und</strong>probleme sehen möchte, dem sei doch ein bitterer Wermutstropfen<br />
in den süßen Wein gegossen: Man kommt ja nicht umhin, in <strong>der</strong> ψ–<br />
Funktion auch den Erwartungskatalog Schrödingers zu sehen, <strong>der</strong> den subjektiven<br />
Kenntnisstand wi<strong>der</strong>spiegelt: Daß dieser Kenntnisstand nun das Kraftfeld<br />
modifizieren soll, dem das Teilchen ausgesetzt ist, scheint doch wie<strong>der</strong> ins Reich<br />
<strong>der</strong> Magie zu führen.<br />
5.6 Lokalität <strong>und</strong> Bellsche Ungleichung<br />
Daß im EPR–Experiment die Messung am Teilchen 1 das Teilchen 2 in keiner<br />
Weise stört, wird aus <strong>der</strong> räumlichen Trennung gefolgert. Die anhaltende Diskussion<br />
des EPR-Paradoxons brachte daher in den folgenden Jahrzehnten die<br />
Gesichtspunkte <strong>der</strong>“Lokalität” <strong>und</strong> “Separabilität” ins Spiel: Sind räumlich getrennte,“nicht<br />
mehr wechselwirkende” Systeme wirklich völlig unabhängig voneinan<strong>der</strong><br />
<strong>und</strong> können separat betrachtet werden?<br />
Einstein wies mit Recht darauf hin, daß die Annahme <strong>der</strong> Separabilität räumlich<br />
getrennter Systeme eine notwendige Voraussetzung ist, überhaupt Physik zu<br />
betreiben <strong>und</strong> Naturgesetze zu formulieren. An<strong>der</strong>erseits ist die deterministische<br />
Bohmsche Interpretation sicherlich nicht lokal (Bell 1966): Die ψ–Funktion als<br />
“Feld” <strong>der</strong> Quantenkraft verschwindet nicht, wenn <strong>der</strong> Abstand <strong>der</strong> Teilchen groß<br />
wird. Und auch <strong>der</strong> Doppelspaltversuch, bei dem das Elektron “weiß”, ob <strong>der</strong> “an<strong>der</strong>e”<br />
Spalt geöffnet ist, legt eine Nicht–Lokalität physikalischer Erscheinungen<br />
nahe.<br />
Bell 44 entwickelte nun einen Gedanken, <strong>der</strong> die Frage nach <strong>der</strong> Lokalität <strong>und</strong>/o<strong>der</strong><br />
Separabilität experimentell entscheidbar macht. Dieser Gedanke geht von <strong>der</strong><br />
44 J. Bell, Physics 1,195 (1965)<br />
97
Bohmschen Version des EPR–Versuchs (Abschnitt 5.3) aus: Die beiden EPR–<br />
Teilchen seien Spin 1 –Teilchen, die aus dem Zerfall eines Teilchens mit Spin 0<br />
2<br />
hervorgehen. Wie im Abschnitt 5.3 besprochen, kann <strong>der</strong> Experimentator nach<br />
dem Zerfall, also zu einer Zeit, wo er das Teilchen 2 in keiner Weise stört, durch<br />
eine entsprechende Messung am Teilchen 1 frei entscheiden, welche Spinkomponente<br />
des Teilchens 2 er bestimmen möchte. Er schließt also mit EPR, daß<br />
sämtliche Spinkomponenten des Teilchens 2 wohldefiniert vorliegen müssen.<br />
Wir nehmen daher an, daß beide Teilchen einen wohldefinierten vektoriellen<br />
Spin 45 besitzen <strong>und</strong> untersuchen die x–y–Komponenten des Spins von Teilchen<br />
1 mit einem Analysator A1. Der Analysator wird in <strong>der</strong> Stellung α das Teilchen<br />
1 nur durchlassen, wenn s1α = +¯h/2 ist. Wir fragen nun mit Bell nach den<br />
Wahrscheinlichkeiten<br />
w(α1, α2, . . . |γ1, γ2, . . .) (216)<br />
da<strong>für</strong>, daß Teilchen 1 bei den Stellungen α1, α2, . . . von A1 durchgelassen wird,<br />
bei den Stellungen γ1, γ2, . . . dagegen nicht. Offenbar gilt <strong>für</strong> jedes β<br />
w(α|γ) = w(α|β, γ) + w(α, β|γ) ,<br />
denn in <strong>der</strong> Stellung β wird das Teilchen entwe<strong>der</strong> durchgelassen o<strong>der</strong> nicht.<br />
Außerdem gilt selbstverständlich<br />
w(α|β, γ) ≤ w(α|β) <strong>und</strong> w(α, β|γ) ≤ w(β|γ) .<br />
Daraus folgt bereits die berühmte Bellsche Ungleichung<br />
w(α|γ) ≤ w(α|β) + w(β|γ) . (217)<br />
Diese Ungleichung basiert wohlgemerkt auf <strong>der</strong> Annahme, daß die Teilchen einen<br />
wohldefinierten Spin besitzen, <strong>der</strong> unabhängig vom Experimentator <strong>und</strong> vom Rest<br />
<strong>der</strong> Welt festliegt. Vom empiristischen Standpunkt <strong>der</strong> Quantentheorie macht es<br />
nämlich überhaupt keinen Sinn, nach den Wahrscheinlichkeiten (216) zu fragen,<br />
da nur eine Messung mit genau einer Stellung des Analysators wirklich ausgeführt<br />
werden kann – mit einer entscheidenden Ausnahme:<br />
Die zwei–argumentigen Wahrscheinlichkeiten <strong>der</strong> Bellschen Ungleichung (217)<br />
lassen sich auch quantenmechanisch definieren. w(α|β) ist nämlich wegen <strong>der</strong><br />
antiparallelen Spins die Wahrscheinlichkeit da<strong>für</strong>, daß<br />
45 Dabei muß ich allerdings zugeben, daß ich mir einen Vektor, dessen Komponenten in jedem<br />
Koordinatensystem nur zwei diskrete Werte annehmen können, schwer vorstellen kann.<br />
98
- bei <strong>der</strong> Stellung α des Analysators A1 <strong>für</strong> Teilchen 1 <strong>und</strong><br />
- bei <strong>der</strong> Stellung β des Analysators A2 <strong>für</strong> Teilchen 2<br />
(siehe Skizze) beide Detektoren D1 <strong>und</strong> D2 ansprechen.<br />
D 1<br />
α<br />
A 1<br />
1<br />
Diese Wahrscheinlichkeit läßt sich quantenmechanisch berechnen <strong>und</strong> wird<br />
2<br />
A 2<br />
β<br />
D 2<br />
w(α|β) = 1 α − β<br />
sin2 . (218)<br />
2 2<br />
Wählt man speziell α = 0, β = π/4 <strong>und</strong> γ = π/2, so wird<br />
<strong>und</strong><br />
w(α|γ) = 1 π<br />
sin2<br />
2 4<br />
w(α|β) + w(β|γ) = 2 · 1 π<br />
sin2<br />
2 8<br />
= 0.25<br />
= 0.146 . . . .<br />
• Die <strong>Quantenmechanik</strong> verletzt also die Bellsche Ungleichung!<br />
Damit wird die EPR–Behauptung wohldefinierter Eigenschaften <strong>der</strong> separierten<br />
Teilchen nicht mehr lediglich ein Argument gegen die Vollständigkeit <strong>der</strong> <strong>Quantenmechanik</strong>,<br />
son<strong>der</strong>n ein Argument gegen ihre Gültigkeit!<br />
Die Frage <strong>Quantenmechanik</strong> o<strong>der</strong> EPR–Aussage ist damit zu einer experimentell<br />
prüfbaren Frage geworden. Entsprechende Experimente sind in den vergangenen<br />
Jahrzehnten mehrfach durchgeführt worden <strong>und</strong> haben die Gültigkeit von (218)<br />
bestätigt <strong>und</strong> (217) wi<strong>der</strong>legt. Die EPR-Teilchen 1 <strong>und</strong> 2 können also trotz ihrer<br />
räumlichen Trennung nicht separiert geshen werden, ihre Zustände bleiben<br />
“verschränkt”.<br />
99
Literaturhinweise<br />
1. <strong>Quantenmechanik</strong> allgemein<br />
Bei <strong>der</strong> Ausarbeitung dieser Vorlesung habe ich insbeson<strong>der</strong>e folgende Lehrbücher<br />
benutzt:<br />
a) A. Messiah: <strong>Quantenmechanik</strong>, Bd. 1, Walter de Gruyter, Berlin <strong>und</strong><br />
New York 1976<br />
b) L. Schiff: Quantum Mechanics, 3. Aufl., McGraw–Hill, New York 1968<br />
c) E. Fick: Einführung in die <strong>Gr<strong>und</strong>lagen</strong> <strong>der</strong> Quantentheorie, 2. Aufl.,<br />
AVG, Frankfurt 1972<br />
d) S.A. Davydov: <strong>Quantenmechanik</strong>, VEB Deutscher Verlag <strong>der</strong> Wissenschaften,<br />
Berlin 1978<br />
e) G. Süssmann: Einführung in die <strong>Quantenmechanik</strong>, <strong>Gr<strong>und</strong>lagen</strong> I, BI<br />
Mannheim Band 9/9a<br />
Diese Aufstellung <strong>der</strong> Quellen ist nicht als spezielle Empfehlung zu verstehen.<br />
Je nach persönlichem Geschmack eignen sich alle üblichen Lehrbücher<br />
<strong>der</strong> <strong>Quantenmechanik</strong>, in Ergänzung zum Skriptum einzelne Probleme nachzulesen<br />
o<strong>der</strong> zu vertiefen. Erwähnen möchte ich speziell<br />
f) Th. Fließbach: Lehrbuch zur Theoretische Physik III, Spektrum Akad.<br />
Verlag, Heidelberg-Berlin 2000 (4. Auflage 2005)<br />
g) Gernot Münster: Quantentheorie, Walter de Gruyter Berlin - New York<br />
2006<br />
All diese Lehrbcher gehen natürlich im Umfang wesentlich über den Inhalt<br />
dieser <strong>Gr<strong>und</strong>lagen</strong>-Vorlesung hinaus.<br />
2. Zur Interpretation <strong>der</strong> Quantentheorie<br />
a) F. Selleri: Die Debatte um die Quantentheorie, Vieweg 1983<br />
b) K. Baumann & R. U. Sexl: Die Deutungen <strong>der</strong> Quantentheorie, Vieweg<br />
1984 (Nach einer knappen Darstellung <strong>der</strong> Problematik enthält dieses<br />
Buch 12 historisch wie inhaltlich bedeutsame Originalarbeiten.)<br />
3. Ergänzende Literatur<br />
Daneben empfehle ich, zum besseren Verständnis des physikalischen Hintergr<strong>und</strong>s<br />
einzelne Kapitel in den ausgezeichneten Feynman Lectures nachzulesen:<br />
100
Feynman/Leighton/Sands: Vorlesungen über Physik, Bd. 1 <strong>und</strong> 2, R. Oldenbourg<br />
Verlag München<br />
Schließlich sei noch auf ein popularwissenschaftliches Buch hingewiesen, das<br />
ein leidenschaftliches Plädoyer gegen die übliche Kopenhagener Deutung<br />
darstellt <strong>und</strong> eine F<strong>und</strong>grube historischer Anmerkungen enthält:<br />
J. A. e Silva & G. Lochak: Wellen <strong>und</strong> Teilchen – Einführung in die <strong>Quantenmechanik</strong>,<br />
Fischer 6239 (1974)<br />
101