C:\mol\noter\Statistik\Statistiske grundbegreber-v11\s1v11-forside.wpd

MOGENS ODDERSHEDE LARSEN
18
15
12
9
6
3
0
STATISTISKE
GRUNDBEGREBER
med anvendelse af TI 89 og Excel
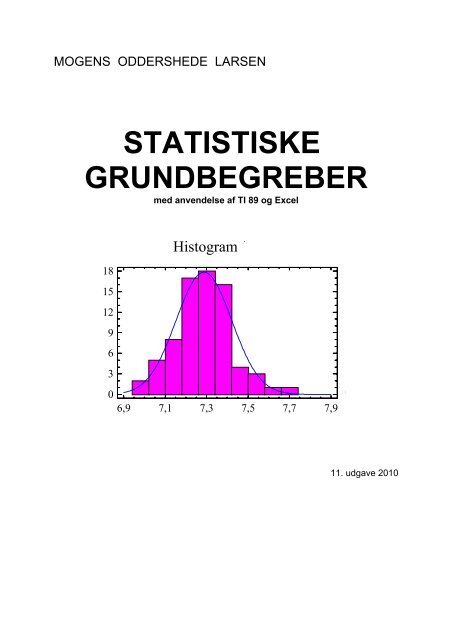
Histogram for pH
6,9 7,1 7,3 7,5 7,7 7,9
pH
11. udgave 2010

FORORD
Der er i denne bog søgt at give letlæst og anskuelig fremstilling af de statistiske grundbegreber til
brug ved en indledende undervisning i statistik. De væsentligste definitioner og sætninger forklares
derfor fortrinsvist ved hjælp af figurer og gennemregnede praktiske eksempler. Ønskes en mere
matematisk uddybende forklaring, bevis for sætninger osv. kan dette ofte findes i et særskilt tillæg
til bogen, som findes på nettet under titlen “Supplement til statistiske grundbegreber”.
Læsning: Bogen er bygget således op, at der hurtigt nås frem til normalfordelingen og de vigtige
normalfordelingstest. Disse vigtige begreber kan derfor blive grundigt indarbejdet, selv om der kun
er kort tid til rådighed. Er det af tidsmæssige grunde svært at nå hele notatet kan man uden skade for
helheden overspringe kapitlerne 10 og 11, ligesom man eventuelt kan tage kapitlerne 1 og 9 mere
oversigtsagtigt.
Sidst i hver kapitel findes en række opgaver, der yderligere kan fremme forståelsen.
Bagerst i bogen findes en facitliste til alle opgaverne.
I et længere kursusforløb er denne bog tænkt at skulle efterfølges af M. Oddershede Larsen:
Videregående Statistik”, som kan hentes gratis på e-mailadressen www.larsen-net.dk
Regnemidler. Det er hensigtsmæssigt, at man har adgang til en lommeregner eller en PC med
normalfordeling, t - fordeling, binomialfordeling og Poissonfordeling indbygget.
I eksemplerne angives således, hvorledes beregningerne kan foretages med den i øjeblikket mest
populære lommeregner TI-89, samt med det meget udbredte regneark Excel.
Endvidere er der i et afsnit sidst i bogen også angivet hvorledes beregningerne kan udføres med
lommeregneren TI-83 og matematikprogrammerne Maple og Mathcad.
I 8- udgave findes tabeller over de sædvanlige statistiske funktioner, samt forklaret hvordan
tabellerne anvendes
I denne 11. udgave er der ingen statistiske tabeller, men alle eksempler regnes med anvendelse af
lommeregneren TI89 og regnearkprogrammet Excel.
Endvidere er der indsat et kapitel om deskriptiv statistik, som viser hvordan man kan anvende Excel
til tegning af histogrammer m.m.
Denne udgave, samt 8 udgave kan sammen med en række andre noter findes på adressen:
www.larsen-net.dk
Jeg vil gerne takke ingeniørdocent L. Brøndum og J. D. Monrad for de mange gode råd gennem
årene.
En særlig tak til lektor Bjarne Hellesen, som dels har skrevet afsnit 11 , dels er kommet med mange
værdifulde kommentarer og bidrag til forbedringer.
august 2010 Mogens Oddershede Larsen
i

INDHOLD
1 INTRODUKTION TIL STATISTIK .......................................... 1
2 DESKRIPTIV STATISTIK
2.1 Kvalitative data ......................................................... 2
2.2 Kvantitative data ........................................................ 4
2.3 Karakteristiske tal....................................................... 7
Opgaver ................................................................. 12
3 KONTINUERT STOKASTISK VARIABEL
3.1 Sandsynlighed......................................................... 15
3.2 Stokastisk variabel ..................................................... 16
3.3 Tæthedsfunktion, middelværdi og spredning for kontinuert stokastisk variabel ...... 17
3.4 Linearkombination af stokastiske variable................................... 21
3.5 Usikkerhedsberegning .................................................. 23
Opgaver ................................................................. 26
4 NORMALFORDELINGEN
4.1 Indledning ........................................................... 28
4.2 Definition og sætninger om normalfordeling ................................. 29
4.3 Beregning af sandsynligheder ............................................ 32
Opgaver ................................................................. 36
5 STIKPRØVER
5.1 Udtagning af stikprøver ................................................... 38
5.2 Fordeling og spredning ag gennemsnit ..................................... 39
5.3 Konfidensinterval for middelværdi .......................................... 40
5.3.1 Definition af konfidensinterval ........................................ 40
5.3.2 Populationens spredning kendt eksakt .................................. 41
5.3.3 Populationens spredning ikke kendt eksakt .............................. 43
5.4 Konfidensinterval for spredning ............................................ 48
5.5 Oversigt over centrale formler i kapitel 5 ..................................... 50
Opgaver ................................................................. 51
6 HYPOTESETESTNING (1 NORMALFORDELT VARIABEL)
6.1 Grundlæggende begreber ................................................ 53
6.2 Eksempler på hypotesetest regnet med TI89 og Excel ......................... 56
6.3 Fejl af type I og typr II .................................................. 59
6.4 Oversigt over centrale formler i kapitel 6 ..................................... 63
Opgaver ................................................................. 66
7 HYPOTESETESTNING (2 NORMALFORDELTE VARIABLE)
7.1 Indledning ........................................................... 70
7.2 Sammenligning af 2 normalfordelte variable ................................. 71
7.3 Oversigt over centrale formler i kapitel 7 ..................................... 76
Opgaver ................................................................. 77
ii

Indhold
8 REGNEREGLER FOR SANDSYNLIGHED, KOMBINATORIK
8.1 Regneregler for sandsynlighed ............................................ 80
8.2 Betinget sandsynlighed ................................................. 82
8.3 Kombinatorik ......................................................... 84
8.3.1 Indledning ........................................................ 84
8.3.2 Multiplikationsprincippet ............................................ 84
8.3.3 Ordnet stikprøveudtagelse ............................................ 85
8.3.4 Uordnet stikprøveudtagelse ........................................... 86
Opgaver ................................................................. 88
9 VIGTIGE DISKRETE FORDELINGER
9.1 Indledning ........................................................... 91
9.2 Hypergeometrisk fordeling .............................................. 91
9.3 Binomialfordeling ..................................................... 94
9.4 Poissonfordeling ...................................................... 100
9.5 Den generaliserede hypergeometriske fordeling ............................. 103
9.6 Polynomialfordeling ................................................... 104
9.7 Approksimationer ..................................................... 104
9.8 Oversigt over centrale formler i kapitel 9 ................................... 105
Opgaver ................................................................ 107
10 ANDRE KONTINUERTE FORDELINGER
10.1 Indledning .......................................................... 113
10.2 Den rektangulære fordeling ............................................. 113
10.3 Eksponentialfordelingen .............................................. 115
10.4 Weibullfordelingen ................................................. 117
10.5 Den logaritmiske fordeling ............................................. 118
10.6 Den todimensionale normalfordeling ...................................... 118
Opgaver ................................................................ 119
11 FLERDIMENSIONAL STATISTISK VARIABEL
11.1 Essens ............................................................. 120
11.2 Indledning ......................................................... 121
11.2 Kovarians og korrelationskoefficient ..................................... 123
11.3 Linearkombination ................................................... 126
Opgaver ................................................................ 128
STATISTISKE BEREGNINGER UDFØRT PÅ LOMMEREGNER OG PC
TI-89................................................................... 131
Excel................................................................... 133
TI-83................................................................... 136
Maple .................................................................. 138
Mathcad ................................................................ 139
APPENDIX. OVERSIGT OVER APPROKSIMATIONER ....................... 141
iii

TABEL OVER FRAKTILER I NORMERET NORMALFORDELING ............. 143
FACITLISTE .............................................................. 144
STIKORD ................................................................. 148
iv

1
1 Introduktion til statistik
1 INTRODUKTION TIL STATISTIK
Ved næsten alle ingeniørmæssige problemer vil de indsamlede data udvise variation. Måler man
således gentagne gange indholdet (i %) af et bestemt stof i et levnedsmiddel, vil det procentvise
indhold ikke blive præcis samme tal for hver gang man foretager en måling. Dette kunne naturligvis
være en usikkerhed ved målemetoden, men det vil sjældent være den væsentligste årsag.
Ved mange industrielle processer vil en række ukontrollable forhold indvirke på det endelige
resultat. Eksempelvis vil udbyttet af en kemisk proces variere fra dag til dag, fordi man ikke har
fuldstændig kontrol over forsøgsbetingelser som temperatur, omrøringstid, tidspunkt for
tilsætning af råmaterialer, fugtighed osv. Endvidere er forsøgsmaterialerne muligvis ikke
homogene nok. Råmaterialerne kan f.eks. være af varierende kvalitet, der må bruges forskelligt
apparatur under produktionsprocessen, forskelligt personale deltager i arbejdet osv.
Statistik drejer sig om at samle, præsentere og analysere data med henblik på at foretage
beslutninger og løse problemer.
I den deskriptive statistik beskrives data ved tabeller, grafisk (lagkagediagrammer, søjlediagrammer)
og ved beregning af karakteristiske tal såsom gennemsnit og spredning.
Man kan eksempelvis i “Danmarks Statistik” (findes på nettet under adressen www.statistikbanken.dk
) finde, hvor mange personbiler der er i Danmark i 2009 opdelt efter alder.
Man kender her populationen (biler i Danmark), kan grafisk vise deres fordeling i et søjlediagram
og beregne deres gennemsnitlige alder.
I den mere analyserende statistik (kaldet inferentiel statistik) søger man ved mere avancerede
statistiske metoder ud fra en repræsentativ stikprøve at konkludere noget om hele populationen.
Eksempelvis udtages ved en meningsmåling en forhåbentlig repræsentativ stikprøve på 1000
vælgere, som man spørger om hvilket politisk parti de ville stemme på, hvis der var valg i
morgen.
Man vil så ud fra stikprøven konkludere, at hvis man spurgte hele populationen (alle vælgere i
Danmark) , så ville man med en vis usikkerhed få samme resultat.
Viser stikprøven, at partiet “Venstre” vil gå 2.5% tilbage, så vil det samme ske, hvis der var valg
i morgen.
Et sådant tal er naturligvis usikkert. Man må derfor anvende passende statistiske metoder til
eksempelvis at beregne, at usikkerheden er på 2%.

2 Deskriptiv statistik
2. DESKRIPTIV STATISTIK
I den deskriptive statistik (eller beskrivende statistik) beskrives de indsamlede data i form af
tabeller, søjlediagrammer, lagkagediagrammer, kurver samt ved udregning af centrale tal som
gennemsnit, typetal, spredning osv.
Kurver og diagrammer forstås lettere og mere umiddelbart end kolonner af tal i en tabel. Øjet er
uovertruffet til mønstergenkendelse (“en tegning siger mere end 1000 ord”).
2.1 KVALITATIVE DATA
Hvis der er en naturlig opdeling af talmaterialet i klasser eller kategorier siges, at man har
kategorisk eller kvalitative data .
Alle spørgeskemaundersøgelser, hvor man eksempelvis bliver bedt om at sætte kryds i nogle
rubrikker “meget god” , god, acceptabel osv. er af denne type.
De følgende 2 eksempler viser anvendelse af henholdsvis lagkagediagram og søjlediagram
Eksempel 2.1 Lagkagediagram
Nedenfor er angivet hvordan en kommunes udgifter fordeler sig på de forskellige områder.
Udligning 23,1
øvrige 8,4
Socialområdet,øvrige 9,4
Ældre 18,6
Børnepasning 10,4
Bibliotek 1,9
fritid 3,8
Skoler 10,5
Administration 7,3
Teknik,anlæg 6,6
Dan et lagkagediagram til anskueliggørelse heraf.
Løsning:
Data opskrives i Excel og der gives følgende “ordrer”
2003: Marker udskriftsområde Vælg på værktøjslinien “Guiden diagram” Cirkel Marker ønsket figur Næste Navn
på kategori Udfør
2007: Marker udskriftsområde Vælg på værktøjslinien “Indsæt” Cirkel Marker ønsket figur
Ønskes tekst placeret som på figur
Cursor på figur Formater dataetiketter Vælg “kategorinavn” og “udenfor”.
Skoler
Fritid
kultur
Børnepasning
Administr.
Teknik
Udgifter
Ældre
2
Æ
udligning
Øvrige
socialområdetøvrige

3
2.1 Kvalitative data
Eksempel 2.2 (kvalitative data)
Følgende tabel angiver mandattallet ved de to sidste folketingsvalg.
Partier A B C F K O V Ø
Mandater 2001 52 9 16 12 4 22 56 4
2005 47 17 18 11 0 24 52 6
A = Socialdemokraterne, B =Radikale venstre, C = Konservative folkeparti , F =Socialistisk
folkeparti, K = Kristendemokraterne,
O = Dansk Folkeparti, V = Venstre, Ø = Enhedslisten
Anskueliggør disse mandattal ved i Excel at tegne et søjlediagram
Løsning:
Et søjlediagram fås i Excel ved at opskrive
A B C F K O V Ø
52 9 16 12 4 22 56 4
47 17 18 11 0 24 52 6
2003: Vælg på værktøjslinien “Guiden diagram” Søjle Marker ønsket figur Næste marker udskriftsområde
Næste Næste Udfør
2007: Marker udskriftområde Vælg på værktøjslinien “Indsæt” Søjle Marker ønsket figur
Cursor på vandret akse, højre musetast data Under “rediger kategoriakse” marker bogstavrækken
60
50
40
30
20
10
0
A B C F K O V Ø
Fordelen ved en grafisk fremstilling er, at de væsentligste egenskaber ved data opnås hurtigt og
sikkert. Men netop det, at figurer appellerer umiddelbart til os, gør at vi kan komme til at lægge
mere i dem, end det som tallene egentlig kan bære. Eksempelvis viser forsøg, at i lagkagediagrammer,
hvor man skal sammenligne vinkler (eller arealer), da vil denne sammenligning
afhænge noget af i hvilken retning vinklens ben peger.
Nedenstående eksempel viser hvordan en figur kan være misvisende uden direkte at være forkert.
Serie1
Serie2

2 Deskriptiv statistik
Eksempel 2.3. Misvisende figur
Tønderne i figuren nedenfor skal illustrere hvordan osteeksporten fordeler sig på de forskellige
verdensdele. Den giver imidlertid et helt forkert indtryk. Det er højderne på tønderne der angiver
de korrekte forhold, men af tegningen vil man tro, at det er rumfangene af tønderne. De 3 små
tønder kan umiddelbart være flere gange indeni den store tønde, men det svarer jo ikke til
talforholdene.
De mest almindelige figurer til at give et visuelt overblik over større talmaterialer er histogrammer
(søjlediagrammer) og kurver i et koordinatsystem.
2.2. KVANTITATIVE DATA (VARIABLE)
Kvantitative data er data, hvor registreringen i sig selv er tal, der angiver en bestemt rækkefølge,
f. eks. som i eksempel 1.4 hvor data registreres efter det tidspunkt hvor registreringen foregår
eller som i eksempel 1.5, hvor det er størrelsen af registrerede værdi der er af interesse.
Eksempel 2.4. Kvantitativ variabel: tid
Fra “statistikbanken (adresse http://www.statistikbanken.dk/) er hentet følgende data ind i Excel,
der beskriver hvorledes indvandringer og udvandringer er sket gennem tiden.
Excel: Vælg “Befolkning og valg” Ind- og udvandring Ind- og udvandring på måned under “bevægelse” vælges
alle og under “måned” vælges år og derefter alle Tryk på tabel Drej tabel med uret Gem som Excel fil
Indvandringer og udvandringer efter tid og bevægelseIndvandrede
Udvandrede
1983 27718 25999
1984 29035 25053
1985 36214 26715
1986 38932 27928
1987 36296 30123
1988 35051 34544
1989 38391 34949
1990 40715 32383
1991 43567 32629
1992 43377 31915
1993 43400 32344
1994 44961 34710
1995 63187 34630
1996 54445 37312
1997 50105 38393
1998 51372 40340
1999 50236 41340
2000 52915 43417
2001 55984 43980
2002 52778 43481
2003 49754 43466
2004 49860 45017
2005 52458 45869
2006 56750 46786
2007 64656 41566
2008 72749 43490
2009 67161 44874
Giv en grafisk beskrivelse af disse data.
4

5
2.2 Kvantitative data
Løsning:
Da dataene er registreret efter tid (år) (den kvantitative variabel “tid”) tegnes to kurver i samme
koordinatsystem:
Excel:2003: Marker udskriftsområde Vælg på værktøjslinien “Guiden diagram” Kurve Marker ønsket figur
Næste Næste Næste Udfør
Excel 2007:Marker udskriftsområde Vælg på værktøjslinien “ Indsæt” Streg Marker ønsket figur
Der er foretaget enkelte andre justeringer inden følgende figur fremkom.
80000
70000
60000
50000
40000
30000
20000
10000
0
1983198519871989 1991199319951997199920012003200520072009
Indvandrede
Udvandrede
Eksempel 2.5. Kvantitativ variabel , størrelse af brintionkoncentrationen pH
I menneskers led udskiller den inderste hinde en "ledvæske" som "smører" leddet. For visse
ledsygdomme kan brintionkoncentrationen (pH) i denne væske tænkes at have betydning. Som
led i en nordisk medicinsk undersøgelse af en bestemt ledsygdom udtog man blandt samtlige
patienter der led af denne sygdom en repræsentativ stikprøve ved simpel udvælgelse 75 patienter
og målte pH i ledvæsken i knæet.
Resultaterne (som kan findes som excel-fil på adressen www.larsen-net.dk ) var følgende:
7.02 7.26 7.31 7.16 7.45 7.32 7.21 7.35 7.25 7.24 7.20 7.21 7.27 7.28 7.19
7.39 7.40 7.33 7.32 7.35 7.34 7.41 7.28 7.27 7.28 7.33 7.20 7.15 7.42 7.35
7.38 7.32 7.71 7.34 7.10 7.35 7.15 7.19 7.44 7.12 7.22 7.12 7.37 7.51 7.19
7.30 7.24 7.36 7.09 7.32 6.95 7.35 7.36 7.52 7.29 7.31 7.35 7.40 7.23 7.16
7.26 7.47 7.61 7.23 7.26 7.37 7.16 7.43 7.08 7.56 7.07 7.08 7.17 7.29 7.20
Giv en grafisk beskrivelse af disse data.
Løsning:
I dette tilfælde, hvor vi er interesseret i at få et overblik over tallenes indbyrdes størrelse er det
fordelagtigt at tegne et histogram.
Et histogram ligner et søjlediagram, men her gælder, at antallet af enheder i hver søjle repræsenteres
ved søjlens areal (histo er græsk for areal). Man bør så vidt muligt sørge for at grupperne
er lige brede, da antallet af enheder så svarer til højden af søjlen.
Excel kan umiddelbart tegne er histogram, men af hensyn til det følgende forklares hvordan man
bestemmer intervalopdeling m.m.
Først findes det største tal x max og det mindste tal x min i materialet og derefter beregne variationsbredden
x max - x min. Vi ser, at største tal er 7.71 og mindste tal er 6.95 og variationsbredden
derfor 7.71 - 6.95 = 0.76.

2 Deskriptiv statistik
Dernæst deles tallene op i et passende antal intervaller (klasser). Som det første bud vælges ofte
et antal nær n . Da
076 .
75 ≈ 9 vælges ca. 9 klasser. Da ≈ 008 . deler vi op i de klasser, der
9
ses af tabellen. Dette giver 10 intervaller. Vi tæller op hvor mange tal der ligger i hvert interval
(gøres nemmest ved at starte forfra og sæt en streg i det interval som tallet tilhører).
Klasser Antal n
]6.94 - 7.02] // 2
]7.02 - 7.10] ///// 5
]7.10 - 7.18] //////// 8
]7.18 - 7.26] ///////////////// 17
]7.26 - 7.34] ////////////////// 18
]7.34 - 7.42] //////////////// 16
]7.42 - 7.50] //// 4
]7.50 - 7.58] /// 3
]7.58 - 7.66] / 1
]7.66 - 7.74] / 1
Allerede her kan man se, at antallet er størst omkring 7.30, og så falder hyppigheden nogenlunde
symmetrisk til begge sider.
I Excel sker det på følgende måde:
Data indtastes i eksempelvis søjle A1 til A75 ( data findes på adressen www.larsen-net.dk )
2003: Vælg “Funktioner” Dataanalyse Histogram
2007: Vælg “Data” Dataanalyse Histogram
I den fremkomne tabel udfyldes “inputområdet” med A1:A75 og man vælger “diagramoutput”..
1) Trykkes på OK fås en tabel med hyppigheder, og en figur, hvor intervalgrænserne er fastlagt af Excel.
2) Ønsker man selv at bestemme grænserne, skal man også udfylde intervalområdet. Dette gøres ved at skrive de
øvre grænser i en søjle (f.eks. i B1 6.94, i B2 7.02 osv. til B10: 7.66) og så skrive B1:B10 i inputområdet
Nedenstående figurer er blevet gjort lidt “pænere” ved
cursor på en søjle tryk højre musetast formater dataserie indstilling mellemrumsbredde = 0 ok
I tilfælde 1 fremkommer så følgende udskrift og tegning:
Interval Hyppighed
6,95 1
7,045 1
7,14 7
7,235 17
7,33 22
7,425 18
7,52 6
7,615 2
Mere 1
25
20
15
10
5
0
6
Hyppighed
6,95 7,045 7,14 7,235 7,33 7,425 7,52 7,615 Mere
Hyppighed

I tilfælde 2 følgende
Interval Hyppighed
6,94 0
7,02 2
7,1 5
7,18 8
7,26 17
7,34 18
7,42 16
7,5 4
7,58 3
7,66 1
Mere 1
7
2.3 Karakteristiske tal
Histogrammet er et "klokkeformet histogram", hvor der er flest tal fra 7.19 til 7.42, og derefter
falder antallet til begge sider.
Man regner normalt med, at resultaterne af forsøg, hvor man har foretaget målinger (hvis man
lavede nok af dem) har et sådant klokkeformet histogram og siger, at resultaterne er normalfordelt
(beskrives nærmere i næste kapitel)
2.3 KARAKTERISTISKE TAL
20
18
16
14
12
10
8
6
4
2
0
Hyppighed
6,94 7,02 7,1 7,18 7,26 7,34 7,42 7,5 7,58 7,66 Mere
Skal man sammenligne to talmaterialer, eksempelvis sammenligne de 75 pH-værdier i eksempel
1.4 med 200 dårlige knæ fra Tyskland, har det ingen mening at sammenligne hyppighederne
Man må i sådanne tilfælde angive nogle tal, som gør det muligt at foretage en sammenligning.
Dette kunne blandt andet ske ved at man udregnede de relative hyppigheder
2.3.1 Relativ hyppighed
Ved den relative hyppighed forstås hyppigheden divideret med det totale antal.
I eksempel 2.5 er den relative hyppighed for pH - værdier i intervallet ]7.18 - 7.26]:
17
= 02267 . = 2257% .
75
Man kunne sige, at “sandsynligheden” er 22.57% for at pH ligger i dette interval.
Hyppighed
2.3.2 Middelværdi
Kendes hele “populationen” (målt højden på alle danske mænd) kan beregnes en “korrekt midterværdi”
kaldet middelværdi µ (græsk my)
Ud fra stikprøven vil en tilnærmet værdi (kaldet et estimat) for µ være gennemsnittet x (kaldt
x streg).
x1 + x2 + ... + xn
Kaldes observationerne i en stikprøve x1, x2,..., xner x =
n

2 Deskriptiv statistik
Eksempel 2.6: Gennemsnit
Find gennemsnittet af tallene 6, 17, 7, 13, 5, 3
Løsning: x = + + + + + 6 17 7 13 5 3
= 85 .
6
TI 89: Catalog mean ({6, 17, 7, 13, 5, 3}) .
Excel: Tast tallene i en kolonne eksempelvis A1 til A6 Vælg på værktøjslinien fx Middel( A1..A6)
2.3.3 Median:
Medianen beregnes på følgende måde:
1) Observationerne ordnes i rækkefølge efter størrelse.
2a) Ved et ulige antal observationer er medianen det midterste tal
2b) Ved et lige antal er medianen gennemsnittet af de to midterste tal.
Eksempel 2.7: Median
Find medianen af tallene 6, 17, 7, 13, 5, 3.
Løsning: Ordnet i rækkefølge: 3, 5, 6, 7 13, 17. Median 6,5
TI 89: Catalog median ({ 6, 17, 7, 13, 5, 2}) .
Excel: Tast tallene i en kolonne eksempelvis A1 til A6 Vælg fx Median( A1..A6)
Medianen kaldes også for 50% fraktilen, fordi den brøkdel (fraktil) der ligger under medianen
er ca. 50% .
Er median og gennemsnit nogenlunde lige store fordeler tallene sig nogenlunde symmetrisk
omkring middelværdien.
Er medianen mindre end gennemsnittet er der muligvis tale om
en “højreskæv” fordeling som har den “lange” hale til højre.(se
figuren)
Er medianen større end gennemsnittet, er der muligvis tale om en
venstreskæv fordeling
At man eksempelvis i lønstatistikker 1 angives medianen og ikke
gennemsnittet fremgår af følgende lille eksempel.
Lad os antage at en virksomhed har 10 ansatte, med månedslønninger ordnet efter størrelse på
20000, 21000, 22000, 23000, 24000, 25000, 26000, 27000, 28000, 100000
Gennemsnittet er her 31600, mens medianen er 24500.
Medianen ændrer sig ikke selv om den højeste løn vokser fra 100000 til 1 million, mens gennemsnittet
naturligvis vokser. Medianen giver derfor en mere rimelig beskrivelse af middellønnen i
firmaet.
I nævnte lønstatistik er også angivet “nedre og øvre Kvartil” som er det tal som henholdsvis 25%
og 75% af tallene ligger under.
Nedre og øvre kvartil kaldes også 25% fraktil og 75% fraktil.
1
jævnfør statistisk årbog 2005 tabel 144 eller se www.statistikbanken.dk Og vælg løn\lønstatistik for den statslige
sektor\løn32\klik for at vælge\alle værdier\hovedgrupper\ledelse på højt niveau+kontorarbejde
8

Ved at angive dem får man et indtryk af, hvor stor lønspredningen er.
9
2.3 Karakteristiske tal
2.3.4 Spredningsmål
Egentlige målefejl, såsom at nogle af observationerne ikke bliver korrekt registreret, uklarheder
i spørgeskemaet osv. skal naturligvis fjernes.
Derudover er der den “naturlige” variation som også kunne kaldes “ren støj” (pure error), som
skyldes, at man ikke kan forvente, at to personer der på alle områder er stillet fuldstændigt ens
også vil svare ens på et spørgsmål. Tilsvarende hvis man måler udbyttet ved en kemisk proces,
så vil udfaldet af to forsøg ikke være ens, da der altid er en række ukontrollable støjkilder
(urenheder i råmaterialer, lidt forskel på personer og apparatur osv.)
Denne naturlige variation skal naturligvis inddrages i den statistiske behandling af problemet,
og dertil spiller et mål for, hvor meget tallene spreder sig naturligvis en væsentlig rolle..
2.3.4.1 Spredning (engelsk: standard deviation)
Hvis spredningen baserer sig på hele populationen benævnes den σ (sigma) .
Baserer spredningen sig kun på en stikprøve benævnes den s.
Man siger, at s er et estimat (skøn) for σ .
n
∑
( )2
s beregnes af formlen s =
i=
1
xi−x n −1
hvor observationerne i en stikprøve er
Varians er s .
2
Eksempel 2.8: Spredning
Find varians og spredning af tallene 6, 17, 7, 13, 5, 3
Løsning:
I eksempel 2.6 findes gennemsnittet x = 85 .
Variansen s 2 ( 6− 85 . ) + ( 17− 85 . ) + ( 7− 85 . ) + ( 13− 85 . ) + ( 5− 85 . ) + ( 3−85 . )
=
6−1 Spredningen s = =
28 7 5357
. .
TI 89: Catalog Variance ({6, 17, 7, 13, 5, 3}),
Catalog stdDev ({6, 17, 7, 13, 5, 3})
Excel: Tast tallene i en kolonne eksempelvis A1 til A6,
vælg fx Varians( A1..A6)
vælg fx STDDEV( A1..A6)
2 2 2 2 2 2
x1, x2,..., xn = 28. 7

2 Deskriptiv statistik
Anskuelig forklaring på formlen for s.
At formlen for s skulle være særlig velegnet til at angive, hvor meget resultaterne “spreder sig” (hvor megen støj der
er ) er ikke umiddelbart indlysende. I det følgende gives en anskuelig forklaring.
Lad os betragte 2 forsøgsvariable X og Y, hvorpå der for hver er udført en stikprøve på 4 forsøg.
Resultaterne var: X: 35.9, 33.3, 34.7, 34.1 med gennemsnittet x = 34.5 , og
Y: 34.3, 34.6, 34.7, 34.4 med gennemsnittet y = 34.5.
De to forsøgsvariable har samme gennemsnit, men det er klart, at Y-resultaterne grupperer sig meget tættere om
gennemsnittet end X-resultaterne, dvs. Y-stikprøven har mindre spredning (der er mindre støj på Y - forsøget) end Xstikprøven.
For at få et mål for stikprøvens spredning beregnes resultaternes afvigelser fra gennemsnittet.
xi−x y y
10
i −
35.9 - 34.5 = 1.4 34.3 - 34.5 = - 0.2
33.3 -34.5 = - 1.2 34.6 - 34.5 = 0.1
34.7 - 34.5 = 0.2 34.7 - 34.5 = 0.2
34.1 - 34.5 = - 0.4 34.4 - 34.5 = -0.1
Summen af disse afvigelser er naturligvis altid 0 og kan derfor ikke bruges som et mål for stikprøvens spredning.
I stedet betragtes summen af kvadraterne på afvigelserne (forkortet SS: Sum of Squares eller SAK: Sum af afvigelsernes
Kvadrat).
n
∑
2 2 2 2 2
SAK = ( x − x)
= 14 . + ( − 12 . ) + 02 . + ( − 04 . ) = 360 .
x i
i=
1
n
∑
2 2 2 2 2
SAK = ( y − y)
= ( − 02 . ) + 01 . + 02 . + ( − 01 . ) = 010 .
y i
i=
1
Da et mål for variansen ikke må være afhængig af antallet af forsøg, divideres med n - 1.
Umiddelbart ville det være mere rimeligt at dividere med n. Imidlertid kan det vises, at i middel bliver et skøn for
variansen for lille, hvis man dividerer med n, mens den “rammer” præcist, hvis man dividerer med n - 1. Det kan
forklares ved, at tallene xi har en tendens til at ligge tættere ved deres gennemsnit x end ved middelværdien µ .
2 360
sx . og
4 1 12 = − =
.
2 01 .
. sy = = 0. 0333 sx = 12 . = 1095 . sy = 0. 0333 = 0183 .
4− 1
Som vi forudså, er stikprøvens spredning betydelig større for X-resultaterne end for Y-resultaterne.
Frihedsgrader. Man siger, at stikprøvens varians er baseret på f = n - 1 frihedsgrader. Navnet
skyldes, at kun n -1 af de n led xix kan vælges frit, idet summen af de n led er nul. Eksempel-
−
vis ser vi af ovenstående eksempel, at der er 3 frihedsgrader, da kendskab til de første 3 led på
1.4, -1.2 og 0.2 er nok til at bestemme det fjerde led, da summen er nul.
Vurdering af størrelsen af stikprøvens spredning.
Man kan vise, at for tæthedsfunktioner med kun et maksimumspunkt gælder, at mellem x − 2⋅
s
og x + 2⋅s
ligger ca. 89% af resultaterne, og mellem
x −3⋅s og x + 3⋅sligger
ca. 95% af resultaterne.
For såkaldte normalfordelte resultater, er de tilsvarende tal ca. 95% og 99.7 %

1
jævnfør statistisk årbog 2005 tabel 144 eller se www.statistikbanken.dk
under løn\lønstatistik for den offentlige sektor \løn 32
11
2.3 Karakteristiske tal
2.3.4.2 Kvartilafstand:
Hvis fordelingen ikke er rimelig symmetrisk, er medianen det bedste skøn for en midterværdi, og
kvartilafstanden kan være et mål for spredningen.
I den tidligere omtalte lønstatistik 1 findes bl.a. følgende tal, idet de to sidste kolonner er vor
bearbejdning af tallene.
Løn pr. præsteret time
nr gennemsnit x nedre kvartil
k1
median m øvre kvartil
k3
1 Ledelse på højt
niveau
353.41 231.63 313.38 433.78 1.13 0.64
2 Kontorarbejde 196.82 158.86 186.99 222.78 1.05 0.34
x
m
k3−k1 m
x
Af kolonnen ses, at for begge rækker er gennemsnittet større end medianen dvs. begge
m
fordelinger er højreskæv, men det gælder mest for række nr. 1. Her gælder åbenbart, at nogle få
forholdsvis høje lønninger trækker gennemsnittet op.
Skal man sammenligne lønspredningen i de to tilfælde, må man tage hensyn til, at medianen er
meget forskellig. Man vil derfor som der er sket i sidste kolonne beregne den relative kvartilafstand.
Den viser også, at lønspredningen er væsentlig mindre for række 2 end for række 1 .
Eksempel 2.9 Kvartil
Find kvartiler og median af de 12 tal 7 , 9 , 11, 3 , 16, 12, 15, 8, 2, 18, 22, 10
Løsning:
TI89:APPS Stat/List Indtast tal i en liste F4 1-Var Stats Angiv listens navn Enter
Blandt mange tal fås 1 kvartil 7.5 og 3 kvartil 15.5
Excel: 2003 og 2007: Data indtastes i eksempelvis søjle A1 til A12 På værktøjslinien foroven:
f x
Der fremkommer en tabel med anvisning på, hvordan den skal udfyldes
Resultat : 1. kvartil 7.75 3 kvartil 15.25
Tryk på = På rullemenu vælges “Kvartil” (evt. først vælg kategorien “statistik”)
Ligesom man på TI 89 kan få mange karakteristiske tal på en gang ved at vælge “1-Var Stats” har
Excel en tilsvarende menu.
Excel: 2003: Funktioner Dataanalyse Beskrivende statistik udfyld inputområde Resumestatistik
2007: Data Dataanalyse Beskrivende statistik udfyld inputområde Resumestatistik

2 Deskriptiv statistik
OPGAVER
Opgave 2.1.
I www.statistikbanken.dk/luft4 er følgende oplysninger for året 2003 hentet ind i Excel.
Udslip til luft af drivhusgasser efter enhed, type, kilde og tid
2003
Mia. C02-ækvivalenter I alt Energisektoren 32
Industri og produktion 8
Transport 13
Affaldsbehandling 2
Landbrug 10
Andet 9
a) Hent selv disse data ind i Excel, og opstil et lagkagediagram til belysning af tallene.
b) Find de tilsvarende tal for 1996, og vælg en passende grafisk fremstilling til sammenligning
af tallene fra 1996 og 2003.
c) Beregn i Excel for årene 1990 til 2003 energisektorens udslip i forhold til det samlede udslip
af drivhusgasser (i %), og tegn dette grafisk.
Opgave 2.2
Følgende tabel angiver for et udvalgt antal lande oplysning om middellevetid for befolkningen
og indbyggerantal.
Land Middellevetid Indbyggertal i millioner
Australien 80.3 19.9
Canada 80.0 32.5
Danmark 77,5 5.5
Frankrig 79.4 60.4
Marokko 70.4 32.2
Polen 74.2 38.6
Sri Lanka 72.9 19.9
USA 77.4 293.0
1) Indskriv ovenstående tabel i Excel, hvor landene er opskrevet alfabetisk.
Benyt Excel til
1) at ordne landene efter middellevetid (længst levetid først), og afbild dem grafisk.
2) tegn i et koordinatsystem to kurver, som angiver såvel landenes størrelse som middellevetid
Opgave 2.3
I http://www.statistikbanken.dk/statbank5a/default.asp?w=1600 findes nogle oplysninger om
Danmarks forbrug af energi efter type og mængde.
1) Hent produktion af naturgas og råolie ind målt i tons for de sidste 2 år (i måneder) ind i Excel
2) Tegn i Excel i samme koordinatsystem to kurver for henholdsvis produktionen af naturgas og
råolie.
12

13
Opgaver til kapitel 2
Opgave 2.4
Færdselspolitiet overvejede, om der burde indføres en fartgrænse på 70 km/h på en bestemt
landevejsstrækning, hvor der hidtil havde været en fartgrænse på 80 km/h.
Som et led i analysen af hensigtmæssigheden af den overvejede ændring observeredes inden for
et bestemt tidsrum ved hjælp af radarkontrol de forbipasserende bilers fart.
Resultatet af målingerne (som kan findes som excel-fil på adressen www.larsen-net.dk ) var:
50 observationer
64
50
59
75
98
72
63
49
74
55
82
35
55
64
85
52
60
99
74
80
60
77
65
62
78
1) Foretag en vurdering af, om fordelingen er nogenlunde symmetrisk (normalfordelt) ved
a) at tegne et histogram
b) at beregne karakteristiske værdier
2) Angiv hvor stor en procent af bilisterne, der “approksimativt” overstiger hastighedsgrænsen
på 80 km/h. (Vink: Anvend histogram og kumulativ frekvens samt hensigtsmæssige intervalgrænser).
Opgave 2.5
Til fabrikation af herreskjorter benyttes et råmateriale, som indeholder en vis procentdel uld. For
nærmere at undersøge uldprocenten, måles denne i 64 tilfældigt udvalgte batch.
Resultatet (som kan findes som excel-fil på adressen www.larsen-net.dk ) var (i %):
34.2 33.1 34.5 35.6 36.3 35.1 34.7 33.6 33.6 34.7 35.0 35.4 36.2 36.8 35.1 35.3
95
41
76
70
53
33.8 34.2 33.4 34.7 34.6 35.2 35.0 34.9 34.7 33.6 32.5 34.1 35.1 36.8 37.9 36.4
37.8 36.6 35.4 34.6 33.8 37.1 34.0 34.1 32.6 33.1 34.6 35.9 34.7 33.6 32.9 33.5
35.8 37.6 37.3 34.6 35.5 32.8 32.1 34.5 34.6 33.6 24.1 34.7 35.7 36.8 34.3 32.7
1) Foretag en vurdering af, om fordelingen er nogenlunde symmetrisk (normalfordelt) ved
a) at tegne et histogram
b) at beregne karakteristiske værdier
Der er i datamaterialet en såkaldte outliers (en mulig fejlmåling). En sådan kan ødelægge
enhver analyse. Det er i dette tilfælde tilladeligt at fjerne den, da vi går ud fra det er en fejlmåling.
2) Beregn stikprøvens relative kvartilafstand
86
47
76
85
96
70
88
68
73
71
63
62
51
93
84
48
66
80
65
103

2 Deskriptiv statistik
Opgave 2.6
Den følgende tabel (som kan findes som excel-fil på adressen www.larsen-net.dk ) viser vægtene
(i kg) af 80 kaniner.
2.90
2.60
2.45
2.75
2.60
2.55
2.45
2.70
2.75
2.80
2.95
2.65
2.65
2.85
2.45
2,70
3.15
2.95
2.70
2.95
3.20
3.40
2.80
2.95
2.65
2.75
2.90
2.85
2.75
2.90
3.20
3.00
2.70
2.70
2.95
2.85
2.50
2.95
2.65
2.90
2.60
2.95
3.05
3.05
2.95
14
2.90
3.00
2.65
2.90
2.75
2.85
3.25
2.70
3.00
2.75
2.70
2.80
2.70
2.75
2.80
2.80
2.70
3.00
2.60
3.00
2.55
2.60
2.80
3.00
2.50
3.10
2.80
2.70
3.15
3.00
1) Foretag en vurdering af, om fordelingen er nogenlunde symmetrisk (normalfordelt) ved
a) at tegne et histogram
b) at beregne karakteristiske værdier
2) Angiv hvor stor en procent af kaninerne, der “approksimativt” overstiger en vægt på 3 kg
(Vink: Anvend histogram og kumulativ frekvens).
2.90
2.70
3.00
2.60
3.15
Opgave 2.7
I “statistikbanken” finder man under punktet “Uddannelse og kultur”,”Fuldførte kompetancegivende
uddannelser ved bacheloruddannelserne” en statistik over antal elever i “Maskinteknik”
og “Design og Innovation” i 2008 fordelt efter alder fra 20 til 36 år for hele landet.
1) Indsæt data i Excel for de to uddannelser.
2) Lav et søjlediagram over aldersfordelingen for de to uddannelser
3) Beregn på basis af ovennævnte tal den gennemsnitlige alder af de studerende for de to uddannelser
i.
Opgave 2.8
I “statistikbanken” find under Løn ,fortjeneste for privatansatte efteruddannelse osv., Højere
uddannelse, Teknisk, ledere i 2008
“Gennemsnit, median, øvre og nedre kvartil for såvel mænd som kvinder “
1) Overfør data til Excel på egen harddisk
2) Angiv om de to fordelinger er symmetrisk, højre eller venstreskæv
3) Er der forskel på lønspredningen for mænd og kvinder
(Vink: Beregn den relative kvartilafstand)

15
3.1 Sandsynlighed
3 KONTINUERT STOKASTISK VARIABEL
3.1 SANDSYNLIGHED
Statistik bygger på sandsynlighedsteorien, som giver metoder til at finde, hvor stor chancen
(sandsynligheden) er for at et bestemt resultat af et eksperiment forekommer.
DEFINITION af tilfældigt eksperiment. Et eksperiment som kan resultere i forskellige
udfald, selv om eksperimentet gentages på samme måde hver gang, kaldes et tilfældigt
eksperiment (engelsk : random experiment).
Det er karakteristisk for tilfældige eksperimenter, at man kan afgrænse en mængde kaldet
eksperimentets udfaldsrum U, der indeholder de mulige udfald. Derimod kan man ikke forudsige,
hvilket udfald der vil indtræffe ved udførelsen af eksperimentet.
Består eksperimentet eksempelvis i kast med en terning er udfaldsrummet U = {1, 2, 3, 4 ,5, 6},
men man kan ikke forudsige udfaldet af næste kast (eksperiment). Selv om man 4 gange i træk
har fået udfaldet “øjental 1", kan man ikke forudsige, hvilket udfald der indtræffer næste gang.
Resultatet af 5. kast afhænger ikke af resultaterne af de foregående 4 spil. Man siger, at eksperimenterne
er "statistisk uafhængige" (en præcis definition ses i kapitel 9).
Som eksempler på tilfældige eksperimenter kan nævnes:
a) Ét kast med en mønt. Udfaldsrum U = Plat, Krone .
{ }
b) Fremstilling af et parti levnedsmiddel og måling af det procentvise indhold af protein.
U = mængden af reelle tal fra 0 til 100.
c) Udtage en stikprøve på 400 elektroniske komponenter af en dagsproduktion og optælling af
0, 1, 2, 3, 4, 5,..., 400
antallet af defekte komponenter. U = { }
d) Udtagning af et tilfældigt TV-apparat fra en dagsproduktion af TV-apparater og optælling af
antallet af loddefejl. U = mængden af positive hele tal.
En hændelse er en delmængde af et eksperiments udfaldsrum.
Eksempelvis er A: “At få et lige øjental” en hændelse ved kast med en terning.
Hændelsen A siges at indtræffe, hvis et udfald fra A forekommer.
Sandsynlighedsbegrebet tager udgangspunkt i det i kapitel 1 omtalte begreb “relativ hyppighed”.
DEFINITION af relativ hyppighed for hændelse A. Gentages et eksperiment n gange,
og forekommer hændelsen A netop n A gange af de n gange, er A’s relative
n
hyppighed hA ( )=
n
A

3. Kontinuert stokastisk variabel
Lad eksempelvis eksperimentet være kast med en terning og hændelsen A være at få et lige
øjental. Kastes terningen 100 gange og bliver resultatet et lige øjental 45 af de 100 gange er h(A)
= 0.45.
Det er en erfaring, at øges antallet af gentagelser af eksperimentet, vil den relative hyppighed af
hændelsen A stabilisere sig. Når n går mod ∞ ,vil den relative hyppighed erfaringsmæssigt
nærme sig til en grænseværdi ("de store tals lov").
Ved sandsynligheden for A som benævnes P(A) forstås denne grænseværdi. (P = probability)
Da definitionen af sandsynlighed bygger på relativ hyppighed, er det naturligt, at det for ethvert
par af hændelser A og B i udfaldsrummet U skal gælde :
0≤ P( A)
≤1,
PU ( )= 1 og
P(enten A eller B) = P(A) + P(B) forudsat A og B ingen elementer har fælles (er disjunkte).
Den sidste regel skrives kort P( A∪ B) = P( A) + P( B)
Eksempel 3.1 Anvendelse af regel P( A∪ B) = P( A) + P( B)
Lad A = at få et lige øjental ved kast med en terning
B = at få en sekser ved et kast mad en terning
Find sandsynligheden for enten at få et lige øjental eller en sekser ved kast med en terning.
Løsning:
1 1
1 1 2
P(A) = . P(B) =
P( A∪ B) = P( A) + P( B)
= + =
2 6
2 6 3
De 3 regler kaldes sandsynlighedsregningens aksiomer.
I kapitel 8 udledes på dette grundlag en række regler for regning med sandsynligheder.
3.2 STOKASTISK VARIABEL
Ethvert statistisk problem må det på en eller anden måde være muligt at behandle talmæssigt.
Betragtes et eksempel med kast med en mønt, kunne man til udfaldet plat tilordne tallet 0 og til
udfaldet krone tilordne tallet 1 og på den måde få problemet overført til noget, hvor man kan
foretage beregninger. Man siger, man har indført en stokastisk (eller statistisk) variabel X, som
er 0, når udfaldet er plat, og 1 når udfaldet er krone.
Generelt gælder følgende definition:
DEFINITION af stokastisk variabel (engelsk: random variable). En stokastisk variabel
(også kaldet statistisk variabel) er en funktion, som tilordner et reelt tal til hvert udfald i
udfaldsrummet for et tilfældigt eksperiment.
En stokastisk variabel betegnes med et stort bogstav såsom X, mens det tilsvarende lille bogstav
x betegner en mulig værdi af X.
Er eksempelvis eksperimentet “udtagning af en kasse med 100 møtrikker, ud af en løbende
produktion af kasser”, kunne den stokastiske variabel X være defineret som “ antal defekte
møtrikker i kassen”.
16

17
3.3 Tæthedsfunktion
Et andet eksempel kunne være eksperimentet “anvendelse af en ny metode til fremstilling af et
produkt”. Her kunne den stokastiske variabel Y være det målte procentvise udbytte ved forsøget.
Ved en diskret variabel (eller tællevariabel) forstås en variabel, hvis mulige værdier udgør en
endelig eller tællelig mængde.
I eksemplet hvor X er antal defekte møtrikker, er X en diskret variabel, da den kun kan antage
heltallige værdier fra 0 til 100.
Vi vil i senere afsnit behandle diskrete variable.
Ved en kontinuert stokastisk variabel forstås en stokastisk variabel, hvis mulige værdier er alle
reelle tal i et vist interval.
I eksemplet, hvor Y er det målte procentiske udbytte, er Y en kontinuert variabel, da den kan
antage alle værdier fra 0% til 100%.
3.3 TÆTHEDSFUNKTION
Vi vil benytte eksempel 1.5 til illustration.
Eksempel 3.2. Kontinuert stokastisk variabel
I menneskers led udskiller den inderste hinde en "ledvæske" som "smører" leddet. For visse
ledsygdomme kan koncentrationen af brintioner (pH) i denne væske tænkes at have betydning.
Som led i en nordisk medicinsk undersøgelse af en bestemt ledsygdom udtog man blandt samtlige
patienter der led af denne sygdom tilfældigt 75 patienter og målte pH i ledvæsken i knæet.
Resultaterne findes i eksempel 1.5
Population og stikprøve. Samtlige indbyggere i Norden med denne sygdom udgør populationen.
Da det er ganske uoverkommeligt at undersøge alle, udtages en stikprøve på 75 patienter.
Det er målet ved hjælp af statistiske metoder på basis af en stikprøve at sige noget generelt om
populationen.
Histogram. For at få et overblik over et større datamateriale, vil man sædvanligvis starte med
at tegne et histogram. Hvorledes dette gøres fremgår af eksempel 1.5.
I skemaet ses resultatet af en opdeling i 10 klasser med en bredde på 0.08.
Endvidere er der beregnet en søjle ved at dividere den relative hyppighed med intervallængden.
Klasser Antal n Relativ hyppighed
n
75
Skalering
]6.94 - 7.02] 2 0.0267 0.3333
]7.02 - 7.10] 5 0.0667 0.8333
]7.10 - 7.18] 8 0.1067 1.3333
]7.18 - 7.26] 17 0.2267 2.8333
]7.26 - 7.34] 18 0.2400 3.0000
]7.34 - 7.42] 16 0.2133 2.6667
]7.42 - 7.50] 4 0.0533 0.6667
]7.50 - 7.58] 3 0.0400 0.5000
]7.58 - 7.66] 1 0.0133 0.1667
]7.66 - 7.74] 1 0.0133 0.1667
n
75⋅ 0. 08

3. Kontinuert stokastisk variabel
Vi får det nedenfor tegnede histogram (kan ses beregnet i eksempel 1.5)
Dette viser et "klokkeformet histogram", hvor der er flest tal fra 7.19 til 7.42, og derefter falder
antallet til begge sider.
18
15
12
9
6
3
Histogram for pH
0
6,9 7,1 7,3 7,5 7,7 7,9
pH
Man regner normalt med, at resultaterne af forsøg hvor man har foretaget målinger (hvis man
lavede nok af dem) har et sådant klokkeformet histogram. Hvis man tænker sig antallet af forsøg
stiger (for eksempel undersøger hele populationen på måske 1 million nordiske knæ), samtidig
6
med at man øger antallet af klasser tilsvarende (til for eksempel 10 ≈ 1000 ) , vil histogrammet
blive mere og mere fintakket, og til sidst nærme sig til en kontinuert klokkeformet kurve (indtegnet
på grafen).
Hvis man benytter den skalerede skala fra skemaet, som også er afsat på højre side af tegningen,
vil arealet af hver søjle være den relative hyppighed, og for den idealiserede kontinuerte kurve,
vil arealet under kurven i et bestemt interval fra a til b være sandsynligheden for at få en værdi
mellem a og b.
Det samlede areal under kurven er naturligvis 1.
Man siger, at den kontinuerte stokastiske variabel X (pH værdien) har en tæthedsfunktion f(x)
hvis graf er den ovenfor nævnte kontinuerte kurve.
Da arealet under en kontinuert kurve beregnes ved et bestemt integral, følger heraf følgende
definition:
DEFINITION af tæthedsfunktion f(x) for kontinuert variabel X.
Pa ( ≤ X≤ b) = f( xdx ) for ethvert interval af reelle tal
∫ [ a; b]
∞
a
b
∫ f ( x) dx = 1, f ( x)≥0for
alle x
−∞
Bemærk, at for kontinuerte variable er
Pa ( ≤ X≤ b) = Pa ( < X≤ b) = Pa ( ≤ X< b) = Pa ( < X< b).
18

19
3.3 Tæthedsfunktion
Et eksempel på en tæthedsfunktion for en kontinuert variabel er den i næste kapitel beskrevne
normalfordeling.
Måleresultater vil sædvanligvis være værdier af normalfordelte variable, så en rimelig hypotese
for den i eksempel 3.2 angivne kontinuerte stokastiske variabel X = pH er således, at den er
normalfordelt. Dette bestyrkes af at grafen for sådanne netop er klokkeformede .
Det er væsentlig at finde en central værdi i populationen, samt angive et spredningsmål
Disse angives i de følgende kapitler for de konkrete funktioner, der behandles.
Generelt gælder følgende definitioner
DEFINITION af middelværdi for kontinuert variabel. Middelværdi for en kontinuert variabel X med tætheds-
∞
funktion f ( x ) benævnes µ eller E ( X ) og er defineret som µ = E( X) = x⋅ f ( x) dx
DEFINITION af varians og spredning for kontinuert variabel. Variansen for en kontinuert variabel X med
tæthedsfunktion f ( x ) benævnes σ eller V( X ) og er defineret som
2 2
σ = V( X) =
∞
2
( x−µ ) ⋅ f ( x) dx
Spredningen (engelsk: standard deviation) for en diskret variabel X med tæthedsfunktion f(x) benævnes σ og er
defineret som σ = V( X)
Eksempel 3.3 Kontinuert stokastisk variabel.
3 2
⎧⎪
⋅x for 0≤ x<
2
8
Lad der være givet følgende funktion: f ( x)=
⎨
.
⎩⎪ 0 ellers
∫
a) Vis, at f ( x) dx = 1
∞
−∞
I det følgende antages, at f ( x ) er tæthedsfunktion for en kontinuert stokastisk variabel X.
b) Skitser grafen for f.
c) Beregn middelværdi og spredning for X.
Løsning:
x
a) f ( x) dx = x dx = .
⎡ ⎤
⎢ ⎥
⎣ ⎦
=
∞
2
3
3 2
∫−∞ ∫
1
0
8
8
b) Grafen, som er en del af en parabel, ses på Fig 3.1.
c) µ = = ⋅ = ⋅ = .
⎡ ⎤
⎢ ⎥
⎣ ⎦
=
∞
2
4
2
3 2 x 3
E( X) ∫ x f ( x) dx
−∞ ∫ x x dx 3
0 8 32 2
2
0
0
2 5
∫
−∞
∫
−∞
Fig.3.1 Tæthedsfunktion
x
V( X) = x ⋅ f ( x) dx − = x ⋅ x dx − . . . .
⎛ ⎞
⎜ ⎟ =
⎝ ⎠
⎡
∞
2
2 2 2 3 2 3 ⎤
∫ µ ⎢ ⎥ − =
−∞
∫
3 225 015 σ ( X ) = 015 . = 0. 387
0 8 2 ⎣ 40⎦
2
0

3. Kontinuert stokastisk variabel
Fordelingsfunktion. I visse situationer er det en fordel at betragte den kontinuerte variabels fordelingsfunktion F(x)
DEFINITION af fordelingsfunktion F(x) for kontinuert variabel.
x
Fordelingsfunktionen for en kontinuert variabel X er defineret ved F( x) = P( X ≤ x) = ∫ f ( x) dx
−∞
DEFINITION af p-fraktil . Lad p være et vilkårligt tal mellem 0 og 1.
Ved p-fraktilen eller 100 p % fraktilen forstås det tal , for hvilket det gælder, at
F( x ) = P( X ≤ x ) = p ( ( ) )
p p
x p
= ∫ f x dx
0
x p
Særlig ofte benyttede fraktiler er 50% fraktilen, som kaldes medianen (eller 2. kvartil), 25 % fraktilen, som kaldes
nedre kvartil (eller 1. kvartil) og 75% fraktilen, som kaldes øvre kvartil (eller 3. kvartil).
Eksempel 3.4. Fordelingsfunktion for kontinuert variabel.
For den i eksempel 3.3 angivne kontinuerte variabel X med tæthedsfunktion f (x) ønskes fundet:
1) Fordelingsfunktionen F (x).
x
2) Medianen .
dx x
Løsning:
x
x
x x x
1) F( x) = f ( x) dx = + xdx=
x
.
x
+ dx=
⎡
⎧
⎪∫
0
−∞
⎪
⎪
⎤
∫
⎨0
⎢ ⎥ = ≤ ≤
−∞ ∫
0 2
⎪
⎣ 8 ⎦ 8
⎪
⎪0
+
⎩⎪
∫
2
= 0 for < 0
3
3
3 2
for
0
8
0
3
0 1 for x > 2
8 2
3
x
3
2) Medianen er bestemt ved F( x)
= 05 . ⇔ = 05 . ⇔ x = 4⇔ x = 159 . .
8
20

3.4 Linearkombination af stokastiske variable
3.4 LINEARKOMBINATION AF STOKASTISKE VARIABLE
Vi betragter i dette afsnit flere stokastiske variable.
Eksempel 3.5 vil blive benyttet som gennemgående eksempel
Eksempel 3.5. To variable.
Insektpulver sælges i papkartoner. Lad den stokastiske variable X 1 være vægten af pulveret, mens
X 2 er vægten af papkartonen. I middel fyldes der 500 gram insektpulver i hver karton med en
spredning på 5 gram. Kartonen vejer i middel 10 gram med en spredning på 1.0 gram.
Y = X 1 + X 2 er da bruttovægten.
1) Find middelværdien af Y
2) Find spredning af Y.
Mere generelt haves:
Lad X1, X2,..., Xnvære n stokastiske variable.
Ved en linearkombination af disse forstås
Y = a0 + a1 ⋅ X1 + a2 ⋅ X2 + ... + an ⋅ Xn
, hvor a0, a1, a2,..., aner konstanter.
Man kan vise (se eventuelt kapitel 9) at der gælder følgende
Linearitetsregel: E( Y) = a + a ⋅ E( X ) + a ⋅ E( X ) + ... + a ⋅E(
X ) .
0 1 1 2 2
21
n n
I eksempel 3.5 synes det rimeligt at antage, at vægten af pulveret og vægten af papkartonen er
uafhængige ( påfyldningen kan tænkes at ske maskinelt, uden at den er afhængig på nogen måde
af hvilken vægt, kartonen tilfældigvis har).
Man kan vise (se eventuelt kapitel 11, for en mere udførlig behandling af uafhængighed m.m.),
at hvis X1, X2,..., Xner statistisk uafhængige, gælder
Kvadratregel for statistisk uafhængige variable:
2
VY ( ) = a ⋅ V( X
2
) + a ⋅ V( X
2
) + ... + a ⋅V(
X )
1
1 2
2
n n
Eksempel 3.5. (fortsat) To variable.
Spørgsmål 1: E(Y) = E(X1) + E(X2) = 500 + 10 = 510 gram.
Spørgsmål 2: V(Y) = V(X1) + V(X2) = 5 2 + 1 2 = 26. σ ( Y ) = 26 = 51 . gram.
Ensfordelte uafhængige variable.
Lad os antage, at vi uafhængigt af hinanden og under de samme betingelser udtager n elementer
fra en population med middelværdi og spredning . Lad være den stokastiske variabel,
µ σ X 1
der er resultatet af første udtagning af et element i stikprøven, være den stokastiske variabel,
X 2
der er resultatet af anden udtagning, osv.
X1, X2,..., Xnvil da være ensfordelte uafhængige stokastiske variable, dvs. have samme
fordeling med middelværdi µ og spredning σ
.
.

3. Kontinuert stokastisk variabel
Eksempel 3.6. Ensfordelte variable
Bruttovægten af det i eksempel 3.4 nævnte karton insektpulver havde middelvægten 510 g med
en spredning på 5.1 g.
Vi udtager nu tilfældigt og uafhængigt af hinanden 10 pakker insektpulver.
a) Hvad bliver i middel den samlede vægt af de 10 kartonner
b) Hvad bliver i middel spredningen på den samlede vægt af de 10 kartoner
Løsning:
Lad X1 være vægten af karton 1, X2 være vægten af karton 2 osv. X10 være vægten af karton 10.
Y= X1 + X2 + ... + X10 er da vægten af alle 10 kartonner.
a) E(Y) = E(X1)+E(X2)+ . . . +E(X10) =10⋅ 510 = 5100 g
b) V(Y) = V(X1)+V(X2)+ . . . +V(X10) =10⋅ 26 = 260 g
σ ( Y ) = 260 = 1612 .
Bemærk: En almindelig fejl er her, at man tror, at Y=10 X og dermed V(Y)=102 ⋅ ⋅ V(X)=2600
Vi har her at gøre med 10 ensfordelte uafhængige variable, og ikke 10 ⋅ vægten af 1 karton.
For ensfordelte uafhængige stokastiske variable gælder:
SÆTNING 3.1 (middelværdi og spredning for stikprøves gennemsnit )
σ
X1 + X2 + ...
+ Xn
E( X)=
µ og σ ( X ) = , hvor X =
n
n
⎛ X + X + ... + X
Bevis: Af linearitetsreglen fås n
E( X) = E⎜
1 2
⎞ 1
⎟
⎜
⎟ ( ( ) ( ) ... ( ) )
n n E X E X E X = + + + = µ
⎝
⎠ 1 2 n
X + X + ... X 2 2
⎛ 1 1 n ⎞ 1
n ⋅ σ ο
Af kvadratreglen fås V( X) = V⎜
⎟ = ( V( X ) + V( X ) + ... + V( Xn) ) = = .
⎝ n ⎠ 2 1 2
2
n
n n
Eksempel 3.7. Spredning på gennemsnit (eksempel 3.5 fortsat)
Hvis der udtages 5 kartoner insektpulver, hvad vil da være spredningen på gennemsnittet af
vægten af insektpulveret .
Løsning:
Da spredningen på 1 karton er 5.1 gram, vil spredningen på gennemsnittet af 5 kartoner være
σ 51 .
σ ( X ) = = = 228 .
n 5
22

3.5 USIKKERHEDSBEREGNING
23
3.5 Usikkerhedsberegning
Ved enhver måling kan den fysiske størrelse aldrig måles eksakt. Målingen behæftes altid med
en vis usikkerhed. Det kan skyldes usikkerhed på objektet, måleinstrumentet, brugeren af
instrumentet osv.
Systematiske fejl er fejl, hvor man eksempelvis har glemt at korrigere for temperaturens indflydelse
på måling af et stofs hårhed.
Er målingen befriet for systematiske fejl, er der kun tilbage “tilfældige fejl”.
Eksempelvis vil der ofte på et instrument være anført en “instrumentusikkerhed”, som viser hvor
nøjagtigt instrumentet kan måle.
En sådan usikkerhed kan eksempelvis findes ved at man foretager en måling flere gange eventuelt
af forskellige personer.
Lad der eksempelvis være foretaget 5 målinger og resultaterne er x1, x2, x3, x4, x5
Lad gennemsnittet af de 5 målinger være x .
“Maksimal” usikkerhed
Den maksimale usikkerhed ∆x er så defineret som den numerisk største afvigelse mellem en målt
værdi og gennemsnittet.
Er eksempelvis en temperatur angivet som 30.45 0
± 0.05 menes hermed, at i værst tænkelige
tilfælde kunne målingen være 30.40 0 eller 30.50 0 .
Eksempel 3.8. Maksimal usikkerhed
Lad x = 153 ± 1m og y = 25 ± 2 m
Den maksimale usikkerhed på x - y er da 3m , dvs. x-y = 128 ± 3 m
Statistisk usikkerhed
Ved den statistiske usikkerhed regner man populært sagt med at fejlene til en vis grad ophæver
hinanden. Det er jo ret usandsynligt, hvis man har mange målinger, at de alle ligger i den samme
høje ende af usikkerhedsintervallet
Her siger man derfor at spredningen er et mål for usikkerheden.
Eksempel 3.9 Statistisk usikkerhed
Lad x = 153 med en spredning på 1m og y = 25 med en spredning på 2m
X og Y antages at være uafhængige målinger,
2 2
Den statistiske usikkerhed på x-y vil ifølge kvadratsætningen være σ = 1 + 2 = 5 = 224 . m
Relativ usikkerhed
∆x
Ved den relative usikkerhed på en størrelse x forstås størrelsen henholdsvis
x
1
I eksemplerne 3.7 og 3.8 er den relative usikkerhed på x således = 0. 65%
153
Usikkerheden på to størrelser kan jo godt være den samme , f.eks. 1 cm, men hvis den ene
størrelse er usikkerheden på diameteren af et rør på 10 cm og den anden er højden på en skyskraber,
så er det klart, at det er den relative usikkerhed, der siger mest.
s
x

3. Kontinuert stokastisk variabel
Eksempel 3.8 og 3.9 viser forskellen mellem de to definitioner af usikkerhed.
Vi vil i det følgende koncentrere os om den statistiske usikkerhed σ , som vi i det følgende kort
vil benævne usikkerheden.
Vi vil dog også kort angive, hvorledes tilsvarende beregninger af maksimal usikkerhed vil
forløbe.
Som eksemplerne 3.8 og 3.9 viser, er det let at udregne usikkerheden på summer og differenser
af to eller flere størrelser.
De følgende formler viser hvorledes man beregner usikkerheden på mere komplicerede udtryk.
Eksempel 3.10 Usikkerhed på sammensat udtryk
Måles trykket P, volumenet V og temperaturen T af en ideal gas , optræder der tilfældige
målefejl, som gør værdierne usikre. Beregnes molantallet n nu af ligningen
PV ⋅
PV ⋅ = n⋅RT ⋅ ⇔ n=
, bliver værdien af n derfor også usikker. Vi ønsker at kunne
RT ⋅
beregne usikkerheden på n ud fra usikkerhederne på P, V og T.
Sætning 3.2. (ophobningsloven for usikkerheder)
Lad X1,X2, . . . , X være uafhængige stokastiske variable, som hidrører fra målinger.
og lad X1 have usikkerheden σ 1 ,X2 have usikkerheden σ 2 osv.
Beregnes en ny størrelse Y = f ( X1, X2 ,..., Xn) , i et punkt P = ( x1, x2, ,..., xn) får Y en usikker-
hed σ ( Y)
som kan beregnes på følgende måde:
Lad ∂Y
∂Y
∂Y
( P) = a1,
( P) = a2,...,
( P) = an
∂X
∂X
∂X
1
Der gælder da
2
n
Ved den praktiske brug af formlerne for relative fejl og den ophobede fejl kan man erstatte alle
middelværdier med de faktisk målte værdier.
Bevis for ophobningsloven, Funktionen Y = f ( X1, X2,..., Xn) tilnærmes ved sit 1. Taylorpolynomium med
∂Y
∂Y
∂Y
udviklingspunkt i punktet P: Y = f ( X1, X2,..., Xn) ≈ Y( P)
+ ⋅( X1− x1)
+ ⋅( X2 − x2)
+ ... + ⋅( Xn −xn),
∂X1
∂X
2
∂X
n
hvor de partielle afledede er beregnet i punktet P. Vi finder derfor
∂Y
∂
∂
Y = f ( X1, X2,..., Xn) ≈ konstant + ⋅ + ⋅ + + ⋅
∂X
∂
∂
X
Y
Y
⎛
∂Y
∂Y
∂Y
⎞
1 X 2 ... X k , VY ( ) ≈ V⎜konstant
+ ⋅ X 1 + ⋅ X 2 + ... + ⋅ X k ⎟
1 X 2
X k
⎝ ∂X
1 ∂X
2
∂X
k ⎠
Da X1, X2,..., Xk er forudsat statistisk uafhængige, får vi ifølge kvadratreglen
Y
Y
Y
VY ( ) ≈ V( X ) V( X ) ... V( Xk)
X
X
X
⎛ ⎞
⎜ ⎟ ⋅ +
⎝ ⎠
⎛ ⎞
⎜ ⎟ ⋅ + +
⎝ ⎠
⎛
∂
∂
∂ ⎞
1
2 ⎜ ⎟ ⋅
∂
∂
⎝ ∂ ⎠
1
2
2
2
∂Y
∂Y
∂Y
σ ( Y)
≈ V( X ) V( X ) ... V( Xk)
∂X
∂X
∂X
⎛ ⎞
⎜ ⎟ ⋅ +
⎝ ⎠
⎛ ⎞
⎜ ⎟ ⋅ + +
⎝ ⎠
⎛ ⎞
1
2 ⎜ ⎟ ⋅
⎝ ⎠
1
2
2
2
σ( Y) ≈ a1⋅ σ1+ a2⋅ σ2+ ... + an ⋅σn
2
2
2
2 2 2
For den maksimale usikkerhed gælder med de samme betegnelser som ved ophobningsloven:
∆Y = a1 ∆x1 + a2 ∆x2 + ... + an ∆xn
(svarer til differentialet for en funktion)
k
k
2
2
24

25
3.5 Usikkerhedsberegning
Eksempel 3.11. Usikkerhedsberegning.(fortsættelse af eksempel 3.10)
PV ⋅
−1 −1
En ideal gas opfylder ligningen n = , hvor R = 8314 . J⋅K⋅mol .
RT ⋅
Man har målt P = 123400 Pa , V = 567 . m ,
3
T = 678 K
med usikkerheder σ ( P ) = 1000 Pa , σ ( V ) = 006 . m og .
3 σ ( T ) = 3K
Det kan antages, at måleresultaterne for P, V og T er statistisk uafhængige.
a) Find molantallet n, usikkerheden σ ( n) , samt den relative usikkerhed rel( n)
.
Man skønner, at der for de maksimale absolutte fejl gælder
P = 123400 3000 Pa V = 5.67 0.18 m3 ± ± og T = 678 ± 9 K
b) Find den maksimale usikkerhed på n , og den relative maksimale usikkerhed på n.
Løsning
Håndregning:
n mol
PV ⋅ 123400 ⋅ 5. 67
= =
= 12412 .
R ⋅ T 8314 . ⋅ 678
Af ophobningsloven for usikkerheder fås usikkerheden på n:
∂n
V
=
∂P
RT ⋅ =
567 .
∂n
P
= 0. 001006
=
8. 314⋅ 678
∂V
RT ⋅ =
123400
= 218915 .
8. 314⋅ 678
∂n
PV
=
∂T
RT
− ⋅
=
⋅
− ⋅ 123400 567 .
= 0183075 .
2 2
8. 314 ⋅678
a) σ
2
∂n
∂n
∂n
( n)
= σ ( P)
σ ( V ) σ ( T)
∂P
∂V
∂T
⎛ ⎞
⎜ ⎟ ⋅ +
⎝ ⎠
⎛ ⎞
⎜ ⎟ ⋅ +
⎝ ⎠
⎛
2
2 ⎞ 2
⎜ ⎟ ⋅
⎝ ⎠
2
= 0. 001006 ⋅ 1000 + 218915 . ⋅ 0. 06 + 0183075 . ⋅3
2 2 2 2 2 2
= 101178 . + 172526 . + 0. 30165 = 174318 . = 174 . mol
2
σ ( n)
174318 .
og dermed den relative usikkerhed rel( n)
= = = 0. 0140443 ≈140%
. .
n 124. 12
n
b) d n = dn
mol
P dP
n
V dV
n
T dT
∂ ∂ ∂
= + + = 0. 00106⋅ 3000 + 218915 . ⋅ 018 . + 0183075 . ⋅ 9 = 8. 768
∂ ∂ ∂
dn ( ) 18. 768
rel( n)
= = = 706% .
n 12412 .
TI 89
p*v/(8.314*t) STO n
n v=5.67 and p=123400 and t=678 Resultat n = 124.12
d(n,p) v=5.67 and p=123400 and t=678 STO a
d(n,v) v=5.67 and p=123400 and t=678 STO b
d(n,t) v=5.67 and p=123400 and t=678 STO c
a) ((a*1000)^2+(b*0.06)^2+(c*3)^2) Resultat σ( n ) = 17432 .
rel(n) =1.7432/124.12 = 0.0140 = 1.4%
b) a*3000+b*0.18+c*9 = rel(n)=8.768//12412 )= 0.0706
Excel Ikke muligt, da ikke kan differentiere.
,

Statistiske grundbegreber
OPGAVER
Opgave 3.1
Givet følgende funktion:
1
⎧ 4 ( 3− x) for 0< x<
2
f ( x)
= ⎨
⎩0
ellers
∫
1) Vis, at f (x) opfylder betingelsen f ( x) dx = 1 der indgår i kravet til en tæthedsfunktion.
a
b
Idet følgende antages, at f ( x ) er tæthedsfunktion for en stokastisk variabel X .
2) Skitser grafen for f (x ) , find den tilsvarende fordelingsfunktion F ( x ) og skitser også dennes graf.
3) Beregn middelværdien E(X), variansen V (X ) og spredningen σ ( X ) .
4) Bestem P(. 025≤ X < 05 .)
Opgave 3.2
Givet følgende funktion:
⎧ 3
⎪ for 1≤ x
4
f ( x) = ⎨ x
⎪
⎩0
ellers
b
1) Vis, at f (x) opfylder betingelsen f ( x) dx = 1 der indgår i kravet til en tæthedsfunktion.
∫
a
Idet følgende antages, at f ( x ) er tæthedsfunktion for en stokastisk variabel X .
2) Skitser grafen for f (x ) , find den tilsvarende fordelingsfunktion F ( x ) og skitser dens graf.
3) Beregn middelværdien E(X), variansen V (X ) og spredningen σ ( X ) .
4) Bestem P( 2≤ X ≤3)
.
Opgave 3.3
Vægten af en (tilfældigt udvalgt) tablet af en vis type imod hovedpine har middelværdien
µ = 065 . g og spredningen σ = 004 . g
Beregn middelværdi og spredning af den sammenlagte vægt af 100 (tilfældigt udvalgte) tabletter
Opgave 3.4
En mængde råmateriale til en produktion ligger i kegleformet bunke. En kegle med radius R og
højde H har volumenet V = R H .
π 2
3
Man har målt R = 12. 0 m , H = 110 . m ,
med usikkerheder σ ( R ) = 02 . m , σ ( H ) = 01 . m .
Det kan antages, at måleresultaterne for R og H er statistisk uafhængige.
Find volumenet V, usikkerheden σ ( V ) , samt den relative usikkerhed rel( V ).
Opgave 3.5
For en rektangulær flade har man målt længden L og bredden B :
L = 12. 3 m , B = 84 . m
med usikkerheder
σ ( L ) = 01 . m , σ ( B ) = 02 . m .
Det kan antages, at måleresultaterne for L og B er statistisk uafhængige.
Find fladens areal A, usikkerheden σ ( A) , samt den relative usikkerhed rel( A)
.
26

27
Opgaver til kapitel 3
Opgave 3.6
For et bassin af form som en retvinklet kasse har man målt længden L , bredden B og højden H
:
L = 18. 0 m , B = 12. 3 m H = 45 . m
med usikkerheder σ ( L ) = 02 . m , σ ( B ) = 01 . m , σ ( H ) = 02 . m.
Det kan antages, at måleresultaterne for L, B og H er statistisk uafhængige.
Find bassinets volumen V, usikkerheden σ ( V ) , samt den relative usikkerhed rel( V ).
Opgave 3.7
På den viste forsøgsopstilling kan man foretage målinger til bestemmelse af et stofs længdeudviddelseskoefficient.
l1 er længden af stangen ved starttemeraturen t1. l2 er længden af stangen ved sluttemeraturen t2. Under forsøget er følgende størrelser bestemt.
l1 = 500 ± 0.1 mm
l2 = 500.48 ± 0.1 mm
t2 - t1 = 78 0 0.1 0 ± C
l2 − l1
Længdeudvidelseseskoefficienten k kan bestemmes af udtrykket k =
l2( t2 − t1)
a) Find den maksimale usikkerhed på k
b) Find den relative maksimale usikkerhed på k.
Idet man nu antager, at man har den erfaring, at spredningen på størrelserne er 0.1, skal man
c) Finde den statistiske usikkerhed på k
d) Find den relative statistiske usikkerhed på k.

4.Normalfordelingen.
4 NORMALFORDELINGEN
4.1 INDLEDNING
Lad os som eksempel tænke os et kemisk forsøg, hvor vi måler udbyttet af et stof A. Selv om vi
gentager forsøget ved anvendelse af den samme metode og i øvrigt søger at gøre forsøgsbetingelserne
så ensartet som muligt, varierer udbyttet dog fra forsøg til forsøg. Disse variationer fra den
ene forsøg til det næste må skyldes forhold vi ikke kan styre. Det kan skyldes små ændringer i
temperaturen, i luftens relative fugtighed, vibrationer under fremstillingen, små forskelle i de
anvendte råmaterialer (kornstørrelse, renhed), forskelle i menneskelig reaktionsevne osv. Hvis
ingen af disse variationsårsager er dominerende, der er et stort antal af dem, de er uafhængige og
lige så godt kan have en positiv som en negativ indvirkning på resultatet, så vil den totale fejl
sædvanligvis approksimativt være fordelt efter den såkaldte normalfordeling. (også kaldet
Gauss-fordelingen)
Som illustration af dette kan anvendes Galtons apparat.
Eksempel 4.1. Eksperiment med et Galton-apparat.
På den anførte figur er skitseret et Galton-apparat.
A er en tragt; B er sømrækker, hvor sømmene i en
underliggende række er anbragt midt ud for mellemrummene
mellem sømmene i den overliggende række;
C er opsamlingskanaler.
Lader man mange kugler passere gennem tragten A
ned gennem sømrækkerne B til opsamlingskanalerne
C, vil man konstatere, at de enkelte kugler nok bliver
tilfældigt fordelt i opsamlingskanalerne, men at kuglernes
samlede fordeling giver et mønster, som gentages,
hver gang man udfører eksperimentet. Fordelingen er hver gang med tilnærmelse en
klokkeformet symmetrisk fordeling som skitseret på tegningen, noget som er karakteristisk
for normalfordelingen.
Galton-apparatet illustrerer, hvorfor man så ofte antager, at måleresultater er værdier af en
normalfordelt variabel: Hver sømrække repræsenterer en faktor, hvis niveau det ikke er muligt
at holde konstant fra måling til måling, og sømrækkernes påvirkning af kuglens bane symboliserer
den samlede virkning, som de ukontrollerede faktorer har på størrelsen af den målte
egenskab.
28

4.2 Definition og sætning om normalfordeling
En anden illustration af under hvilke omstændigheder en normalfordelt variabel kan forekomme
i praksis så vi i kapitel 2 eksempel 2.5 hvor man på 75 mennesker med en bestemt ledsygdom
målte pH i knæleddet.
Histogrammet som er gentaget nedenfor har et klokkeformet udseende, som kraftigt antyder, at
den kontinuerte stokastiske variabel X = pH er normalfordelt.
I den teoretiske statistik giver den centrale grænseværdisætning en forklaring på, hvorfor
normalfordelingen er en god model ved mange anvendelser.
Den centrale grænseværdi 1 siger (løst sagt), at selvom man ikke kender fordelingen for de n
ensfordelte stikprøvevariable X1, X2,..., Xn, så vil gennemsnittet X være approksimativt
normalfordelt blot n er tilstrækkelig stor (i praksis over 30) . 2
4.2 DEFINITION OG SÆTNINGER OM NORMALFORDELING
Definition af normalfordeling n( µ , σ )
Nornalfordelingen er sandsynlighedsfordelingen for en kontinuert stokastisk variabel X med
tæthedsfunktionen f(x) bestemt ved f ( x)= Den har middelværdi µ og spredning σ
2
1 ⎛ x−
µ ⎞
− ⋅ 1
⎜ ⎟
2 ⎝ σ ⎠
⋅ e
2 ⋅π ⋅σ
for ethvert x
Grafen er klokkeformet og symmetrisk om linien x = µ .
1
Den centrale grænseværdi sætning. Lad som ovenfor X være gennemsnittet for en stikprøve af størrelsen n taget fra
en population med middelværdi µ og spredning σ .
StørrelsenU vil da for n gående mod være normeret normalfordelt.
X − µ
=
∞
σ
n
2 ⎛ ( X − µ ) n⎞
P⎜ ⎟ →φ( u) for n→
∞
⎝ σ ⎠
20
18
16
14
12
10
8
6
4
2
0
Hyppighed
6,94 7,02 7,1 7,18 7,26 7,34 7,42 7,5 7,58 7,66 Mere
At f (x ) virkelig er en tæthedsfunktion med de angivne egenskaber vises i “Supplement til
statistiske grundbegreber afsnit 2.A”
29
Hyppighed

4.Normalfordelingen.
For at få et overblik over betydningen af µ og σ er der nedenfor afbildet tæthedsfunktionen for
normalfordelingerne n(0 , 1), n(4.8 , 2.2), n(4.8 , 0.7) og n(10 , 1).
0,6
0,5
0,4
0,3
0,2
0,1
0
-7 -3 1 5 9 13 17
Fig 4.1 Forskellige normalfordelinger
30
0,1
4,8,2,2
4,8,0,7
10,1
Det ses, at tæthedsfunktionerne er klokkeformede, og at et interval på [ µ −3⋅ σ ; µ + 3⋅σ]
indeholder stort set hele sandsynlighedsmassen.
Vi nævner uden bevis følgende sætning:
SÆTNING 4.1 (Additionssætning for linearkombination af normalfordelte variable).
Er Y en linearkombination af n stokastisk uafhængige , normalfordelte variable, vil Y også
være normalfordelt.
Kendes middelværdi og spredning for de n normalfordelte variable , kan man ved anvendelse af
linearitetsregel og kvadratregel finde Y’s middelværdi og spredning.
Endvidere følger det af additionssætningen, og sætning 3.1, at gennemsnittet x er normalfordelt
σ
med en spredning på .
n

3
Normeret normalfordeling
Af særlig interesse er den såkaldte normerede normalfordeling.
Den er bestemt ved at have middelværdien 0 og spredningen 1.
Grafen for den er tegnet i figur 4.1
1
ϕ(
u) = e
2⋅
π
2
u
−
2
for ethvert u
4 1 u −
Φ ( u) = ⋅ e 2 dt
2 ⋅ π ∫∞
t
2
4.2 Definition og sætning om normalfordeling
Den kaldes sædvanligvis U eller Z og dens fordeling U- eller Z-fordelingen . Dens tæthedsfunktion
3 benævnes og dens fordelingsfunktion 4 .
ϕ Φ
Specielt vil dens p - fraktil u p indgå i adskillige formler i de næste afsnit.
Den kan naturligvis beregnes ved anvendelse af eksempelvis TI89 eller Excel, (se afsnit 4.3) men
da de så ofte indgår i beregningerne er der i tabel 1 angivet værdier af den for specielt ofte
forekommende p -værdier.
En vigtig sammenhæng mellem fraktiler for X og fraktiler for U er følgende
xp = up
⋅ σ + µ
31
(4.1)
Beviset for denne relation indgår i beviset for den følgende sætning, som også viser, at man kan
overføre en vilkårlig normalfordeling til den normerede normalfordeling.
Det er derfor nok at lave en tabel over den normerede normalfordeling.
Dette er det man udnytter, hvis man ikke har rådighed over et program, der som beskrevet i afsnit
4.3 direkte kan beregne værdierne.
Der gælder følgende

4.Normalfordelingen.
SÆTNING 4.2. (normering af normalfordeling). Når X er normalfordelt
er den variable U normalfordelt , og der gælder
X − µ
=
n( 01 ,)
σ
⎛ b − µ ⎞
P( X ≤ b)
= Φ⎜
⎟
⎝ σ ⎠
og
⎛ b−µ ⎞ ⎛ a−µ
⎞
Pa ( < X≤ b)
= Φ⎜⎟−Φ⎜⎟. ⎝ σ ⎠ ⎝ σ ⎠
Endvidere gælder xp = up
⋅ σ + µ
Bemærk, at det for de to formler er ligegyldigt, om ulighederne er med eller uden lighedstegn.
Bevis:
At U også er normalfordelt vises ikke her.
∞
∞
∞
⎛ X − µ ⎞ x − µ 1 µ
1 µ
EU ( ) = E⎜ ⎟ = f( xdx ) = x⋅ f( xdx ) − f( xdx ) = E( X)
− = 0
⎝ σ ⎠ ∫−∞
σ σ∫−∞
σ∫−∞ σ σ
∞ 2
∞
⎛ X − µ ⎞ ⎛ x − µ ⎞
1
2 V( X)
VU ( ) = V⎜ ⎟ = ⎜ ⎟ f ( x) dx = ( x − µ ) ⋅ f ( x) dx = = 1
⎝ σ ⎠ ∫−∞⎝
σ ⎠
2
σ ∫
2
−∞
σ
U har derfor middelværdi 0 og spredning 1.
X − b
b b
Endvidere fås P( X ≤ b) = P ≤ PU og
−
⎛
⎞
⎜
⎟ = ≤
⎝
⎠
− ⎛
µ µ
µ ⎞ ⎛ − µ ⎞
⎜ ⎟ = Φ⎜
⎟
σ σ ⎝ σ ⎠ ⎝ σ ⎠
Pa X b P a ⎛ − µ b−µ ⎞ ⎛ b−µ ⎞ ⎛ a−µ
⎞
( < ≤ ) = ⎜ < U≤ ⎟ = Φ⎜⎟−Φ⎜⎟ ⎝ σ σ ⎠ ⎝ σ ⎠ ⎝ σ ⎠
⎛ x p − ⎞ x p
Bevis for formel 2.1: P( X ≤ xp) = p⇔
⎜ ⎟ = p ⇔ up xp up
⎝ ⎠
−
µ
µ
Φ
= ⇔ = ⋅ σ + µ
σ
σ
4.3. BEREGNING AF SANDSYNLIGHEDER
Stikprøves gennemsnit og spredning.
Ofte er middelværdien µ og spredningen σ ukendt i en foreliggende normalfordeling. I så fald
erstattes fordelingen n( µ , σ ) i praksis med en approksimerende fordeling nxs ( , ) , såfremt der
foreligger et rimelig stort antal observationer fra den givne fordeling.
På basis af den i eksempel 1.5 angivne stikprøve på 75 patienter beregnes et gennemsnit af pH
værdierne på 546. 52
SAK
x = = 7. 2868 og en s værdi på s =
.
75
n − = 0134355 .
1
Vi vil altså antage, at pH værdierne er approksimativt normalfordelt n (7.29, 0.134).
32
n( µ , σ )

Ønsker vi at benytte ovenstående normal
fordeling n (7.29, 0.134) til at finde sandsynligheden
for, at pH er mindre end 7.2, er
denne sandsynlighed lig med arealet af det
skraverede areal under tæthedsfunktionen.
Ønsker vi tilsvarende at beregne sandsynligheden
for, at pH ligger mellem 7.2 og 7.5 er sandsynligheden
lig med det skraverede areal
under kurven på omstående figur.
Eksempel 4.1. Beregning med TI89 og Excel
Lad X være normalfordelt n( µ , σ ) , hvor µ = 7.29 og σ = 0.134.
1) Find P( X ≤ 72 . )
2) Find P(. 72≤ X ≤75
.)
3) Find P( X ≥ 76 . )
4) Find 90% fraktilen
Løsning:
x09 .
33
4.3. Beregn af sandsynligheder
TI89: Man finder de benyttede sandsynlighedsfordelinger ved at trykke på CATALOG F3
1) normCdf( , 7.2, 7.29, 0.134) = 0.2509
P( X ≤ 72 . ) = −∞
2) P(. 72≤ X ≤75
.) = normCdf( 7.2,7,5, 7.29, 0.134) = 0.691
3) P( X ≤ 76 . ) = normCdf( 7.6, ∞ 7.29, 0.134) = 0.2509
4) Har man omvendt givet en sandsynlighed p = 0.9 og ønsker at finde den tilsvarende
værdi x p for hvilken P( X ≤ xp) = 09 . betyder det, at man kender arealet 0.9 og skal
finde x-værdien.
Det svarer jo til at finde den inverse (omvendte) funktion af normalfordelingen.
x09 . = invnorm(0.6, 7.29, 0.134) = 7.462
Excel: Man finder de benyttede sandsynlighedsfordelinger ved på værktøjslinien foroven:
Tryk f x Vælg kategorien “Statistisk”
1) P( X ≤ 72 . ) = NORMFORDELING(7,2;7,29;0,134,1)=0.2509.
2) Beregningen sker i Excel ved (se det skraverede areal på figuren ) at beregne arealet fra −∞til
7.5 og
derfra trække arealet fra til 7.2, dvs.
−∞
P( 72 . ≤ X ≤ 75 .) = P( X ≤72 .) − P( X ≤ 75 .) =
NORMFORDELING(7,5;7,29;0,134;1)-NORMFORDELING(7,2;7,29;0,134;1)=0,691

4.Normalfordelingen.
3) Da arealet under kurven er 1, fås
P( X ≥ 76 . ) = 1− P( X < 76 . )
4) x09 . = NORMINV(0.9, 7.29, 0.134) = 7.462 .
=1-NORMFORDELING(7,6;7,29;0,134;1)= 0,01035
Eksempel 4.2. Kvalitetskontrol.
En fabrik støber plastikkasser. Fabrikken får en ordre på kasser, som blandt andet har den
specifikation, at kasserne skal have en længde på 90 cm. Kasser, hvis længder ikke ligger mellem
tolerancegrænserne 89.2 og 90.8 cm bliver kasseret.
Det vides, at fabrikken producerer kasserne med en længde X, som er normalfordelt med en
spredning på 0.5 cm.
a) Hvis X har en middelværdi på 89.6, hvad er så sandsynligheden for, at en kasse har en længde,
der ligger indenfor tolerancegrænserne.
b) Hvor stor er sandsynligheden for at en kasse bliver kasseret, hvis man justerer støbningen, så
middelværdien bliver den der giver den mindste procentdel kasserede (spredningen kan man
ikke ændre).
Fabrikanten finder, at selv efter den i spørgsmål 2 foretagne justering kasseres for stor en
procentdel af kasserne. Der ønskes højst 5% af kasserne kasseret.
c) Hvad skal spredningen σ formindskes til, for at dette er opfyldt?
Hvis det er umuligt at ændre σ , kan man prøve at få ændret tolerancegrænserne.
d) Find de nye tolerancegrænser (placeret symmetrisk omkring middelværdien 90,0) idet spredningen
stadig er 0.5, og højst 5% må kasseres.
En ny maskine indkøbes, og som et led i en undersøgelse af, om der dermed er sket ændringer
i middelværdi og spredning produceres 12 kasser ved anvendelse af denne maskine.
Man fandt følgende længder: 89.2 90.2 89.4 90.0 90.3 89.7 89.6 89.9 90.5 90.3 89.9 90.6.
e) Angiv på dette grundlag et estimat for middelværdi og spredning.
LØSNING:
TI89: Man finder de benyttede sandsynlighedsfordelinger ved at trykke på CATALOG F3
a) P( 89. 2 ≤ X ≤ 908 . ) = normCdf(89.2, 90.8, 89.6, 0.5)= 0.7799 = 77.99%
b) Middelværdien justeres til midtpunktet 90.0
P( X > 908 . ) + P( X < 89. 2) = normCdf(90.8 , ∞ , 90, 0.5)+normCdf(- ∞ ,89.2, 90, 0.5)= 10.96%
c) Da der ligger 5% udenfor intervallet, så må af symmetrigrunde 2,5% ligge på hver sin side
af intervallet. Vi har følgelig, at vi skal finde spredningenσ så P( X ≤ 89. 2) = 0. 025
08 .
Metode 1:Af relationen (4.1) fås 89. 2 = 0025 . ⋅ + 90 ⇔ = .
−
u σ σ
u
34
0025 .
Da =−196 . ( findes af tabel 2 eller ved invNorm(0.025,0,1)) fås σ = 0. 408
u0. 025
Metode 2: solve( normCdf( −∞ ,89.2, 90,x)=0.025,x) x > 0
eller solve(invNorm(0.025,90,x)=89.2,x) x > 0 Resultat x = σ = 0. 408
d) Kaldes den nedre tolerancegrænse for a fås med samme begrundelse som i punkt c :
P( X ≤ a)
= 0. 025.
Vi kan her benytte den “inverse” normalfordeling

Nedre grænse a = invNorm(0.025, 90,0.05) = 89.02
Øvre grænse b = 90 +(90 - 89.02) = 90.98
e) APPS Stat/List indtastning af de 12 tal i list1 F4 :Calc Udfylde menu
Man finder x = 89. 97 og s = 0435 .
Excel: Man finder de benyttede sandsynlighedsfordelinger ved
På værktøjslinien foroven: Tryk f x Vælg kategorien “Statistisk”
a) P( 89. 2 ≤ X ≤ 908 . ) = P( X ≤908 . ) − P( X ≤ 89. 2)
=
NORMFORDELING(90,8;89,6;0,5;1) - NORMFORDELING(89,2;89,6;0,5;1)=0,7799
b) Middelværdien justeres til midtpunktet 90.0
P( X > 908 . ) + P( X < 89. 2) = 1−P( X ≤ 908 . ) + P( X < 892 . ) =
1 -NORMFORDELING(90,8;90;0,5;1) - NORMFORDELING(89,2;90;0,5;1) = 0.1096
35
4.3. Beregn af sandsynligheder
89. 2 − 90
c) Metode 1:Ved indsættelse i ligningen xp = up
⋅ σ + µ fås 89. 2 = u0025
. ⋅ σ + 90 ⇔ σ =
u0025
.
σ =(89,2-90)/NORMINV(0,025;0;1)=0,408171 ≈ 0.408
Metode 2: I celle A1 skrives en startværdi for σ eksempelvis 0,5.
I celle B1 skrives =NORMFORDELING(89,2;90;A1;1)
2003: Funktioner “Målsøgning”
2007: Data Hvad-hvis analyse ”Målsøgning
I “Angiv celle” skrives B1. I “Til Værdi” skrives 0,025. I “Ved ændring af celle” skrives A1.
Facit :0,408444
d) Med samme begrundelse som under punkt c fås:
P( 90. 0 − d < X < 90. 0 + d) = 0. 95 ⇔ P( X ≤ 90. 0 − d) = 0. 025 og P( X ≤ 90. 0 + d)
= 0. 975 .
Vi får nedre grænse =NORMINV(0,025;90;0,5) = 89,02002 = 89.0
Øvre grænse =NORMINV(0,975;90;0,5) = 90,97998 = 91.0
5) Ved indtastning af de 12 tal i Excel i cellerne A1 til A12 findes
x = Middel( A1: A12)
= 8997 . og s = STDAFV(A1:A2) = 0.435
Eksempel 4.3. Additionssætning.
En boreproces fremstiller huller med en diameter X 1 , der er normalfordelt med en middelværdi µ 1
og en spredning på 0.04. En anden proces fremstiller aksler med en diameter X 2 , der er
normalfordelt med en middelværdi µ 2 og en spredning på 0.03.
Antag, at µ 1 = 10. 00 , og at µ 2 = 994 . .
Find sandsynligheden for, at en tilfældig valgt aksel har en mindre diameter end en tilfældig valgt
borehul.
LØSNING:
P( X2 < X1) = P( X2 − X1
< 0).
Sættes Y = X − X er Y normalfordelt.
2 1
EY ( ) = E( X2) − E( X1)
= 994 . − 1000 . = −006
.
2
2
2 2
V( Y) = 1 V( X ) + ( − 1) V( X ) = 0. 04 + 0. 03 = 0. 025
.
σ ( Y ) = 0. 0025 = 0. 05
2
1
TI89: PX ( 2 < X1) = PY ( < 0)
= normCdf( − ∞ , 0, -0.06, 0.05) = 0.8849 = 88.49%
Excel: P( X2 < X1) = P( Y < 0)
=
NORMFORDELING(0;-0,06;0,05;1) = 0.8849

4.Normalfordelingen.
OPGAVER
Opgave 4.1
1) En stokastisk variabel X er normalfordelt med µ = 0 og σ = 1.
Find P( X ≤ 075 . ), P( X > 16 . ) og P(. 075< X < 16 .).
2) En stokastisk variabel X er normalfordelt med µ = 25.1 og σ = 2.4.
Find P( 22. 3 < X ≤ 27. 8)
.
Opgave 4.2
Maksimumstemperaturen, der opnås ved en bestemt opvarmningsproces, har en variation der er
tilfældig og kan beskrives ved en normalfordeling med en middelværdi på 113.3 o og en spredning
på 5.6 o C.
1) Find procenten af maksimumstemperaturer, der er mindre end 116.1 o C.
2) Find procenten af maksimumstemperaturer, der ligger mellem 115 o C og 116.7 o C.
3) Find den værdi, som overskrides af 57.8% af maksimumstemperaturerne.
Man overvejer at gå over til en anden opvarmningsproces. Man udfører derfor 16 gange i løbet
af en periode forsøg, hvor man måler maksimumstemperaturen, der opnås ved denne nye proces.
Resultaterne var
116.6 , 116,6 , 117,0 , 124,5 , 122,2 , 128,6 , 109,9 , 114,8 , 106,4 , 110,7, 110,7 , 113,7 , 128,1,
118,8 , 115,4 , 123,1
4) Giv et estimat for middelværdien og spredningen.
Opgave 4.3
En fabrik planlægger at starte en produktion af rør, hvis diametre skal opfylde specifikationerne
2,500 cm ± 0,015 cm.
Ud fra erfaringer med tilsvarende produktioner vides, at de producerede rør vil have diametre,
der er normalfordelte med en middelværdi på 2,500 cm og en spredning på 0,010 cm. Man ønsker
i forbindelse med planlægningen svar på følgende spørgsmål:
1) Hvor stor en del af produktionen holder sig indenfor specifikationsgrænserne.
2) Hvor meget skal spredningen σ ned på, for, at 95% af produktionen holder sig indenfor
specifikationsgrænserne (middelværdien er uændret på 2,500 cm).
3) Fabrikken overvejer, om det er muligt at få indført nogle specifikationsgrænser (symmetrisk
omkring 2,500), som bevirker, at 95% af dets produktion falder indenfor grænserne. Find disse
grænser, idet det stadig antages at middelværdien er 2.500 og spredningen 0.010 cm.
Opgave 4.4
En automatisk dåsepåfyldningsmaskine fylder hønskødssuppe i dåser. Rumfanget er normalfordelt
med en middelværdi på 800 ml og en spredning på 6,4 ml.
1) Hvad er sandsynligheden for, at en dåse indeholder mindre end 790 ml?.
2) Hvis alle dåser, som indeholder mindre end 790 ml og mere end 805 ml bliver kasseret, hvor
stor en procentdel af dåserne bliver så kasseret?
3) Bestem de specifikationsgrænser der ligger symmetrisk omkring middelværdien på 800 ml,
og som indeholde 99% af alle dåser.
36

37
Opgaver til kapitel 4
Opgave 4.5
I et laboratorium lægges et nyt gulv.
Det forudsættes, at vægten Y der hviler på gulvet, er summen af vægten X1 af maskiner og
apparater og vægten X2 af varer og personale, dvs. Y = X1 + X2 Da både X1 og X2 er sum af mange relativt små vægte, antages det, at de er normalfordelte.
Det antages endvidere at X1 og X2 er statistisk uafhængige.
Erfaringer fra tidligere gør det rimeligt at antage, at der gælder følgende middelværdier og
spredninger (målt i tons):
E(X1) = 6.0, σ ( X 1) = 1.2, E(X2) = 3.5, σ ( ) = 0.4.
1) Beregn E(Y) og σ ( Y)
.
X 2
2) Beregn det tal y 0 , som vægten Y med de ovennævnte forudsætninger kun har en sandsynlighed
på 1% for at overskride.
3) Beregn sandsynligheden for, at vægten af varer og personale en tilfældig dag, efter at det nye
gulv er lagt, er større end vægten af maskiner og apparater. (Vink: se på differensen X 2 - X 1)
Opgave 4.6
Ved fabrikation af et bestemt mærke opvaskemiddel fyldes vaskepulver i papkartoner.
I middel fyldes 4020 g pulver i hver karton, idet der herved er en spredning på 12 g.
Pulverfyldningen kan forudsættes ikke at afhænge af kartonernes vægt, der i middel er 250 g med
en spredning på 5g.
Beregn sandsynligheden p for, at en tilfældig pakke opvaskemiddel har en bruttovægt mellem
4250 g og 4300 g.
Opgave 4.7
Et system er af sikkerhedsmæssige grunde opbygget af to apparater A, der er parallelforbundne
(se figur) således, at systemet virker, så længe blot et af apparaterne
virker.
Svigter et af apparaterne, startes reparation. Det antages, at
reparationstiden er normalfordelt med middelværdien
µ rep = 10 timer og spredning σ rep = 3 timer.
I reparationstiden overbelastes den anden komponent, og det
antages, at dens levetid fra reparationens start (approksimativt) er normalfordelt med middelværdi
µ og spredning σ = 4 timer.
1) Find sandsynligheden for, at reparationen er afsluttet, inden den anden komponent fejler, hvis
µ = 20 timer.
2) Hvor stor skal µ være, for at sandsynligheden for, at reparationen kan afsluttes før den anden
komponent fejler, er mere end 99.9%?
Opgave 4.8
Vægten af en (tilfældig udvalgt) tablet af en vis type mod hovedpine har middelværdien 0.65 g
og spredningen 0.04 g.
1) Beregn middelværdi og spredning af den sammenlagte vægt af 100 (tilfældigt udvalgte )
tabletter.
2) Antag, at man benytter følgende metode til at fylde tabletter i et glas. Man placerer glasset på
en vægt og fylder tabletter på, indtil vægten af tabletterne i glasset overstiger 65,3 g. Beregn
sandsynligheden for, at glasset kommer til at indeholde mere end 100 tabletter (se bort fra
vægtens fejlvisning).

5 Stikprøver
5. STIKPRØVER
5.1 UDTAGNING AF STIKPRØVER
I langt de fleste i praksis forekomne tilfælde vil det bl.a. af tidsmæssige og omkostningsmæssige
grunde være umuligt at foretage en totaltælling af hele populationen. Helt klart er dette ved
afprøvningen ødelægger emnet (åbning af konservesdåser) eller populationen i princippet er
uendelig ( for at undersøge om en metode giver et større udbytte end et andet, udføres en række
kemiske forsøg og her er der teoretisk ingen øvre grænse for antal delforsøg)
Som det senere vil fremgå kan selv en forholdsvis lille repræsentativ stikprøve give svar på
væsentlige forhold omkring hele populationen.
Det er imidlertid klart, at en betingelse herfor er, at stikprøven er repræsentativ, dvs. at
stikprøven med hensyn til den egenskab der ønskes er et “mini-billede” af populationen.
For at opnå det, foretager man en eller anden form for lodtrækning (kaldes randomisering).
Afhængig af problemet kan dette gøres på forskellig måde.
Simpel udvælgelse: Den enkleste form for stikprøveudtagning er, at man nummererer
populationens elementer, og så randomiserer (ved lodtrækning, evt. ved at benyttet et program
der generer tilfældige tal) udtager de N elementer der skal indgå i stikprøven.
Eksempel: For at undersøge om en ændring af vitaminindholdet i foderet for svin ændrede deres
vægt, udvalgte man ved randomisering de svin, som fik det nye foder.
Stratificeret udvælgelse.
Under visse omstændigheder er det fordelagtigt (mindre stikprøvestørrelse for at opnå samme
sikkerhed) at opdele populationen i mindre grupper (kaldet strada), og så foretage en simpel
udvælgelse indenfor hver gruppe. Dette er dog kun en fordel, hvis elementerne indenfor hver
gruppe er mere ensartet end mellem grupperne.
Eksempel: Ønsker man at spørge vælgerne om deres holdning til et politisk spørgsmål (f.eks. om
deres holdning til et skattestop) kunne det måske være en fordel at dele dem op i indkomstgrupper
(høj, mellem og lav) .
Systematisk udvælgelse:
Ved en såkaldt systematisk udvælgelse, vælger man at udtage hver k’te element fra populationen.
Eksempel: En detailhandler ønsker at måle tilfredsheden hos sine kunder. Der ønskes udtaget 40
kunder i løbet af en speciel dag.
Da man naturligvis ikke på forhånd kender de kunder der kommer i butikken, vælges en
systematisk udvælgelse, ved at vælge hver 7'ende kunde der forlader butikken. Man starter dagen
med ved lodtrækning at vælge et af tallene fra 1 til 7. Lad det være tallet 5. Man udtager nu kunde
nr. 5, 5+ 1⋅ 7 = 12, 5+ 2⋅ 7 = 19,..., 5+ 39⋅ 7 = 278 . Derved har man fået valgt i alt 40 kunder.
Problemet er naturligvis, om tallet 7 er det rigtige tal. Hvis man får valgt tallet for stort,
eksempelvis sætter det til 30, så vil en stikprøve på 40 kræve, at der er 1175 kunder den dag, og
det behøver jo ikke at være tilfældet. Omvendt hvis tallet er for lille, så får man måske udtaget
de 40 kunder i løbet af formiddagen, og så er stikprøven nok ikke repræsentativ, da man ikke får
eftermiddagskunderne med.
38

5.2 Fordeling og spredning af gennemsnit
Klyngeudvælgelse (Cluster sampling)
Denne metode kan med fordel benyttes, hvis populationen består af eller kan inddeles i
delmængder (klynger) . Metoden består i, at man ved randomisering vælger et mindre antal
klynger, som så totaltælles.
Eksempel: I et vareparti på 2000 emner fordelt på 200 kasser hver med 10 emner ønsker man en
vurdering af fejlprocenten.
Man udtager randomiseret 5 kasser, og undersøger alle emnerne i kasserne.
5.2. FORDELING OG SPREDNING AF GENNEMSNIT
Udtages en stikprøve fra en population er det jo for, at man ud fra stikprøven kan fortælle noget
centralt om hele populationen.
I eksempel 1.5 var vi således interesseret i koncentrationen af brintioner (pH) i ledvæsken i knæet
hos patienter, der led af denne sygdom.
Som led i en nordisk medicinsk undersøgelse udtog man blandt patienter der led af denne sygdom
tilfældigt en stikprøve på 75.
På basis heraf beregnede man gennemsnittet af pH værdierne til x = 7.2868 og spredningen
s = 0.134355 .
Man vil nu sige, at et estimat (skøn) for den “sande” middelværdi µ for hele populationen er 7.29
og den “sande” spredning” σ er 0.134.
Det er imidlertid klart, at disse tal er behæftet med en vis usikkerhed.
Havde vi valgt 75 andre patienter havde vi uden tvivl fået lidt andre tal.
Det er derfor ikke nok, at angive at den “sande” middelværdi er x , vi må også angive et
“usikkerhedsinterval”.
For at kunne beregne et sådant interval er det nødvendigt at kende fordelingen.
Her spiller den tidligere nævnte centrale grænseværdisætning en vigtig rolle, idet den jo (løst
sagt) siger, at selv om man ikke kender fordelingen af den kontinuerte stokastiske variabel, så vil
gennemsnittet af værdierne i en stikprøve på n tal vil være tilnærmelsesvis normalfordelt, hvis
blot n er tilstrækkelig stor ( i praksis over 30).
Dette er af stor praktisk betydning, idet det så ikke er så vigtigt, om selve populationen er
normalfordelt. Ofte er det jo kun af interesseret at kunne forudsige noget om hvor middelværdien
af fordelingen er placeret.
σ
Endvidere fremgik det af sætning 3.1 , at spredningen på x er σ(
x)
= , hvor σ er
n
spredningen på den enkelte værdi i stikprøven.
Heraf fremgår, at gennemsnittet kan man “stole” mere på end den enkelte måling, da den har en
mindre spredning.
39

5 Stikprøver
Eksempel 5.1. Fordeling af gennemsnit
Den tid, et kunde må venter i en lufthavn ved en check-in disk, er givet at være en stokastisk
variabel med en ukendt fordeling. Man har dog erfaring for, at ventetiden i middel er på 8.2
minutter med en spredning på 3 minutter.
Udtages en stikprøve på 50 kunder, ønskes fundet sandsynligheden for, at den gennemsnitlige
ventetid for disse kunder er mellem 7 og 9 minutter
Løsning:
Da antallet n i stikprøven på 50 er større end 30, kan vi antage at gennemsnittet er approksimativt
σ 3
normalfordelt med en middelværdi på 8.2 og en spredning på σ = = = 0. 424
x
.
n 50
Vi har derfor
P( 7< X < 9)
=
TI89: normCdf(7,9,8.2,0.424) = 0.9681 = 96.8%
Excel: P( 7< X < 9) = P( X < 9) − P( X < 7)
=
NORMFORDELING(9;8,2;0,424;1)-NORMFORDELING(7;8,2;0,429;1) =0,9681 = 96.8%
5.3. KONFIDENSINTERVAL FOR MIDDELVÆRDI
5.3.1 Definition af konfidensinterval
Udtages en stikprøve fra en population er det jo for, at man ud fra stikprøven kan fortælle noget
centralt om hele populationen.
Man vil eksempelvis beregne gennemsnittet x og angive det som et estimat (skøn) for den
“sande” middelværdi µ for hele populationen
Det er imidlertid klart, at selv om et gennemsnit har en mindre spredning end den enkelte måling,
så er det stadig behæftet med et vis usikkerhed
Det er derfor ikke nok, at angive at den “sande” middelværdi er x , vi må også angive et
“usikkerhedsinterval”.
Et interval indenfor hvilket den “sande værdi” µ med eksempelvis 95% “sikkerhed” vil ligge,
kaldes et 95% konfidensinterval for middelværdien.
Mere præcist gælder det, at hvis man for et stort antal stikprøver på den samme stokastiske
variabel angav 95% konfidensintervaller, så ville den sande middelværdi tilhøre 95% af disse
intervaller. 1
1
Præcis definition af konfidensinterval. Lad være givet en stikprøve for en stokastisk variabel X, lad være et tal
mellem 0 og 1. Lad endvidere Θ være en punktestimator for parameteren θ og lad L og U være stokastiske variable,
for hvilke det gælder, at PL ( ≤θ ≤ U)
= β . På basis af den givne stikprøve findes tal l og u som bestemmer det ønskede
interval l ≤θ≤u. Dette kaldes et 100 ⋅ β procent konfidensinterval for den ukendte parameter θ .
40
β

5.3.2. Populationens spredning kendt eksakt
Et 95% konfidensinterval [ x − r; x + r]
må ligge symmetrisk
omkring gennemsnittet, og således, at
Px ( −r≤ X≤ x+ r)
= 095 . .
Heraf følger, at hvis den sande middelværdi µ ligger i et af
de farvede områder på figur 5.1, så er der mindre end 2.5%
chance for, at vi ville have fået det fundne gennemsnit x .
For at finde grænsen for intervallet, må vi finde en middelværdi
µ så P( X ≤ x)
= 0. 025 .
Man kan vise, at der gælder følgende formel
5.3 Konfidensinterval for middelværdi
2
I celle A1 skrives en startværdi for µ eksempelvis 90. I celle B1 skrives
=NORMFORDELING(90;A1;0,5/0.1443;1) Funktioner “Målsøgning” I “Angiv celle” skrives B1. I “Til
Værdi” skrives 0,025. I “Ved ændring af celle” skrives A1. Resultat 90,2841
41
x − r x x + r
Fig 5.1. 95% konfidensinterval
Er spredningen eksakt kendt er et 95% konfidensinterval bestemt ved formlen
σ
σ
x −u0. 975 ⋅ ≤ µ ≤ x + u0.
975 ⋅
(1)
n
n
Forklaring på formel for 95% konfidensinterval
Lad gennemsnittet af 12 målinger være x = 90 , og lad os antage, at spredningen kendes eksakt
til σ = 0.5.
σ 05 .
Vi ved, at spredningen på gennemsnittet er “standardfejlen” σ(
X ) = = = 01443 . .
n 12
Hvis den sande middelværdi µ afviger stærkt fra 90 er det yderst usandsynligt, at vi ville have fået
et gennemsnittet på 90.
Eksempelvis, hvis µ = 92 er P( X ≤ 90)
= 0.0000
TI89: P( X ≤ 90) = normCdf( −∞ ,90, 92, 0.1443) = 0
Excel: NORMFORDELING(90;92;0,5/KVROD(12);1) = 0
P( X ≤ 90)
=
dvs. det er ganske usandsynligt at den sande middelværdi var 92.
For at finde grænsen kunne man finde µ af ligningen PX ( ≤ 90) = 0. 025
TI89: solve(normCdf ( −∞ ,90, x, 0.1443) =0.025,x) hvilket giver 90.283
Excel 2
Da der er symmetri omkring x
fås konfidensintervallet [89.717 ; 90.283]

5 Stikprøver
Lettere er det at benytte formlen xp = µ + up
⋅σ
som ved benyttelse af, at σ(
X ) =
σ
giver
n
µ = x −u0. 025 ⋅
σ
. Indsættes fra tabel 1 u0. 025 =−196
. (eller =NORMINV(0,025;0;1)) fås, at øvre
12
grænse for konfidensintervallet er µ = x + 196⋅
σ
= 90 + 196⋅ 12
= .
05
. .
.
90. 283
12
Da der er symmetri omkring x fås konfidensintervallet [89.717 ; 90.283]
Sædvanligvis udtrykkes de generelle formler ved signifikansniveauet α , som er sandsynligheden
for at begå en fejl . α sættes sædvanligvis til 10%, 5%, 1 % eller 0.1% svarende til henholdsvis
90%, 95%, 99% og 99.9% konfidensintervaller.
σ
σ
x −u x u
I så fald bliver formlen (udtrykt ved α ) α ⋅ ≤ µ ≤ + α ⋅
− n
− n
(2)
Eksempel 5.3. Konfidensinterval hvis spredningen er kendt eksakt
Lad os antage, at vi spredningen for en population kendes eksakt til σ = 58 ,
Bestem et 95% konfidensinterval for en stikprøve på 5 elementer, der har gennemsnittet x = 774 .
Løsning:
“Radius” r i et 95% konfidensinterval er r = u0975⋅
= 196⋅ =5.08
n n
58
σ .
. .
95% konfidensinterval: 774 . −508 . ≤ µ ≤ 774 . + 508 . ⇔266 . ≤ µ ≤1282
.
Lettere er det at finde konfidensintervallet ved at benytte
TI89: APPS STAT/LIST F7, 2: Z-Interval Vælg Stats Udfyld menuen med 5.8 7.74 osv.
Resultat [2.66 ; 12.82 ]
Excel: På værktøjslinien foroven: Tryk på = eller f x Vælg kategorien “Statistisk” Vælg “konfidensinter-
val” udfylde menuen : KONFIDENSINTERVAL(0,05;5,8;5)=5,08
95% konfidensinterval: 774 . −508 . ≤ µ ≤ 774 . + 508 . ⇔266 . ≤ µ ≤1282
.
Vi ved derfor med 95% “sikkerhed”, at populationens sande middelværdi ligger indenfor disse
intervaller 3 .
3
Mere præcist, at af de 100 stikprøver med tilhørende 95% konfidensintervaller, vil i middel kun 5 af disse
intervaller ikke indeholde den sande værdi.
42
1 2
1 2

43
5.3 Konfidensinterval for middelværdi
5.3.3. Populationens spredning ikke kendt eksakt
Sædvanligvis er populationens spredning σ jo ikke eksakt kendt, men man regner et estimat s
ud for den.
Da s jo også varierer fra stikprøve til stikprøve, giver dette en ekstra usikkerhed, så konfidensintervallet
for µ bliver bredere.
Hvis stikprøvestørrelsen er over 30 er denne usikkerhed dog uden væsentlig betydning, så i
sådanne tilfælde kan man i formel (1) (eller formel (2)) blot erstatte σ med s.
Er stikprøvestørrelsen under 30 bliver denne usikkerhed på s så stor, at man i formel (1) må
erstatte U- fraktilen med en såkaldt t - fraktil t0.975(f) (også benævnt ) hvor
u0975 . t0975 . , f
frihedsgradstallet f = n - 1, og n = antal målinger).
(eller udtrykt ved i formel (2) erstatte U- fraktilen med t - fraktilen t .)
α u
1− 2
α
Er spredningen ukendt er et 95 % konfidensinterval bestemt ved formlen:
x−t0, 975( n−1)
⋅
s
≤ µ
≤ x+ t0. 975(
n−1)
⋅
n
s
n
1− f
2
α ,
(eller udtrykt ved α x − t ⋅ ≤ µ ≤ x + t ⋅
(4)
s
n
α α
1− , n−1 1− , n−1
2
2
t-fordelinger
En t - fordeling har samme klokkeformede udseende som en U - fordeling (en normalfordeling
med middelværdi 0 og spredning 1)
I modsætning til U - fordelingen afhænger dens udseende imidlertid af antallet n af tal i
stikprøven.
Er frihedsgradstallet f = n -1 stort (over 30) er forskellen mellem en U- fordeling og en tfordeling
uden praktisk betydning.
Er f lille bliver t - fordelingen så meget bredere end U - fordelingen, at t-fordelingen må anvendes
i stedet for U-fordelingen.
Grafen viser tæthedsfunktionen for t-fordelingerne for f = 1, 5 og 30.
s
n
(3)

5 Stikprøver
Eksempel 5.4. Beregning af t-værdier.
1) Find t0. 975( 12)
og t0025 . ( 12)
.
2) Find P( X ≥ 1)
, hvor X er t - fordelt med 12 frihedsgrader.
Løsning:
TI-89:
1) t0. 975( 12)
= inv_t(0.975,12) = 2.18
t0025 . ( 12)
= inv_t(0.025,12) = -2.18
2) P( X ≥ 1) = tCdf(1, ∞ ,12) = 0.1685 = 16.85%
Excel:
f x
Der fremkommer en tabel med anvisning på, hvordan den skal udfyldes.
På værktøjslinien foroven: Tryk på = eller Vælg kategorien “Statistisk” Vælg “TINV”
Bemærk: TINV( α ; f) udregner den fraktil, der svarer til 1 -
Sætter vi således α = 5% fås t0975 . , dvs. der beregnes arealet af “øverste hale” hvilket jo også altid er det man
har brug for.
1) t0. 975( 12)
= TINV(0.05;12) = 2,178813
t 0. 025 ( 12)
= - 2,178813
2) =TFORDELING(1;12;1) = 0,168525
P( X ≥ 1)
Eksempel 5.5. Konfidensinterval, hvis spredningen ikke er kendt eksakt.
Ved fremstilling af et bestemt levnedsmiddel er det vigtigt, at et tilsætningsstof findes i
levnedsmidlet i en koncentration på 8.50 (g/l).
For at kontrollere dette udtager levnedsmiddelkontrollen 6 prøver af levnedsmidlet. Resultaterne
var:
Måling nr 1 2 3 4 5 6
koncentration x (g/l) 8.54 7.89 8.50 8.21 8.15 8.32
Idet man antager, på baggrund af tidligere lignende målinger, at resultaterne er normalfordelte,
skal man besvare følgende spørgsmål:.
a) Angiv et estimat for koncentrationens middelværdi og spredning.
b) Angiv et 95% konfidensinterval for koncentrationen, og vurder herudfra om kravet på 8.50
er opfyldt.
Løsning
Såvel TI89 som Excel har indbygget programmer, så man ikke behøver at anvende formlerne
direkte.
a) TI-89:
APPS Stat/List Indtast tal i en liste F7, 2: T-Interval Vælg Data Udfyld menuen
Resultater: x = 8268 . og s = 0241 . .
b) C Int :[ 802 . ; 852 . ]
Da intervallet indeholder 8.50, er kravet opfyldt, men da intervallet kun lige netop indeholder
tallet 8.50, så det vil nok være rimeligt, at foretage en ny vurdering på basis af nogle flere
målinger.
44
α
2

Excel: Data indtastes i cellerne A1 til A6
45
5.3 Konfidensinterval for middelværdi
Excel: 2003: Funktioner 2007: Data
derefter Dataanalyse Beskrivende statistik udfyld inputområde vælg Resumestatistik og konfidensniveau
Middelværdi 8,268333333
Standardfejl 0,098434976
Median 8,265
Tilstand #I/T
Standardafvigelse 0,241115463
Stikprøvevarians 0,058136667
Kurtosis -0,2376446
Skævhed -0,500530903
Område 0,65
Minimum 7,89
Maksimum 8,54
Sum 49,61
Antal 6
Konfidensniveau(95,0%) 0,25303516
a) Resultater: x = 8268 . og s = 0241 . .
b) 95% konfidensinterval: x ± r = 49. 086 ± r hvor r = 0.253
[8.268 -0.253 ; 8.268 + 0.253] =[8.02 ; 8.52]
Eksempel 5.6 Konfidensinterval, hvis originale data ikke kendt
Find konfidensintervallet for middelværdien , idet stikprøven er på 20 tal, som har et
µ
gennemsnit på 50 og en spredning på 12.
Løsning:
TI89:APPS Stat/List F7, 2: T-Interval Vælg Stats Udfyld menuen
C Int :[44.38 ; 55.62]
Excel : Har intet færdigt program, så her må man anvende formlen for konfidensinterval
I kolonne D er de formler angivet, som er brugt i kolonne E, men kolonne D er naturligvis
strengt taget unødvendig.
A B C D E
1 Eksempel 4.6 Konfidensradius r = TINV(B6;B3-1)*B5/KVROD(B3) = 5,616173
2 nedre grænse = B4-E1 44,38383
3 n = 20 øvre grænse = B4+E1 55,61617
4 gennemsnit = 50
5 spredning s = 12
6 Signifikansniveau " = 0,05
95% konfidensinterval: [44.38 ; 55.62]

5 Stikprøver
Prædistinationsinterval. Ved mange anvendelser ønsker man at forudsige, hvor værdien af
en kommende observation af den variable med 95%”sikkerhed” vil falde, snarere end at give
et 95% konfidensinterval for middelværdien af den variable. Man siger, at man ønsker at
bestemme et 95% prædistinationsinterval (forudsigelsesinterval).
SÆTNING 4.2 ( 100 ⋅ ( 1 − α ) % prædiktionsinterval for en enkelt observation ).
Et 100 ⋅( 1 −α)
% prædiktionsinterval for en enkelt fremtidig observation Xn+1 er bestemt ved
X n+1
Bevis: Lad være en enkelt fremtidig observation. Eftersom er uafhængig af de øvrige X’er, er
X n+1 også uafhængig af X .
2
σ 2 2
Variansen af differensen X − Xn+1er følgelig V( X − Xn ) = V( X) + V( Xn
) = + =
⎛ 1
⎜ +
⎞
+ 1 + 1 σ σ 1 ⎟ .
n ⎝ n⎠
Da man sædvanligvis først regner konfidensintervallet ud, så er den nemmeste måde at
beregne det tilsvarende prædistinationsinterval at benytte, at radius rp i prædistinationsinterval
fås af radius rk i konfidensintervallet ved formlen r = r ⋅ 1+
n
46
p k
Bevis: r s s
n
n 1 + 1 1+
n s
p = ⋅ 1+ = = s = 1+ n = rk1+ n
n n n
Eksempel 5.7. Prædistinations-interval for middelværdi af normalfordeling.
Samme problem som i eksempel 5.5, men nu ønskes bestemt et 95% prædistinationsinterval
for en enkelt ny måling af koncentrationen.
Løsning
Da konfidensintervallet har længden 8.52 - 8.02 = 0.50 er radius rk = 0.25
Vi har derfor rp= 025 . ⋅ 6+ 1= 066 . og dermed
95% konfidensinterval = 827 . − 066 . ; 827 . + 066 . == 761 . ; 893 . .
X n+1
[ ] [ ]
Bestemmelse af stikprøvens størrelse
Før man starter sine målinger, kunne det være nyttigt på forhånd at vide nogenlunde hvor
mange målinger man skal foretage, for at få resultat med en given nøjagtighed.
Hvis spredningen antages kendt , ved vi, at radius i konfidensintevallet er
σ
r = u α ⋅
− n
1 2
Løses denne ligning med hensyn til n fås
⎛ u
⎜
n = ⎜
⎜
⎝
2
α ⋅σ
1− 2
r
1
1
x −t α ( n−1) ⋅s⋅ 1+
≤ µ ≤ x + t α ( n−1) ⋅s⋅ 1+
.
− n
−
n
⎞
⎟
⎟
⎟
⎠
1 2
1 2

47
5.3 Konfidensinterval for middelværdi
Det grundlæggende problem er her, at man næppe kender spredningen eksakt.
Man kender muligvis på basis af tidligere erfaringer størrelsesordenen af spredningen. Hvis
ikke må man eventuelt lave nogle få målinger, og beregne et s på basis heraf.
Som en første tilnærmelse antages, at antallet af gentagelser n er over 30, så man kan bruge Ufordelingen.
Hvis det derved viser sig, at n er under 30 anvendes i stedet en t-fordeling, idet vi løser
ligningen
⎛ t α ( n−1)
⋅σ⎞
⎜ 1− 2 ⎟
n = ⎜
⎟
⎜ r ⎟
⎝
⎠
Det følgende eksempel illustrerer fremgangsmåden.
Eksempel 5.8. Bestemmelse af stikprøvens størrelse.
En forstmand er interesseret i at bestemme middelværdien af diameteren af voksne egetræer i
en bestemt fredet skov.
Der blev målt diameteren på 7 tilfældigt udvalgte egetræer (i 1 meters højde over jorden)
På basis af målingerne på de 7 træer sættes s ≈ 14 .
a) Find hvor mange træer der skal måles, hvis et 95% konfidensinterval højst skal have en
radius på ca. 5 cm.
b) Find hvor mange træer der skal måles, hvis et 95% konfidensinterval højst skal have en
radius på ca. 6 cm.
Løsning:
a) Da = 196 . fås
u0975 .
2 2
⎛ u0975 . ⋅ s⎞⎛196
. ⋅14⎞
n = ⎜ ⎟ = ⎜ ⎟ ≈ 31
⎝ r ⎠ ⎝ 5 ⎠
TI89: (invNorm(0.975)*14)/5)^2 = 30.1 = 31
Excel: (NORMINV(0,975;0;1)*14/5)^2 = 30.1
Da n > 30 er det rimeligt, at benytte en U- fordeling frem for en t-fordeling.
Der skal altså tilfældigt udvælges ca. 32 egetræer.
2 2
⎛ u0975 . ⋅ s⎞
b)
⎛ 196 . ⋅14⎞
n = ⎜ ⎟ = ⎜ ⎟ ≈ 21
⎝ r ⎠ ⎝ 6 ⎠
2
⎛ t0975 . n− ⋅s
Da n < 30 burde man have anvendt en t - fordeling. ,( 1)
⎞
n = ⎜
⎟
⎝ r ⎠
TI 89: solve(x=(invt(0.975,x-1)*14/6)^2,x) x>21
Efter nogen tid fås x = 23.37
Excel: I celle A1 skrives en startværdi for n eksempelvis 21.
I celle B1 skrives= (TINV(0,05;A1)*14/6)^2-A1
2003: Funktioner “Målsøgning”
2007: Data Hvad-hvis analyse ”Målsøgning
I “Angiv celle” skrives B1. I “Til Værdi” skrives 0. I “Ved ændring af celle” skrives A1. Facit :23,29865
Der skal altså tilfældigt udvælges ca. 24 egetræer.
2

5 Stikprøver
Da overslaget jo er afhængigt af om vurderingen af s er korrekt, bør man dels for en
sikkerheds skyld vælge s lidt rigelig stor, dels efter at man har målt de 31/24 træer lige
kontrollere beregningen af konfidensintervallet.
5.4 KONFIDENSINTERVAL FOR SPREDNING
I visse situationer ønsker man at finde et konfidensinterval for spredningen.
Vi vil ikke gå nærmere ind på teorien herfor, men blot henvise til formlerne i appendix 5.1.
2
2
( n−1) s 2 ( n−1) s
Formel 4 i appendix 5.1 benyttes:
≤σ≤ 2
2
χ ( n −1)
χ ( n −1)
χ 2
1
Definition af -fordelingen. Lad U1, U2,..., U f være uafhængige normerede normalfor-delte variable.
Sandsynlighedsfordelingen for den stokastiske variabel χ kaldes -fordelingen med
2 2 2 2
= U1+ U2+ ,..., U f χ 2
frihedsgradstallet f og betegnes χ 2 ( f )
α α
1− 2
2
I formlerne indgår den såkaldte χ - fordeling, (udtales ki i anden) .
2
χ 2
-fordelinger
χ -fordelingen benyttes ved beregninger omkring varianser, når disse er erstattet af et
2
estimat s 2 . 1
På figuren er afbildet tæthedsfunktionen for χ - fordelingerne , og .
2
χ 2 () 5 χ 2 ( 10)
χ 2 ( 20)
Det ses, at χ kun er defineret for tal større end eller lig nul, og at -fordelinger ikke er
2
χ 2
symmetriske om middelværdien. Jo større frihedsgradstallet bliver jo mere symmetriske bliver
de dog, og for store f - værdier - i praksis f > 30 - kan en χ -fordeling approksimeres
2
χ 2 ( f )
med normalfordelingen n( µ , σ ), hvor µ = f og σ = 2 ⋅ f .
TI89 og Excel har en kumuleret - fordeling ligesom naturligvis alle statistikprogrammer
χ 2
har det.
48

Eksempel 5.9. Beregning af χ - værdier.
2
2
2
1) Find χ0. 025()
8 og χ 0. 975()
8 .
2) Find P( X ≤ 5)
,
hvor X er χ - fordelt med 8 frihedsgrader.
2
Løsning:
2
TI89: 1) χ0. 025()
8 =invChi2(0.025, 8) = 2.18
2
χ 0. 975()
8 =invChi2(0.975, 8) = 17.5
(se det skraverede areal på figuren)
2) P( X ≤ 5)
= chi2Cdf(0, 5, 8) = 0.242
2
Excel:1) χ0. 025()
8 =CHIINV(0,975;8)=2.18
2
χ 0. 975()
8 =CHIINV(0,025;8)=17.5
P( X ≤ 5)
2) =1-CHIFORDELING(5;8) = 0.242
Bemærk Excel beregner den “øvre hale”
49
5.4 konfidensinterval for spredningen
Eksempel 5.10. Konfidensinterval for varians og spredning af normalfordeling.
En virksomhed ønsker at kontrollere med hvilken spredning en bestemt målemetode angiver
saltindholdet i en opløsning. Der foretages følgende 12 målinger af en opløsning af det
pågældende salt. Resultaterne var:
Måling nr 1 2 3 4 5 6 7 8 9 10 11 12
% opløsning 6.8 6.0 6.4 6.6 6.8 6.1 6.4 6.3 6.0 6.2 5.8 6.2
a) Angiv på basis af måleresultaterne et estimat for opløsningens spredning.
b) Angiv et 95% konfidensinterval for variansen og for spredningen.
Løsning:
TI-89 og Excel har intet færdigt program.
2
2
( n−1) s 2 ( n−1) s
Begge må anvende formel 4 i appendix 5.1 :
≤σ≤ 2
2
χ ( n −1)
χ ( n −1)
α α
1− 2
2
TI89: a) Data indtastes i list 1 F4 1 var Stats menu udfyldes
b)
Vi finder s = 0.3162 .
Nedre grænse: (11*0.3162^2/ invChi2(0.975,11) = 0.0502
Øvre grænse : (11*0.3162^2/ invChi2(0.025,11) = 0.288
2
0. 0502 ≤σ≤0. 288 . 0. 0502 ≤σ ≤ 0. 2880 ⇔ 0. 2241≤σ ≤05366
. .
Excel: a) Data indtastes i cellerne A1 til A12
På værktøjslinien foroven: Tryk på f x Vælg kategorien “Statistisk” Vælg “STDAFV”
Tabel udfyldes: s =STDAFV(A1:A7)= 0,316228
b) Lad s være gemt i A14
Nedre grænse := (12-1)*A14^2/CHIINV(0,025;11) = 0,050182 gemt i A16
Øvre grænse: =(12-1)*A14^2/CHIINV(0,975;11) = 0,288279 gemt i A 17
95% konfidensinterval for variansen: [0.0502 ; 0.288]
95% konfidensinterval for spredningen:
KVROD(A16) = 0.2241 KVROD(A17) =0.5366
95% konfidensinterval for spredningen:[0.2241 ; 0.5366]

5 Stikprøver
5.5. OVERSIGT over centrale formler i kapitel 5
n( µ , σ )
x
X antages normalfordelt .Givet stikprøve af størrelsen n med gennemsnit og spredning s
Oversigt over konfidensintervaller
nr Forudsætninger Estimat for parameter 100 (1 - α ) % konfidensinterval for parameter
1
2
3
4
µ ukendt.
σ kendt
µ ukendt.
σ ukendt
µ kendt
σ ukendt.
µ ukendt
σ ukendt.
For µ : x
For µ : x
For σ :
2
n − 1 s + n x −
n
2 ( ) ( µ )
s µ =
For σ :
2 s 2
2 2
Oversigt over prædistinationsintervaller
σ
σ
x −u α ⋅ ≤ µ ≤ x + u α ⋅
− n
− n
50
1 2
1 2
TI89 :F7: Z-interval
Excel: Konfidensinterval (= radius)
s
x −t α ( n−1)
⋅ ≤ µ ≤ x + t α ( n−1)
⋅
− n
−
1 2
1 2
TI89 :F7: t-interval
Excel: Konfidensniveau (= radius)
2 2
( n − 1) s + n( x − µ ) 2 ( n − 1)
s + n( x − µ )
2
≤ σ ≤
2
χ ( n)
χ ( n)
α α
1− 2
2
2
2
( n − 1)
s 2 ( n − 1)
s
2 ≤ σ ≤ 2
χ ( n − 1)
χ ( n − 1)
α α
1− 2
2
2 2
nr Forudsætninger Estimat for parameter 100 (1 - α ) % konfidensinterval for parameter
1
2
µ ukendt.
σ kendt
µ ukendt.
σ ukendt
For µ : x
For µ : x
σ
radius i konfidensinterval rk = u α ⋅
− n
1 2
radius i prædistinationsinterval r = r 1+
n
p k
radius i konfidensinterval rk = t α ( n−1)
⋅
1− 2
s
n
radius i prædistinationsinterval r = r 1+
n
p k
Bestemmelse af stikprøvens størrelse n.
Ønsket værdi af radius r i 100 (1 - α ) % konfidensinterval konfideninterval
1
2
σ kendt
eller n > 30
σ ukendt, men antag
den højst er s n
⎛ u
⎜
n = ⎜
⎜
⎝
2
α ⋅σ
⎞
TI89: (invNorm(1- α /2)* σ /r)^2
⎟ Excel:(NORMINV(1- α /2);0;1)* σ /r)^2
⎟
r ⎟
⎠
1− 2
2
⎛ t α ( n−1) ⋅s⎞
Løs ligning , se eksempel 5.8
⎜ 1− 2 ⎟
= ⎜
⎟
⎜ r ⎟
⎝
⎠
s
n

OPGAVER
51
Opgaver til kapitel 5
Opgave 5.1
Lad der være givet 10 uafhængige observationer af en syres koncentration (i %).
12.4 10.8 12.1 12.0 13.2 12.6 11.5 11.9 12.8 12.0
1) Find et estimat for koncentrationens middelværdi µ og spredning σ .
2) Angiv et 95% konfidensinterval for µ .
3) Angiv et 95% prædistinationsinterval for en enkelt ny måling af koncentrationen..
4) Angiv et 95% konfidensinterval for µ , idet det antages, at man fra tidligere målinger ved,
at σ = 0.65.
Opgave 5.2
Trykstyrken i beton blev kontrolleret ved at man støbte 12 betonklodser og testede dem.
Resultatet var:
2216 2225 2318 2237 2301 2255 2249 2281 2275 2204 2263 2295
1) Find et estimat for trykstyrkens middelværdi µ og spredning σ .
2) Angiv et 95% konfidensinterval for µ .
3) Angiv et 95% prædistinationsinterval for en enkelt måling af trykstyrken på en ny
betonklods.
4) Man fandt, at radius i konfidensintervallet var for stor.
Bestem med tilnærmelse antallet af målinger der skal udføres, hvis radius højst skal være
15.
Opgave 5.3
En fabrik producerer stempelringe til en bilmotor. Det vides, at stempelringenes diameter er
approksimativt normalfordelt. Stempelringene bør have en diameter på 74.036 mm og en
spredning på 0.001 mm. For at kontrollere dette udtog man tilfældigt 15 stempelringe af
produktionen og målte diameteren. I resultaterne har man for simpelheds skyld, kun angivet de
3 sidste cifre, altså 74.0365 angives som 365.
Man fandt følgende resultater
342 364 370 361 351 368 357 374 340 362 378 384 354 356 369
1) Find et estimat for ringenes diameter µ og spredning σ .
2) Angiv et 99% konfidensinterval for µ .
Opgave 5.4
En polymer produceres i batch. Viskositetsmålinger udført på hver batch gennem et stykke tid
har vist, at variationen i processen er meget stabil med spredning σ = 20.
På 15 batch gav viskositetsmålingerne følgende resultater:
724 718 776 760 745 759 795 756 742 740 761 749 739 747 742
1) Find et estimat for viskositetens middelværdi µ .
2) Angiv et 95% konfidensinterval for µ idet man antager spredningen er 20.
3) Find et estimat for viskositetens spredning σ .
4) Angiv et 95% konfidensinterval for σ , for at kontrollere påstanden om, at σ
= 20.

5 Stikprøver
Opgave 5.5
Ved en fabrikation af et bestemt sprængstof er det vigtigt, at en reaktoropløsning har en pHværdi
omkring 8.0. Der foretages 6 målinger på en bestemt reaktantopløsning.
Resultaterne var:
pH 8.42 7.36 8.04 7.71 7.65 7.82
Den benyttede pH-målemetode antages på baggrund af tidligere lignende målinger at give
normalfordelte resultater.
1) Angiv et estimat for opløsningens middelværdi og spredning.
2) Angiv et 95% konfidensinterval for pH.
3) Man finder, at radius i konfidensintervallet er for bredt.
Angiv med tilnærmelse antallet af målinger der skal foretages, hvis radius skal være 0.1.
Opgave 5.6
Samme tal som i opgave 5.2
Find et 95% konfidensinterval for trykprøvens spredning.
Opgave 5.7
Samme tal som i opgave 5.3
Find ud fra stikprøven et 99% konfidensinterval for diameterens spredning.
Opgave 5.8
De 10 øverste ark papir i en pakke med printerpapir har følgende vægt
4.21 4.33 4.26 4.27 4.19 4.30 4.24 4.24 4.28 4.24
a) Angiv et 95%-konfidensinterval for middelværdi af papirets vægt.
b) Angiv med tilnærmelse antallet af ark, der skal anvendes, hvis radius i konfidensintervallet
højst skal være r = 0.02
c) Angiv et 95%-prædistinationsinterval for en enkelt nyt ark papir.
d) Angiv et 95%-konfidensinterval for spredningen af papirets vægt.
Opgave 5.9
Til undersøgelse af alkoholprocenten i en persons blod foretages 4 uafhængige målinger, som
gav følgende resultater (i ‰):
108 102 107 98
1) Opstil et 95% konfidensinterval for personens alkoholkoncentration.
2) Opstil et 95% konfidensinterval for målemetodens spredning.
52

53
6.1 Grundlæggende begreber
6 HYPOTESETEST
(ÉN NORMALFORDELT VARIABEL)
6.1 GRUNDLÆGGENDE BEGREBER
Ofte vil man se vendinger som” Stikprøven viser, at udbyttet ved den ny metode er signifikant
større end ved den hidtidig anvendte metode”
Statistiske problemer, hvor man på basis af en stikprøve ønsker med eksempelvis 95% “sikkerhed”
at bevise en påstand om hele populationen kaldes hypotesetest.
De forskellige begreber der indgår i en hypotesetest vil blive gennemgået i forbindelse med
følgende eksempel.
Eksempel 6.1. Hypotesetest.
En fabrik har gennem mange år benyttet en metode, der på basis af en given mængde råmateriale
gav et middeludbytte af et produceret stof på µ 0 = 69.2 kg og spredningen σ = 1.0 kg.
En nyansat ingeniør får til opgave at søge at forøge middeludbyttet ved en passende (billig)
modifikation af procesbetingelserne.
Efter en række lovende eksperimenter i laboratoriet synes opgaven at være lykkedes, men det
endelige bevis herfor er, ud fra et passende antal driftsforsøg statistisk at kunne “bevise”, at
middeludbyttet er blevet forøget.
Ud fra kendskab til de forskellige mulige støjfaktorer antages spredningen at være uændret på
1.0 kg.
Da driftsforsøgene er meget ressourcekrævende, bevilges der kun 12 delforsøg.
Der foretages 12 uafhængige delforsøg og udbyttet x måltes:
Forsøg nr 1 2 3 4 5 6 7 8 9 10 11 12
x 68.8 70.7 70.3 70.1 70.7 68.7 69.2 68.9 70.0 69.6 71.0 69.1
1) Kan man ud fra disse data bevise på signifikansniveau α = 0.05 , at middeludbyttet er blevet
forøget ?
2) Hvis svaret i spørgsmål 1 er bekræftende, så angiv et estimat for det nye middeludbytte, og
angiv et 95% konfidensinterval herfor.

Hypotesetestning (1 normalfordelt variabel)
Løsning:
1) Løsningen opdeles for overskuelighedens skyld i en række trin
1a) Definition af stokastisk variabel X.
X = udbyttet ved den modificerede proces.
1b) Valg af X’s fordelingstype.
X antages at være approksimativt normalfordelt n( µ , 10 . ) .
1c) Opstilling af nulhypotese og alternativ hypotese.
Der opstilles en såkaldt Nulhypotesen H0 : µ = 69.2 kg.
Nulhypotesen skal indeholde en konkret påstand (her et lighedstegn). Påstanden er, at
modifikationen ingen (nul) virkning har
Der opstilles endvidere en alternativ hypotese H: µ > 69.2 kg.
Den alternative hypotese skal så vidt muligt indeholde det, der ønskes bevist. I dette
tilfælde ønskes vist, at middeludbyttet er vokset, dvs. µ > 69.2 kg.
Testen kaldes en ensidet test i modsætning til en tosidet test :
H0 : µ = 69.2 kg contra H: µ ≠ 69.2 kg,
hvor vi blot ønsker at vise, at middeludbyttet har ændret sig.
1d) Angivelse af testens signifikansniveau.
Hvis stikprøvens gennemsnit x er meget større end 69.2 kg ( måske helt op mod 100
kg), så er der stor sandsynlighed for at udbyttet er steget. Man siger så, at nulhypotesen
forkastes, eller at x ligger i forkastelsesområdet (se figur 6.1).
Hvis derimod x kun ligger lidt over 69.2 kg, så kan det skyldes tilfældige udsving, og
man kan ikke med nogen stor sikkerhed konkludere, at udbyttet er steget. Man siger, at
nulhypotesen accepteres, eller at x ligger i acceptområdet.
x 0
Fig. 6.1 Accept- og forkastelsesområde
Lad være grænsen mellem acceptområdet og forkastelsesområdet. skal bestemmes
sådan, at forudsat H0 : µ = 69.2 kg er sand, så er det yderst usandsynligt, at en
stikprøves gennemsnit x vil komme til at ligge i forkastelsesområdet. Hvis stikprøvens
gennemsnit alligevel ligger i forkastelsesområdet, må det være forudsætningen H0 der
er forkert, d.v.s. middeludbyttet må være blevet større.
Det er naturligvis ikke entydigt bestemt, hvad det vil sige, at noget er yderst usandsynligt.
Man starter derfor enhver test med at fastlægge det såkaldte signifikansniveau α .
Er α valgt til 5% ,så har man derved fastlagt, at sandsynligheden for fejlagtigt at
påstå, at middeludbyttet er steget, er under 5%.
Da det kan have alvorlige økonomiske konsekvenser fejlagtigt at påstå at middeludbyttet
54
x 0

Fig 6.2 P-værdi
55
6.1 Grundlæggende begreber
er steget (produktionen omstilles osv.) ,så er man naturligvis interesseret i, at dette ikke
sker.
Det normale i industriel produktion er, at sætte α = 5%, men er det eksempelvis medi-
cinske forsøg, hvor det kan have alvorlige menneskelige konsekvenser, sættes α måske
så lavt som 1% eller 0.1%, mens man i andre situationer måske sætter signifikansniveauet
til 10%.
I dette eksempel er α sat til 5%.
1e) Beregning af P - værdi
Gennemsnittet af de 12 resultater giver x = 69.76 kg.
Under forudsætning af at nulhypotesen H0 : µ = 69.2 kg er sand, så er X er normalforσ
10 .
delt med middelværdi µ 0 = 69.2 og spredning = = 0. 2887 .
n 12
Vi kan derfor nemt finde den præcise adskillelse mellem accept og forkastelsesområdet,
da den jo er bestemt ved at arealet skal være 95%
TI89: invNorm(0.95,69.2,1.0/12)= 69.67
Da 69.76 > 69.76 ligger det målte gennemsnit altså i forkastelsesområdet.
Imidlertid vælger man i stedet at beregne den såkaldte P-værdi (Probability value) som
er sandsynligheden for at få en værdi på det fundne stikprøvegennemsnit 69.76 eller
derover, dvs. P-værdi = P( X ≥ 69. 76)
Er denne P-værdi er mindre end α =0.05 må x = 69.76 ligge i forkastelsesområdet (se
figur 6.2)
Hvis P-værdien ligger over α ligger x = 69.76 i acceptområdet, dvs. vi kan ikke bevise
at middeludbyttet er steget.
TI89: P - værdi = normCdf(69.76, 6921 12 =0.0262
P( X ≥ 69. 76) =
∞, . , / ( ))
Excel: P - værdi = 1-NORMFORDELING(69,76;69,2;1/KVROD(12);1)=0,026196
P( X ≥ 69. 76)
=
1f) Konklusion
Da P - værdi = 2.62% < 5% forkastes H0 ,
Vi har et statistisk bevis for, at den modificerede proces giver et større middeludbytte.

Hypotesetestning (1 normalfordelt variabel)
Alternativt kunne vi have benyttet nogle testfunktioner:
TI-89: APPS STAT/LIST data indtastes i list1 F6, 1: Z-Test
Menu udfyldes : µ 0 = 69. 2 , σ =1 , list =list1, Alternate Hyp: µ > µ 0 , Calculate
Excel: Data indtastes i A1 til A12 fx Statistisk Z-test ZTEST(A1:A12;69,2;1)
Vi får i begge tilfælde P-værdi = 0.0265, dvs. samme værdi som før.
2) Udbyttet kan i middel forventes at være ca. x = 69. 76 kg
99% konfidensinterval:
TI-89: APPS STAT/LIST data indtastes i list1 F7, 2: Z-Interval C Int : [ 6919 . ; 70. 32]
Excel: f x Statistisk konfidensinterval KONFIDENSINTERVAL(0,05;1;12) 0,565793
[69.76 - 0.57;69.76+0.57] = [69.19 ; 70.32]
At konfidensintervallet indeholder tallet 69.2 er klart i modstrid med at vi lige har vist, at
middelværdien er større end 69.2.
Det skyldes, at konfidensintervallet forkaster med 2.5% til hver side, mens en ensidet test
forkaster kun til en side med 5%.
Mere logisk ville det være, at lave en ensidet 95% konfidensinterval,
⎡
⎤ ⎡
⎤
⎢x
−u095⋅ ∞⎥
= ⎢69
76 −165⋅ ∞⎥
= [ ∞]
⎣ n ⎦ ⎣
⎦
10
σ
.
. ; . . ; 69. 28;
12
Det er imidlertid ikke standard, nok fordi det er sværere at forklare en udenforstående, at
middelværdien med 95% sikkerhed ligger over 69.28 .
Eksempel 6.2. Hypotesetest, hvor man får accept af H0. Samme problem som i eksempel 6.1, men nu er signifikansniveauet α =1%.
Løsning:
H0: µ = 69.2 mod H: H0: µ > 69.2
I eksemplet fandt vi på basis af 12 forsøg, at P-værdi = 2.6%.
Konklusion: H0 accepteres , dvs.
vi kan ikke på et signifikansniveau på 1% bevise, at middelværdien var steget.
Bemærk: Vi skriver ikke at vi har bevist den ikke er steget, det kan meget vel være tilfældet.
Vi kan bare ikke bevise det med den ønskede sikkerhed.
56

6.2 Eksempler på hypotesetest regnet med TI89 og Excel
6.2 EKSEMPLER PÅ HYPOTESETEST REGNET MED TI89 OG EXCEL
I eksempel 6.1 blev baggrunden for testen gennemgået. Samtidig antog vi, at spredningen var
kendt eksakt. Dette er sjældent tilfældet, men havde vi haft over 30 målinger i stikprøven, ville
det være tilladeligt, at erstatte den eksakte værdi med den beregnede spredning s, og foretage de
samme beregninger
Havde vi under 30 målinger bliver det for upræcist, og man må i stedet benytte en t-fordeling.
Eksempel 6.2. Ensidet hypotesetest om middelværdi (spredning ikke kendt eksakt)
Samme problem som i eksempel 6.1, men nu er spredningen ikke kendt eksakt.
Løsning:
1) X = udbyttet ved den modificerede proces.
X antages at være approksimativt normalfordelt n( µ , 10 . ) .
H0 : µ = 69.2 kg. H: µ > 69.2 kg.
Beregning
TI89: APPS STAT/LIST data indtastes i list1 F6, 2: T-Test
Menu udfyldes : = 69. 2 , list =list1, Alternate Hyp: µ µ , Calculate
µ 0
P-værdi = 0.0185 =1.85%.
Excel Her benyttes formlen i appendix 6.1.
( x − µ 0)
⋅ n
PT ( ≥ t)
, hvor t =
og T er t-fordelt med n -1 frihedsgrader
s
Data indtastes i A1 til A12
x streg = MIDDEL(A1:A12) 69,75833
s= STDAFV(A1:A12) 0,816265
Ho 0= 69,2
t= (E1-E3)*KVROD(12)/E2 2,369481
P-værdi= TFORDELING(ABS(E5);11;1) 0,018593
Da P-værdi < 5% forkastes H 0 , dvs. vi har et statistisk bevis for, at den modificerede proces
giver et større middeludbytte.
2) TI-89: APPS Stat/List F7, 2: T-Interval Vælg Data Udfyld menuen C Int :[69.24 ; 70.28]
Excel: 2003: Funktioner 2007: Data
Dataanalyse Beskrivende statistik udfyld inputområde vælg konfidensniveau
Resultat : Konfidensniveau(95,0%) 0,51863
Konfidensinterval [69.758-0.517;69.758-0.5179] = [69.24 ; 70.28]
57
> 0

Hypotesetestning (1 normalfordelt variabel)
Eksempel 6.3 Tosidet hypotesetest om middelværdi (spredning ikke kendt eksakt).
Ved fremstilling af et bestemt levnedsmiddel er det vigtigt, at et tilsætningsstof findes i
levnedsmidler i en koncentration på 8.40 (g/l).
For at kontrollere om tilsætningsstoffet har en koncentration på ca. 8.40, udtager levnedsmiddelkontrollen
6 prøver af levnedsmidler. Resultaterne var:
Måling nr 1 2 3 4 5 6 7 8
Koncentration x (g/l) 8.54 7.89 8.50 8.21 8.15 8.32 8.45 8.31
Det ønskes på denne baggrund undersøgt om koncentrationen har den ønskede værdi.
Signifikansniveau sættes til 5%.
Løsning:
Lad X være koncentrationen af tilsætningsstoffet i levnedsmidlet.
Det antages, at X er normalfordelt
n( µ , σ )
Da det både er uønsket, at koncentrationen er for lille og at den er for stor, bliver nulhypotesen
H0: µ = 8.4 mod H: µ ≠ 84 . , dvs. vi har en tosidet test.
Bemærk, at selv om man vel egentlig hellere ville bevise, at koncentrationen er 8.4 og derfor
helst ville have denne påstand i den alternative hypotese, er dette ikke muligt, da nulhypotesen
skal indeholde et lighedstegn.
TI-89: APPS STAT/LIST data indtastes i list1 F6, 2: T-Test
Menu udfyldes : µ 0 = 84 . , list =list1, Alternate Hyp: µ ≠ µ 0 , Calculate
Vi får P-værdi = 0.2117 =21.78%.
Da P-værdi > 5% accepteres nulhypotesen , dvs. vi kan ikke bevise, at koncentrationen
afviger signifikant fra 8.4 g/l
Bemærk, at TI-89 beregner begge “haler” , så vi skal sammenligne med 5% .
Excel Benytter formler i appendix 6.1
Data indtastes i A1 til A8
x streg = MIDDEL(A1:A8) 8,29625
s= STDAFV(A1:A8) 0,213537
Ho 0= 8,4
n= 8
t= (E1‐E3)*KVROD(e4)/E2 ‐1,37423
P‐værdi= TFORDELING(ABS(E5);e4‐1;1) 0,105877
Da P-værdi > 2.5 % accepteres nulhypotesen , dvs. vi kan ikke bevise, at koncentrationen
afviger signifikant fra 8.4 g/l
Bemærk, at da det er en tosidet test hvor man forkaster til begge sider sammenlignes
med 2,5%
58

59
6.3 Fejl af type I og type II
Eksempel 6.7. Test af spredning
En fabrikant af læskedrikke har købt en automatisk “påfyldningsmaskine”.
Ved købet af maskinen har man betinget sig, at rumfanget af den påfyldte væske i middel skal
have en spredning, der ikke overstiger 0.20 ml.
Efter kort tids anvendelse får man mistanke om, at spredningen er for stor. Mange klager over
underfyldte flasker.
Derfor foretages en kontrol, hvor man tilfældigt udtager 20 flasker med læskedrik, og måler
rumfanget af væsken i flasken. Det viser sig, at stikprøvens spredning er s = 0.24 ml.
Med et signifikansniveau på 5% er det da et statistisk bevis for, at den nye maskine ikke opfylder
det stillede krav?
Løsning:
Lad X = rumfang af drik i flaske.
X antages normalfordelt n( µ , σ ) , hvor såvel µ som σ er ukendte.
Ho: σ = 02 . imod H: σ > 0.2,
eller udtrykt ved variansen σ :
2
2 2
2 2
Ho: σ = 02 . mod H: σ > 02 . .
Ifølge appendix 6.3 ses, at vi skal beregne teststørrelsen χ , hvor
2
2
2 ( n−1) ⋅s
χ =
dvs. i det foreliggende tilfælde χ .
2
σ
2
2
( 20 −1) ⋅0.
24
=
= 27. 36
2
02 .
0
TI 89: P- værdi = PQ ( ≥ 27. 36) = chiCdf(27.36, ∞ ,19) = 0.0965 = 9.65%
Excel:
chi i anden= (20-1)*0,24^2/0,2^2 27,36
P-værdi= CHIFORDELING(C1;19) 0,096543
Da P-værdi=9.65% > 5 %, accepteres H0 , dvs. det er ikke påvist, at spredningen ved påfyldningen
er for stor, men der er dog nær ved at være signifikans.
6.3. FEJL AF TYPE I OG TYPE II:
Ved enhver test kan der være to typer fejl, hvoraf vi hidtil kun har taget hensyn til den ene
type. For bedre at forstå problemstillingen vil vi se på følgende skema.
Beslutning
Forudsætning
H 0 accepteres H 0 forkastes
H 0 er sand Rigtig beslutning Forkert beslutning
Type I fejl
H 0 er falsk Forkert beslutning
Type II fejl
Rigtig beslutning
Det må være et krav til en god test, at der kun er en lille sandsynlighed for at begå en fejl af
type I eller type II.

Hypotesetestning (1 normalfordelt variabel)
I eksempel 6.1 ville en type I fejl være, hvis man konkluderer, at den modificerede proces
giver et større udbytte, selv om det ikke er tilfældet. Virksomheden bruger måske millionbeløb
på at omlægge produktionen, og det er ganske forgæves.
En type II fejl ville være, at man ikke opdager, at den modificerede proces giver et større udbytte.
Dette er naturligvis uheldigt, men hvis det skyldes, at forbedringen ikke blev opdaget,
fordi den er ganske ringe, har det muligvis ingen praktisk betydning.
Hvis en test har signifikansniveau α og den beregnede P-værdi < α så forkastes Ho .
Vi ved hermed, at P(type I fejl) ≤ α , dvs. vi rimelig sikre på, at have foretaget en korrekt
beslutning.
P-værdien angiver jo nogenlunde sandsynligheden for at vi træffer en forkert beslutning.
Hvis α = 5% og P-værdien er 4.25% forkastes H0. Det samme sker, hvis P-værdi = 0.001%,
men vi er her unægtelig noget sikrere på, at vi at vi træffer en korrekt beslutning.
Hvis vi accepterer H o er det blot udtryk for, at vi ikke kan forkaste(svag konklusion: "H o
frikendes på grund af bevisets stilling").
Man kan have begået en type II fejl, dvs. ikke opdaget, at den alternative hypotese var sand.
Eksempel 6.8. Fejl af type 2
Samme problem som i eksempel 6.1, men nu er signifikansniveauet α =1%
Løsning:
H0: µ = 69.2 mod H: H0: µ > 69.2
I eksemplet fandt vi på basis af 12 forsøg, at P-værdi = 2.6%.
Konklusion: H0 accepteres , dvs.
vi kan ikke på et signifikansniveau på 1% bevise, at middelværdien var steget.
Imidlertid kan middeludbyttet meget vel være steget, men vi kunne bare ikke bevise det med
den ønskede sikkerhed. Vi kan have begået en fejl af type 2.
Som det ses af eksempel 6.8, så vil en formindskelse af muligheden for at begå en type 1 fejl
( α formindskes) forøge sandsynligheden for at begå en type 2 fejl.
Den eneste måde hvorpå begge kan formindskes er at øge antallet n af forsøg.
Problemet hermed er, at man derved måske opdager en så lille forbedring, at det ikke er rentabelt
at foretage en dyr ændring af fremstillingsprocessen.
Først når udbyttet overstiger en bagatelgrænse ∆ vil man reagere.
Dimensionering af forsøg (vælge stikprøvestørrelse n).
Lad os antage, at virksomheden i eksempel 6.1 finder, at hvis stigningen i udbyttet ved den
modificerede proces er mindre end ∆ = 0.5 kg, så har det ingen praktisk interesse ( ∆ = 0.5
kg er bagatelgrænsen), og derfor gør det intet, hvis man ikke opdager det (begår en type II
fejl).
Hvis derimod stigningen ∆ er større end 0.5 kg, så har det stor betydning, og sandsynligheden
for at begå en type II fejl må derfor være lille. Lad os sætte den til højst β = 10%.
Problemet er nu, hvor stor en stikprøvestørrelse n (antallet af delforsøg) der skal udføres, for
at ovennævnte krav er opfyldt.
60

61
6.3 Fejl af type I og type II
En sådan vurdering kaldes en dimensionering af forsøget. Udfører man det ud fra en dimensionering
nødvendige antal forsøg, vil en accept af nulhypotesen nu betyde, at nok kan udbyttet
være steget, men ikke så meget, at det har praktisk interesse.
I appendix 6.1 og 6.2 er angivet de formler, der skal anvendes ved en dimensionering.
De følgende 2 eksempler viser anvendelsen heraf.
Eksempel 6.9. Dimensionering (kendt spredning).
Inden man i eksempel 6.1 begyndte at lave de dyre delforsøg, vil ingeniøren gerne have en
vurdering af, hvor mange driftsforsøg der er nødvendige, når det vides, at det først er økonomisk
rentabelt at gå over til den nye metode, hvis middeludbyttet er steget med mindst 0.5 kg.
1) Find stikprøvestørrelsen n, i det tilfælde, hvor ∆ = 0.5 kg og β = 10%.
Det antages stadig, at σ = 1.0 kg og signifikansniveauet er α = 5 %.
Lad n være den i spørgsmål 1 fundne stikprøvestørrelse.
2) Idet der udføres n delforsøg skal man besvare følgende spørgsmål:
a) Hvilken konklusion kan drages, hvis man finder, at x = 69.8
b) Hvilken konklusion kan drages, hvis man finder, at x = 69.4
Løsning
1) X = udbyttet ved den modificerede proces.
X antages at være approksimativt normalfordelt n( µ , 10 . ) .
H0 : µ = 69.2 kg. H: µ > 69.2 kg.
⎛ u1−α + u1−β ⎞ ⎛ u + u
Da testen er ensidet fremgår det af appendix 6.2) at: n ≥ ⎜ ⎟ = ⎜ 05 .
⎝ ⎠ ⎝
∆
σ
TI89: ((invNorm(0.95)+invNorm(0.90))/(0.5/1.0))^2 = 34.25 , dvs. n = 35 .
2
095 . 090 .
Excel: =((NORMINV(0,95;0;1)+NORMINV(0,9;0;1))/(0,5/0,1))^2 Resultat 0,342554 dvs. n = 35
2a) H0: µ = 69.2 mod H: H0: µ > 69.2
TI89: APPS STAT/LIST F6, 1: Z-Test Vælg Stats, da data ikke kendt
Menu udfyldes : µ 0 = 69. 2 , σ =1 , x = 69.8, n = 35, Alternate Hyp: µ > µ 0 , Calculate
P-værdi = 0.019%,
Excel: P-værdi = =1 - NORMFORDELING(69,8;69,2;1/KVROD(35);1) = 0,000193
Da P_værdi < 0.05 forkastes H0: µ = 69.2 kg , dvs. vi er på et Signifikansniveau på 5%
sikre på at middelværdien er over 69.2 kg.
Imidlertid kan vi ikke være sikre på at den er over bagatelgrænsen 69.2 + 0.5 = 69.7 kg
Lad H0: µ = 69.7 mod H: H0: µ > 69.7
Vi finder på samme måde som ovenfor, at P-værdi = 27.7%, dvs. en påstand om at middeludbyttet
ligger over 69.7 kg vil være fejlagtig i ca. 28% af tilfældene.
Vi vil derfor næppe på den baggrund gå over til den nye metode.
2b) H0: µ = 69.2 mod H: H0: µ > 69.2
Vi finder på samme måde som i punkt 2a) , at P-værdi = 11.8%%,
H0: µ = 69.2 kg accepters, dvs. vi kan ikke vise, at middeludbyttet er steget, men da vi
har dimensioneret er vi rimeligt sikre på, at en eventuel stigning ikke har praktisk interesse.
10 .
⎞
⎟
⎠
2

Hypotesetestning (1 normalfordelt variabel)
Eksempel 6.10. Dimensionering, (ukendt spredning)
En virksomhed bliver af miljøkontrollen pålagt at formindske indholdet i sit spildevand af et
stof A, der mistænkes for at kunne forurene grundvandet. Indholdet af stoffet A i spildevandet
skal under 1.7 mg/l, og miljøkontrollen henviser til en ny metode, som burde kunne formindske
indholdet til det ønskede niveau. For at vurdere den nye metode ønskes foretaget en række
delforsøg.
Hvor mange forsøg skal der mindst foretages, hvis α = 5%, β = 10%, ∆ = 0.10 mg/l og et
overslag over hvor stor σ er sætter denne til 0.15 mg/l.
Løsning:
Lad X = indhold af A (i mg/l) efter benyttelse af den ny metode.
X antages normalfordelt n( µ , σ ) , hvor såvel µ som σ er ukendte.
Da indholdet af stoffet A ønskes formindsket, bliver
nulhypotesen H0: µ = 17 . mg/l mod H: µ < 17 . mg/l, dvs. vi har en ensidet test.
Da σ ikke er kendt (kun et løst skøn kendes), er testen en t - test.
Formlen i appendix 6.1 anvendes:
2
⎛ u + u ⎞
Først beregnes 095 . 090 .
n ≥ ⎜ ⎟
∆
⎝ σ ⎠
TI89: ((invnorm(0.95)+invnorm(0.90))/(0.10/0.15))^2 Resultat n = 19.27
2
⎛ t095 . ( n−1)
⎞
Da n < 30 løses nu ligningen n = 19. 27⋅⎜
⎟
⎝ u095
. ⎠
solve(x = 19.27 ⋅ (inv_t(0.95,x-1)/invnorm(0.95))^2,x) x > 19
Heraf følger x = 21.17, dvs. n = 22
Den ønskede dimensionering kræver altså 22 forsøg.
Excel: ((NORMINV(0,95;0;1)+NORMINV(0,9;0;1))/(0,1/0,15))^2 Resultat n = 19.27
2
⎛ t095 . ( n−1)
⎞
Da n < 30 løses nu ligningen 19. 27⋅
⎜ ⎟ − n = 0
⎝ u ⎠
095 .
Resultatet 19.27 anbringes i celle A1
I celle B1 skrives som startværdi for n tallet 19 .
I celle C1 skrives =A1*(TINV(0,10;B1-1)/NORMINV(0,95;0;1))^2-B1
2003: Funktioner “Målsøgning”
2007: Data Hvad-hvis analyse ”Målsøgning
I “Angiv celle” skrives C1. I “Til Værdi” skrives 0.
“Ved ændring af celle” skrives B1
Resultat: I celle B1står 21,18523 dvs. n = 22
62

6.4. OVERSIGT over centrale formler i kapitel 6
n( µ , σ )
x
63
6.4 Oversigt
X antages normalfordelt .Givet stikprøve af størrelsen n med gennemsnit og spredning s
Signifikansniveau: α . er en given konstant
µ 0
Oversigt over test af middelværdi µ
T er en stokastisk variabel der er t - fordelt med f = n - 1.
σ
Y er en stokastisk variabel, der er normalfordelt n(
µ 0 ,
n
Forudsætninger Alternativ
hypotese H
σ ukendt.
( x − µ 0)
⋅ n
t =
.
s
σ kendt eks-
akt
P - værdi Beregning H 0 forkastes
H: µ > µ 0 PT ( ≥ t)
TI89: tCdf (, t ∞, n −1)
eller F6: t-test
Excel:tfordeling(t,n-1,1)
H: µ < µ 0 PT ( ≤ t)
TI89: tCdf ( −∞, t, n −1)
eller F6: t-test
Excel:1-tfordeling(t,n-1,1)
H: µ ≠ µ 0 PT ( ≥ t)
for x > µ 0
PT ( t)
for
som række 1
som række 2
H: µ > µ PY ( ≥ x)
0
H: µ < µ 0
H: µ ≠ µ 0
≤ x ≤ µ 0
PY ( ≤ x)
PY ( x)
for
≥ x > µ 0
PY ( x)
for
≤ x ≤ µ 0
σ
TI89: normCdf ( x,
∞ , µ 0 , )
n
eller F6: Z-test
⎛ σ
Excel:1-normfordeling x,
µ ,
eller ztest
⎜
⎝
0
⎞
⎟
n ⎠
⎛ σ ⎞
TI89: normCdf ⎜−∞,
x,
µ 0 , ⎟
⎝
n ⎠
eller F6: Z-test
⎛ σ ⎞
Excel:normfordeling x,
µ ,
eller ztest
som række 1
som række 2
⎜
⎝
0
⎟
n ⎠
P - værdi < α
P - værdi < 1
2 α
dog hvis t-test
P - værdi < α
P - værdi < α
P - værdi < 1
2 α
dog hvis Z-test
anvendes
P - værdi < α

Hypotesetestning (1 normalfordelt variabel)
Dimensionering
∆ = −
µ µ 0 µ
er den mindste ændring i der har praktisk interesse.
α =P(type I fejl), β = P(type II fejl)
Forudsætning Hypotese Formel Beregning
σ kendt eksakt
σ er ukendt,
men erstattes i
formlerne af
det bedste estimat
eller gæt
for spredningen.
Ensidet
Tosidet
⎛
⎜ u + u
n ≥ ⎜
⎜
∆
⎝ σ
1−α 1−β
⎛ u + u
⎜ 1− 2
n ≥ ⎜
⎜
∆
⎝ σ
α 1−
β
⎞
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎟
⎠
2
2
TI89: ((invNorm(1- α )+invNorm(1- β ))/( ∆ / σ ))^2
Excel: =((NORMINV(1- α ;0;1)+NORMINV(1- β ;0;1))/ ( ∆ / σ ))^2
TI89: ((invNorm(1- α /2)+invNorm(1- β ))/( ∆ / σ ))^2
Excel: =((NORMINV(1- α /2;0;1)+NORMINV(1- β ;0;1))/ ( ∆ / σ ))^2
Ensidet 2
Løse ligning, se eksempel 6.10
Tosidet
⎛ ⎞
⎜ u + u ⎟
1−α 1−β
⎛ t1−α( n−1)
⎞
n ≥ ⎜ ⎟ ⋅⎜
⎟
⎜ ∆
u
⎜
⎟ ⎝ 1−α
⎠
⎟
⎝ σ ⎠
⎛ u + u ⎞ t n
⎜ α 1−β
⎛
⎟ α ( −1)
⎞
1− ⎜ 1− ⎟
2
2
n ≥ ⎜ ⎟ ⋅⎜
⎟
⎜ ∆
u
⎜
⎟ ⎜ α ⎟
⎝ ⎠ ⎝ 1− σ
2 ⎠
2
64
2
2
Løse ligning, se eksempel 6.10

Oversigt over test af varians
χ 2
Q er fordelt med f = n - 1.
er en given konstant
σ 0
σ 2
65
6.4 Oversigt
Forudsætning Alternativ
hypotese H
P - værdi Beregning H0 forkastes
µ ukendt
2
H:σ
2
> σ0
2
PQ ( ≥ χ )
TI89:
2
chi2Cdf ( χ , ∞, n −1)
2
χ
2
( n − 1)
s
= 2
σ 0
2 2
H:σ < σ0PQ
( ≤ χ )
Excel: se eksempel 6.7 P-værdi< α
2 TI89:
2
chi2Cdf ( −∞, χ , n −1)
µ kendt
2 ( n − 1)
s + n( x − µ )
χ =
2
σ
2 2
0
2 2
H:σ ≠ σ PQ ( ≥ χ ) for
2
0
PQ ( ) for
≤ χ 2
2 2
H:σ > σ0PQ
( ≥ χ )
2 2
H:σ < σ0PQ
( )
2 2
H:σ ≠ σ PQ ( ≥ χ ) for
2
0
χ 2
χ 2
χ 2
≥ n −
< n −
1
1
som række 1
som række 2
2 TI89:
2
chi2Cdf ( χ , ∞,
n)
≤ χ 2 TI89:
≥ n −
1
PQ ( ≤ χ ) for
2
χ 2
< n −
1
P-værdi< 1
2 α
Excel: se eksempel 6.7 P-værdi< α
2
chi2Cdf ( −∞, χ , n)
som række 1
som række 2
P-værdi< 1
2 α

Hypotesetestning (1 normalfordelt variabel)
OPGAVER
Opgave 6.1
Et levnedsmiddel (“corned beef”) forhandles i pakker på 100 g.
Ved fabrikationen tilsættes traditionelt et konserveringsmiddel B (nitrit).
Da man har mistanke om, at B anvendt i større mængder kan have uønskede bivirkninger, må
der højst tilsættes 2.5 mg B pr. 100 g.
Fabrikanten reklamerer med, at der i middel højst er 2 mg B pr. pakke.
En konkurrent tvivler herpå, og vil teste påstanden.
Der købes i forskellige butikker i alt 36 pakker, og indholdet af B blev målt.
x
Man fandt et gennemsnit af B på = 2.10 mg med et estimat på spredningen på s = 0.30 mg
.
Kan man ud fra disse data bevise på signifikansniveau α = 0.01, at reklamen lyver.
Opgave 6.2
Et flyselskab overvejer at lukke en flyrute, såfremt µ = “middelværdien af antal solgte pladser
pr. afgang” er under 60.
På de sidste n = 100 afgange er der i gennemsnit solgt x = 58.0 pladser med en standardafvi-
gelse på s =11.0 pladser.
1) Kan man ud fra disse data bevise på signifikansniveau α = 0.05, at der i middel er solgt
under 60 pladser pr. afgang? (Husk at anføre: Hvad X er. Antagelser. Nulhypotese. Beregninger.
Konklusion.).
2) Angiv et estimat ~µ for middelværdien µ .
3) Forudsat, at man i spørgsmål 1 kan bevise, at der er solgt under 60 pladser, skal der angives
et 95% konfidensinterval for middelværdien µ .
Opgave 6.3
En fabrikation er baseret på en kemisk reaktion, hvor processen forudsætter tilstedeværelse af
en katalysator. Med den hidtil benyttede katalysatortype C1 udnyttes i middel kun ca. 70% af
den dyreste råvare. Firmaet overvejer at gå over til en mere effektiv katalysatortype C2 ved
produktionen. Omlægning hertil vil imidlertid kræve betydelige etableringsomkostninger,
hvorfor firmaet kun vil lægge produktionen om, såfremt i middel mindst 80% af den dyreste
råvare udnyttes, når C2 benyttes. Til vurdering heraf foretoges en række forsøg med benyttelse
af C2. Følgende udnyttelsesprocenter fandtes:
68.3 87.7 80.0 84.2 84.0 83.6 76.4 79.9 89.3 75.8
96.1 88.0 79.8 83.7 84.4 95.5 84.2 92.1 92.4 83.9
1) Lad X = udnyttelsesprocenten når C2 benyttes.
Beregn estimater x og s for middelværdi E(X) og spredning σ ( X ) .
2) Vurder, om de opnåede forsøgsresultater kan opfattes som et eksperimentelt bevis for, at i
middel over 80% af den dyreste råvare udnyttes, når C2 benyttes.
3) Forudsat, at man i spørgsmål 2 kan bevise, at i middel over 80% udnyttes. Skal opstilles et
(tosidet) 95% konfidensinterval for E(X).
Vi antager i det følgende, at X (approksimativt) er normalfordelt nxs ( , ) .
4) Beregn sandsynligheden for, at udnyttelsesprocenten X er mindre end 80%, når C 2 benyttes.
66

67
Opgaver til kapitel 6
Opgave 6.4
Et kemikalium fremstilles industrielt ved inddampning af en bestemt opløsning. Det var vigtigt,
at denne opløsning var svagt basisk med pH = 8.0. Man foretog derfor kontrolmæssigt
nogle pH-bestemmelser for den benyttede opløsning. Følgende værdier fandtes:
8.2 8.3 7.9 8.2 7.8 8.6 8.9 7.8 8.2
a) Foretag en testning af om opløsningen kan antages at opfylde kravet til pH-værdi
b) Forudsat, at man i spørgsmål a kan bevise, at opløsningen ikke opfylder kravet, skal opstilles
et 95% konfidensinterval for pH-værdien.
Opgave 6.5
Man frygter, at den såkaldte “ syreregn er årsag til, at en bestemt skov er stærkt medtaget.
Man måler SO 2 - koncentrationen forskellige steder i skovbunden (i g/m 3 ) og finder:
µ
32.7 23.9 21.7 18.6 27.6 35.1 42.2 36.5 13.4 41.8 34.3 30.0
I ubeskadede skove er SO2 - koncentrationen 20 g/m 3 µ .
a) Giver forsøgene et bevis for, at middelkoncentrationen af SO2 i den beskadigede skov er
større end normalt?
b) Forudsat, at man i spørgsmål a kan bevise, at middelkoncentrationen af SO2 i den beskadigede
skov er større end normalt, skal man angive et tosidet 95%-konfidensinterval for SO2 - koncentrationen.
Opgave 6.6
Et nyt måleapparat påstås at give måleresultater med spredningen σ = 1.8 mg/l ved måling af
salt-indholdet i en opløsning. Da dette er mindre end det sædvanlige, køber et laboratorium et
eksemplar af apparatet for at kontrollere påstanden.
Der foretages 15 målinger med følgende resultater:
3.4 7.7 6.0 8.1 8.4 2.7 4.9 1.2 2.1 5.4 3.5 1.5 5.2 4.1 3.9
Test på basis af disse resultater, om spredningen afviger fra 1.8 mg/l.
(Husk altid at anføre: Hvad X er. Antagelser. Nulhypotese. Beregninger. Konklusion.).
Opgave 6.7
En medicinalvarefabrik overvejer at indføre en ny analysemetode.
Det formodes, at spredningen er mindre end 2.0 mg/l.
Man ved, at den nye metode er uden systematiske fejl.
Der fremstilles ved afvejning et præparat med nøjagtig 40.5 mg/l, dvs. middelværdien er kendt.
Følgende måleresultater (i mg/l) findes med den nye metode:
42.8 39.3 41.2 40.9 40.2 40.7 40.6 40.0 41.5
1) Bekræfter de foretagne observationer forhåndsformodningen om spredningen.
(Husk altid at anføre: Hvad X er. Antagelser. Nulhypotese. Beregninger. Konklusion.).
2) Angiv et estimat for spredningen.
3) Angiv et 95% konfidensinterval for spredningen.

Hypotesetestning (1 normalfordelt variabel)
Opgave 6.8
Ved indkøbet af et nyt måleapparat oplystes det, at apparatet målte med en spredning på 2.8
enheder. Efter at have brugt apparatet et stykke tid nærede køberen mistanke om, at apparatet
målte med større spredning end oplyst.
For at få spørgsmålet undersøgt lod køberen en bestemt måling udføre et antal gange.
Følgende resultater fandtes:
18.8 15.5 12.2 14.8 4.80 1.20 1.43 9.60 1.39 1.17 5.60 1.27 1.35
8.70 1.23 1.40 1.02 1.65 1.91 1.14 1.46 1.59 1.54 1.01 1.80
Hvilke konklusioner kan køberen drage ud fra en statistisk analyse af de fundne forsøgsresultater?
Opgave 6.9
En sukkerfabrik leverer sukkeret i 1 kg-poser og 2 kg-poser. Vægten af de fyldte poser varierer.
1) For 1 kg-posernes vedkommende antages vægten at have en middelværdi på 1000 gram.
En række forsøg har vist, at sandsynligheden for, at en tilfældig udtaget 1 kg-pose vejer
mere ned 1025 gram, er 10%. Giv på det grundlag en vurdering af spredningen.
2) For 2 kg-posernes vedkommende bør middelværdien være 200 gram, og spredningen må
ikke overstige 25 gram. For at kontrollere, om en ny pakkemaskine overholder disse normer,
udtages tilfældigt 100 pakker af denne maskines produktion. Gennemsnittet beregnes
til x = 2008 gram, og et estimat for spredningen til s = 25 gram.
Det formodes på forhånd, at den nye maskine overholder de ovennævnte normer. Foretag
en statistisk vurdering af, om dette kan antages at være tilfældet.
Opgave 6.10
Under produktionen forekommer blandt en fabriks affaldsprodukter 1,5 mg/l af et stof A,
som i større mængder kan være kræftfremkaldende. Man håber ved en ny og mere kostbar
metode, at formindske indholdet af det pågældende stof.
1) Inden man lavede forsøgene, foretog man en dimensionering. Hvis formindskelsen er under
0.2 mg/l, er det ikke rimeligt at gå over til den nye metode. Man ønsker derfor at finde
det mindste antal målinger, der skal indgå i undersøgelsen, for at man ved en ændring i
indholdet af A på ∆ = 0.2 mg/l højst har, at P (type II fejl) = β = 10%.
Man har en begrundet formodning om, at spredningen i resultaterne højst kan være 0.21
mg/l ( α = 0.05 ).
2) Ved en række kontrolmålinger efter tilsætning af additivet fandtes følgende resultater (i
mg/l)
1.12 1.47 1.35 1.27 1.17 1.26 1.83 1.10 1.39 1.25 1.44 1.14
Test på 5% niveau, om målingerne beviser, at der er sket en formindskelse af middelindholdet
af stoffet A. (Husk altid at anføre: Hvad X er. Antagelser. Nulhypotese. Beregninger.
Konklusion.).
3) Er det på basis af resultaterne muligt at vurdere, om den fundne formindskelse er stor nok
til, at man vil gå over til den nye metode?
68

69
Opgaver til kapitel 6
Opgave 6.11
På et kraftvarmeværk mener man, at en ny metode vil kunne formindske svovlindholdet i de
slagger, der bliver tilbage efter kulfyringen. Med en bestemt kvalitet kul, har det hidtidige svovlindhold
været 2.70 %.
For at vurdere den nye metode ønsker ingeniøren at foretage en række forsøg.
1) Hvor mange forsøg skal der mindst foretages, hvis α = 5%, β = 10%, ∆ = 0.05 og et over-
slag over spredningens størrelse sætter den til højst 0.08%.
2) Uanset resultatet af dimensioneringen i spørgsmål 1), er der kun praktiske muligheder for at
lave 16 forsøg. Følgende værdier af svovlindholdet fandtes (%).
2.58 2.64 2.80 2.50 2.52 2.69 2.60 2.73 2.61 2.62 2.65 2.58 2.70 2.67 2.62 2.64
Test om disse måleresultater beviser, at svovlindholdet ved den nye metode i middel er blevet
mindre.
3) Er det på basis af resultaterne muligt at vurdere, om den fundne formindskelse er stor nok til,
at man vil gå over til den nye metode?
Opgave 6.12
På pakken af en iscreme står, at portionen indeholder 14 gram fedt. For at kontrollere dette købes
n pakker is, og fedtindholdet måles.
1) Bestem den nødvendige stikprøvestørrelse n, for at man ved en forskel i fedtindhold på ∆
= 0.50 gram højst har, at P (type I fejl) = α = 0.01 og P (type II fejl) = β = 0.05.
( σ ≈ 042 . gram).
2) Man finder et gennemsnit på 13.1 gram og et estimat s for spredningen på 0.42 gram.
Kan man ud fra disse data bevise på signifikansniveau α = 0.01, at middelindholdet afviger
fra 14 gram? (Husk altid at anføre: Hvad X er. Antagelser. Nulhypotese. Beregninger.
Konklusion.).
2) Angiv et estimat for middelindholdet.
3) Forudsat, at man i spørgsmål 1 kan bevise, at middelindholdet afviger fra 14 gram, skal angives
et 95% konfidensinterval for middelindholdet.

7. Hypotesetest 2 variable
7 . HYPOTESETEST
TO NORMALFORDELTE VARIABLE
7.1 INDLEDNING
I dette kapitel benyttes følgende eksempel til at forklare problemstilling, metode osv.
Eksempel 7.1. Sammenligning af 2 normalfordelte variable
To produktionsmetoder M1 og M2 ønskes sammenlignet. Der udvælges tilfældigt 20 personer,
hvoraf de 10 bliver sat til at arbejde med den ene metode, og de 10 andre med den anden.
Efter 2 ugers forløb, beregnede man for hver person det gennemsnitlige tidsforbrug pr. enhed.
Da metode 1 er mere kostbar end metode 2, ønsker man kun at gå over til den, hvis tidsforbruget
pr. enhed ved metode 1 er mindst 2 minutter mindre end ved metode 2.
Man fik følgende resultater.
87.8 91.9 89.8 89.0 92.6 89.4 91.4 88.7 90.1 92.4
M 1
M 2
92.4 94.6 93.0 94.0 92.4 92.9 96.4 92.1 92.8 93.4
For at forsøgsresultaterne skal være “statistisk gyldige”, skal målingerne være uafhængige og
repræsentative for det man skal undersøge.
Det er således ikke korrekt, hvis man i eksempel 7.1 først udtager 10 personer, foretager målingerne,
laver en test, opdager man ikke kan vise at metode 1 giver 2 minutters lavere tidsforbrug,
udtager yderligere 10 personer , tester på de samlede fremkomne tal, osv. indtil man opnår den
ønskede signifikans.
Forsøg bør udføres så der er lige mange gentagelser.
Det er klart, at det ville være forkert, at udtage 2 personer til at arbejde med metode M 1 og 18
personer til at arbejde med metode M 2.
Hvis en af personerne bliver syg under arbejdet, så der kun er 9 på det ene hold, ødelægger det
dog ikke testen.
Ved sammenligning af 2 normalfordelte variable er der afhængigt af hvordan stikprøven er
indsamlet valg mellem 2 metoder.
Er stikprøverne for de to variable som i eksempel 7.1 indsamlet ” uafhængigt af hinanden “
benyttes sædvanligvis den i appendix 7.1 angivne metode.
Er observationerne indsamlet “parvist” skal man benytte den i eksempel 7.3 angivne metode.
70

7.2 Sammenligning af 2 normalfordelte variable
7.2. SAMMENLIGNING AF 2 NORMALFORDELTE VARIABLE
Eksempel 7.1. Sammenligning af 2 normalfordelte variable
To produktionsmetoder M1 og M2 ønskes sammenlignet. Der udvælges tilfældigt 20 personer,
hvoraf de 10 bliver sat til at arbejde med den ene metode, og de 10 andre med den anden.
Efter 2 ugers forløb, beregnede man for hver person det gennemsnitlige tidsforbrug pr. enhed.
Da metode 1 er mere kostbar end metode 2, ønsker man kun at gå over til den, hvis tidsforbruget
pr. enhed ved metode 1 er mindst 2 minutter mindre end ved metode 2.
Man fik følgende resultater.
87.8 91.9 89.8 89.0 92.6 89.4 91.4 88.7 90.1 92.4
M 1
M 2
92.4 94.6 93.0 94.0 92.4 92.9 96.4 92.1 92.8 94.6
1) Undersøg på basis af disse resultater, om det på et signifikansniveau på 5% kan påvises at
tidsforbruget ved metode M1 er 2 minutter mindre end ved metode M2 2) Hvis dette kan påvises, skal der angives et 95% konfidensinterval for differensen i tidsforbrug.
Løsning:
a) Lad X1 = udbyttet ved anvendelse af metode M1 og
X2 = udbyttet ved anvendelse af metode M2. X1 og X2 antages approksimativt normalfordelte med middelværdi og spredning henholdsvis
µ , σ og µ , σ .
1 1 2 2
H0: µ 2 − µ 1 = 2
H: µ 2 − µ 1 > 2
Begrundelse: Nulhypotesen udtrykker jo, at intet er ændret (nul virkning),
så den angiver, at differensen i middeltidsforbruget er præcist 2.
Begrundelse: Den alternative metode udtrykker jo det vi ønsker at bevise,
så den angiver, at differensen i middeltidsforbruget er større end 2.
Såvel TI89 som Excel anvender et færdigt program, der anvender en testmetode (Satterthwaites metode), som
er robust overfor mindre afvigelser fra kravet om normalitet, når blot antallet af gentagelser er (næsten) den
samme.
Er det ikke tilfældet kan man stadig foretage testen, men så stilles der større krav til, at de variable X 1 og X 2
virkelig er normalfordelte.
Formlen for Satterthwaites metode kan findes i oversigt 7.
TI89: Hypoteserne omskrives til
: µ + 2 = µ H: µ + 2 < µ
H 0 1 2
1 2
APPS, STAT/LIST , indtast data i list1 og list 2 F6, 4: 2 - SampTtest ENTER
I den fremkomne menu vælg Data ok
71
µ < µ
I menu for “list 1" skrives list1+2, for “alternative Hyp”
Man får P-værdi = 0.0464.
Excel: Tallene for metode 1 indtastes i A1 til A10
Tallene for metode 2 indtastes i B1 til B10
1 2 og pooled til “NO” OK
I C1 til C10 indsættes tallene fra A-kolonnen +2 (Skriv i C1 =A1+2 , og kopiere resultat ned)
På værktøjslinien foroven: Tryk på f x Vælg kategorien “Statistisk” Vælg “TTEST”
Tabel udfyldes: =TTEST(C1:C10;B1:B10;1;3)
P-værdi= 0,0464
Da P-værdi =4.64% < 5% forkastes H 0, dvs. vi har bevist, at tidsforbruget ved metode M 1 er 2
minutter mindre end ved metode M 2.

7. Hypotesetest 2 variable
2) 95% Konfidensinterval for differens
TI89: F7, 4: 2 - SampTint ENTER I den fremkomne menu vælg Data ok
I menu for “list 1" skrives blot list2, osv. poole til “No” OK
Differensen er 3.21 og 95% konfidensinterval for differensen er [1.77 ; 4.64]
Excel:
Excel har intet program til beregning af konfidensinterval, så man må benytte formlen
µ 1 − µ 2:
x1− x2− t0975 , ( f ) ⋅ c ≤ µ 1− µ 2 ≤ x1− x2+ t0975 , ( f ) ⋅
2
s1
c , hvor c = +
n
2
s2
n
c
og frihedsgradstallet f er det nærmeste hele tal der er større end g =
⎛ s ⎞ s
⎜ ⎟
⎝ n ⎠ n
n − n
+
2
2
2
2
2
⎛ ⎞
1
2
⎜ ⎟
1 ⎝ 2 ⎠
1 −1
xA streg= MIDDEL(A1:A10) 90,31
xB streg= MIDDEL(B1:B10) 93,52
vA= VARIANS(A1:A10) 2,785444
VB= VARIANS(B1:B10) 1,839556
n1= 10
n2= 10
c= G3/G5+G4/G6 0,4625
f= AFRUND.LOFT(G7^2/((G3/G5)^2/(G5-1)+(G4/G6)^2/(G6-1));1) 18
Differens G2-G1 3,21
Nedre grænse G2-G1-TINV(0,05;G8)*KVROD(G3/G5+G4/G6) 1,781219
Øvre grænse G2-G1+TINV(0,05;G8)*KVROD(G3/G5+G4/G6) 4,638781
Differensen er 3.21 og 95% konfidensinterval for differensen er [1.77 ; 4.64]
Gemmes ovenstående excelfil, kan man nu hurtigt finde konfidensinterval for andre data.
Eksempel 7.2. Sammenligning af 2 normalfordelte variable (oprindelige data ikke givet)
Et luftfartsselskab A hævder, at dets fly til USA i gennemsnit afgår mere præcist end et konkurrerende
luftfartsselskab.
En forbrugergruppe undersøger denne påstand ved i en given periode at bestemme forsinkelserne
for samtlige flyafgange til USA for hver af de to selskaber.
Man fandt følgende tal:
Luftfartsselskab Antal afgange x s
A 100 55 minutter 30 minutter
B 80 60 minutter 35 minutter
Støtter undersøgelsen luftfartsselskab A's påstand?
72
1
2
1
2

7.2 Sammenligning af 2 normalfordelte variable
Løsning:
XA = forsinkelsen i minutter for luftfartselskab A.
XB =forsinkelsen i minutter for luftfartselskab B.
XA og XB antages approksimativt normalfordelte med middelværdi og spredning henholdsvis µ A, σ A
og µ B, σ B .
Da vi ønsker at vise, at A er mere præcise end B, så haves:
H : µ = µ H:
µ < µ
0
A B A B
TI89 Da antal forsøg er over 30 kunne man strengt taget nøjes med at lave en Z - test, i stedet
for den normale t - test.
t - test: APPS STAT/LIST F6, 4 2 - SampTtest ENTER
I den fremkomne menu vælg STATS OK (da forsøgsresultaterne resultater ikke er kendt)
µ < µ
Menuen udfyldes bl.a. “alternative Hyp” 1 2 og poole til “N” OK
P-værdi = 0.156
Konklusion: Da P-værdi > 0.05 accepteres H 0 , dvs.
vi kan ikke vise, at A er mere præcis end B.
Excel har intet program til beregning af P-værdi, så man må benytte formlen fra oversigt 7
x1 −x2 −d
t =
c
2
s1
, hvor c = +
n
2
s2
P-værdi = P(T < t)
n
1
2
c
=
⎛ s ⎞ s
⎜ ⎟
⎝ n ⎠ n
n − n
+
2
2
2
2
2 ⎛ ⎞
1
2
⎜ ⎟
1 ⎝ 2 ⎠
1 1 2 −1
A B C D E
1
2
Eksempel 7.2
3 XA =forsinkelsen for luftfartselskab A XA er normalfordelt med middelværdi :A
4 XB =forsinkelsen for luftfartselskab A XB er normalfordelt med middelværdi :B
5 H0: :A =B H: A < B
6 Data Beregning
7 nA = 100 a= B9^2/B7 9
8 x-streg-A= 55 b= B12^2/B10 15,3125
9 sA = 30 c= E7+E8 24,3125
10 nB = 80 t= (B8-B11-B13)/KVROD(E9) -1,01404
11 x-streg-B= 60 g= E9^2/(E7^2/(B7-1)+E8^2/(B10-1)) 156,1194
12 sB = 35 f = RUND.OP(E11;0) 157
13 d= 0 P-værdi= TFORDELING(ABS(E10);E12;1) 0,156062
14 Konklusion: Da p -værdi > 0.05 accepteres H0, dvs.
15 det kan ikke på dette grundlag vises, at A er mere præcis end B
og frihedsgradstallet f er det nærmeste hele tal der er større end g
73

7. Hypotesetest 2 variable
Parvise observationer
Parvise observationer (Matched pairs samples) kan anvendes, hvis det har mening at sammen
ligne observationerne to og to (i par)
Som et eksempel herpå vil vi igen betragte problemstillingen i eksempel 7.1, men nu antage, at
forsøget er foretaget på en anden måde.
Eksempel 7.3. Parvise observationer
To produktionsmetoder M1 og M2 ønskes sammenlignet. Der udvælges tilfældigt 10 personer.
Efter lodtrækning bliver 5 personer sat til først i 2 uger, at arbejde med produktionsmetode M1
og derefter i de næste 2 uger med produktionsmetode M2.
De øvrige 5 personer arbejder omvendt først med metode M2 og derefter med metode M1.
Efter 2 ugers forløb, beregnede man for hver person det gennemsnitlige tidsforbrug pr. enhed.
Da metode 1 er mere kostbar end metode 2, ønsker man kun at gå over til den, hvis tidsforbruget
pr. enhed ved metode 1 er mindst 2 minutter mindre end ved metode 2.
Man fik følgende resultater.
Person nr. 1 2 3 4 5 6 7 8 9 10
M 1 87.8 91.9 89.8 89.0 92.6 89.4 91.4 88.7 90.1 92.4
M 2 92.4 94.6 93.0 94.0 92.4 92.9 96.4 92.1 92.8 93.4
1) Undersøg på basis af disse resultater, om det på et signifikansniveau på 5% kan påvises at
tidsforbruget ved metode M 1 er 2 minutter mindre end ved metode M 2
2) Angiv endvidere et 95% konfidensinterval for differensen mellem de to middeludbytter.
Forklaring på metode:
Da en forsøgsperson kan være hurtig og en anden langsom (person 1 er således hurtigere end
person 2) kan spredningen på M 1 og M 2 være så stor, at man intet kan vise.
Hvis man i stedet tager differenserne M2 - M1 vil disse forskelle jo udjævnes, da person 1 jo er
hurtig under arbejdet med begge metoder, mens person 2 er langsom ved begge.
Person nr. 1 2 3 4 5 6 7 8 9 10
M 1 87.8 91.9 89.8 89.0 92.6 89.4 91.4 88.7 90,1 92,4
M 2 92.4 94.6 93.0 94.0 92.4 92.9 96.4 92.1 92,8 94,6
D = M 2 - M 1 4.6 2.7 3.2 5 -0.2 3.5 5 3.4 2,7 2,2
I stedet for at benytte metoden i eksempel 7.1 kan vi nu teste nulhypotesen
H : D=
2 mod H: D > 2 ved metoden i eksempel 6.2 (en variabel)
0
Løsning:
1) D = forskellen i tidsforbruget ved metode M2 og metode M1 D antages approksimativt normalfordelt med middelværdi µ og spredning σ .
H 0: D = 2 H: D > 2
TI89:Data indtastes (de samme som i eksempel 6.1)
APPS STAT/LIST data indtastes i list 1 og list 2 Cursor på list 3 list2 - list 1
Enter F6 t-test menu udfyldes
P-værdi = 0.0178
74

7.2 Sammenligning af 2 normalfordelte variable
Excel
Tallene for metode 1 indtastes i A1 til A10
Tallene for metode 2 indtastes i B1 til B10
I C1 til C10 indsættes tallene fra A-kolonnen +2 (Skriv i C1 =A1+2 , og kopiere resultat ned)
På værktøjslinien foroven: Tryk på f x Vælg kategorien “Statistisk” Vælg “TTEST”
Tabel udfyldes: =TTEST(C1:C10;B1:B10;1;1)
P-værdi= 0,017836
Konklusion: Da P-værdi < 0.05 forkastes H 0, dvs.
M1 er signifikant 2 minutter lavere end M2, dvs. man vil gå over til at benytte metode M1
2) Konfidensinterval for differens:
TI89:F6 t-interval menu udfyldes
Differens = 2.31 KONFIDENSINTERVAL [2.10 ; 4.32 ]
Excel: Danner en kolonne D1 til D10 med differenserne mellem A og B kolonner.
På værktøjslinien foroven: Tryk på f x Vælg kategorien “Statistisk” Middel
Excel: 2003: Funktioner 2007: Data
derefter Dataanalyse Beskrivende statistik udfyld inputområde vælg konfidensniveau
Resultat
x streg 3,21
Konfidensniveau(95,0%) 1,10896985
nedre grænse 2,1011
øvre grænse 4,3190
75

7. Hypotesetest 2 variable
7.3 OVERSIGT over centrale formler i kapitel 7
Test af middelværdier µ og µ og konfidensinterval for differens µ − µ for 2 normalfordelte
1 2
1 2
variable .
X1 og X2 antages normalfordelte henholdsvis n( µ 1, σ1)
og n( µ 2, σ2)
.
Givet 2 stikprøver af X1 og X2. Størrelse, gennemsnit og spredning henholdsvis n1, x1 , s1 og n2, x2 , s2. Signifikansniveau er Lad d være en given konstant.
α
Forudsætninger Alternativ
hypotese H
σ , σ ukendte
1 2
x1 − x2 − d
t =
c
f er det nærmeste
hele tal, som
er større end g
Forudsætninger
s
n
2
1
s
n
2
2
Forkortelser: a =
1
, b =
2
c
, c = a + b, g =
a b
n − n
+
2
2
2
1 1 2 −1
T er t - fordelt med frihedsgradstallet f.
P - værdi Beregning H 0 forkastes
µ 1 > µ 2 +d PT ( ≥ t)
TI89: tCdf (, t ∞,
f ) eller
F6: 2-sampTtest,pooled, No
Excel:TTEST(se eksempel 7.1)
µ 1 < µ 2 +d PT ( t)
≤ TI89: tCdf ( −∞,
t, f ) eller
µ 1 ≠ µ 2 +d PT ( ≥ t)
for x1 > x2 + d
PT ( ≤ t)
for x < x + d
1 2
76
F6: 2-sampTtest,pooled, No
Excel:TTEST(se eksempel 7.1)
som række 1
som række 2
100⋅ ( 1−
α )% konfidensinterval for differens µ 1 − µ 2 :
x − x − t ( f ) ⋅ c ≤ µ − µ ≤ x − x + t ( f ) ⋅ c
1 2
α 1 2 1 2 α
1− 1− 2
2
TI89: F7, 2-SampTint Excel: Formel benyttes: se eksempel 7.1
2 2
σ1σ2 Forkortelser: x = x1 −x2 −d
σ = + Y er normalfordelt
n n
Alternativ
hypotese H
1
2
P - værdi x2 + d
PY ( ≤ x)
for x < x + d
1 2
normCdf ( −∞ , x,
µ , σ )
eller F6: 2-sampZtest
Excel: ZTEST
som række 1
som række 2
100⋅( 1−α
)% konfidensinterval for differens µ 1 − µ 2 :
x −x −u ⋅σ ≤ µ −µ ≤ x − x + u ⋅σ
1 2
α 1 2 1 2 α
1− 1− 2
2
TI89: F7, 2-SampZint Excel: Formel benyttes:
P - værdi

OPGAVER
77
Opgaver til kapitel 7
Opgave 7.1
Det påstås at modstanden i en tråd af type A er større end modstanden i en tråd af type B. Til afklaring af denne
påstand udtages tilfældigt 6 tråde af hver type og deres modstande måles.
Følgende resultater fandtes:
Modstand i tråd A (i ohm) 0.140 0.138 0.143 0.142 0.144 0.137
Modstand i tråd B (i ohm) 0.135 0.140 0.142 0.136 0.138 0.140
Hvilke konklusioner kan drages med hensyn til påstanden?
Opgave 7.2
Et levnedsmiddelfirma havde udviklet en diæt, som har lavt indhold af fedt, kulhydrater og kolesterol. Diæten er
udviklet med henblik på patienter med hjerteproblemer, men firmaet ønsker nu at undersøge diætens virkning på folk
med vægtproblemer.
To stikprøver på hver 100 personer med vægtproblemer blev udtaget tilfældigt. Gruppe A fik den nye diæt, mens
gruppe B fik den diæt, man normalt gav. For hver person blev registreret størrelsen af vægttabet i en 3 ugers periode.
Man fandt følgende værdier for gennemsnit og spredning:
Gruppe A: x A = 931 . kg , sA = 467 .
Gruppe B: xB = 740 . kg , sB = 404 . .
α = 5%
1) Undersøg om vægttabet for gruppe A er signifikant større end for gruppe B. Signifikansniveau .
2) I tilfælde af signifikans beregn da et 95% konfidensinterval for differensen mellem de to gruppers middelværdier.
Opgave 7.3
I et laboratorium foretoges 15 uafhængige bestemmelser af furfurols kogepunkt, idet 8 af bestemmelserne foretoges
af én kemiingeniør, de resterende bestemmelser af en anden kemiingeniør. Resultaterne var ( 0 C ) :
1. ingeniør 162.2 161.3 161.9 161.2 163.4 162.4 162.5 162.0
2. ingeniør 163.3 162.6 161.8 163.8 163.0 163.2 164.1
Undersøg, om de to ingeniørers resultater i middel er ens.
Opgave 7.4
På et laboratorium undersøgtes filtreringstiden for en opløsning af et bestemt gødningsstof ved benyttelsen af to
forskellige filtertyper (F1) og (F2). Følgende stikprøveværdier observeredes:
(F1) 8 10 12 13 13 9 14 10
(F2) 9 10 10 7 9 11 7
Det antages, at filtreringstiderne X1 og X2 er normalfordelte n( µ , σ ) og
Test om det kan antages, at filtreringstiderne i middel er forskellige.
1 1 n( µ , σ )
Opgave 7.5
En produktion af plastikvarer må omlægges på grund af bestemmelser i en ny miljølov.
Ved den fremtidige produktion kan inden for miljølovens rammer vælges mellem 2 pro- duktionsmetoder I og II.
Metode I er den dyreste, og fabrikanten har regnet ud, at det (kun) kan betale sig at benytte metode I, såfremt den
giver et middeludbytte, som er mindst 10 måleenheder (udbytteprocenter) større end udbyttet ved benyttelse af metode
II.
Ved et fuldstændigt randomiseret forsøg fandtes følgende måleresultater:
Metode I 35.2 38.1 37.6 37.6 34.9 37.9 36.5 40.0 36.2 37.4 37.2 37.9
Metode II 26.2 22.2 24.3 24.5 22.0 27.6 23.8 22.8 23.4 20.8
Fabrikanten valgte herefter at benytte metode I.
a) Foretag en undersøgelse af, om valget var statistisk velmotiveret.
b) Hvis forslaget er velmotiveret skal der opstilles et 95% - konfidensinterval for differensen mellem middeludbytterne
ved benyttelse af metoderne l og II.
2 2

7. Hypotesetest 2 variable
Opgave 7.6
To sjællandske fabrikker producerer begge en bestemt type kvægfoder, for hvilken det ønskes, at proteinindholdet i
færdigvaren skal være 26%. På de 2 fabrikkers driftslaboratorier foretoges følgende målinger af proteinindholdet i en
uges produktion:
Fabrik 1 27.3 26.1 26.9 24.8 26.2 25.7 26.5
Fabrik 2 26.0 26.7 25.6 26.1 26.2 25.5 26.0 26.1 26.2 25.9
Foretag en statistisk vurdering af, om de to produktioner kan antages i middel at give kvægfoder med samme proteinindhold.
Opgave 7.7
Måling af intelligenskvotient på 16 tilfældigt udvalgte studerende ved en diplom-retning (med mere end 200 stu-
2
derende) viste et gennemsnit på = 107 og en empirisk varians på =100, medens en tilsvarende måling på 14
x1 s1 tilfældigt udvalgte studerende fra en anden diplomretning viste et gennemsnit på x2 =112 og en empirisk varians på
2
s2 = 64.
Tyder disse tal på en forskel på studentermaterialet på de to retninger?
Opgave 7.8
Et bestemt medikament ønskes testet for dets effekt på blodtrykket. 12 mænd fik deres blodtryk målt før og efter
indtagelse af medikamentet. Resultaterne var:
mand nr 1 2 3 4 5 6 7 8 9 10 11 12
Før 120 124 130 118 140 128 140 135 126 130 126 127
Efter 128 131 131 127 132 125 141 137 118 132 129 135
Udfør en testning af, om disse tal tyder på, at medikamentet påvirker blodtrykket.
Opgave 7.9
Et diætprodukt påstår i en reklame, at brug af produktet i en måned vil resultere i et vægttab på 3 kg.
En forbrugerorganisation ønsker at teste denne påstand, dvs. om vægttabet er netop 3 kg
8 personer bruger produktet i en måned, og resultatet fremgår af nedenstående tabel:
Person nr 1 2 3 4 5 6 7 8
Startvægt 81 101 98 99 78 71 75 93
Slutvægt 79 95 95 97 73 69 71 89
1) Undersøg på grundlag af disse tal, om det på basis af disse tal på et signifikansniveau på 5% kan vises, at reklamens
påstand er fejlagtig, dvs. om vægttabet afviger signifikant fra 3 kg?
2) Opstil et 95% tosidet konfidensinterval for middelværdien af vægttabet, og giv på grundlag heraf en vurdering af
virkningen af diætproduktet.
78

79
Opgaver til kapitel 7
Opgave 7.10 (parvise observationer).
En producent af malervarer har laboratorieresultater, der tyder på, at en ny lak A, har en større slidstyrke end den
sædvanlige lak B. Han ønsker en afprøvning i praksis og aftaler med ejerne af 6 bygninger med mange trapper, at han
må lakere deres trapper. Efter 3 måneders forløb måles graden af slid (i %) i hver bygning.
1) Angiv hvorledes du ville foretage forsøget.
2) De målte værdier af slid efter valg af plan var
Bygning nr 1 2 3 4 5 6
Ny lak 20.3 25.1 21.8 19.6 18.9 23.5
Sædvanlig lak 19.5 28.4 21.6 22.0 20.9 25.8
Undersøg om observationerne leverer et eksperimentelt bevis for, at den nye lak er mere slidstærk end den sædvanlige
lak.

8. Regneregler for sandsynlighed, Kombinatorik
8. REGNEREGLER FOR SANDSYNLIGHED,
KOMBINATORIK
8.1 REGNEREGLER FOR SANDSYNLIGHEDER
Vi har tidligere omtalt sandsynlighed.
I dette kapitel omtales nogle af de grundlæggende definitioner og begreber
Det følgende eksempel blive benyttet til illustration af definitioner og begreber.
Eksempel 8.1. Gennemgående eksempel.
To skytter Anders og Brian skyder hver ét skud mod en skydeskive. Sandsynligheden for at
Anders rammer skiven er 0.80 mens Brian har en træfsandsynlighed på 0,60.
Et eksperiment består i at de hver skyder et skud.
Lad A være hændelsen at Anders rammer skiven og lad B være sandsynligheden for at Brian
rammer skiven.
Vi har derfor, at P(A) = 0.80 og P(B) = 0.60.
Lad os ved at sætte en streg over A forstå “ikke A”.
Generelt gælder P( A)
= 1 - P ( A )
I eksempel 8.1 er A hændelsen at Anders ikke rammer skiven.
Vi har derfor, at P( A ) = 1 - P(A) = 1 - 0.8 = 0.20
Fællesmængden til A og B benævnes A ∩ B og er
mængden af alle udfald i udfaldsrummet U, der tilhører
både A og B (Den skraverede mængde i figur 8.1 ).
Eksempelvis er A ∩ B i eksempel 8.1 hændelsen, at
både Anders og Brian rammer skiven
Foreningsmængden af A og B benævnes A∪B og
er mængden af alle udfald i udfaldsrummet U, der
enten tilhører A eller B eventuelt dem begge (den
skraverede mængde på figur 8.2 )
Eksempelvis er A∪B i eksempel 6.1 den hændelse,
at enten rammer Anders eller også rammer Brian
skiven eventuelt gør de det begge.
Man kunne også udtrykke det ved at mindst en af dem
rammer skiven.
80
Fig 8.1. Fællesmængde
Fig. 8.2 Foreningsmængde

Der gælder nu følgende sætninger:
Additionssætning: P( A∪ B) = P( A) + P( B) − P( A∩B). Sætningen fremgår umiddelbart ved at betragte arealerne i figur 8.3.
P( AUB) PA ( )
81
6.2 Regneregler for sandsynligheder
Statistisk uafhængighed.
To hændelser A og B siges at være statistisk uafhængige, såfremt sandsynligheden for, at den
ene hændelse indtræffer, ikke afhænger af, om den anden hændelse indtræffer.
I eksempel 8.1 må man eksempelvis antage, at om Anders rammer skiven har ingen indflydelse
på om Brian rammer, så her må man antage A og B er uafhængige.
Et andet eksempel er kast med en terning. Her vil sandsynligheden for at få en sekser i andet kast
være uafhængigt af udfaldet i første kast
Der gælder følgende sætning:
Produktsætning for uafhængige hændelser:
Eksempel 8.2 (eksempel 8.1 fortsat)
Lad A være hændelsen, at Anders rammer skiven, og lad B være hændelsen, at Brian rammer
skiven. Det er givet, at P(A) = 0.80 og P(B) = 0.60.
Find sandsynligheden for
a) At både Anders og Brian rammer skiven
b) At enten Anders eller Brian (evt. begge) rammer skiven, dvs. mindst en af dem rammer
skiven.
c) At hverken Anders elle Brian rammer skiven
Løsning:
a) Da hændelserne antages at være uafhængige gælder ifølge produktsætningen
P( A∩ B)
= 08 . ⋅ 06 . = 048 .
PB
Fig.8.3 Additionssætning
For to uafhængige hændelser gælder P( A∩ B) = P( A) ⋅
P( B)
( ) PA ( I B)
b) Ifølge additionssætningen gælder P( A∪ B)
= 06 . + 08 . − 048 . = 092 .

8. Regneregler for sandsynlighed, Kombinatorik
c) P( A∩ B) = P( A) ⋅ P( B)
= ( 1−08 . )( 1− 06 . ) = 008 .
Produktsætning og additionssætning kan generaliseres til flere hændelser end 2.
For tre hændelser A, B og C gælder således
P( A∪B∪ C) = P( A) + P( B) + P( C) − P( A∩B) − P( A∩C) − P( B∩C) I tilfælde af at hændelserne A, B og C er uafhængige gælder således:
P( A∩B∩ C) = P( A) ⋅P( B) ⋅P(
C)
.
Er hændelserne A og B ikke uafhængige, kan man som beskrevet i afsnit 11.3 udlede en mere
generel produktsætning
8.2. Betinget sandsynlighed
Er hændelserne A og B ikke uafhængige vil PA ( ∩ B) ≠ PA ( ) ⋅ PB ( )
Eksempel 8.3. Ikke uafhængige hændelser
En fabrik har erfaring for, at den daglige produktion af glasfigurer indeholder 10 % misfarvede, 20% har ridser, og
1 % af produktionen er både ridsede og misfarvede.
Et eksperiment består i tilfældigt at udtage en glasfigur af produktionen. Lad A være hændelsen at få en misfarvet
og lad B være hændelsen at få en ridset.
Her er P( A) ⋅ P( B) = 01 . ⋅ 02 . = 002 . ≠ P( A∩ B)
= 001 . .
For at få en mere generel regel indføres PBA ( ) som kaldes sandsynligheden for, at B indtræffer, når A er indtruffet
(den af A betingede sandsynlighed for B).
For at forklare den følgende definition, vil vi simplificere eksempel
8.3, idet vi antager, at den daglige produktion er 100 glasfigurer.
I så fald er der 10 misfarvede figurer, 20 ridsede figurer, og
1 figur der er både misfarvet og ridset.
Hvis vi begrænser vort udfaldsrum til A, så er
1
1 P( A B)
PBA ( ) = =
100 ∩
= .
10 10 P( A)
100
Denne beregning begrunder rimeligheden i følgende definition:
82
Fig. 8.4 Taleksempel
Den af A betingede sandsynlighed for B PBA ( ) (eller sandsynligheden for, at B indtræffer, når A er indtruffet )
PA ( ∩ B)
defineres ved PBA ( ) = .
P( A)
Ved multiplikation fås Produktsætningen: P( A∩ B) = P( A) ⋅P(
B A)
.
Benyttes produktsætningen på eksempel 8.1 fås P( A∩ B) = P( A) ⋅ P( B A)
= 01 . ⋅ 01 . = 001
. .

83
8.2 Betinget sandsynlighed
Eksempel 8.4: Betinget sandsynlighed.
En beholder indeholder 3 røde og 3 hvide kugler. Vi udtrækker successivt 2 kugler fra urnen.
Vi betragter følgende 2 hændelser:
A: Den først udtrukne kugle er rød. B: Den anden udtrukne kugle er rød.
Beregn P( A∩B) hvis
1) kugleudtrækningen foregår, ved at den først udtrukne kugle lægges tilbage før den anden udtrækkes.
2) kugleudtrækningen foregår, ved at den først udtrukne kugle ikke lægges tilbage før den anden udtrækkes.
Løsning
1) Her er PBA ( )= og derfor ifølge produktsætningen
3
P( A∩ B) = P( A) ⋅ P( B A)
=
6
1
4
2) Her er PBA ( )= og derfor
2
3 2 1
5 P( A∩ B)
= ⋅ = 6 5 5
Bayes sætning
For to hændelser A og B for hvilken P(A) > 0 gælder
Bevis:
P( A∩B) PB ( ∩ A)
PB ( ) ⋅ PAB ( )
Af definitionen på betinget sandsynlighed og produktsætningen fås PBA ( ) = = =
P( A)
P( A)
P( A)
Bayes sætning gør, at det er let at omskrive fra den ene betingende sandsynlighed til den anden.
Dette er tilfældet, hvis den ene af de to betingede sandsynligheder PBA ( ) og PAB ( ) er meget lettere at
beregne end den anden.
PB ( ) ⋅
PAB ( )
Bayes sætning: PBA ( ) =
P( A)
Eksempel 8.5 (Bayes sætning)
I en officeruddannelse kan man vælge mellem en “teknisk” linie og en “operativ”linie. På en bestemt årgang har 60
% valgt den operative linie og af disse er 20% kvinder. På den tekniske linie er 10% kvinder.
Ved lodtrækning vælges en elev.
a) Find sandsynligheden for, at denne er en kvinde.
Ved ovenstående lodtrækning viste det sig at eleven var en kvinde.
b) Hvad er sandsynligheden for, at hun kommer fra den tekniske linie.
Løsning:
Vi definerer følgende hændelser:
T: Den udtrukne er tekniker
K: Den udtrukne er en kvinde.
a) PK ( ) = PT ( ∩ K) + PO ( ∩ K) = PKT ( ) ⋅ PT ( ) + PKO ( ) ⋅ PO ( ) = 01 . ⋅ 04 . + 02 . ⋅ 06 . = 016 . = 16%
PKT ( ) ⋅ PT ( ) 01 . ⋅04
. 1
b) Af Bayes sætning fås: PTK ( ) =
= = = 25%
PK ( ) 016 . 4
En anden metode ville det være, at antage, at der bliver optaget 100 elever.
Vi har så følgende skema
Kvinder I alt
Operativ 12 60
Teknisk 4 40
16
4
Heraf fås umiddelbart PK ( ) = = 16% og PTK ( ) = = 25%
100
16

8. Regneregler for sandsynlighed, Kombinatorik
8.3. Kombinatorik
8.3.1. Indledning:
Såfremt et udfaldsrum U indeholder n udfald som alle er lige sandsynlige, vil sandsynligheden
for hvert udfald være ( ) = . 1
Pu n
En hændelse A som indeholder a udfald vil da have sandsynligheden a P( A) = .
n
Dette udtrykkes ofte kort ved at sige, at sandsynligheden for A er antal gunstige udfald i A
divideret med det totale antal udfald i udfaldsrummet.
I sådanne tilfælde, bliver problemet derfor, hvorledes man let kan optælle antal udfald. Dette kan
ofte gøres ved benyttelse af kombinatorik.
8.3.2. Multiplikationsprincippet
Multiplikationsprincippet: Lad et valg bestå af n delvalg, hvoraf det første valg
har valgmuligheder, det næste valg har valgmuligheder, . . . og det n’te valg har
r n
r 1
valgmuligheder.
Det samlede antal valgmuligheder er da r1⋅r2⋅.... ⋅rn
Multiplikationsprincippet illustreres ved følgende eksempel.
Eksempel 8.6. Multiplikationsprincippet
En mand ejer 2 forskellige jakker, 3 slips og 4 forskellige fabrikater skjorter.
På hvor mange forskellige måder kan han sammensætte sin påklædning af jakke, slips og skjorte.
Løsning:
1) Valg af jakke giver 2 valgmuligheder
2) Valg af slips giver 3 valgmuligheder
3) Valg af skjorte giver 4 valgmuligheder
Ifølge multiplikationsprincippet giver det i alt 234 ⋅ ⋅ = 24muligheder
Man kunne illustrere løsningen ved følgende “forgreningsgraf”
r 2
84

Eksempel 8.7 Fakultet
På hvor mange måder kan 5 personer opstilles i en kø (i rækkefølge)
Løsning:
Pladserne i køen nummereres 1,2,3,4,5.
Plads nr. 1 i køen besættes 5 valgmuligheder
Plads nr. 2 i køen besættes 4 valgmuligheder
Plads nr. 3 i køen besættes 3 valgmuligheder
Plads nr. 4 i køen besættes 2 valgmuligheder
Plads nr. 5 i køen besættes 1 valgmulighed
I alt 5⋅4⋅3⋅2⋅ 1 = 120 forskellige rækkefølger.
Ved n fakultet (n udråbstegn) forstås n! = n⋅( n−1) ⋅ ( n−2)
⋅ ... ⋅ 2⋅1 Endvidere defineres 0! = 1.
TI89: 5 MATH Probability ! 5! = 120
Excel: f x Math/trig FAKULTET(5) 120
85
8.4 Kombinatorik
8.3.3 Ordnet stikprøveudtagelse
Lad os tænke os vi har en beholder indeholdende 9 kugler med numrene 1, 2, 3, ..., 9 .
Vi udtager nu en stikprøve på 4 kugler. Det kan ske
1) uden tilbagelægning: En kugle er taget op, nummeret noteres, men den lægges ikke tilbage inden man tager en
ny kugle op.
2) med tilbagelægning: En kugle tages op, nummeret noteres, og derefter lægges kuglen tilbage inden man tager en
ny kugle op. Man kan følgelig få den samme kugle op flere gange.
Ved en ordnet stikprøveudtagelse lægges vægt på den rækkefølge hvori kuglerne udtages, .
dvs. der er forskel på 2,1,3,5 og 3,1,2,5
a) Uden tilbagelægning
Eksempel 8.8. Ordnet uden tilbagelægning
I en forening skal der blandt 10 kandidater vælges en bestyrelse
På hvor mange forskellige måder kan man sammensætte denne bestyrelse, hvis
1) Bestyrelsen består af en formand og en kasserer
2 Bestyrelsen består af en formand, en næstformand, en kasserer og en sekretær.
Løsning:
1) En formand vælges blandt 10 kandidater 10 valgmuligheder
En Kasserer vælges blandt de resterende 9 kandidater 9 valgmuligheder
Da der for hvert valg af formand er 9 muligheder for kasserer, følger af multiplikationsprincippet, at det totale
antal forskellige bestyrelser er 10⋅ 9 = 90 .
2) Analogt fås ifølge multiplikationsprincippet at antal forskellige bestyrelser er 10987 ⋅ ⋅ ⋅ = 5040
TI89: MATH Probability nPr(10,4) . Resultat: = 5040
Excel: f x Statistisk PERMUT(10;4) 5040
Eksempel 8.8 begrunder følgende definition
Permutationer. Antal måder (rækkefølger eller “permutationer”) som m elementer kan udtages (ordnet og
uden tilbagelægning) ud af n elementer er Pnm ( , ) = n⋅( n−1) ⋅( n−2)...( ⋅ ⋅ n− m+
1)

8. Regneregler for sandsynlighed, Kombinatorik
b) Med tilbagelægning
Eksempel 8.9. Ordnet, med tilbagelægning
I en forening skal 4 tillidshverv fordeles mellem 10 personer. En person kan godt have flere tillidshverv. På
hvor mange forskellige måder kan disse hverv fordeles.?
Løsning:
Tillidshverv 1 placeres. 10 valgmuligheder
Tillidshverv 2 placeres 10 valgmuligheder
Tillidshverv 3 placeres 10 valgmuligheder
Tillidshverv 4 placeres 10 valgmuligheder
I alt (ifølge multiplikationsprincippet) 10 10 10 10 10 4
⋅ ⋅ ⋅ =
8.3.4. Uordnet stikprøveudtagelse
Eksempel 8.10 Uordnet uden tilbagelægning
En beholder indeholdende 5 kugler med numrene k1, k2, k3, k4, k5
Vi udtager nu en stikprøve på 3 kugler uden tilbagelægning. Rækkefølgen kuglen tages op er
uden betydning, dvs. der er ikke forskel på eksempelvis k1, k4, k2og
k4, k1, k2
Hvor mange forskellige stikprøver kan forekomme?
Løsning:
Antallet er ikke flere end man kan foretage en simpel optælling:
k , k , k , k , k , k k , k , k k , k , k k , k , k k , k , k k , k , k k , k , k k3, k , k
{ } { }{ }{ }{ }{ }{ }{ }{ }
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 2 3 4 2 3 5 2 4 5 4 5
Antal stikprøver = 10
Det er klart, at ren optælling er uoverkommeligt, hvis mængden er stor.
Definition af kombination
Lad M være en mængde med n elementer.
En kombination af r elementer fra M er et udvalg af r elementer udtaget af M uden at tage
hensyn til rækkefølgen af elementer
⎛n
Antallet af kombinationer med r elementer betegnes K(n,r) eller ⎜ (n over r).
⎝r
⎞
⎟
⎠
Sætning 8.1 (Antal kombinationer).
Antal kombinationer med r elementer fra en mængde på n elementer er Knr
86
n!
( , ) =
r!( ⋅ n−r)! Bevis: Beviset knyttes for enkelheds skyld til et taleksempel, som let kan generaliseres.
Lad os antage, vi på tilfældig måde udtager 3 kugler af en kasse, der indeholder 5 kugler med numrene
k1, k2, k3, k4, k5.
5!
Vi skal nu vise, at k( 53 ,) =
3! ⋅2!
Lad os først gå ud fra, at rækkefølgen hvori kuglerne trækkes er af betydning, Der er altså eksempelvis forskel på k1, k3, k4
og k , k , k . Dette kan gøres på P(5,3) = 5⋅4⋅3 måder.
3 1 4

87
8.4 Kombinatorik
Hvis de 3 kugler udtages, så rækkefølgen ikke spiller en rolle, har vi vedtaget, det kan gøres på K(5,3) måder. Lad
en af disse måder være k1, k3, k4.
Disse 3 elementer kan ordnes i rækkefølge på 3! = 3⋅2⋅1måder. P(,)
53
543 54321 5!
Vi har følgelig, at P(,) 53 = K(,) 53 ⋅3! ⇔ K(,)
53 = ⇔ K(,)
53 =
3!
3!
3! 2!
3! 2!
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
= =
⋅ ⋅
Eksempel 8.11. Antal kombinationer
I en forening skal der blandt 10 kandidater vælges 4 personer til en bestyrelse
På hvor mange forskellige måder kan man sammensætte denne bestyrelse?
Løsning:
Antal måder man kan sammensætte bestyrelsen er
10!
10987 ⋅ ⋅ ⋅
K(10,4) = = = 10⋅3⋅ 7 = 210 måder
4! ⋅6!
4!
TI89: MATH Probability nCr(10,4) . Resultat: = 210
Excel: f x Matematik og trig KOMBIN(10;4) 210

8. Regneregler for sandsynlighed, Kombinatorik
OPGAVER
Opgave 8.1
I en mindre by viser en undersøgelse, at 60% af alle husstande holder en lokal avis, mens 30%
holder en landsdækkende avis. Endvidere holder 10% af husstandene begge aviser.
Lad en husstand være tilfældig udvalgt, og lad A være den hændelse, at husstanden holder en
lokal avis, og B den hændelse, at husstanden holder en landsdækkende avis.
Beregn sandsynlighederne for følgende hændelser.
C: Husstanden holder begge aviser .
D: Husstanden holder kun den lokale avis.
E: Husstanden holder mindst én af aviserne.
F: Husstanden holder ingen avis
G: Husstanden holder netop én avis.
Opgave 8.2
1) I figur 1 er vist et elektrisk apparat, som kun fungerer, hvis enten alle komponenter 1a, 1b og
1c i den øverste ledning eller alle komponenter 2a, 2b og 2c i den nederste ledning fungerer.
Sandsynligheden for at hver komponent fungerer er vist på tegningen, og det antages, at
sandsynligheden for at en komponent fungerer er uafhængig af om de øvrige komponenter
fungerer.
88
1) Hvad er sandsynligheden for at apparatet
i figur 1 fungerer.
2) I figur 2 er vist et andet elektrisk apparat,
som tilsvarende kun fungerer, hvis alle de
tre kredsløb I, II og III fungerer, og det er
kun tilfældet hvis enten den øverste eller
den nederste komponent fungerer.
Hvad er sandsynligheden for at apparatet
i figur 2 fungerer.

89
Opgaver til kapitel 8
Opgave 8.3
Tre skytter skyder hver ét skud mod en skydeskive. De har træfsandsynligheder 0.75, 0.50 og
0.30.
Beregn sandsynligheden for
1) ingen træffere, 2) én træffer, 3) to træffere, 4) tre træffere.
Opgave 8.4
En “terning” har form som et regulært polyeder med 20 sideflader. På 4 sideflader er der skrevet
1, på 8 sideflader er der skrevet 6 mens der er skrevet 2, 3 , 4 og 5 på hver 2 sideflader.
Find sandsynligheden for i tre kast med denne terning at få
1) tre seksere
2) mindst én sekser
3) enten tre seksere eller tre enere
Opgave 8.5
Fire projektgrupper på en virksomhed antages at have sandsynlighederne 0.6, 0.7, 0.8 og 0.9 for at få succes med
deres projekt. Grupperne antages at arbejde uafhængigt af hinanden. Find sandsynligheden for, at
a) alle grupper får succes,
b) ingen grupper får succes,
c) mindst 1 gruppe får succes,
d) i alt netop 1 gruppe får succes,
e) i alt netop 3 grupper får succes,
f) i alt netop 2 grupper får succes.
Opgave 8.6
En klasse med 21 elever skal under en øvelse fordeles på 5 grupper. 4 af grupperne skal være på 4 elever, og 1 gruppe
skal være på 5 elever.
På hvor mange måder kan fordelingen af eleverne på de 5 grupper foregå?
Opgave 8.7
Af en forsamling på 8 kvinder og 4 mænd skal udtages en arbejdsgruppe på 5 personer.
a) Gør rede for, at gruppen kan udvælges på 448 forskellige måder, når det forlanges, at den skal bestå af højst 3
kvinder og højst 3 mænd.
b) Beregn antallet af måder, hvorpå gruppen kan udvælges, når det forlanges, at de 5 personer ikke alle må være af
samme køn.
Opgave 8.8
a) Bestem det antal måder, hvorpå bogstaverne A, B og C kan stilles rækkefølge.
b) Samme opgave for A, B, C og D.
Opgave 8.9.
På et spisekort er opført 6 forretter, 10 hovedretter og 4 desserter.
1) Hvor mange forskellige middage bestående enten af forret og hovedret eller af hovedret og dessert kan man
sammensætte.
2) Hvor mange forskellige middage bestående af en forret, en hovedret og en dessert kan man sammensætte.
Opgave 8.10
Bestem antallet af 5-cifrede tal, der kan skrives med to l-taller, et 2- tal og to 3-taller.

8. Regneregler for sandsynlighed, Kombinatorik
Opgave 8.11
En virksomhed fremstiller en bestemt slags apparater. Hvert apparat er sammensat af 5 komponenter. Heraf er 3
tilfældigt udvalgt blandt komponenter af typen a og 2 blandt komponenter af typen b. Det vides, at 10% af akomponenterne
er defekte og 20% af b-komponenterne er defekte. Et apparat fungerer hvis og kun hvis det ikke
indeholder nogen defekt komponent.
Der udtages på tilfældig måde et apparat fra produktionen. Lad os betragte hændelserne:
A: Det udtagne apparat indeholder mindst 1 defekt a-komponent.
B: Det udtagne apparat indeholder mindst 1 defekt b-komponent.
1) Find P( A), P( B)
og P( A∩B) .
2) Find sandsynligheden for, at et apparat, der på tilfældig måde udtages af produktionen ikke fungerer.
3) Et apparat udtages på tilfældig måde fra produktionen og det konstateres ved afprøvning at det ikke fungerer. Find
sandsynligheden for, at apparatet ikke indeholder nogen defekt a-komponent.
Opgave 8.12
En test består af 40 spørgsmål, der alle skal besvares med ,'ja'. 'nej' og 'ved ikke'. På hvor mange forskellige måder
kan prøven besvares?
Opgave 8.13
I en virksomhed skal der installeres et kaldesystem. I hvert lokale
opsættes et batteri af n lamper, og hver af de ansatte har sin bestemte
lampekombination.
1) Hvis n = 5, hvor mange ansatte kan da have deres eget kaldesystem
(se figuren)
2) Hvis virksomheden har 500 ansatte, hvor stor skal n så være.
Opgave 8.14
Normale personbilers indregistreringsnumre består af to bogstaver og et nummer mellem 20000 og 59999 .
Lad os antage, at man er nået til numre der begynder med UV. Et eksempel på en nummerplade er da UV 54755
Hvad er sandsynligheden for, at en nyindregistreret bil får et registreringsnummer med lutter forskellige cifre, når
vi antager, at alle cifre har samme sandsynlighed?
Opgave 8.15
Hvor mange forskellige telefonnumre på 8 cifre kan man danne, når første ciffer ikke må være nul?
90

91
9.2 Hypergeometrisk fordeling
9. VIGTIGE DISKRETE FORDELINGER
9.1 INDLEDNING
Vi vil i dette kapitel betragte diskrete stokastiske variable, hvis værdier er hele tal.
Vi vil især behandle de diskrete fordelinger:
“Den hypergeometriske fordeling”, “Binomialfordelingen” og “Poissonfordelingen”
9.2 HYPERGEOMETRISK FORDELING
Den “hypergeometriske fordeling”, finder bl.a. anvendelse ved kvalitetskontrol af varepartier
(jævnfør eksempel 9.2), ved markedsundersøgelser, hvor man uden tilbagelægning udtager en
repræsentativ stikprøve på eksempelvis 500 personer
I det følgende eksempel “udledes” formlen for den hypergeometriske fordeling.
Eksempel 9.1. Hypergeometrisk fordeling
I en forening skal der blandt 5 kvindelige og 8 mandlige kandidater vælges en bestyrelse på 4
personer. Find sandsynligheden for, at der er netop 1 kvinde i bestyrelsen..
Løsning:
X = antal kvinder i bestyrelsen
At der skal være netop 1 kvinde i bestyrelsen forudsætter, at vi udtager 1 kvinde ud af de 5
kvinder og 3 mænd ud af de 8 mænd.
At udtage 1 kvinde ud af 5 kvinder kan gøres på K(5,1) måder
At udtage 3 mænd ud af 8 mænd kan gøres på K(8,3) måder.
Antal gunstige udfald er ifølge multiplikationsprincippet K(5,1) ⋅K(8,3)
Det totale antal udfald fås ved at udtage 4 personer ud af de 13 kandidater
Dette kan gøres på K(13,4) måder.
K(,) 51 ⋅ K(,)
83
P( X = 1)
=
K(
13, 4)
TI-89: Vælg MATH\Probability\nCr nCr(5,1) ⋅ nCr(8,3)/nCr(13,4) =0.3916
Excel: Vælg f x Matematik og trig KOMBIN(5;1)*KOMBIN(8;3)/KOMBIN(13;4) =0,391608
Karakteristisk for en hypergeometrisk fordeling er, at elementerne i udfaldsrummet (kugler i en
beholder) kan opdeles i to grupper.
En opdeling kunne som i eksempel 9.1 være kvinder og mænd eller som i kvalitetskontrol være
i defekte varer og ikke-defekte varer.

9. Vigtige diskrete fordelinger
Lad os antage, at vi har en beholder med N kugler, hvoraf de M er røde og resten har en anden
farve.
Der udtrækkes en stikprøve på n kugler uden tilbagelægning.
Lad X være antallet af røde kugler blandt de n kugler.
X er hypergeometrisk fordelt med parametrene N, M, n (kort skrevet h(N,M,n))
P(X = x) er sandsynligheden for at netop x kugler er røde blandt de n udtrukne kugler.
X siges at være hypergeometrisk fordelt med parametrene N, M, n (kort skrevet h(N,M,n))
hvor
K( M, x) ⋅K( N − M, n−x) PX ( = x)
=
K( N, n)
Formlen udledes på samme måde som det skete i eksempel 9.1
Sætte x = 0, 1, 2, ... finder vi forskellige værdier af tæthedsfunktionen.
I “Supplement til statistiske grundbegreber” afsnit 9A bevises, at den hypergeometriske fordeling
N − n
har middelværdien E( X) = n⋅ p og spredningen σ ( X) = n⋅ p⋅( 1−
p) ⋅ , hvor p .
N − 1
M
=
N
Eksempel 9.2: Hypergeometrisk fordeling h (10, 6, 3 ).
I en urne findes 10 kugler, hvoraf 6 er sorte, 4 er hvide.
Vi betragter det tilfældige eksperiment: "Udtrækning af en kugle og observation af farven på
kuglen”. Eksperimentet gentages 3 gange, idet den udtrukne kugle ikke lægges tilbage mellem
hver udtrækning.
Lad X betegne antallet af udtrukne sorte kugler.
Find og skitser tæthedsfunktionen for X, og beregn middelværdi og spredning for X.
LØSNING:
X er en diskret stokastisk variabel, der som er hypergeometrisk fordelt h (10, 6, 3) med
tæthedsfunktionen f (x) = P(X = x):
⎧ K( 60 , ) ⋅ K(
43 , ) 4
⎪
= = 0. 033 for x = 0
K(
10, 3)
120
⎪
⎪
K(,) 61 ⋅ K(,)
42 36
= = 0. 300 for x = 1
⎪ K(
10, 3)
120
⎪
f ( x) = P( X = x)
= ⎨ K( 62 , ) ⋅ K(
41 , ) 60
⎪
= = 0500 . for x = 2
K(
10, 3)
120
⎪
K( 63 , ) ⋅ K(
40 , ) 20
⎪
= = 0167 . for x = 3
⎪ K(
10, 3)
120
⎩⎪
0
ellers
Stolpediagram for h (10, 6, 3).
92

Sættes p er middelværdien og
M
= =
N
6
E( X) = n⋅ p=
3⋅ = .
10
6
10 18
N − n
N − 1
⎛
3 ⎜
⎝
6
10 1
spredningen σ ( X) = n⋅ p⋅( 1−
p) ⋅ = ⋅ ⋅ − = 0.748
93
6 ⎞ 10 − 3
⎟ ⋅
10⎠
10 − 1
9.2 Hypergeometrisk fordeling
Den hypergeometriske fordeling finder bl.a. anvendelse i kvalitetskontrol, hvilket følgende
eksempel viser.
Eksempel 9.3: Stikprøveudtagning (kvalitetskontrol)
En producent fabrikerer komponenter, som sælges i æsker med 600 komponenter i hver.
Som led i en kvalitetskontrol udtages hvert kvarter tilfældigt en æske produceret indenfor de
sidste 15 minutter, og 25 tilfældigt udvalgte komponenter i denne undersøges, hvorefter det
foregående kvarters produktion godkendes, såfremt der højst er én defekt komponent i stikprøven.
Hvor stor er acceptsandsynligheden p, hvis æsken indeholder i alt 10 defekte komponenter,
såfremt udtrækningen sker uden mellemliggende tilbagelægninger ?
Løsning:
X = antal defekte blandt de 25 komponenter
Da partiet godkendes, hvis der enten er 0 defekte eller 1 defekt, følger af additionssætningen at
p = P (X = 0) + P (X = 1).
Hændelsen "X = 0" forudsætter, at vi i alt udtager 0 af de 10 defekte og 25 forskellige af de 590
K( 10, 0) ⋅ K(
590, 25)
ikke-defekte, dvs. P( X = 0)
=
= 06512 . .
K(
600, 25)
Hændelsen "X = 1" forudsætter, at vi i alt udtager 1 af de 10 defekte og 24 forskellige af de 590
K( 10, 1) ⋅ K(
590, 24)
ikke-defekte, dvs. P( X = 1)
=
= 0. 2876 .
K(
600, 25)
Vi har altså p = 0.6512 + 0.2876 = 0.9388 = 93.88%.
TI-89: Vælg MATH\Probability\nCr
(nCr(10,0) nCr(590,25)+nCr(10,1) nCr(590,24))/nCr(600,25) = 0.9388
⋅ ⋅
Excel: Vælg f x Statistik HYPGEOFORDELING Udfyld menu
HYPGEOFORDELING(0;25;10;600)+HYPGEOFORDELING(1;25;10;600) = 0,938876

9. Vigtige diskrete fordelinger
9.3 BINOMIALFORDELING
Binomialfordelingen benyttes som model for antallet af "succeser" ved n uafhængige gentagelser
af et eksperiment, som hver gang har samme sandsynlighed p for "succes".
Problemstillingen fremgår af følgende eksempel.
Eksempel 9.4. En binomialfordelt variabel.
En drejebænk producerer 1 % defekte emner.
Lad X være antallet af defekte blandt de næste 5 emner der produceres.
Vi ønsker at finde sandsynligheden for at finde netop 2 defekte blandt disse 5, det vil sige
P( X = 2)
.
Løsning:
Lad et eksperiment være at udtage et emne fra produktionen.
Resultatet af eksperimentet har to udfald: defekt, ikke defekt.
Eksperimentet gentages 5 gange uafhængigt af hinanden.
Der er en bestemt sandsynlighed for at få en defekt, nemlig p = 0.01.
Lad d være det udfald at få en defekt, og d være det udfald at få en fejlfri.
Vi opskriver nu samtlige forløb, der giver 2 defekte ud af 5
ddddd , , , ,
ddddd , , , ,
ddddd , , , ,
ddddd , , , ,
ddddd , , , ,
ddddd , , , ,
ddddd , , , , .
ddddd , , , ,
ddddd , , , ,
ddddd , , , ,
Da eksperimenterne gentages uafhængigt af hinanden, følger det af produktsætningen (både -og),
at det første forløb må have sandsynligheden
2 3
0. 01⋅0. 01⋅( 1−0. 01) ⋅( 1−0. 01) ⋅( 1− 0. 01) = 0. 01 ⋅( 1−0. 01)
.
Det næste forløb må have sandsynligheden
2 3
001 . ⋅( 1−001 . ) ⋅001 . ⋅( 1−001 . ) ⋅( 1− 001 . ) = 001 . ⋅( 1−001 . )
Vi ser, at alle gunstige forløb har samme sandsynlighed.
Antal forløb må være lig antal måder man kan placere 2 d’er på 5 tomme pladser (eller antal
måder man kan tage 2 kugler ud af en mængde på 5).
Dette ved vi kan gøres på K(5,2)=10 måder (svarende til de 10 forløb).
2 3
Vi får følgelig, at p = K(,)
52 ⋅001 . ⋅( 1− 001 . ) = 000097 .
TI-89: CATALOG\F3\binomPdf(5, 0.01,2) = 0.00097
Excel: Vælg f x Statistik BINOMIALFORDELING Udfyld menu BINOMIALFORDELING(2;5;0,01;0) =
0,00097
94

95
9.3 Binomialfordelingen
DEFINITION af binomialfordeling.
1) Lad et tilfældigt eksperiment have 2 udfald “succes” og “fiasko”
2) Lad eksperimentet blive gentaget n gange uafhængigt af hinanden, og lad
sandsynligheden for succes være en konstant p
Lad X være antallet af succeser blandt de n gentagelser
X er en diskret stokastisk variabel med tæthedsfunktionen
⎧
x n−x ⎪Knx
( , ) ⋅p⋅( 1− p) f ( x) = P( X = x)
= ⎨
⎩⎪ 0
X siges at være binomialfordelt b ( n, p).
for
ellers
x∈{ 012 , , ,..., n}
I eksemplet har vi “udledt” den såkaldte binomialfordeling, som er defineret på følgende måde:
SÆTNING 9.1. (middelværdi og spredning for binomialfordeling).
Lad X være binomialfordelt b (n, p).
Der gælder da E ( X )= n ⋅ p
og σ σ ( X ) = n ⋅ p ⋅ ( 1
−
p
)
. .
Bevis:
Lad os betragte et eksperiment, hvor resultatet “succes” har sandsynligheden p for at ske.
Lad os foretage n uafhængige gentagelser af eksperimentet. At gentagelserne er uafhængige betyder, at udfaldet
af et eksperiment ikke afhænger af udfaldet af de forrige eksperimenter.
Lad os betragte n stokastiske variable X1, X2,..., Xn, hvor X i = ⎧1 hvis i' te gentagelse af eksperimentet giver succes.
⎨
⎩0
ellers
Vi har E( Xi) = ∑ xi f ( xi) = 1⋅ p+ 0⋅( 1−
p) = p,
og
i
2 2 2 2
V( Xi) = ∑ ( xi − µ ) f ( xi) = ( 1− p) ⋅ p+ ( 0− p) ⋅( 1− p) = p− p = p⋅( 1−
p)
i
Idet X = X1 + X2 + ... + Xner binomialfordelt b ( n, p) fås af linearitetsreglen (kapitel 1afsnit 5), at
E( X) = E( X1) + E( X2) + E( X3) + ... + E( Xn) = p+ p+ p+ ... + p= n⋅ p.
Endvidere fås af kvadratreglen i kapitel 1 afsnit 5, idet vi har uafhængige gentagelser, at
V( X) = V( X1) + V( X2) + ... + V( Xn) = p⋅( 1− p) + p⋅( 1− p) + ... + p⋅( 1−
p)
,
eller V( X) = n⋅ p⋅( 1 − p)
.

9. Vigtige diskrete fordelinger
Eksempel 9.5: Tæthedsfunktion for binomialfordelt variabel .
Lad der på to af sidefladerne på en terning være skrevet tallet 1, på to andre sideflader være
skrevet tallet 2 og på de sidste to sideflader være skrevet tallet 3.Vi betragter det tilfældige
eksperiment:
"7 kast med en terningen og observation af det fremkomne tal.
Lad X betegne antallet af toere ved de 7 kast. X antages at være binomialfordelt b( 7 ) . 1 , 3
1) Angiv tæthedsfunktionen f (x) for X (3 betydende cifre), og tegn et stolpediagram for f (x).
2) Find middelværdi og spredning for X
En person foretager eksperimentet 11 gange, d.v.s. foretager 11 gange en serie på 7 kast med
terningen. Stikprøven gav følgende resultat
Antal toere i en serie 0 1 2 3 4 5 6 7
Antal gange dette skete 1 2 4 3 1 0 0 0
3) Giv på grundlag af stikprøven et estimat for p i binomialfordelingen.
4) Giv på grundlag af stikprøven et estimat for middelværdi og spredning
Løsning:
x n x
1) f ( x) = P( X = x) = K( , x)
⋅ ⎛
⎜
⎝
⎞
−
1 ⎛ ⎞
7 ⎟ ⋅⎜1− ⎟
3⎠
⎝ ⎠
1
3
TI89: binomPdf(7,1/3,x) x = 0 og derefter x = 1 osv.
Excel:BINOMIALFORDELING(0;7;1/3;0), og derefter BINOMIALFORDELING( 1;7;1/3;0) osv.
⎧0059
. for x = 0
⎪
⎪
205
⎪0307
.
⎪
⎪0.
256
⎪
f ( x) = P( X = x)
= ⎨0128
.
⎪0.
038
⎪
⎪0.
006
⎪
⎪
0. 000
⎩⎪
for
for
for
for
for
for
for
ellers 0
x = 1
x = 2
x = 3
x = 4
x = 5
x = 6
x = 7
0
Stolpediagram for binomialfordelingen
2) E( X) = n⋅ p=
7 ⋅ = . og
1
⎛ ⎞
233 σ ( X) = n⋅ p⋅( 1− p)
= 7⋅ ⋅⎜− ⎟ = .
3
⎝ ⎠
1
1
3
1
125
3
3) Der er i alt 10 ⋅ + 21 ⋅ + 42 ⋅ + 33 ⋅ + 14 ⋅ = 23 toere i 77 kast.
23
Et estimat for p er p $ = = 0299 .
77
23
4) Stikprøvens middelværdi er x = = 209 . , og stikprøvens spredning er
11
⎛ ⎞
σ ( X) = n⋅ p⋅( 1− p)
= 7⋅ ⋅⎜− ⎟ = .
⎝ ⎠
23 23
1 121
77 77
96

97
9.3 Binomialfordelingen
Hypotesetest for binomialfordelt variabel.
I kapitel 6 gennemgik vi ved en række eksempler de grundlæggende begreber for
hypotesetestning for én normalfordelt variabel. Disse begreber kan uændret overføres til
hypotesetestning for binomialfordelt variabel.
Konfidensintervaller.
Som beskrevet i appendix er det ofte muligt at approksimere med en normalfordeling.
Derved fremkommer de formler som er beskrevet i appendix 4.1 punkt 5.
Kan approksimationen ikke anvendes, kan man ved løsning af en passende ligning finde de
eksakte grænser for konfidensintervallerne. Da det er ret besværligt, foretrækkes så vidt muligt
(selv i statistikprogrammer) at anvende approksimationen med normalfordelingen.
De følgende to eksempler viser anvendelser heraf.
Eksempel 9.6. Ensidet binomialfordelingstest.
En levnedsmiddelproducent fremstiller et levnedsmiddel A, som imidlertid har en ret ringe
holdbarhed. Efter en række eksperimenter lykkedes det at frembringe et produkt B, som i alt
væsentligt er identisk med A, men som har en bedre holdbarhed. Af markedsmæssige grunde er
det vigtigt, at der ikke er forskel på smagen af B og af det velkendte produkt A. For at undersøge
dette, lader producenten et panel af 24 ekspertsmagere vurdere, om man kan smage forskel. Man
foretog derfor følgende smagsprøvningseksperiment.
Hver ekspertsmager fik 3 ens udseende portioner, hvoraf en portion var af det ene levnedsmiddel
og de to andre portioner var af det andet levnedsmiddel.
Hvilket af de 3 portioner der skulle indeholde et andet levnedsmiddel end de to andre, og om det
skulle være levnedsmiddel A eller B , afgjordes hver gang ved lodtrækning. Kun forsøgslederen
havde kendskab til resultatet.
Hver ekspertsmager fik besked på, at de skulle fortælle forsøgslederen hvilken af de tre portioner
der smagte anderledes. Hvis man ikke kunne smage forskel, skulle man gætte.
Resultatet viste, at af de 24 svar var 13 svar rigtige.
1
Ved ren gætning kunne man forvente ca. 3 dvs. ca. 8 rigtige svar. 13 rigtige svar er betydeligt
flere, men kan det alligevel tilskrives tilfældigheder ved gætning?
Kan der på et signifikansniveau på 5% statistisk påvist, at ekspertsmagerne kan smage forskel
på smagen af A og B?
Løsning:
Lad X = antallet af rigtige svar.
X er binomialfordelt b (n, p), hvor n = 24 og p er ukendt.
1
Nulhypotese H0: p = mod den alternative hypotese Hp : >
3
1
3
TI89: P - værdi = P( X ≥ 13)
= binomCdf(24, 1/3, 13, 24) = 0.0284 = 2.84%
Excel: P - værdi = 1− P( X ≤12)
= 1-BINOMIALFORDELING(12;24;1/3;1) = 0,028441
Da P - værdi < 5% forkastes nulhypotesen (enstjernet), dvs. der må konkluderes, at der er en
smagsforskel mellem produkt A og B.

9. Vigtige diskrete fordelinger
Eksempel 9.7. Konfidensinterval for parameteren p i binomialfordeling.
En plastikfabrik har udviklet en ny type affaldsbeholdere. Man overvejer at give en 6 års garanti
for holdbarheden. For at få et skøn over om det er økonomisk rentabelt, bliver 100 beholdere
udsat for et accelereret livstidstest som simulerer 6 års brug af beholderne. Det viste sig, at af de
100 beholdere overlevede de 85 testen.
Idet antallet af overlevende beholdere antages at være binomialfordelt, skal man
1) Angive et estimat for sandsynligheden p for at en beholder “overlever” i 6 år .
2) Angive et 95% konfidensinterval for p.
Løsning:
1) Lad X være antallet af “overlevende” beholdere.
X forudsættes binomialfordelt b (100, p).
Appendix 4.1 punkt 5 anvendes. Et estimat for p er ~ x 85
p = = = 085 .
n 100
2) Da 10 ≤ x ≤n−10 er forudsætningerne for at benytte normalfordelingsapproksimation opfyldt.
Vi får:
~
~ p⋅( 1−
~ p)
085 . ⋅( 1−085 . )
p ± u α ⋅
= 085 . ± 196 . ⋅
= 085 . ± 007 .
− n
100
1 2
dvs. 078 . ≤ p ≤092
.
TI 89 og Excel benytter denne formel, dvs. man skal altid først undersøge om forudsætningen
er opfyldt.
TI89: APPS\STATS/List\F7\5:1-PropZInt\ENTER
Menuen udfyldes med x: 85 n: 100 C-level: 0.95 ENTER
Resultat: C Int : [0.78 ; 0.92 ]
Excel:
radius= NORMINV(0,975;0;1)*KVROD(0,85*(1-0,85)/100) 0,069985
Nedre grænse 0,85-I3 0,780015
Øvre grænse 0,85+I3 0,919985
Eksakt løsning:
Er betingelsen ikke opfyldt (eller vil man have det “eksakte” resultat) benyttes formel i appendix 4.1 nr 6.
Øvre grænse: Løs ligningen P( X ≤ 85)
= 0.025 med hensyn til p.
TI89: solve(binomCdf(100, p,0,85)=0.025,p) p > 0 Resultatet blev p = 0.914.
Nedre grænse: Løs ligningen P( X ≥ 85)
= 0.025 med hensyn til p.
TI89: solve(binomCdf(100, p,85,100)=0.025,p) p > 0 Resultatet blev p = 0.765.
95% Konfidensinterval: [0.765; 0.914]
Bemærk, at konfidensintervallet ikke ligger helt symmetrisk omkring 0.85, da binomialfordelingen ikke er
helt symmetrisk omkring 0.85
Forklaring på formlen:
Udenfor et 95% konfidensinterval ligger 5%, og af symmetrigrunde ligger der 2,5% på hver side. (jævnfør
figuren)
Jo større den sande værdi p er i forhold til 0.85 jo mindre bliver sandsynligheden for at 85 eller færre
overlevede testen. Vi leder derfor i grænsen efter et p > 0.85 , så P( X ≤ 85)
= 0.025.
Dernæst findes nedre grænse ved at lade p falde, indtil PX ( ≥ 85) ≈ 0. 025
Bestemmelse af stikprøvens størrelse
98

99
9.3 Binomialfordelingen
Før man starter sine målinger, kunne det være nyttigt på forhånd at vide nogenlunde hvor
mange målinger man skal foretage, for at få resultat med en given nøjagtighed.
Hvis man antager, at man kan approksimere med normalfordelingen, ved vi, at radius for et
p$ ⋅( 1−
p$)
95% konfidensinterval er r = u0975
. ⋅
.
n
Løses denne ligning med hensyn til n fås
u
n = p p
r
⎛ 0975 . ⎞
⎜ ⎟ $ ⋅( 1−
$)
⎝ ⎠
2
Det grundlæggende problem er her, at man næppe kender $p eksakt.
Man kender muligvis på basis af tidligere erfaringer størrelsesordenen af $p . Hvis ikke
kunne man eventuelt udtage en lille stikprøve, og beregne et $p på basis heraf.
Endelig er der den mulighed, at sætter $p = 0.5, som er maksimumsværdien af p$ ⋅( 1−
p$)
Benyttes denne værdi får man den størst mulige værdi af n for en given værdi af r.
Ulempen er, at dette fører til en større stikprøvestørrelse end nødvendigt.
Det følgende eksempel illustrerer fremgangsmåden.
Eksempel 9.8. Bestemmelse af antal i stikprøve.
I en opinionsundersøgelse vil man spørge et repræsentativt antal vælgere om hvilket parti de
vilde stemme på, hvis der var valg i morgen.
I denne undersøgelse ønskes inden udtagning af stikprøven, at antallet skal være så stort, at
radius i konfidensintervallet højst er 2%.
Løsning:
Metode 1. For at få en øvre grænse, sættes $p = 0.5.
2 2
Vi får
u
n = p p
r
⎛ ⎞
⎜ ⎟ ⋅ − =
⎝ ⎠
⎛
0975 . 196 . ⎞ 1 1
$ ( 1 $) ⎜ ⎟ ⋅ = 2401
⎝ 002 . ⎠ 2 2
Metode 2 Da man på forhånd ved, at ved sidste valg fik ingen partier mere end 30% af
stemmerne sættes $p = 0.3.
2 2
u
n = p p
r
⎛ ⎞
⎜ ⎟ ⋅ − =
⎝ ⎠
⎛
0975 . 196 .
$
⎞
( 1 $) ⎜ ⎟ 03 . ⋅ 07 . = 2017
⎝ 002 . ⎠

9. Vigtige diskrete fordelinger
Approksimation af hypergeometrisk fordeling med binomialfordeling.
At erstatte den hypergeometriske fordeling h (N, M, n) med binomialfordelingen b (n, p) vil
for de fleste anvendelser kunne gøres med en passende nøjagtighed, hvis stikprøvestørrelsen n
N n 1
er mindre end eller lig 10% af partistørrelsen N ( n ≤ ⇔ ≤ ).
10 N 10
I så fald sættes i binomialfordelingen p .
M
=
N
Eksempel 9.9. Approksimation af hypergeometrisk fordeling til binomialfordeling.
I eksempel 9.3, hvor man udtog 25 komponenter fra æsker på 600 komponenter, skete
udtagningen logisk nok uden tilbagelægning. Imidlertid er det klart, at da æskerne indeholder
mange komponenter vil sandsynligheden for at få en defekt ikke ændrer sig meget, hvis man i
stedet havde foretaget udtagningen med tilbagelægning.
Der blev antaget, at der var 10 defekte i en sådan æske med 600, og dette antal defekte vil så
være konstant, under hver udtrækning.
10 1
Vi har derfor, at P(at få en defekt) = = . Betingelserne for at benytte
600 60
binomialfordelingen er nu til stede.
Løsningen af problemet i eksempel 9.3 vil derfor nu være:
TI89: pa = P( X ≤ 1) = P( X = 0) + P( X = 1)
= binomCdf(25,1/60,0,1) = 0.9353
Det ses, at vi får praktisk samme resultat som i eksempel 9.3.
9.4 POISSONFORDELINGEN
Poissonfordelinger benyttes ofte som statistisk model for antallet af "impulser" pr. tidsenhed.
Disse impulser antages at komme tilfældigt og uafhængigt af hinanden.
Som eksempler kan nævnes: Antal trafikuheld på en bestemt vejstrækning i løbet af et år,
antal biler, der passerer en militær kontrolpost, antal varevogne der ankommer pr. time til et
stort varehus og antal telefonsamtaler der føres fra en telefoncentral, der er oprettet under en
øvelse.
Modellen kan dog også anvendes på andet end pr. tidsenhed, eksempelvis også på antal
revner pr. km kabel, hvis disse revner forekommer tilfældigt og uafhængigt af hinanden.
Under sådanne omstændigheder kan man ofte benytte den i det følgende omtalte
Poissonfordeling som statistisk model for antallet af "impulser" pr. tidsenhed eller
volumenenhed eller længdeenhed osv.
100

101
9.4 Poissonfordelingen
SÆTNING 9.2 (Poissonfordeling). Lad X være en stokastisk variabel, som angiver antallet
af impulser i et givet tidsrum (eller areal, volumen, produktionsenhed osv.), idet ethvert
tidspunkt i tidsrummet har samme mulighed for at være impulstidspunkt som ethvert andet
tidspunkt. Endvidere skal impulserne indtræffe tilfældigt og uafhængigt af hinanden * ) .
Hvis det gennemsnitlige antal impulser i tidsrummet er µ > 0 , så siges X at være
Poissonfordelt p ( µ ) med sandsynlighedsfordelingen (tæthedsfunktionen) f(x) = P(X = x)
bestemt ved
⎧ x
⎪
µ − µ
f ( x) = P( X = x) =
⋅e for x ∈{,,,...}
012
⎨ x!
⎩
⎪ 0 ellers
Middelværdien for p( µ ) er E ( X ) = µ og spredningen er σ ( X ) = µ .
I formuleringen af de ovennævnte betingelser kan efter behov "et lille tidsrum ∆ t" erstattes
med "en lille længde ∆ l ", "et lille areal ∆ A" eller "et lille volumen ∆ V".
*) Præcis formulering: Følgende 3 betingelser skal være opfyldt:
1) Sandsynligheden for netop én impuls i et meget lille tidsrum ∆ t er med tilnærmelse proportional med ∆ t
.
P( X = 1)
(Matematisk formulering lim = λ ( λ er en positiv konstant)
∆t→0 ∆t
2) Sandsynligheden for 2 eller flere impulser i det meget lille tidsrum ∆ t er lille sammenlignet med ∆ t .
P( X > 1)
(Matematisk formulering lim = 0 )
∆t→0 ∆t
3) Antal impulser i forskellige, ikke overlappende tidsrum er statistisk uafhængige.
En bevisskitse for sætningen kan ses i “Supplement til statistiske grundbegreber” afsnit
9.C.
Eksempel 9.10: Antal revner p. meter i et tyndt kobberkabel.
På en fabrik fremstilles kobberkabler af en bestemt tykkelse. Mikroskopiske revner
forekommer tilfældigt langs disse kabler. Man har erfaring for, at der i gennemsnit er 12.3 af
den type revner p. 10 meter kabel.
Beregn sandsynligheden for, at der
1) ingen ridser er i 1 meter tilfældigt udvalgt kabel.
2) er mindst 2 ridser i 1 meter tilfældigt udvalgt kabel.
3) er højst 4 ridser i 2 meter tilfældigt udvalgt kabel
Fabrikken går nu over til en anden og billigere produktionsmetode. For at få et estimat for
middelværdien ved den nye metode måltes antallet af revner på 12 kabelstykker på hver 10
meter.
Resultaterne var
Kabel nr. 1 2 3 4 5 6 7 8 9 10 11 12
Antal revner 8 4 14 6 8 10 10 16 2 2 6 8
4) Angiv på basis heraf et estimat for middelværdien af antal revner pr. 10 m kabel.

Vigtige diskrete fordelinger
Løsning:
X = antal revner i 1 meter kabel.
X antages Poissonfordelt p ( µ ). (idet vi med tilnærmelse kan antage, at betingelserne i
sætning 9.2 er opfyldt (impuls er her ridser).
12. 3
Da det gennemsnitlige antal revner pr. 1m kabel er µ = = 123 . fås:
10
0
123 . −123
.
1) P( X = 0)
= ⋅ e = 0. 292 .
0!
TI89: PoissPdf(1.23,0) = 0.292
Excel: POISSON(0;1,23;0) =0,292293
2) TI-89: P( X ≥ 2) = 1− P( X ≤ 1)
= 1-PoissCdf(1.23, 0, 1) = 0.3482
Excel: P( X ≥ 2) = 1− P( X ≤ 1)
= 1 - POISSON(1;1,23;1) = 0,348188
3) Y = antal revner i 2 meter kabel.
Da der i gennemsnit er 2,46 revner i 2 meter kabel, er 2.46 et estimat for µ .
Vi har derfor TI89: = poissCdf(2.46, 0, 4) = 0.8965
P( X ≤ 4)
Excel: P( X ≤ 4)
=POISSON(4;2,46;1) = 0,896458
4) Der er i alt 94 revner i 12 kabelstykker på hver 10 meter. Et estimat for µ er derfor
~ 94
µ = = 783 . .
12
Hypotesetest for Poissonfordelt variabel.
I kapitel 5 gennemgik vi ved en række eksempler de grundlæggende begreber for
hypotesetestning for én normalfordelt variabel. Disse begreber kan uændret overføres til
hypotesetestning for Possonfordelt variabel.
Har man rådighed over en lommeregner med kumuleret Poissonfordeling kan testene
gennemføres eksakt. (se appendix 5.5)
Konfidensintervaller.
Som beskrevet i næste afsnit er det ofte muligt at approksimere med en normalfordeling.
Derved fremkommer de formler som er beskrevet i appendix 4.1 punkt 5.
Eksempel 9.11. Ensidet Poissontest.
I eksempel 9.8 betragtede vi mikroskopiske revner i et kobberkabel. Fabrikken gik over til en
anden og billigere produktionsmetode.
1) Test, om den nye metode giver færre revner end den gamle metode.
2) Forudsat, den nye metode giver signifikant færre revner end den gamle metode, skal man
2a) Angiv et 95% konfidensinterval for middelværdien µ af antal revner pr. 120 meter
kabel .
2b) Angiv et 95% konfidensinterval for middelværdien µ 1 af antal revner pr. 10 meter
kabel.
102

103
9.6 Polynomialfordelingen
Løsning:
1) Lad X betegne antallet af revner i 120 meter kabel ved ny metode
X antages Poissonfordelt p( µ ) , hvor vi i eksempel 9.8 fandt at et estimat for µ var
~
µ = 94 .
Ved gammel metode er antal revner i 120 m kabel i middel 12. 3⋅ 12 = 147. 6
Nulhypotese H0: µ = 147. 6 mod den alternative hypotese H: µ < 147. 6 .
TI89:P - værdi = PY ( ≤ 94)
= PoissCdf(147.6, 0 , 94) = 0.000002
Excel:P - værdi = PY ( ≤ 94)
= Poisson(94;147,6;1) = 1,52403E-06
Da P - værdi < 0.05 forkastes nulhypotesen (stærkt) ,dvs. vi er sikre på, at middelantallet af
revner er blevet formindsket ved at anvende den nye metode
2a) Idet m= 94>10 kan formel 6 i appendix 4.1 anvendes.
Antal revner pr 120 m kabel:
Idet
94
x = = 94
1
er et 95% konfidensinterval for µ
x ± u0.
975 ⋅
x
= 94 ± 196 . ⋅
n
94
1
2b) Antal revner pr 10 m kabel:
⎡75
113⎤
⎢ ; [ 625 . ; 941 . ]
⎣12
12 ⎥
⎦
=
. [75 ; 113].
9.5 Den generaliserede hypergeometriske fordeling.
Den hypergeometriske fordeling benyttes som model ved stikprøveudtagning uden tilbagelægning, hvor hvert
element har enten en bestemt egenskab (defekt) eller ikke har denne egenskab (ikke defekt). Hvis der foreligger
flere end to egenskaber, f.eks. udtagning af møtrikker, hvis diameter enten tilhører et givet toleranceinterval eller
er for stor eller for lille, kan man generalisere den hypergeometriske fordeling. Dette illustreres ved følgende
eksempel:
Eksempel 9.12. Generaliseret hypergeometrisk fordeling.
I en urne findes 12 kugler, hvoraf 5 er sorte, 4 er hvide og 3 er røde.
Vi betragter det tilfældige eksperiment: "Udtrækning af 6 kugler uden tilbagelægning og observation af farven
på kuglerne”. Beregn sandsynligheden for at få 2 sorte, 3 hvide og 1 rød kugle.
LØSNING:
Lad X1 være antallet af sorte kugler, X2 være antallet af hvide kugler og X3 være antallet af røde kugler.
Analogt med begrundelsen for den hypergeometriske fordeling fås:
K(,) 52 ⋅K(,) 43 ⋅K(,)
31 10⋅ 4 ⋅ 3
P( X1 = 2, X2 = 3, X3
= 1)
=
= =
013 .
K(
12, 6)
924

Vigtige diskrete fordelinger
9.6 Polynomialfordelingen.
Binomialfordelingen benyttes som model ved uafhængige gentagelser af samme eksperiment. Eksperimentet har
to udfald succes eller ikke succes og der er en konstant sandsynlighed for succes. Hvis der foreligger flere end to
udfald, f.eks. udtagning af møtrikker fra en løbende produktion, hvor diameter enten tilhører et givet
toleranceinterval eller er for stor eller for lille, kan man generalisere til polynomialfordelingen. Idet formlen for
binomialfordelingen kan skrives
n x n x n!
x n x n!
x x
f ( x)
= p ( p)
p ( p)
p p , hvor
x
x!( n x)!
x ! x !
⎛
⎜
⎝
⎞
− −
1 2
⎟ ⋅ ⋅ 1− =
⋅ ⋅ 1−
= ⋅ 1 ⋅ 2
⎠
⋅ −
⋅
p1 + p2
= 1 og x1 + x2 = n fås analogt
104
1 2
DEFINITION af polynomialfordeling.
p1 + p2+ ... + pk= 1 x + x + ... + x = n
Lad n være et positivt helt tal, og lad og hvor alle pér er positive tal
1 2
og alle xér er hele tal.
Sandsynlighedsfordelingen for en polynomialfordelt stokastisk variabel er
( X1, X2,..., Xk) n!
x1 x2
P( X1 = x1, X2 = x2,..., Xk = xk)
=
p1 ⋅ p2 ⋅... ⋅p
x ! ⋅x ! ⋅... ⋅x
!
1 2
Dette illustreres ved følgende eksempel:
Eksempel 9.11. Polynomialfordelingen
En stor produktion af glaskugler indeholder 40% sorte, 35% hvide og 25% røde kugler.
Vi betragter det tilfældige eksperiment: "Udtrækning af 6 kugler observation af farven på kuglerne”.
Beregn sandsynligheden for at få 2 sorte, 3 hvide og 1 rød kugle.
LØSNING:
Lad X1 være antallet af sorte kugler, X2 være antallet af hvide kugler og X3 være antallet af røde kugler.
6!
2 3 1
Vi får nu P( X1 = 2, X2 = 3, X3
= 1)
= 0. 4 ⋅0. 35 ⋅ 0. 25 = 01029 .
2! ⋅3! ⋅1!
9.7 APPROKSIMATIONER
Vi har undertiden benyttet os af, at det under visse forudsætninger er muligt med en rimelig
nøjagtighed, at foretage approksimationer, f.eks. at approksimere en binomialfordeling eller
en Poissonfordeling med en normalfordeling.
Dette kan give nogle simplere beregninger, eksempelvis når man approksimerer en
hypergeometrisk fordeling med en binomialfordeling eller når man ved udregning af
konfidensintervaller for binomialfordeling approksimerer med normalfordeling.
I appendix 9.1 er angivet en samlet oversigt over de mulige approksimationer.
k
k
xk k

9.8. OVERSIGT over centrale formler i kapitel 9
9.8 Oversigt over centrale formler i kapitel 9
X er binomialfordelt bnp ( , ) , hvor n er kendt og p ukendt. Givet stikprøveværdi x
Konfidensinterval
Forudsætninger Estimat for parameter 100 (1 - α ) % konfidensinterval for parameter
10 ≤ x ∧
x ≤n−10 For p: ~ p =
x
n
~ p − u ⋅
105
~ p( 1−~ p)
~
~
p( 1−~
p)
≤ p ≤ p + u ⋅
n
n
α α
1− 1− 2
2
TI89: F7: 1-prop Z-interval
Excel: Se eksempel 9.7
eksakt α
nedre grænse:Løs ligning P( X ≥ x)
= 1− med hensyn til p.
2
øvre grænse: Løs ligning P( X ≤ x)
= α − med hensyn til p
Test af parameter p for binomialfordelt variabel
Der foreligger en stikprøve på X . Observeret stikprøveværdi x. Signifikansniveau er α .
Y er binomialfordelt bnp ( , ) , hvor er en given konstant.
Alternativ
hypotese H
H p p
: > 0 P Y x
H: p< p0
H: p p
0
p 0
P - værdi Beregning H 0 forkastes
( ≥ )
TI89:binomCdf(n, p0, x, ∞ )
Excel:1-Binomialfordeling(x-1;n;p,1) P-værdi < α
P( Y ≤ x)
TI89:binomCdf(n, p0,- ∞ , x)
Excel: Binomialfordeling(x;n;p;1)
P( Y ≥ x)
P( Y ≤ x)
x > n⋅ p0
for x ≤ n⋅ p0
= 0 for
som række 1
som række 2
1 2
P-værdi < 1
2 α

Vigtige diskrete fordelinger
X er Poissonfordelt p( µ ) , hvor µ ukendt. Stikprøve er af størrelsen n, og der optælles i alt m impulser
Konfidensinterval
Forudsætninger Estimat for parameter 100 (1 - α ) % konfidensinterval for parameter
m ≥ 10
For :
µ x m
= x
n x − u α ⋅ ≤ µ ≤ x + u α ⋅
− n
−
Test af parameter µ for Poissonfordelt variabel .
Der foreligger en stikprøve på X af størrelsen n med gennemsnit x . Signifikansniveau er α .
Y er Poissonfordelt pn ( ) , hvor er en given konstant.
Alternativ
hypotese H
H: µ µ
H: µ µ
H: µ ≠ µ 0
> 0 PY n x
⋅ µ 0
µ 0
106
1 2
P - værdi Beregning på TI 89 H 0 forkastes
( ≥ ⋅ )
TI89: poissCdf ( n⋅µ 0 , n⋅x, 1000)
Excel: 1-Poisson( n x -1; ;1)
< 0 PY n x
1 2
⋅ n⋅ µ 0
( ≤ ⋅ )
poissCdf ( n⋅µ 0 , 0,
n⋅x) Excel: Poisson( n x ; ;1)
≥ ⋅µ 0
< ⋅µ 0
PY ( ≥n⋅x) for x n
PY ( ≤n⋅x) for x n
som række 1
som række 2
⋅ n⋅ µ 0
x
n
P - værdi
< α
P-værdi < 1
2 α

OPGAVER
107
APPENDIX 7.1
Opgave 9.1
Ved en lodtrækning fordeles 3 gevinster blandt 25 lodsedler. En spiller har købt 5 lodsedler.
1) Beregn sandsynligheden for at spilleren vinder netop én gevinst.
Lad den stokastiske variable X være bestemt ved
X = Spilleren vinder x gevinster
2) Find og skitser tæthedsfunktionen for X
3) Beregn middelværdien for X
Opgave 9.2
I en urne findes 2 blå, 3 røde og 5 hvide kugler. 3 gange efter hinanden optages tilfældigt en
kugle fra urnen uden mellemliggende tilbagelægning.
1) Find sandsynligheden for hændelsen A, at der højst optages 2 hvide kugler,
2) Find sandsynligheden for, at de tre kugler har samme farve,
Opgave 9.3
En fabrikant fremstiller en bestemt type radiokomponenter. Disse leveres i æsker med 30
komponenter i hver æske. En køber har den aftale med fabrikanten, at hvis en æske
indeholder 4 defekte komponenter eller derover, kan køberen returnere æsken, i modsat fald
skal den godkendes. Køberen kontrollere hver æske ved en stikprøve, idet han af æsken
udtager 10 komponenter tilfældigt. Lad X være antal defekte i stikprøven. Der overvejes nu to
planer:
1) Hvis X = 0, så godkendes æsken, ellers undersøges æsken nærmere.
2) Hvis X ≤ 1,
så godkendes æsken, ellers undersøges æsken nærmere.
Hvad er sandsynligheden for, at en æske, der indeholder netop 4 defekte komponenter, bliver
godkendt af køberen ved metode 1 og ved metode 2.
Opgave 9.4
En tipskupon har 13 kampe med 3 mulige tegn - 1, x og 2 - for hver kamp. En person
bestemmer tegnet, der skal sættes for hver kamp, ved tilfældig udtrækning af en seddel fra 3
sedler med tegnene henholdsvis 1, x og 2.
Angiv sandsynligheden for, at personen opnår netop 8 rigtige tippede kampe på sin kupon.
Opgave 9.5
I et elektrisk specialapparat indgår 30 komponenter, som hver er indkapslet i et heliumfyldt
hylster. Beregn, idet sandsynligheden for, at et komponenthylster lækker, er 0.2%,
sandsynligheden for, at mindst ét af de 30 komponenthylstre lækker.
Opgave 9.6
En “sypigetipper” (M/K) deltog i tipning 42 gange i løbet af et år. På hver tipskupon var der
13 kampe, ved hver af hvilke tipperen ved systematisk gætning satte et af de 3 tegn: 1, x, 2.
Beregn sandsynligheden p for, at tipperen det pågældende år tippede mindst 200 kampe
rigtigt.
Opgave 9.7
Blandt familier med 3 børn udvælges 50 familier tilfældigt. Angiv sandsynligheden for, at der
i mindst 8 af disse familier udelukkede er børn af samme køn.

Vigtige diskrete fordelinger
Opgave 9.8.
Ved en fabrikation af plastikposer leveres disse i æsker med 100 poser i hver. Ved en
godkendelseskontrol af et parti plastikposer udtages og undersøges en tilfældigt udtaget æske,
og partiet godkendes, såfremt æsken højst indeholder én defekt pose.
Vi antager, at den løbende produktion af poser er således, at hver produktion med
sandsynligheden 2% giver en pose, der er defekt; vi vil senere formulere dette således, at
produktionen er i statistisk kontrol med fejlsandsynligheden p = 2%.
Hvor stor er sandsynligheden for, at partiet under disse omstændigheder accepteres?
Opgave 9.9
Det er oplyst, at der for en given vaccine er 80% sandsynlighed for, at den ved anvendelse har
den ønskede virkning.
På et hospital foretoges vaccination af 100 personer med den pågældende vaccine.
Beregn sandsynligheden for, at 15 eller færre af de foretagne vaccinationer er uden virkning.
Opgave 9.10
En ny vaccine formodes med en sandsynlighed på mindst 85% at have en forebyggende
virkning over for en bestemt influenzatype.
Før en truende influenzaepedemi vaccineres et hospitalspersonale på 600 personer med den
pågældende vaccine. 125 af disse bliver smittet af sygdommen.
Kan dette opfattes som en eksperimentel påvisning af, at vaccinen er mindre virksom end
ventet?
Opgave 9.11
1) Antag, at en vis type af fostermisdannelse normalt forekommer med hyppigheden 164
tilfælde p. 100000 fødsler. Beregn sandsynligheden for 3 eller flere fostermisdannelser
blandt 256 fødsler.
2) For at undersøge om forholdene i et bestemt arbejdsmiljø forøger hyppigheden af denne
type misdannelse, undersøgte man hyppigheden af misdannelser for mødre, som under
graviditeten havde haft den aktuelle type af arbejde, og fandt 3 misdannelser blandt 256
fødsler. Kan den forøgede relative hyppighed i dette materiale skyldes tilfældigheder?
Opgave 9.12
Udsættes planterne af en bestemt sort roser for meldugssmitte, bliver i middel brøkdelen p
angrebet, hvor p er mindst 0.20. En rosengartner fremavler en rosenstamme, som han påstår
er mere modstandsdygtig over for meldugssmitte. For at kontrollere denne påstand bliver 100
roser af den nye stamme udsat for meldugssmitte. Det viser sig, at 12 roser bliver angrebet.
1) Bekræfter dette resultat rosengartnerens påstand? (Husk altid at anføre: Hvad X er.
Antagelser. Nulhypotese. Beregninger. Konklusion.).
2) Angiv et estimat ~ p for den nye stammes p.
3) Angiv et 95% konfidensinterval for den nye stammes p.
108

109
Opgaver til kapitel 9
Opgave 9.13
En fabrikant af chip til computere reklamerer med, at højst 2% af en bestemt type chip, som
fabrikken sender ud på markedet er defekte.
Et stort computerfirma vil købe et meget stort parti af disse chip, hvis påstanden er rigtigt. For
at teste påstanden købes 1000 af dem. Det viser sig, at 33 ud af de 1000 er defekte.
Kan fabrikantens påstand på denne baggrund forkastes på signifikansniveau 5% ?
Opgave 9.14
En producent af billigt plastiklegetøj får mange klager over at en bestemt type legetøj er
defekt ved salget. Legetøjet sælges til butikkerne i kasser på 10 stk, og som et led i en
kvalitetetskontrol udtages 100 kasser og antallet x af defekt legetøj optaltes. Følgende
resultater fandtes:
x 0 1 2 3 4 5 6
Antal kasser 34 38 19 6 2 0 1
Lad p være sandsynligheden for at få et defekt stykke legetøj.
1) Find et estimat ~ p for p.
2) Angiv et 95% konfidensinterval for p.
Opgave 9.15
Af 1000 tilfældigt udvalgte patienter, der led af lungekræft, var 823 døde senest 5 år efter
sygdommen blev opdaget.
Angiv på dette grundlag et 95% konfidensinterval for sandsynligheden for at dø af denne
sygdom senest 5 år efter at sygdommen bliver opdaget.
Opgave 9.16
En fabrikant af lommeregnere vurderer, at ca. 1% af de producerede lommeregnere er defekte.
For at få en nøjere vurdering heraf ønskes udtaget en stikprøve, der er så stor, at radius i et
95% konfidensinterval for fejlprocenten p er højst 0.5%.
Find stikprøvens størrelse n.
Opgave 9.17
Ved et køb af 100000 plastikbægre aftaltes med leverandøren, at det skal være en
forudsætning for købet, at partiet godkendes ved en stikprøvekontrol.
Kontrollen udøves ved, at 100 bægre udtages tilfældigt af partiet og kontrolleres. Partiet
godkendes, såfremt ingen af de 100 bægre er defekte.
Beregn sandsynligheden for, at partiet godkendes, hvis det i alt indeholder 250 defekte bægre.
Opgave 9.18
En fabrikant får halvfabrikata hjem i partier på 200000 enheder. Fra hvert parti udtages en
stikprøve på 100 enheder og antallet af fejlagtige blandt disse noteres.
Hvis dette antal er mindre end eller lig med 2, accepteres hele partiet; i modsat fald
undersøges partiet yderligere.
1) Hvad er sandsynligheden for, at et parti med en fejlprocent på 1 vil blive yderligere
undersøgt.
2) Hvor stor er sandsynligheden for, at et parti med en fejlprocent på 5 vil blive accepteret.

Vigtige diskrete fordelinger
Opgave 9.19
En maskinfabrikant påtænker at købe 100000 møtrikker af en bestemt type. Man beslutter sig
til at købe et tilbudt parti af den nævnte størrelse, såfremt en stikprøve på 150 møtrikker højst
indeholder 4% defekte møtrikker.
1) Beregn sandsynligheden for, at partiet bliver godkendt af maskinfabrikken, såfremt det
indeholder
a) 4% defekte møtrikker,
b) 2,5% defekte møtrikker,
c) 7,5% defekte møtrikker,
2) Bestem, for hvilken procentdel defekte møtrikker det ovennævnte parti (approksimativt)
har 50% sandsynlighed for at blive godkendt af maskinfabrikken.
Opgave 9.20
På en fabrik fremstilles gulvtæpper, som har størrelsen 20 m 2 . Ved fabrikationen er der
gennemsnitlig 6 vævefejl p. 100 m 2 klæde.
1) Beregn sandsynligheden for, at et tilfældigt gulvtæppe ingen vævefejl har.
2) Beregn sandsynligheden for, at et tilfældigt gulvtæppe højst har 2 vævefejl.
Fabrikken køber en ny væv. For at få et estimat for middelværdien måltes antallet af vævefejl
i 12 gulvtæpper hver på 20 m 2 . Resultaterne var
Gulvtæppe nr 1 2 3 4 5 6 7 8 9 10 11 12
Antal vævefejl 4 2 7 3 4 5 5 8 1 1 3 5
3) Find et estimat for middelværdien af antal vævefejl p. 20 m 2 klæde.
Opgave 9.21
Et radioaktivt præparat undergår gennemsnitligt 100 desintegrationer (sønderdelinger) p.
minut. Lad X betegne antal desintegrationer i et sekund (som er lille i forhold til præparatets
halveringstid).
Find P( X ≤ 1)
.
Opgave 9.22
Ved en TV-fabrikation optælles som led i en godkendelseskontrol antal loddefejl p. 5 TVapparater.
Fabrikanten ønsker at få et overblik over antal loddefejl, og optalte derfor antal
loddefejl på 24 tilfældigt udtagne TV apparater. Resultatet fremgår af skemaet:
Antal loddefejl 0 1 2 3 4 5 6 7 8 9
Antal TV apparater 3 2 4 6 5 2 1 0 1 0
Lad X være antallet af loddefejl i 5 TV apparater.
1) Angiv den sandsynlighedsfordeling X approksimativt kan antages at følge, og giv et
estimat for parameteren i fordelingen.
2) Beregn på basis af svaret i spørgsmål 1 sandsynligheden for, at der på 5 tilfældigt udtagne
TV-apparater højst er i alt 18 loddefejl?
110

111
Opgaver til kapitel 9
Opgave 9.23
På et teknisk universitet er et centralt edb-anlæg i konstant brug. Man har erfaring for, at
anlægget i løbet af en 20 ugers periode har gennemsnitligt 7 maskinstop.
Beregn sandsynligheden p for, at anlægget i en 4 ugers periode har mindst ét maskinstop.
Opgave 9.24
På en fabrik indtræffer i gennemsnit 72 ulykker om året. Antag, at de forskellige ulykker
indtræffer uafhængigt af hinanden, og at de er nogenlunde jævnt fordelt over året.
Beregn, idet et arbejdsår sættes lig med 48 uger, sandsynligheden for at der i en uge
indtræffer flere end 3 ulykker.
Opgave 9.25
Til et bestemt telefonnummer er der i løbet af aftenen i middel 300 opkald i timen.
Beregn sandsynligheden for, at der i løbet af et minut er højst 8 opkald.
Opgave 9.26
En fabrikation af fortinnede plader finder sted ved en kontinuerlig elektrolytisk proces.
Umiddelbart efter produktionen kontrolleres for pladefejl. Man har erfaring for, at der i
middel er 1 pladefejl hvert 5'te minut.
Beregn sandsynligheden for, at der højst er 5 pladefejl ved en halv times produktion.
Opgave 9.27
Lastbiler med affald ankommer tilfældigt og indbyrdes uafhængigt til en losseplads.
Lossepladsens maksimale kapacitet er beregnet til, at der i middel ankommer 90 lastbiler p.
time. Ledelsen af pladsen føler, at travlheden er blevet større i den sidste tid, således at
antallet af lastbiler overskrider den maksimale kapacitet. For at undersøge dette, foretages en
optælling af lastbiler i perioder à 10 minutter. Følgende resultater fremkom:
13 16 17 15 18 12 22 16 21 18
1) Bekræfter disse resultater ledelsens formodning? (Husk altid at anføre: Hvad X er.
Antagelser. Nulhypotese. Beregninger. Konklusion.).
2) Angiv et estimat ~µ for middelværdien µ [lastbiler/time].
3) Angiv et 95% konfidensinterval for middelværdien µ [lastbiler/time].
Opgave 9.28
Nedenstående tabel viser fordelingen af 400 volumenenheder med hensyn til antal gærceller
p. volumenenhed.
Antal gærceller 0 1 2 3 4 5 6 7 8 9 10 11 12
Antal volumenenheder 0 20 43 53 86 70 54 37 18 10 5 2 2
Lad X være antal gærceller p. volumenenhed. Det antages, at X er en stokastisk variabel der er
Poissonfordelt p ( µ ).
1) Find et estimat ~µ for µ .
2) Angiv et 95% konfidensinterval for µ .
3) Forudsat at X er Poissonfordelt p ( ~µ ) ønskes beregnet det forventede antal
volumenenheder, hvori der forekommer 5 gærceller (for x = 5).

Vigtige diskrete fordelinger
Opgave 9.29
Ved inspektion af en produktion med isolering af kobberledning taltes der i løbet af 50
minutter i alt 11 isoleringsfejl.
Idet antallet af isoleringsfejl p. 50 minutter antages at være Poissonfordelt p ( µ 1 ), skal man
1a) angive et estimat for .
µ 1
µ 1
1b) angive et 95% konfidensinterval for .
Det oplyses nu, at man i hver 5 minutters periode i den ovenfor omtalte 50 minutters periode
havde observeret følgende antal isoleringsfejl:
Periode 1 2 3 4 5 6 7 8 9 10
Antal fejl 1 0 2 2 1 1 3 0 1 0
Idet antallet af isoleringsfejl p. 5 minutter antages at være Poissonfordelt p ( ), skal man
2a)
2b)
angive et estimat for µ 2 .
angive et 95% konfidensinterval for .
µ 2
Opgave 9.30
I en urne findes 10 røde kugler, 5 hvide kugler og 3 sorte kugler.6 gange efter hinanden optages tilfældigt en kugle fra urnen.
Bestem sandsynligheden for, at der i alt er optaget 1 rød, 2 hvide og 3 sorte kugler, når
1) kuglerne optages uden tilbagelægning
2) kuglerne optages med tilbagelægning.
Opgave 9.31
En virksomhed fabrikerer farvede glasklodser til dekorationsbrug. Defekte glasklodser frasorteres. Man har erfaring for, at af
de frasorterede klodser har i middel 50% kun revner, 35% kun farvefejl, medens resten har begge disse fejl.
Beregn sandsynligheden for, at af 12 tilfældige defekte klodser har 6 kun revner, 4 kun farvefejl og 2 begge disse fejl.
Opgave 9.32
I et kortspil med de sædvanlige 52 spillekort har en spiller modtaget 13 kort. Angiv i procent med 2 decimaler
sandsynligheden for, at 3 af disse er esser og 5 er billedkort.
112
µ 2

113
10.2 Den rektangulære fordeling
10 ANDRE KONTINUERTE FORDELINGER
10.1 INDLEDNING
Vi vil i dette kapitel kort orientere om en række fordelinger, som er vigtige i specielle
sammenhænge,
10.2 DEN REKTANGULÆRE FORDELING
DEFINITION af rektangulær fordeling med parametrene a og b.
Lad a og b være to reelle tal, hvor a

Eksempel 10.1 Kontinuert variabel.
Lad randen af en roulette være ækvidistant inddelt efter en
skala fra 0 til 12, jævnfør figuren.
Ved et roulettespil bringes roulettens viser til at rotere,
hvorefter den standser ud for et tilfældigt punkt på skalaen.
Lad X være det tal som roulettens viser peger på.
Idet X må kunne antage ethvert tal mellem 0 og 12, må X
være en kontinuert variabel.
Angiv tæthedsfunktion og fordelingsfunktion for X og
skitser disse.
LØSNING:
x
Da P( 0 ≤ X ≤ x)
= for 0≤ x ≤12
12
er fordelingsfunktionen for X
⎧0
for x ≤ 0
⎪ x
F( x)=
⎨ for 0≤ x ≤12
⎪12
⎪
⎩1
for x ≥ 12
Ved differentiation fås tæthedsfunktionen
⎧ 1
⎪ for 0≤ x ≤12
f ( x)=
⎨12
⎪
⎩0
ellers
114

10.3 EKSPONENTIALFORDELINGEN
115
10.3 Eksponentialfordelingen
I kapitel 7 betragtede vi antallet N af revner pr. meter langs et kobberkabel. Vi antog, at N var
Poissonfordelt. Hvis vi i stedet havde betragtet afstanden X mellem revnerne, havde vi fået en ny
stokastisk variabel, som må være kontinuert. Som det fremgår af følgende sætning er X
eksponentialfordelt.
SÆTNING 10.2 (Eksponentialfordeling).
Lad W være en Poissonfordelt stokastisk variabel.
Lad det gennemsnitlige antal impulser i en tidsenhed være λ . Lad X være tiden indtil
næste impuls.
X er da en kontinuert stokastisk variabel med sandsynlighedsfordelingen
(tæthedsfunktionen)
f ( x ) = P ( X = x) bestemt ved
x ⎧ 1 −
µ
⎪ ⋅ e for x>
0
f ( x)=
⎨ µ
⎪
⎩0
ellers
hvor
Bevis:
I tidsrummet fra x0 til x0 + x er der I gennemsnit λ ⋅ x impulser. Lad W være det aktuelle antal impulser i tidsrummet
[x0 ; x0 + x ]. W er da Poissonfordelt p( λ ⋅ x)
.
Idet X er tiden fra én impuls til den næste, er P( X > x) = P( W = 0)
, da der ingen impulser er i tidsrummet
[x0 ; x0 + x ].
0
( λ ⋅ x) −λ⋅x −λ⋅x − ⋅x
Da PW ( = 0)
= ⋅ e = e , er P( X > x)
= e .
0!
λ
− ⋅x
Vi har derfor F( x) = P( X ≤ x) = 1− P( X > x)
= 1−e . λ
−λ⋅x Ved differentiation fås tæthedsfunktionen: f ( x) = F'( x)
= λ ⋅e. Sættes λ = fås formlen.
µ
1
Bevis for middelværdi og spredning:
∞
∞
−λ⋅x ⎡ −λ⋅x 1 ⎤ 1
E( X) = ∫ λ ⋅x⋅ e dx = -e ( x−
= = µ
0
⎣⎢
− λ⎦⎥ λ
∞
2 2 ⎡ ⎛
⎞ ⎤
2 −λ⋅x 2
V( X) = E( X ) − ( E( X) ) = ∫ λ ⋅x ⋅e dx − µ = ⎜ − + ⎟
0
⎢
⎣ ⎝
⎠ ⎥
⎦
−
− ⋅
-e λ x 2 2x2 x
2
λ λ
0
µ =
λ
1
X siges at være eksponentialfordelt exp ( µ ) med parameteren µ
.
∞
0
2 2
2
2 2
µ = − µ = µ .
λ
Som det fremgår af beviset for sætning 10.2, er fordelingsfunktionen for en eksponentialfordelt
variabel bestemt ved udtrykket
x
⎧ −
⎪ µ
F( x) = P( X ≤ x)
=
1− e for x > 0
⎨
⎩
⎪0
ellers

Andre kontinuerte fordelinger
På nedenstående graf er afbildet tæthedsfunktionen for eksponentialfordelingerne exp(1.0) og
exp(2.0)
1
0,8
0,6
0,4
0,2
0
0 2 4 6 8 10 12
Fig 10.1 Eksponentialfordelingerne exp(1) og exp(2)
Eksempel 10.2. Afstanden mellem successive revner i kabel.
Vi betragter det i eksempel 5.1 omtalte problem, hvor man fandt, at antallet N af mikroskopiske
revner i et kobberkabel er Poissonfordelt. Der var i gennemsnit 12.3 af den type revner pr. 10
meter. Lad X være afstanden mellem to på hinanden følgende revner.
Beregn sandsynligheden for, at der er mere end 1 meter mellem to revner.
LØSNING:
1
Da der i gennemsnit er 1.23 revner pr. meter, må der i gennemsnit være = 0812 . meter mellem
123 .
to revner. Vi har derfor at X er eksponentialfordelt med µ = 0.813.
1
⎛ − ⎞ 0813 .
−123
.
P( X > 1) = 1− P( X ≤ 1) = 1− ⎜1
− e ⎟ =e = 0. 2923
⎝ ⎠
Levetider. I apparater, som består af elektroniske komponenter (eksempelvis lommeregnere),
er der et meget ringe mekanisk slid. Apparatets fremtidige levetid vil derfor (næsten ikke)
afhænge af, hvor længe det har fungeret indtil nu. I sådanne tilfælde vil eksponentialfordelingen
erfaringsmæssigt være en god approksimativ model for apparatets levetid.
Det kan nemlig vises, at eksponentialfordelingen er den eneste kontinuerte fordeling, som har
ovennævnte egenskab (er uden hukommelse)
Bevis: Lad X være eksponentialfordelt med middelværdi µ og lad b > a > 0 være vilkårlige konstanter. Der gælder
da:
( ( > + ) ∧ ( > ) )
P X a b X a
P( X > a + bX > a)
=
P( X > a)
116
a b
− +
µ
P( X > a + b)
e
−
µ
=
= b =e = P( X > b)
P( X > a)
−
µ
e
b

1)
Γ ( x)
10.6 Den 2-dimensionale normalfordeling
Eksempel 10.3. Levetid for elektriske pærer.
Man har erfaring for, at en bestemt type elektriske pærer har en "brændtid" T (målt i timer), som
approksimativt er eksponentialfordelt. På basis af et stort antal målinger ved man , at
middellevetiden er µ = 1500 timer.
1) Hvor stor er sandsynligheden for, at en tilfældig pære brænder over, inden den har været tændt
i 1200 timer?
2) Find sandsynligheden for, at en tilfældig pære brænder i mere end 1800 timer.
3) En pære har brændt i 800 timer. Hvad er sandsynligheden for, at den brænder i mindst 1800
timer mere.
LØSNING:
1) PT ( < ) = F(
) = − . .
−
1200
1500
1200 1200 1 e = 1- 0.449 = 551%
1800
−
2) 1500
PT ( > 1800) = 1− F(
1800) = e = 3012% .
3) Da eksponentialfordelingen ingen hukommelse har, vil svaret blive som i spørgsmål 2, dvs.
30.12%.
10.4 WEIBULLFORDELINGEN
Hvis komponenterne i et elektronisk apparat ikke “slides”, dvs. den fremtidige levetid ikke
afhænger af den foregående tid, er som nævnt i afsnit 10.3 eksponentialfordelingen velegnet som
model for apparatets levetid.
Hvis derimod de pågældende komponenters eventuelle svigten afhænger af den forløbne tid, kan
man ofte med fordel benytte den i det følgende nævnte Weibullfordeling som approksimativ
model for apparatets levetid (model for apparatets pålidelighed).
DEFINITION af Weibulfordeling. Lad k og µ være positive tal. Sandsynlighedsfordelingen
for en kontinuert stokastisk variabel X med tæthedsfunktionen f ( x ) bestemt ved
x
k k
f x
x for x
k
ellers
k
⎧
−
⎪
−
( ) =
⋅ ⋅ >
⎨
⎪
⎩
⎛ ⎞
⎜ ⎟
1 ⎝ µ ⎠
e
0
µ
0
siges at være Weibullfordelingen wei( k,
µ
) .
⎛ k + 1⎞
µ E( X)
= µ ⋅Γ⎜
⎟
⎝ k ⎠
⎛ k + 2⎞⎛⎛k+ 1⎞⎞ Γ⎜⎟−⎜ ⎟
⎝ k ⎠
⎜ Γ
⎝ ⎝ k ⎠
⎟
⎠
2
Det kan vises, at Weibullfordelingen wei( k,
) har middelværdien
og spredningen σ ( X ) = µ ⋅
Det ses, at Weibullfordelingen kan opfattes som en generalisation af eksponentialfordelingen,
idet wei( 1 , µ ) = exp( µ ) .
Såfremt levetiderne for komponenter i et apparat aftager jo længere tid apparatet har været i
funktion (på grund af slid), kan man benytte en Weibullfordeling med k > 1 som approksimativ
model for apparatets levetid.
Gammafunktionen
grundbegreber” 3A
er defineret i “Supplement til statistiske
117
1 )

Andre kontinuerte fordelinger
10.5 DEN LOGARITMISKE NORMALFORDELING
Indenfor det biokemiske eller biologiske område (forsøgsdyrs reaktionstid, cellevækst m.v.) er
den stokastiske variabel X ikke normalfordelt, men hvis man foretager en logaritmisk
transformation Y = ln X er Y (approksimativt) normalfordelt.
Man siger så, at X er logaritmisk normalfordelt.
Tæthedsfunktionen for X er bestemt ved f x
for x > 0.
x e
2
1 ⎛ ln x−
µ ⎞
1 1 − ⋅⎜
⎟
2 ⎝ σ ⎠
( ) =
2π
⋅σ
Det kan vises, at mens Y = ln X har middelværdi µ og spredning σ har X middelværdi
µ 2
E( X) = e ⋅e
2µ
σ
og V( X)
= e ⋅e σ
⋅( e −1)
.
Nedenfor er tegnet en logaritmisk normalfordeling med middelværdi 8 og spredning 5.
density
1 2
− ⋅σ
0,15
0,12
0,09
0,06
0,03
0
Lognormal Distribution
0 10 20 30 40
x
2 2
118
Mean,Std. dev
8,5
10.6 DEN 2-DIMENSIONALE NORMALFORDELING
Flerdimensionale fordelinger vil blive omtalt nærmere i kapitel 9. Her nævnes uden forklaring
et eksempel herpå.
DEFINITION af 2-dimensional normalfordeling Lad µ 1, µ 2 være reelle tal og σ1, σ 2 være
positive tal. Sandsynlighedsfordelingen for 2-dimensional kontinuert stokastisk variabel (X1,X2) med tæthedsfunktion bestemt ved
1
−
⋅ −
⎛
2
2
⎛ x − ⎞ x − x − ⎛ x − ⎞ ⎞
⋅⎜
1 µ 1
⎜ ⎟ −2
1 µ 1⋅2
µ 2 + 2 µ
ρ
2
⎜ ⎟ ⎟
σ ⎝ ⎠ ⎟
2 σ 2 ⎠
1
f ( x) =
2π ⋅σ1⋅σ2 2
1−
ρ
2 ( 1
⋅ e
2
ρ ) ⎜
⎝ ⎝ σ1
⎠ σ1
kaldes den 2-dimensionale normalfordeling med
parametrene µ µ , og .
1, 2 σ 1 σ 2
Det kan vises, at E( X1)
= µ 1,
E( X2)
= µ 2,
σ( X 1) = σ1,
σ( X 2) = σ 2 og ρ( X1, X2
) = ρ
( defineres i kapitel 9).
Grafen ses overfor.

119
Opgaver til kapitel 10
OPGAVER
Opgave 10.1
På et betalingsnummer måltes man i tidsrummet fra kl 20 til 22 tiden t (antal minutter) mellem
på hinanden følgende telefonopkald. Følgende resultater fandtes:
Beliggenhed af t ]0;1] ]1;2] ]2;3] ]3;4] ]4;5] ]5;6] ]6;7] ]7;8] ]8;9] ]9;10] ]10; ∞ [
Antal observationer. 36 21 16 13 7 9 6 1 2 6 0
Det antages, at antallet N af telefonopkald til nummeret er Poissonfordelt. Lad T være tiden
mellem to opkald.
1) Angiv fordelingsfunktionen for T, og giv et estimat for middelværdien µ .
Vink: Antage, at for alle observationer i et interval er tidsrummet mellem observationerne
intervallets midterværdi.
2) På baggrund af den i spørgsmål 1 fundne estimat for µ , ønskes bestemt P( 2< T ≤3)
.
3) Af tabellen ses, at i intervallet ]2; 3] forekommer i alt 16 observationer. Angiv hvor mange
observationer man må forvente, ud fra resultatet i spørgsmål 2.
Opgave 10.2
Om en bestemt type elektriske komponenter vides, at deres levetider er eksponentialfordelte med
en middellevetid på 800 timer.
1) Find sandsynligheden for, at en komponent holder mindst 200 timer.
2) Find sandsynligheden for, at en komponent holder mellem 600 og 800 timer.
3) En komponent har holdt i 900 timer. Find sandsynligheden for, at den kan holde i mindst 200
timer mere.
4) I et elektrisk system indgår netop én komponent af denne type. Hver gang komponenten
svigter, udskiftes den øjeblikkeligt med en ny komponent af samme type. Find
sandsynligheden for, at komponenten udskiftes 12 gange i løbet af 8000 timer.
Opgave 10.3
Antag, at levetiderne for en bestemt slags elektroniske komponenter er uafhængige og alle er
eksponentialfordelt med en middellevetid på 3 (år). Betragt et delsystem bestående af 3 sådanne
komponenter i seriekobling:
(en seriekobling ophører at fungere, når én af komponenterne ophører at fungere).
Bestem middellevetiden for et sådant system.
Opgave 10.4
Nedbrydningstiden i den menneskelige organisme for et givet kvantum af et bestemt stof antages
at være eksponentialfordelt med middelværdien 5 timer.
Ved et forsøg indsprøjtes stoffet samtidig i 10 patienter.
1) Beregn sandsynligheden (afrundet til et helt antal procent) for, at stoffet hos en tilfældig valgt
patient vil være nedbrudt efter 8 timers forløb.
2) Beregn sandsynligheden for, at stoffet efter 8 timers forløb vil være nedbrudt hos mindst 5 af
patienterne.
3) Efter hvor mange timers forløb vil der være ca. 90% sandsynlighed for, at stoffet er nedbrudt
hos samtlige 10 patienter?
4) Hvor mange patienter skal indgå i en ny undersøgelse, hvis der skal være ca. 95%
sandsynlighed for, at der er mindst en patient, hvis organisme efter 8 timers forløb endnu ikke
har nedbrudt stoffet?

Bjarne Hellesen:
11 FLERDIMENSIONAL
STOKASTISK VARIABEL
ESSENS
Kovariansen V( Xi, X j) = E ( Xi − µ 1) ⋅( X2
− µ 2)
er et mål for to variables tendens til
at variere i takt med hinanden (samvarians). Kovariansen er f.eks. positiv(negativ), når afvigelsen
X i − µ i har en tendens til at være positivt (negativt) proportional med afvigelsen X j − µ j.
Er
X og X i j statistisk uafhængige, bliver kovariansen 0 (men man kan ikke slutte den anden vej).
V( Xi, X j)
Korrelationskoefficienten ρ(
Xi, X j)
≡
er normeret , så − 1≤ρ( Xi, X j)
≤ 1 .
σ ⋅σ
X2
95
85
75
65
55
45
150 160 170 180 190 200
X1
( )
X3
45
150 160 170 180 190 200
X1
Stikprøve viser positiv
Stikprøve viser ingen
korrelation: ρ( X1, X2)
≈ 084 . . korrelation: ρ( X , X ) = .
.
85
75
65
55
120
i j
1 2 000
X4
64
54
44
34
24
14
150 160 170 180 190 200
X1
Stikprøve viser negativ
korrelaton: ρ( X , X ) ≈− . .
1 2 084
2
Poolet estimat spool
=
2 2 2
fs 1 1+
fs 2 2 + ... + fs k k
med fpool f1 + f2+ ... + fk
= f1 + f2 + ... + fkfrihedsgrader
benyttes,
når man har k uafhængige estimater for den samme varians σ :
2
2 SAK1
2 SAK2
2 SAKk
s1
= , s2
= ,..., sk
= ,
f1
f 2
f k
2
Har to stikprøver givet estimaterne s1 2
= 2345 . , s2 = 3456 . med f1 = 6, f2
= 4 frihedsgrader,
2
bliver det poolede estimat spool
=
2
fs 1 1 +
f1 +
2
fs 2 2
=
f2
6 ⋅ 2. 345 + 4 ⋅3456
.
= 2. 7894 ≈ 2. 789
6+ 4
med f pool = f1 + f2
= 6+ 4 = 10
frihedsgrader.

121
11.1 Indledning
Linearitetsreglen E( a0 + a1X1 + a2X2+ ... + akXk) = a0 + a1E( X1) + a2E( X2) + ... + akE( Xk)
,
(a’erne er konstanter).
Er E( X1)
= 2 , E( X2)
= 3 fås
E( 4+ 5X + 6X ) = 4+ 5E( X ) + 6E( X ) = 4+ 5⋅ 2+ 6⋅ 3= 32.
1 2 1 2
Kvadratreglen V( a + a X + a X + ... + a X )
0 1 1 2 2
k k
2
2
2
= aV( X) + aV( X ) + ... + aV( X ) + 2 aaV( X, X )
1
1 2
2
k
∑
∑
k k i j i j
i=
1 j=+ i 1
Er V( X1) = 2, V( X2) = 3, V( X1, X2)
= 15 . , fås
2
2
V( 4 + 5X1 + 6X2) = 5 V( X1) + 6 V( X2) + 2⋅5⋅6⋅V( X1, X2)
2 2
= 5 ⋅ 2 + 6 ⋅ 3+ 2⋅5⋅6⋅ 15 . = 248
11.1 INDLEDNING
Ved anvendelserne optræder der ofte rflere
stokastiske variable X1, X2,..., Xkad gangen. Det kan da være
naturligt at samle dem i et ordnet sæt X = ( X1, X2,..., Xk) , som kaldes en k-dimensional stokastisk variabel.
Eksempelvis:
* Et levnedsmiddel kan af en tilfældig r udtaget forbruger bedømmes ved en karakter for smagen og en
karakter for lugten. Så er X = ( X , X ) = ( ) en 2-dimensional stokastisk variabel.
X 2
1 2 Smag,Lugt
* Et tilfældigt eksperiment r går ud på at udtage en tilfældig person og måle vedkommendes højde og masse
X 2 . Så er X = ( X , X ) = ( ) en 2-dimensional stokastisk variabel.
1 2 Højde, Masse
r
* Ugens 7 lottotal udgør en 7-dimensional stokastisk variabel X = ( X , X ,..., X ) .
1 2 7
r
* Et tilfældigt eksperiment går ud på at kaste en rød og en hvid terning. Så er X = ( X , X ) = (Antal øjne op
1 2
på rød terning, Antal øjne op på hvid terning) en 2-dimensional stokastisk variabel.
For hver af de 1-dimensionale stokastiske variable X1, X2,..., Xkhar vi tidligere defineret:
* Fordelingsfunktioner F1, F2,..., Fk: F( X ) ≡ P( X ≤ x ), F ( X ) ≡ P( X ≤ x ), . . . , F ( X ) ≡ P( X ≤ x ) .
1 1 1 1
2 2 2 2
k
k k k k
* Tæthedsfunktioner f1, f2,..., fk, når X X X er diskrete variable:
1, 2,...,
k
f ( x ) ≡ P( X = x ) , f ( x ) ≡ P( X = x ) , . . . , f ( x ) ≡ P( X = x ) ,
1 1 1 1
2 2 2 2
og når de er kontinuerte variable:
dF1( x1)
dF2( x2)
dFk( x k)
f1( x1)
≡ , f2( x2)
≡ , . . . , f k( xk)
≡ .
dx
dx
dx
1
2
k k k k
* Middelværdier, når X1, X2,..., Xker diskrete variable:
E( g( X ) ≡ g( x ) ⋅ f ( x ) , . . . , E( g( X ) ≡ g( x ) ⋅ f ( x ) ,
( )
∑ ( )
1 1 1 1
x1
∑
k
k k k k
xk og når de er kontinuerte variable:
E( g( X ) ≡
∞
g( x ) ⋅ f ( x ) dx , . . . , E( g( X ) ≡
∞
g( x ) ⋅ f ( x ) dx ,
( )
∫ ( )
1 1 1 1 1
−∞
∫
k k k k k
−∞
specielt
µ 1 ≡ E( X1) ≡ ∑ x1⋅ f1( x1)
, . . . , µ k ≡ E( X2) ≡ ∑ xk ⋅ fk( xk)
,
og
x1
xk
≡ E X ≡
∞
x ⋅ f x dx , . . . , ≡ E( X ) ≡
∞
x ⋅ f ( x )
dx .
∫
µ 1 ( 1) 1 1( 1) 1 µ k k k k k k
−∞
−∞
∫
.
X 1
X 1

Flerdimensional statistisk variabel
Af definitionen på middelværdi følger linearitetsreglen:
Ea ( ⋅ gX ( i) + bhX ⋅ ( i) ) = a⋅ EgX ( ( i) ) + bEhX ⋅ ( ( i)
) .
r
For en k-dimensional stokastisk variabel X = ( X X X definerer vi analogt:
1, 2,...,
k )
* Fordelingsfunktionen F : ( ∧ betyder “både og”)
F( x1, x2, ..., xk) ≡ P( X1 ≤ x1) ∧ P( X2 ≤ x2) ∧... ∧P( X k ≤ xk)
.
* Tæthedsfunktionen f, når X1, X2,..., X k er diskrete variable:
f ( x1, x2, ..., xk) ≡ P( X1 = x1) ∧ P( X2 = x2) ∧... ∧ P( X k = xk)
k
F( x1, x2,..., xk)
og når de er kontinuerte variable: f ( x1, x2, ..., xk)
≡ .
x1 x2,..., xk
∂
∂ ∂ ∂
* Middelværdier, når X1, X2,..., Xker diskrete variable:
E g( X , X ,..., X ) = ... g( x , x ,..., x ) ⋅ f ( x , x ,..., x )
( )
∑∑
∑
1 2 k 1 2 k 1 2
x1 x2
xk
og når de er kontinuerte variable:
( )
∫
∞
∞
∫ ∫
∞
EgX ( 1, X2,..., X k) = dx1 dx2... gx ( 1, x2,..., xk) ⋅ f( x1, x2,..., xk) dxk
−∞ −∞
−∞
r r r r
Af definitionen på middelværdi følger linearitetsreglen: Ea ( ⋅ gX ( ) + bhX ⋅ ( ) ) = a⋅ EgX ( ( ) ) + bEhX ⋅ ( ( ) )
De variable X1, X2,..., Xkkaldes stokastisk uafhængige, såfremt de for alle værdier af x1, x2,..., xkopfylder betingelsen: f ( x , x ..., x ) = f ( x ) ⋅ f ( x ) ⋅... ⋅ f ( x ) ,
1 2 k 1 1 2 2
k k
der kan vises at være ækvivalent med betingelsen: Fx ( , x..., x) = F( x) ⋅F( x) ⋅... ⋅F(
x)
.
122
k
1 2 k 1 1 2 2
k k
r
En rstikprøve r raf
størrelsen n på en stokastisk variabel X = ( X , X ,..., X defineres som
1 2 k )
( X1, X2,..., Xn) = ( ( X11, X21,..., Xk1),( X12, X22,..., Xk2),...,( X1n, X2n,..., Xkn)
r r r
) r
hvor X1, X2,..., Xner statistisk uafhængige variable, der hver har samme fordeling som X .
Eksempel 11.1. 2-dimensional stokastisk variabel.
Et levnedsmiddel kan af en tilfældig forbruger bedømmes ved en karakter for smagen og en karakter for
X 1
lugten. Karakteren kan antage værdierne 0, 1 og 2, mens kun kan antage værdierne 0 og 2.
a) Antag, at man teoretisk kender tæthedsfunktionen f ( x , x ) :
x 2
f ( x1, x2)
x1 1 2
X 2
X 1
0 1 2
0 0.2 0.1 0.1
2 0.1 0.2 0.3
a1) Find de 1-dimensionale tæthedsfunktioner f1( x1)
og f2( x2)
.
a2) Er X 1 og X 2 statistisk uafhængige ?
a3) Find middelværdierne µ 1 = E( X1)
og µ 2 = E( X2)
samt spredningerne σ1 = σ(
X1) og σ 2 = σ(
X 2)
.
a4) Find middelværdien E( X1, X2)
.
b) Antag, at man i stedet kender en stikprøve på ( X1, X2)
:
(1,2), (0,0), (2,2), (2,2), (1,0), (2,2), (0,2), (2,2), (0,2 ), (2,2).
b1) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a3).
LØSNING:
a1) Ved summation ned gennem de lodrette søjler i tabellen for tæthedsfunktionen
f ( x1, x2) ≡ P( X1 = x1 ∧ X2 = x2)
fås den 1-dimensionale tæthedsfunktion f1( x1) = P( X1 = x1)
:
f1( 0) = 02 . + 01 . = 03 . , f1() 1 = 01 . + 02 . = 03 . , f1( 2) = 01 . + 03 . = 04 . .
Ved summation hen gennem de vandrette rækker i tabellen for tæthedsfunktionen f ( x1, x2)
fås analogt den
1-dimensionale tæthedsfunktion f2( x2)
:
f 2( 0) 02 . 01 . 01 . 04 . , ( ) = . + . + . =
. .
= + + = f 2 2 01 02 03 06
X 2

123
11.1 Indledning
a2) De variable X 1 og X 2 er statistisk uafhængige, hvis og kun hvis f ( x1, x2) = f1( x1) ⋅ f2( x2)
for alle
værdier af ( x1, x2)
i definitionsmængden. Men da f.eks. f1( 0) ⋅ f2(
0) = 03 . ⋅ 04 . = 012 . er forskellig fra
f (,) 00 02 . , er og ikke statistisk uafhængige.
= X 1 X 2
a3) Vi finder
µ 1 = E( X1) = ∑ x1 ⋅ f1( x1) = 0⋅ f1( 0) + 1⋅ f1( 1) + 2⋅ f1(
2)
= 003 ⋅ . + 103 ⋅ . + 204 ⋅ . = 11 .
= E( X ) = x ⋅ f ( x ) = 0⋅ f ( 0) + 2⋅ f ( 2) = 0⋅ 04 . + 2⋅ 06 . = 12 .
∑
µ 2 2 2 2 2 2 2
2 ( )
2
σ = σ ( X ) ≡ V( X ) ≡ E ( X − µ ) = ( x − µ ) ⋅ f ( x )
1 1 1 1 1
∑
1 1
2 2 2
= ( 0 −11 . ) ⋅ 0. 3 + ( 1−11 . ) ⋅ 0. 3 + ( 2 −11 . ) ⋅ 0. 4 = 0. 69 = 083067 .
2 ( )
1 1
2
σ = σ ( X ) ≡ V( X ) ≡ E ( X − µ ) = ( x − µ ) ⋅ f ( x )
2 2 2 2 2
∑
2 2
2 2
=
2 2
( 0 −12 . ) ⋅ 0. 4 + ( 2 −12 . ) ⋅ 0. 6 = 0. 96 = 0. 97980
a4) Vi finder
E( X1 ⋅ X2) ≡ ∑ ∑ x1 ⋅ x2 ⋅ f ( x1, x2)
= 00 ⋅ ⋅ f ( 00 , ) + 10 ⋅ ⋅ f ( 10 , ) +
x1
x2
2⋅0⋅ f (,) 20 + 0⋅2⋅ f (,) 02 + 1⋅2⋅ f (,) 12 + 2⋅ 2⋅ f (,) 22
= 0⋅ 02 . + 0⋅ 01 . + 0⋅ 01 . + 0⋅ 01 . + 2⋅ 02 . + 4⋅ 03 . = 16 . .
b1) Stikprøvens x1 -værdier 1, 0, 2, 2, 1, 2, 0, 2, 0, 2 kan indtastes på en lommeregner, der finder gennemsnittet
x1 og standardafvigelsen s1 som tilnærmelser til middelværdi µ 1 og spredning σ1 for X 1 . Man finder:
µ 1 ≡ E( X1) ≈ x1=
12 . , σ1 = σ(
X1) ≈ s1
= 09189 . .
x 2
Analogt indtastes stikprøvens - værdier 2, 0, 2, 2, 0, 2, 2, 2, 2, 2, og man finder
µ 2 ≡ E( X2) ≈ x2=
16 . , σ = σ(
X ) ≈ s = .
2 2 2 08433
Det ses, at estimaterne har en vis lighed med de eksakte værdier i spørgsmål a3).
11.2 KOVARIANS OG KORRELATIONSKOEFFICIENT
Vi har omtalt, at hver stokastisk variabel har en varians. Men et par variable og kan have en tendens til at
variere i overensstemmelse med hinanden (samvarians), således at afvigelserne X1 − µ 1 og X 2 − µ 2 overvejende
har samme fortegn (positiv korrelation) eller overvejende har modsat fortegn (negativ korrelation). Eksempelvis kan
en høj forekomst af ét vitamin i et levnedsmiddel ofte være ledsaget af en høj forekomst af et andet vitamin (positiv
korrelation).
Og studerendes højde og masse kan også have en positiv rkorrelation.
Vi betragter igen en k-dimensional stokastisk variabel X = ( X X X . For et par af variable og
1, 2,..., k )
X X i j
defineres kovariansen (“samvariansen”)
( µ µ )
V( X , X ) ≡ E ( X − ) ⋅( X − )
i j i i j j
(den giver jo et vist mål for, om afvigelserne X i − µ og X i
j − µ j i middel har samme fortegn eller modsat
fortegn).
Sættes i = j, fås V( Xi, Xi) = E( ( Xi
− µ i)
) , som er identisk med variansen for variablen
2
V( Xi) X i
( )
2 2
Man kan vise (se nedenfor), at V( Xi, X j) = E Xi ⋅X j − i ⋅ j,
som for i = j giver V( X ) = E X − µ .
X 1
X 2
µ µ ( )
i i i
Bevis:
V( Xi, X j) ≡ E( ( Xi − µ i) ⋅( X j − µ j) ) = E( XiX j − µ iX j −
Anvendes linearitetsreglen kan sidste led omformes:
Xiµ
j + µ iµ j)
.
= E( X X ) − µ E( X ) − E( X ) µ + µ µ = E( X X ) − µ µ − µ µ + µ µ = E( X X ) − µµ
i j i j i j i j i j i j i j i j
i j i j

Flerdimensional stokastisk variabel
For bedre at kunne vurdere hvor meget de variable varierer i “takt” med hinanden, divideres kovariansen med
spredningerne, så man får den såkaldte korrelationskoefficient:
V( Xi, X j)
ρ(
Xi, X j)
≡
σ ⋅ σ
1 2
Man kan vise (se nedenfor) , at −1≤ ρ( Xi, X j)
≤ 1.
Bevis: Vi har
2
0 ≤ E
⎛⎜
⎝ ( λ ⋅ X − + X −
⎞ ) ⎟
i µ i j µ j ⎠ = E λ ⋅( Xi − µ i) + 2λ
( Xi − µ i)( X j − µ j) + ( X j − µ j)
2 2 2
( ) ( ) ( )
2
( ( i i) ) 2 ( ( i i)( j j) ) ( ( j j)
) = λ ⋅ V Xi + 2V
Xi X j λ + V X j
= λ ⋅ E X − µ + λ E X − µ X − µ + E X − µ
2 2 2
λ
124
( ) ( , ) ( )
Da dette andengradspolynomium i aldrig er negativt, kan diskriminanten ikke være positiv, dvs.
( )
2
V( Xi, X j)
2
4( V( Xi, X j) ) −4⋅V( Xi) ⋅V( X j)
≤0⇔ ≤1⇔ ( ρ( Xi, X j)
) ≤1
⇔−1≤ρ( Xi, X j)
≤1
.
V( X ) ⋅V(
X )
i j
Man kan (som det ses nedenfor) vise, at
X 1 og X 2 stat. uafhængige ⇒ E( X ⋅ X ) = E( X ) ⋅ E( X ) ⇔ V( X , X ) = 0 ⇔ ρ(
X , X ) = 0
Bevis: Vi har
og stat. uafhængige
X 1 X 2 ⇔ f xi x j = fi xi ⋅ f j x j
2
i j i j i j i j
( , ) ( ) ( )
∑∑ ∑∑
⇒ E( X ⋅ X ) = x ⋅x ⋅ f ( x , x ) = x ⋅x ⋅ f ( x ) ⋅ f ( x )
∑
i j i j i j
xi
x j
xi
x j
∑
i j i i j j
= xi ⋅ fi( xi) xj ⋅ f j( xj) = E( Xi) ⋅E(
X j)
xi x j
⇔ V( Xi, X j) = E( Xi ⋅ X j) − µ i ⋅ µ j =
V( Xi, X j)
E( Xi) ⋅ E( X j) − µ i ⋅ µ j = 0 ⇔ ρ(
Xi, X j)
=
= 0.
σ ⋅ σ
Estimater for kovarians, varians og korrelationskoefficient
Ud fra en stikprøve ( x1, y1),( x2, y2), ...,( xn, yn)
kan man beregne
SAPXY n
≡ ∑ ( xi − x) ⋅( yi − y)
,
n
2
SAKX ≡ ∑ ( xi − x)
,
n
SAKX ≡ ∑ ( xi − x)
i=
1
( SAP = “Sum af Afvigelsers Produkter” , SAK = “Sum af Afvigelsers Kvadrater” )
og heraf danne estimater for kovarians, varianser og korrelationskoefficient:
SAPXY
SAK X SAKY
kovarians: V( X, Y)
≈ og varianser: V( X)≈
, VY ( )≈
n − 1
n − 1 n − 1
korrelationskoefficient: ρ( XY , ) ≈r≡ i=
1
SAPXY
SAK ⋅ SAK
X Y
Det kan således vises (for enhver fordelingstype), at
E , ,
SAP ⎛ XY ⎞
⎜ ⎟ = V( X, Y)
⎝ n − 1 ⎠
E SAK ⎛ X ⎞
⎜ ⎟ = V( X)
⎝ n − 1 ⎠
E SAK ⎛ Y ⎞
⎜ ⎟ = VY ( )
⎝ n − 1 ⎠
i=
1
2
i j

Bevis: Vi har
n
n
∑ ( )( ) ∑ ( ( i µ x) ( µ x) ( ( i µ Y) ( µ Y)
)
SAP = X − X Y − Y = X − − X − ⋅ Y − − Y −
XY i i
i=
1 i=
1
n
n
∑ ∑
∑ ∑
= ( X − µ )( Y − µ ) + ( X − µ )( Y − µ ) − ( X − µ )( Y − µ ) − ( X − µ )( Y − µ )
i x i Y
x Y i x Y
x i Y
i=
1 i=
1
i=
1 i=
1
n
∑ ( Xi i=
1
n
µ x)( Yi µ Y)
n ( X µ x)( Y µ Y) ( nX n µ x)( Y µ Y) ( X µ x)( nY n µ Y)
= − − + ⋅ − − − − ⋅ − − − − ⋅
= ∑ ( Xi − µ x)( Yi − µ Y)
− n⋅( X − µ x)( Y − µ Y)
.
i=
1
Altså fås ved hjælp af linearitetsreglen:
n
E( SAPXY ) = ∑ E ( Xi− µ x )( Yi− µ Y ) − n⋅E ( X − µ x )( Y − µ Y )
i=
1
( ) ( )
n
1
= ∑ V( Xi, Yi)
− ⋅ E ( X1 + X2+ ... + Xn − n⋅ i=
1 n
x)( Y1 + Y2+ ... + Yn − n⋅
Y)
n
⎛ n
n
1
⎞
= ∑V( X, Y)
− ⋅E⎜∑( Xi− µ x) ∑(
Yj
− µ Y ) ⎟
i=
1 n ⎝ i=
1 j=
1 ⎠
n
( µ µ )
n n
n n
1 1
= nV ⋅ ( XY , ) − ∑∑
E( ( Xi − µ x)( Yj − µ Y) = n⋅V( X, Y)
− ∑∑V(
Xi, Yj)
n
n
i=
1 j=
1
n
1
= nV ⋅ ( XY , ) − ∑V(
Xi, Yi)
n
i=
1
125
i=
1 j=
1
( idet V( X , Y )= 0 for i ≠ j i en stikprøve)
i j
n
11.1 Indledning
1
= nV ⋅ ( XY , ) − ⋅nV ⋅ ( XY , ) = ( n−1) ⋅V(
XY , ) , dvs. E .
n SAP ⎛ XY ⎞
⎜ ⎟ = V( X, Y)
⎝ n − 1 ⎠
Erstattes Y med X i beviset, bliver SAPXY erstattet med SAK X , og V( X, Y)
bliver erstattet med V( X)
,
hvorved vi også får bevist, at E . Erstattes X med Y , fås endelig
SAK ⎛ X ⎞
⎜ ⎟ = V( X)
E
⎝ n − 1 ⎠
SAK ⎛ Y ⎞
⎜ ⎟ = VY ( )
⎝ n − 1 ⎠
Poolet estimat
Som nævnt er SAK en forkortelse for “Sum af Afvigelsers Kvadrater”. De afvigelser der tænkes på er de n differenser
X1 − X, X2 − X,..., Xn− X . De har summen 0, så når n - 1 af dem er kendt, er den sidste fastlagt. Da SAK således
kun er baseret på n - 1 uafhængige differenser, siger man, at SAK har f = n - 1 frihedsgrader. Det er også antallet
2 SAKX
af frihedsgrader der optræder i estimatet for varians: s =
f
Ofte har man taget k stikprøver på variable med samme varians σ , så vi får k uafhængige estimater for den samme
2
varians σ : 2
2 SAK1
2 SAK2
2 SAKk
s1
= , s2
= ,. . . . . ., sk
=
f1
f 2
f k
og det er da fordelagtigt at forene dem i et såkaldt fællesestimat eller poolet estimat:
2
spool
=
2 2 2
fs 1 1+
fs 2 2+
... + fs k k
f1 + f2 + ... + fk
med f pool = f1 + f2+ ... + fkfrihedsgrader
.
Dette kan også skrives
2 SAK1 + SAK2+ ... + SAKk
spool
=
, med fpool =
f1 + f2+ ... + fk
f1 + f2 + ... + fkfrihedsgrader.
2
Det ses, at spool har den rigtige middelværdi σ , idet linearitetsreglen giver
2
2
Es ( pool ) =
2
2 2
fEs 1 ( 1)
+ fEs 2 ( 2)
+ ... + fkEs ( k)
=
f + f + ... + f
2 2 2
f1σ + f2σ + ... + fkσ
2
= σ
.
f + f + ... + f
1 2
k
1 2
k

Flerdimensional stokastisk variabel
Eksempel 11.2. Kovarians. Korrelationskoefficient.
Vi betragter igen den 2-dimensionale fordeling fra eksempel 11.1.
a5) Find kovariansen og korrelationskoefficienten.
b2) Benyt stikprøven til at finde estimater for kovariansen og korrelationskoefficienten.
LØSNING:
a5) Idet vi i eksempel 11.1 har fundet µ 1 = 11 .,µ 2 = 12 . , σ = 069 . og σ = 096 . , finder vi nu kovariansen
V( X1, X2)
og korrelationskoefficienten ρ( X1, X2)
:
( )
V( X , X ) ≡ E ( X − µ ) ⋅( X − µ ) = ( x − µ )( x − µ ) f ( x , x )
i j i i j j
∑∑
x1
x2
1 1 2 2 1 2
= ( 0− µ 1) ⋅( 0− µ 2) ⋅ f ( 00 , ) + ( 1− µ 1) ⋅( 0− µ 2) ⋅ f ( 10 , ) + ( 2−µ 1) ⋅ ( 0−µ 2)
⋅ f ( 20 , )
+ ( 0− µ 1) ⋅( 2 − µ 2) ⋅ f ( 02 , ) + ( 1− µ 1) ⋅( 2 − µ 2) ⋅ f ( 12 , ) + ( 2 − µ 1) ⋅ ( 2 − µ 2)
⋅ f ( 22 , )
= ( 0−11 . ) ⋅( 0−1.. 2) ⋅ 02 . + ( 1−11 . ) ⋅( 0− 12 . ) ⋅ 01 . + ( 2− 11 . ) ⋅ ( 0− 12 . ) ⋅ 01 .
+ ( 0− 11 . ) ⋅( 2 − 1.. 2) ⋅ 01 . + ( 1− 11 . ) ⋅( 2 − 12 . ) ⋅ 02 . + ( 2 − 11 . ) ⋅ ( 2 − 12 . ) ⋅ 03 . = 028 .
V( X1, X2)
028 .
ρ(
X1, X2)
≡
=
= 0. 3440 .
σ( X ) ⋅σ(
X ) 069 . ⋅ 096 .
1 2
b2) Stikprøvens værdier (1,2), (0,0), (2,2), (2,2), (1,0), (2,2), (0,2), (2,2), (0,2), (2,2) kan indtastes på en
lommeregner, der finder tilnærmelser (estimater) til kovariansen V( X1, X2)
og korrelationskoefficienten
ρ( X , X ) :
1 2
n
∑
( x1i − x1)( x2i − x2)
SAP12
i=
1
V( X1, X2)
≈ =
= 03111 .
n − 1 n − 1
ρ( X , X ) ≈ r ≡
1 2
SAP12
SAK ⋅ SAK
1 2
=
i=
1
n
∑
i=
1
n
∑
( x − x )( x − x )
1i 1 2i 2
( x − x ) ⋅ ( x − x )
n
∑
1i 1 j
j
2
2 2 2
= 1
126
= 04015 .
Det ses, at estimaterne har en vis lighed med de eksakte værdier i spørgsmål a5).
11.3 LINEARKOMBINATION
Når vi skal tage en stikprøve ( X1, X2,..., Xn) på en 1-dimensional stokastisk variabel X, så skal vi n gange skaffe
et r tal X fra et tilfældigt eksperiment. Derfor kan vi opfatte stikprøven som en n-dimensional stokastisk variabel
X = ( X X X .
1, 2,...,
n )
X X X
Vi bruger ofte stikprøven til at danne gennemsnittet X
n n X
n X
n X
1 + 2+
... + n 1 1 1
=
= 1 + 2+
... + n
som er en speciel linearkombination af X1, X2,..., Xn. r
Ved en linearkombination L for en k-dimensional stokastisk variabel X = ( X X X forstås et udtryk af
1, 2,...,
k )
formen
L = a0 + a1X1 + a2X2 + ... + akXk , hvor a0, a2, a3,..., aker konstanter.
For middelværdien af L giver linearitetsreglen:
E( L) = a0 + a1E( X1) + a2E( X2) + ... + akE( Xk)
.
Eksempelvis kan vi se, at et gennemsnit X altid har den “rigtige” middelværdi µ :
1 1 1 1 1 1
E( X)
= E( X1)
+ E( X2
) + ... + E( Xn)
= µ + µ + ... + µ = µ .
n n n n n n
For variansen af en linearkombination L gælder kvadratreglen:
2
2
2
V( L) = a ⋅ V( X ) + a ⋅ V( X ) + ... + a ⋅ V( X ) + 2
a a V( X , X )
1
1 2
2
k
k k i j i j
i=
1 j=+ i 1
k
∑ ∑
.

127
11.3 Linearkombination
Eksempelvis:
2 2
a) V( a + bX + cY) = b V( X) + c V( Y) + 2bcV(
X, Y)
b) V( a + bX + cY + dZ)
2 2 2
= b V ( X ) + c V ( Y) + d V ( Z) + 2bcV ( X , Y) + 2cdV( Y, Z) + 2dbV
( Z, X ) .
c) V X V X V X
(X’erne statistisk uafhængige)
n n n V X 1 1 1
( ) = 2 ( 1) + 2 ( 2) + ... + 2 ( n)
2
1 2 1 2 1 2 σ
σ(
X )
= + + + = , dvs. .
2 σ 2 σ ... 2 σ
σ(
X ) =
n n n n
n
Den sidste ligning viser, at spredningen på et gennemsnit kun er omvendt proportional med kvadratroden på
stikprøvestørrelsen n. For at få et gennemsnit med en 10 gange mindre spredning, skal stikprøven altså gøres 100 gange
større!
Bevis for kvadratreglen. Vi finder
( 2)
( 0 1 1 k k 0 1µ 1 kµ k
2)
( ( µ ) ... (
2
µ ) )
V( L) ≡ E ( L− E( L)) = E ( a + a X + ... + a X − a − a −... −a
)
( 1 1 1
k k k )
= E a X − + + a X −
⎛
k k
⎞
2
2 2 2
= E⎜a X − + + a X − + ∑ ∑ a a X − X − ⎟
1 ( 1 µ 1)
... k( k µ k) 2
i j( i µ i)( j µ j)
⎝
i=
1 j=
1
⎠
k k
2 2 2
( ( 1 µ 1)
) ... k ( ( k µ k) ) 2∑
∑ i j ( ( i µ i)( j µ j)
)
2
= a E X − + + a E X − + a a E X − X −
1
∑ ∑
i=
1 j=
1
2
2
= aV( X) + ... + aV( X ) + 2 aaV( X, X ).
1
1
k
k k i j i j
i=
1 j=
1
k
Eksempel 11.3. Linearkombination af stokastiske variable.
Et levnedsmiddel leveres i poser. Lad X 1 og X 2 [mg/kg] betegne koncentrationerne af to stoffer A og B i en
tilfældig udvalgt pose. Det vides, at E( X1)
= 20. 0,
E( X2)
= 30. 0 , σ( X 1)
= 20 . , σ( X 2 ) = 40 . og
V( X1, X2)
= −40 . . Holdbarheden Y er teoretisk givet ved Y = 5+ 4X1 + 3X2[dage]
.
Find holdbarhedens middelværdi EY ( ) og spredning σ( Y)
.
LØSNING:
Vi finder
EY ( ) = E( 5+ 4X1 + 3X2) = 5+ 4⋅ E( X1) + 3⋅E(
X2
) = 5 + 4 ⋅ 20. 0 + 3⋅ 30. 0 = 1750 .
2
2
VY ( ) = V( 5+ 4X1 + 3X2) = 4 ⋅ V( X1) + 3 ⋅ V( X2) + 243 ⋅ ⋅ ⋅V(
X1, X2)
2 2 2 2
= 4 ⋅ 20 . + 3 ⋅ 40 . + 2⋅4⋅3⋅( − 40 . ) = 112
σ( Y) ≡ V( Y)
= 112 = 105830
. .

Flerdimensional stokastisk variabel
OPGAVER
Opgave 11.1.1 (2-dimensional stokastisk variabel)
Et spil i et casino går ud på at trække en tilfældig seddel fra en urne (og lægge sedlen tilbage igen). Urnen indeholder
10 sedler, og på hver seddel står 2 tal ( X1, X2)
:
(1,0) (3,0) (4,0)
(1,0) (3,3) (4,3)
(1,3)
(1,3)
(1,3)
(4,3)
a1) Find den 2-dimensionale tæthedsfunktion f ( x1, x2)
:
a2) Find de 1-dimensionale tæthedsfunktioner f1( x1)
og f2( x2)
.
a3) Er X 1 og X 2 statistisk uafhængige ?
a4) Find middelværdierne µ 1 = E( X1)
og µ 2 = E( X2)
samt spredningerne σ1( X 1)
og σ 2( X 2)
.
2
a5) Find middelværdien E( X1⋅X2) .
b) Antag, at man i stedet kender en stikprøve på ( X1, X2)
:
(1,3), (1,0), (1,0), (4,3), (3,0), (4,3), (1,0), (3,0), (3,3 ), (1,3).
b1) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a4).
Opgave 11.1.2 (kovarians, korrelationskoefficient)
a6) Find kovariansen V( X1, X2)
og korrelationskoefficienten ρ( X1, X2)
.
b2) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a6).
Opgave 11.1.3 (linearkombination)
For det i opgave 11.1.1 og 11.1.2 omtalte casino aftales et spil, hvor gevinsten er
G = 20 + 10X1 + 5X2.
a7) Find gevinstens middelværdi E( G)
og spredning σ( G)
.
b3) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a7).
Opgave 11.2.1 (2-dimensional stokastisk variabel)
Under en produktion kan der optræde fejl. Lad ( X1, X2)
=( Antal gange der optræder fejl af type 1, Antal gange der
optræder fejl af type 2) i en tilfældig produktion. Variablen X 1 kan antage værdierne 0, 1 og 2, mens X 2 kun kan antage
værdierne 0 og 1.
a) Antag, at man teoretisk kender tæthedsfunktionen f ( x , x ) :
1 2
f ( x1, x2)
x1 0 1 2
x2 0 0.3 0.1 0.1
1 0.1 0.2 0.2
a1) Find de 1-dimensionale tæthedsfunktioner f1( x1)
og f2( x2)
.
a2) Er X 1 og X 2 statistisk uafhængige ?
a3) Find middelværdierne µ 1 = E( X1)
og µ 2 = E( X2)
samt spredningerne σ1( X 1)
og σ 2( X 2)
.
a4) Find middelværdien E( X1 + X2)
.
b) Antag, at man i stedet kender en stikprøve på ( X1, X2)
:
(0,1), (0,0), (1,1), (1,1), (0,0), (0,0), (0,1), (2,1), (0,0 ), (2,1).
b1) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a3).
Opgave 11.2.2 (kovarians, korrelationskoefficient)
Vi betragter igen produktionsprocessen fra opgave 11.2.1.
a5) Find kovariansen V( X1, X2)
og korrelationskoefficienten ρ( X1, X2)
.
b2) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a5).
128

Opgave 11.2.3 (linearkombination)
For den i opgave 11.2.1 og 11.2.2 omtalte produktionsproces er fortjenesten
F = 20000 − 3000X1 − 4000X2.
a6) Find fortjenestens middelværdi E( F)
og spredning σ( F)
.
b3) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a6).
129
Opgaver til kapitel 11
Opgave 11.3.1 (2-dimensional stokastisk variabel)
År 4001. En sonde er vendt hjem med oplysninger om individer på en fremmed planet. De kan have 2, 4 eller 6 øjne,
og 2 eller 4 ører. Lad ( X , X ) = (Antal øjne, Antal ører) for et tilfældigt udtaget individ på planeten.
1 2
a) Professor Cosmussen har teoretisk opstillet tæthedsfunktionen f ( x , x ) :
f ( x1, x2)
x 2
x 1
1 2
2 4 6
2 0.1 0.2 0.1
4 0.1 0.3 0.2
a1)
a2)
a3)
Find de 1-dimensionale tæthedsfunktioner f1( x1)
og f2( x2)
.
Er X 1 og X 2 statistisk uafhængige ?
Find middelværdierne µ 1 = E( X1)
og µ 2 = E( X2)
samt spredningerne σ1( X 1)
og σ 2( X 2)
.
⎛ 1
a4) Find middelværdien E⎜ ⎝ X
1 ⎞
+ ⎟ .
X ⎠
1 2
b) Antag, at man i stedet kender en stikprøve på ( X1, X2)
:
(6,2), (2,4), (6,4), (2,2), (6,4), (4,4), (2,2), (4,2), (4,4 ), (4,4).
b1) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a3).
Opgave 11.3.2 (kovarians, korrelationskoefficient)
Vi betragter igen individerne fra opgave 11.2.1.
a5) Find kovariansen V( X1, X2)
og korrelationskoefficienten ρ( X1, X2)
.
b2) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a5).
Opgave 11.3.3 (linearkombination)
For de i opgave 11.3.1 og 11.3.2 omtalte individer har professor Cosmussen opstillet en formel for deres masse:
M = 200 + 20X1 + 10X2
kg.
a6) Find massens middelværdi E( M)
og spredning σ( M)
.
b3) Benyt stikprøven til at finde estimater for størrelserne i spørgsmål a6).
Opgave 11.4.1 (2-dimensional stokastisk variabel)
Lad ( X1, X2)
= ( Højde [cm], Masse [kg] ) af en tilfældigt udtaget studerende på 3. halvår.
Der foreligger følgende stikprøve:
(178,63), (186,85), (180,68), (183,75), (164,55), (193,77),
(193,84), (160,55), (165,63), (180,84), (169,74), (189,79) .
Find estimater for middelværdierne = E X og = E X samt spredningerne ( ) og ( X ) .
µ 1 ( 1)
µ 2 ( 2)
σ1 X 1 σ 2 2
Opgave 11.4.2 (kovarians, korrelationskoefficient)
Benyt stikprøven i opgave 11.4.1 til at finde estimater for kovariansen V( X1, X2)
og korrelationskoefficienten
ρ( X , X ) .
1 2
Opgave 11.4.3 (linearkombination)
Vi betragter igen de i opgave 11.4.1 og 11.4.2 omtalte studerende. En frugtavler har opstillet en formel for den timeløn,
han vil give dem som frugtplukkere:
L = 100 + 0. 3X1 − 0. 2 X2
kroner/time.
Benyt stikprøven til at finde estimater for timelønnens middelværdi E( L)
og spredning σ( L)
.

Flerdimensional stokastisk variabel
Opgave 11.5 (poolet estimat)
Koncentrationen af et stof A blev målt i 3 partier råvarer:
Råvare 1: 56, 60, 54, 49, 61
Råvare 2: 78, 73, 80
Råvare 3: 66, 62, 70, 72, 60
Det antages, at der er samme spredning i de 3 tilfælde. Find et estimat for spredningen .
Opgave 11.6 (poolet estimat)
Koncentrationen af et stof A blev målt i 2 levnedsmidler:
Levnedsmiddel 1: 87, 89, 94, 86, 89, 95 Levnedsmiddel 2: 93, 99, 94, 91, 98 .
Det antages, at der er samme spredning i de 2 tilfælde. Find et estimat for spredningen .
Opgave 11.7 (poolet estimat)
Koncentrationen af et stof A blev målt i mælken fra 5 køer:
Ko 1: 44, 48, 46, 43, 45 Ko 2: 40, 38, 41
Ko 3: 43, 45, 42, 42
Ko 5: 50
Ko 4: 36, 32
Det antages, at der er samme spredning i de 5 tilfælde. Find et estimat for spredningen .
130
s pool
s pool
s pool
σ
σ
σ

Statistiske beregninger på lommeregner og PC-er
STATISTISKE BEREGNINGER PÅ LOMMEREGNERNE TI89
og TI83 SAMT PÅ PC-PROGRAMMERNE EXCEL, MAPLE OG
MATHCAD
TI 89
1) Generelt:
Metode 1: Vælg HOME\ CATALOG,, F3\ vælg den ønskede fordeling\ENTER
(benyt evt. ALPHA,+ forbogstav for hurtigt at komme til det ønskede navn).
Fordel: Hurtig ved beregning af sandsynligheder, såsom P(X < 0.87) da resultatet straks
indsættes på HOME-linien.
Ulempe: Man skal huske parametrenes rækkefølge (de kan dog ses nederst på skærmen
Metode 2: Vælg APPS\ Stats/List\ indtast eventueller data i eksempelvis “list1" \ vælg en relevant “F- knap”.
Fordel: Der fremkommer nu en menu, som er næsten selvforklarende.
Ulempe: Skal resultatet ned på HOME-linien (man vil regne videre), bliver det lidt besværligt:
HOME, Var-Link\I StatsVar mappen markeres den ønskede størrelse, ENTER
Oprette en “Folder”: VAR-Link\ F1\ 5: Create Folder\ Skriv navn på folder.
Vælg en mappe som den aktuelle mappe: MODE\ Current Folder\navn
Formål: Det kan være praktisk ikke at gemme alle sine resultater i MAIN.
2) Sandsynlighedsfordelinger.
Normalfordeling n( µ , σ )
a) Find p = P( a ≤ X ≤b)
, hvor a ,b, µ , σ er givne konstanter. p = normcdf( ab , , µ , σ )
Eksempel: p = P( X ≤116
. ) , hvor µ = 113 ., σ = 5 p = normcdf( − ∞ ,11.6, 11.3,5) = 0.524
b) Find : ( ≤ ) = , hvor p, µ , σ er givne konstanter. x p =invNorm( p, µ , σ )
x p
P X xp p
Eksempel: P( X ≤ xp) = 07 . ,hvor µ = 11,, 4 σ = 6 x p =invNorm(0.7,11.4,6) =14.55
t - fordeling. Lad T være t - fordelt med frihedsgradstallet f.
a) Find p = P( a ≤T ≤b)
, hvor a og b er givne konstanter. tCdf(a,b,f)
Eksempel: p = P( T ≤ −13
. ) , med f = 14 p = tCdf(- ∞ ,-1.3,14) = 0.1073
b) Find tα ( f ): P( T ≤ tα ( f )) = α ( α given konstant). invt( α ,f )
Eksempel: t0975 . ( 12)
= invt(0.975,12) = 2.179
χ fordeling. Lad Q være fordelt med frihedsgradstallet f.
2 − χ 2 −
a) Find p= P( a ≤Q≤b) , hvor a og b er givne konstanter. p = chi2Cdf(a,b,f)
Eksempel:Find p = P( Q≥27.
3)
, med f = 19 p = chi2Cdf(27.3, ∞ ,19) = 0.0979
2
b) Find fraktilen χα ( f ) : PQ ( ≤ χ ( f))
= α ( given konstant). invChi2( ,f)
α 2 α α
2
Eksempel: χ 0. 025 () 8 = invChi2(0.025,8) = 2.18
Binomialfordeling. Lad X være binomialfordelt b(n,p)
Find Pl ( ≤ X≤m) , hvor 0 ≤ l < m∧m≤n og l og m er hele tal. binomtCdf(n,p,l,m)
Eksempel :p = P( 3≤X ≤ 6)
hvor n = 10 og p = 0.3 p = binomtCdf(10, 0.3, 3, 6) = 0.6066
µ
Poissonfordeling. Lad X være Poissonfordelt p( )
Find Pl ( ≤ X≤m) , hvor 0 ≤ l < m og l og m er hele tal. poissCdf( µ ,l,m)
Eksempel: p = P( X ≤ 94 ) , hvor µ
= 147.6 p = poissCdf(147.6,0,94) = 0.00002
131

Statistiske beregninger på lommeregner og PC-er
3) Gennemsnit, varians og spredning
Find gennemsnit , varians og spredning af tallene 1, 3, 4, 8
Metode 1. HOME\ MATH\6.Statistics\ Anvendes med få tal og kun ønsker beregning af en enkelt størrelse.
Gennemsnit: Mean (liste) Eksempel : Mean({1,3,4,8}) = 4
Varians: Variance(liste) Eksempel : Variance({1,3,4,8}) = 8.667
Spredning: stdDev (liste) Eksempel : stdDev({1,3,4,8}) = 2.944
Metode 2. APPS\ Stats/List\ Data indtastes i “list1"\ F4\ 1: 1-Var Stats
I menu sættes “List” til “List1" (Benyt evt. Var-Link til at finde List1)
Udskriften består af en række statistiske størrelser. Man finder =4, =2.944
x σ x
4) Hypotesetest og konfidensintervaller
APPS\ STAT/LIST hvorefter eventuelle data indtastes i list1
4.1. Normalfordeling. 1 variabel
a1) Hypotesetest; σ kendt: F6\ 1: Z-Test\
Eksempel: Lad data være gemt i list1: {1,3,4,8} , σ = 3 og H: µ < 5
Vælg Data: I menu: µ 0 =5 , σ = 3 , list = list1, Altern. Hyp µ < µ 0 P-værdi = 0.25
x = 4, σ = 3, n = 10 µ < 5
Eksempel: Opgivet , H:
Vælg Stats: I menu: µ 0 =5 , σ = 3 , x = 4, n = 10 , Altern. Hyp µ < µ 0 P-værdi = 0.145
a2) Konfidensinterval σ kendt: F7\ 1: Z-Interval
Eksempel: Lad data være gemt i list1: {1,3,4,8} , σ = 3
Vælg Data: I menu: σ = 3 , list = list1, C Level =.95
Eksempel: Opgivet x = 5, σ = 3, n = 10,
C Int =[1,05; 6.54]
Vælg Stats: I menu: σ = 3 , x = 5, n = 10
C Int =[3.14;6.85]
b1) Hypotesetest; σ ukendt: F6\ 2: T - Test\
Eksempel: Lad data være gemt i list1: {1,3,4,8} H: µ < 5
µ 0 µ µ
Vælg Data: I menu: =5 , list = list1, Altern. Hyp < 0
P-værdi = 0.27
Eksempel: Opgivet x = 4, s= 3, n = 10,
H: µ < 5
Vælg Stats: I menu: µ 0 =5 , x = 4, s= 3, n = 10,
Altern. Hyp µ < µ 0 P-værdi = 0.160
b2) Konfidensinterval σ ukendt: F7\ 1: T-Interval
Eksempel: Lad data være gemt i list1: {1,3,4,8}
Vælg Data: I menu: list = list1, C Level =.95 C Int =[-0.684; 8.684]
Eksempel: Opgivet x = 4, s= 3, n = 10,
Vælg Stats: I menu: x = 4, s= 3, n = 10
C Int =[1.85;6.15]
4.2. Binomialfordeling.
a1) Hypotesetest: F6, 5: 1-Prop-ZTest (Kræver der kan approksimeres til normalfordeling)
Eksempel: X er binomialfordelt b(24, p) , x = 13, H: p > 0.3
Vælg: p0= 0.3, Successes = 13, n= 24, Alternate Hyp : prop > po P -værdi = 0.00489
a2) Konfidensinterval: F7, 5: 1-Prop-ZInt (Kræver der kan approksimeres til normalfordeling)
Eksempel: Af 24 forsøg de 13 en succes:
Vælg: Successes = 13, n= 24, C Int =[0.34; 0.74]
Poissonfordeling: findes ikke, så her må formel for konfidensinterval benytttes
5. Normalfordeling. 2 variable
a1) Hypotesetest; F6\ 4: 2-SampTtest\ udfyld menu (se eksempel 7.1 eller 7.2)
Konfidensinterval: F7\ 4: 2-SampTint\ udfyld menu(se eksempel 7.1)
132

133
Excel
Excel
1) Generelt
Forudsætninger.
Da ikke alle de anvendte statistiske funktioner er indbygget fra starten, skal man først vælge et tilføjelsesprogram:
I Excel 2003: Vælg “Funktioner”, “Tilføjelsesprogrammer”, marker “Problemløser”
I Excel 2007: Vælg “Excel-Office-knappen”, “Excel indstillinger (findes forneden)”, Tilføjelsesprogrammer”,
”Udfør”, ”marker Problemløser”, “Installer”.
Inddata.
Vi vil i det følgende for kortheds skyld antage, at den første stikprøves værdier står i cellerne A1, A2, A3 . . . A10.
Kræves der flere variable vil den næste stå i cellerne B1, B2, B3 . . . B8, osv.
Man angiver “udskriftsområdet” eller “inputområdet” f.eks en søjle placere i cellerne A1:A10 ved
a) at markere området A1 til A10
b) at skrive eksempelvis A1:A10
c) at give det et navn: Vælg “Indsæt” i Excel 2003: Navn i Excel 2007:Formler Definer i menu skriv søjlens
navn og (nederst)A1:A10
Skrive , beregne og kopiere formler.
Vælg den celle hvor resultatet skal stå. Lad det være B1: På værktøjslinien foroven skriv = formel skrives
ENTER Resultatet står nu i celle B1
Hvis selve formlen skal stå i en anden celle. Lad det være A1: Cursor placeres i B1 I formelfelt markeres formlen
uden lighedstegn og man kopierer den (CTRL C)” ENTER (så formlen igen er beregnet i B1 Cursor over i A1
og paste (CTRL V)
Udskrive gitterlinier og række og kolonneoverskrifter
Excel 2003: Vælg Filer Sideopsætning Ark Marker gitterlinier marker række- og kolonneoverskrifter.
Excel 2007: Vælg Sidelayout Under“Gitterlinier” marker “Udskriv” Under “Overskrifter” marker “Udskriv”
2: Indsætte og tegne diagrammer
Lagkage eller søjle: se eksempel 2.1 side 2
Kurve: se eksempel 2.4 side 4
Tegne histogram: se eksempel 2.5 side 6
3: Beregne statistiske størrelser og funktioner
Beregning af “Karakteristiske tal” (se evt. side 11)
Data indtastes i eksempelvis søjle A1 til A10
Excel 2003: Funktioner Dataanalyse Beskrivende statistik udfyld inputområde Resumestatistik
Excel 2007: Data Dataanalyse Beskrivende statistik udfyld inputområde Resumestatistik
Valg af statistiske størrelser (funktioner)
1) Vælg den celle hvor resultatet skal stå (eksempelvis A1).
2) På værktøjslinien foroven:
2a) Tryk på
f x
2b) På den fremkommne menu vælges den ønskede funktion eksempelvis “NORMALFORDELING”
2c) Der fremkommer en menu med anvisning på, hvordan den skal udfyldes.
Gennemsnit, spredning, median, kvartil
Navnene anføres nedenunder, men den fremkomne menu gør det let at indsætte de rette parametre.
Gennemsnit x = MIDDEL(A1:A10)
Spredning s = STDAFV (A1:A10)
Median m = MEDIAN(A1:A10) (= KVARTIL(A1:A10;2) )
1. Kvartil = KVARTIL(A1:A10;1)
Fakultet, kombination, Permutation (se evt. side 80)
Fakultet n! = FAKULTET(n) Eksempel: 5! =FAKULTET(5) = 120

Statistiske beregninger på lommeregner og PC-er
Kombination K(n,p) = KOMBIN(n;p) Eksempel: K(5,3)==KOMBIN(5;3) = 10
Permutation P(n,p = PERMUT(n;p) Eksempel: P(5,3) = PERMUT(5;3) = 60
Normalfordeling.
Lad X være normalfordelt med middelværdi µ og spredning σ
1) P( X ≤ x)
= NORMFORDELING(x ; µ ; σ ;1)
2) P( X ≥ x)
= 1 - NORMFORDELING(x ; µ ; σ ;1)
3) Pa ( ≤ X≤ b) = P( X≤ b) − P( X≤ a)
= NORMFORDELING(b ; µ ; σ ;1) -NORMFORDELING(a ; µ ; σ ;1)
Fraktil x p : P( X ≤ x ) = p⇔
NORMINV(p; µ ; σ )
p
Eksempel: u0975 . = NORMINV(0,975;0;1) = 1,959961
t - fordeling. (se evt. side 44)
Lad T være t - fordelt med f frihedsgrader..
1) PT ( ≥ t)
= TFORDELING(abs(t); f ;1)
(bemærk: TFORDELING(abs(t); f ;1) udregner “øvre hale” af fordelingen)
2) PT ( ≤−t) + PT ( ≥ t)
= TFORDELING(abs(t); f ;2) (udregner “halen” til begge sider)
Fraktil
tα ( f ) = TINV(2(1 - α ) ; f) , α > 0.5
tα ( f ) = - TINV(2 α ; f) , α < 0.5
α
Bemærk: TINV( α ;f) udregner “øvre hale”, svarende til 1 -
2
Bemærk: Man må må udnytte symmetrien i t-fordelingen, for værdier mindre end 0 (svarende til α < 0.5)
Eksempel:
Lad T være t - fordelt med 12 frihedsgrader
1) P( X ≤−1) = P( X ≥ 1)
= TFORDELING(abs(-1);12;1) = 0,168525
2) t0 975 12 = TINV(0,05;12) = 2,178813
. ( )
t0. 025 ( 12)
χ - fordeling. (se evt.side 49)
2
= - TINV(0,05;12) = - 2,178813
Lad X være χ - fordelt med f frihedsgrader
2
P( X ≥ x)
= CHIFORDELING(x;f)
(bemærk: CHIFORDELING(x;f) udregner “øvre hale” af fordelingen)
Fraktil
2
χα ( f ) =CHIINV(1- α ;f)
(bemærk: CHIINV( α ;f) udregner “øvre hale”)
Eksempel:
Lad X være χ - fordelt med 8 frihedsgrader
2
1) P( X ≤ 5)
= 1- CHIFORDELING(5;8) = 0,242424
2)
2
() 8 =CHIINV(0,025;8) = 17,53454
χ 0. 975
2
χ 0. 025
() 8 =CHIINV(0,975;8) = 2,179725
Hypergeometrisk fordeling (se evt. side 88)
Lad X være hypergeometrisk fordelt med parametrene N, M og n
P( X = x)
= HYPGEOFORDELING(x ; n ; M ; N)
Eksempel: Lad N = 600, M = 10 og n = 25
P( X ≤ 1)
= HYPGEOFORDELING(1;25;10;600)+HYPGEOFORDELING(0;25;10;600) = 0,938876
Binomialfordeling ( se evt. side 91)
Lad X være binomialfordelt med parametrene n og p
P( X = x)
= BINOMIALFORDELING(x ; n; p; 0)
P( X ≤
x)
= BINOMIALFORDELING(x ; n; p; 1)
134

Eksempel (jævnfør eksempel 72)
Lad X være binomialfordelt med n = 6 og p = 0.15
P( X = 3)
= BINOMIALFORDELING(3;6;0,15;0) = 0,041453
P( X ≥ 3) = 1- P( X ≤ 2)
=1 - BINOMIALFORDELING(2;6;0,15;1) = 0,047339
Poissonfordeling (se evt. side 97)
Lad X være Poissonfordelt med middelværdien µ
P( X = x)
= POISSON(x; µ ; 0)
P( X ≤ x)
= POISSON(x; µ ; 1)
Eksempel
Lad X være Poissonfordelt med middelværdien 10
P(X = 4) = POISSON(4; 10;0) = 0.018917
P( X ≥ 4)
= 1 - POISSON(4;10;1) = 0,970747
Eksponentialfordeling
Lad T være eksponentialfordelt med middelværdien µ .
PT ( ≤ t)
= EKSPFORDELING(t,1/ µ ,1)
Eksempel:
Lad T være eksponentialfordelt med middelværdi µ =2
PT ( ≤ 3)
=
Konfidensintervaller
EKSPFORDELING(3;1/2;1) = 0,77687
Konfidensinterval middelværdi for 1 normalfordelt variabel. kendt eksakt
σ
Radius r i et 95% konfidensinterval for µ : x ± r = x ± u0975
. (se evt. side 42)
n
r = KONFIDENSINTERVAL(0,05; σ , n).
Eksempel. Lad stikprøven have n =6 værdier, lad spredning σ = 0.25 og gennemsnit x =8
r =KONFIDENSINTERVAL(0,05;0,25;6). Resultat 0,200038
95% konfidensinterval: 8,0 ± 0.200
Konfidensinterval for middelværdi for 1 normalfordelt variabel . σ ikke kendt eksakt
se side 45
Konfidensinterval for sandsynlighed p for 1 binomialfordelt variabel.
se side 93
Hypotesetest
1 normalfordelt variabel
σ kendt eksakt se eksempel 6.1 side 55
σ ikke kendt eksakt se eksempel 6.2 side 56
2 normalfordelte variable
1) Ikke parvise observationer:
data givet: se Excel-program i eksempel 7.1 side 67
data ikke givet: se Excel-program i eksempel 7.2 side 69
2) Parvise observationer:
se Excel-program i eksempel 7.3 side 70
1 binomialfordelt variabel
se eksempel 9.6 side 92
135
σ
Excel

Statistiske beregninger på lommeregner og PC-er
TI 83
1) Sandsynlighedsfordelinger.
Man vælger 2nd DISTR
Normalfordeling n( )
µ , σ
a) Find p = P( a ≤ X ≤b)
, hvor a ,b, µ , σ er givne konstanter. p = normcdf( ab , , µ , σ )
Eksempel: p = P( X ≤116
. ) , hvor µ = 113 ., σ = 5
Bemærk: nedre grænse er sat til -1000
p = normcdf(-1000,11.6, 11.3,5) = 0.524
b) Find x p : P( X ≤ x ) = p,
hvor p, µ , σ er givne konstanter. x p =invNorm( p, µ , σ)
p
Eksempel: P( X ≤ xp) = 07 . ,hvor µ = 11,, 4
t - fordeling.
Lad T være t - fordelt med frihedsgradstallet f.
σ = 6
x p =invNorm(0.7,11.4,6) =14.55
a) Find p = P( a ≤T ≤b)
, hvor a og b er givne konstanter. tCdf(a,b,f)
Eksempel: p = P( T ≤ −13
. ) , med f = 14 p = tCdf(- ∞ ,-1.3,14) = 0.1073
b) Find tα ( f ): P( T ≤ tα ( f )) = α ( α given konstant).
Kan ikke findes dirkte (mærkværdigt) så lettest at slå op i tabel.
Kan dog besværligt findes ved at løse den tilsvarende ligning:
χ 2
Eksempel: Find t0975 . ( 12)
Vi løser ligningen tCdf(-100,x,12)-0.975=0 med hensyn til x, idet vi som startgæt vælger 1
CATALOG, solve(tCdf(-100,x,12)-0.975,x,1) Resultat: 2.179
fordeling.
a) Find p= P( a ≤Q≤b) , hvor a og b er givne konstanter. p = chi2Cdf(a,b,f)
Eksempel:Find p = P( Q≥27.
3)
, med f = 19 p = chi2Cdf(27.3,1000,19) = 0.0979
2
b) Find fraktilen χα ( f ) : PQ ( ≤
som ovenfor.
χ ( f))
= α ( given konstant).Findes ikke, så enten tabelopslag eller løse ligning
α 2 α
Binomialfordeling.
Lad X være binomialfordelt b(n,p)
Find Pl ( ≤ X≤m) , hvor 0 ≤ l < m∧m≤n og l og m er hele tal. binomtCdf(n,p,l,m)
Eksempel :p = P( 3≤X ≤ 6)
hvor n = 10 og p = 0.3
p = binomtCdf(10, 0.3, 6)- binomtCdf(10, 0.3, 2)= 0.6066
Poissonfordeling.
Lad X være Poissonfordelt p( µ )
Find Pl ( ≤ X≤m) , hvor 0 ≤ l < m og l og m er hele tal. poissCdf( µ ,l,m)
Eksempel: p = PX ( ≤ 94 ) , hvor µ = 147.6 p = poissCdf(147.6,94) = 0.00002
Find gennemsnit , varians og spredning af tallene 1, 3, 4, 8
Metode 1. List\ MATH\
Anvendes hvis man har få tal og kun ønsker beregning af en enkelt størrelse.
Gennemsnit: Mean (liste) Eksempel : Mean({1,3,4,8}) = 4
Varians: Variance(liste) Eksempel : Variance({1,3,4,8}) = 8.667
Spredning: stdDev (liste) Eksempel : stdDev({1,3,4,8}) = 2.944
Metode 2. STAT\ Edit
I listen L1 skrives 1 ENTER 3 ENTER 4 ENTER 8 ENTER (slet eventuelle allerede indtastede tal med DEL
STAT hvorved cursor står på CALC. ENTER vælg 1 -Var STATS ENTER
2nd L1 ENTER Resultat blandt meget andet: =4 og = 2.9439
136
x s x
Beregn binomialkoefficient K(8,3) = 8 MATH, PROB, nCr 3. ENTER Resultat 560
2. Hypotesetest og konfidensintervaller
Eventuelle data indtastes i list1. Derefter vælges STAT, TESTS

2.1. Normalfordeling.
a1) Hypotesetest\ σ kendt: 1: Z-Test
Eksempel: Lad data være gemt i list1: {1,3,4,8} , σ = 3 og H: µ < 5
137
TI - 83
Vælg Data: I menu: µ 0 =5 , σ = 3 , List = L1, µ < µ 0 CALCULATE P-værdi = 0.25
x = 4, σ = 3, n = 10 µ < 5
Eksempel: Opgivet , H:
Vælg Stats: I menu: µ 0 =5 , σ = 3 , x = 4, n = 10 , µ < µ 0
P-værdi = 0.145
a2) Konfidensinterval σ kendt: 7: Z-Interval
Eksempel: Lad data være gemt i list1: {1,3,4,8} ,σ = 3
Vælg Data: I menu: σ = 3 , list = L1, C Level =.95
Eksempel: Opgivet x = 5, σ = 3, n = 10,
C Int =[1,05; 6.54]
Vælg Stats: I menu: σ = 3 , x = 5, n = 10
C Int =[3.14;6.86]
b1) Hypotesetest; σ ukendt: 2: T - Test\
Eksempel: Lad data være gemt i list1: {1,3,4,8} H: µ < 5
µ 0 µ µ
Vælg Data: I menu: =5 , list = L1, < 0
P-værdi = 0.27
Eksempel: Opgivet x = 4, s= 3, n = 10,
H: µ < 5
Vælg Stats: I menu: µ 0 =5 , x = 4, s= 3, n = 10,
µ < µ 0
P-værdi = 0.160
b2) Konfidensinterval σ ukendt: 8: T-Interval
Eksempel: Lad data være gemt i list1: {1,3,4,8}
Vælg Data: I menu: list = list1, C Level =.95 C Int =[-0.684; 8.684]
Eksempel: Opgivet x = 4, s= 3, n = 10,
Vælg Stats: I menu: x = 4, s= 3, n = 10
C Int =[1.85;6.15]
2.2. Binomialfordeling.
a1) Hypotesetest: 5: 1-Prop-ZTest (Kræver der kan approksimeres til normalfordeling)
Eksempel: X er binomialfordelt b(24, p) , x = 13, H: p > 0.3
Vælg: p0= 0.3, x = 13, n= 24, prop > po P -værdi = 0.00489
a2) Konfidensinterval: A: 1-Prop-ZInt (Kræver der kan approksimeres til normalfordeling)
Eksempel: Af 24 forsøg er de 13 en succes:
Vælg: x = 13, n= 24, C Int =[0.34; 0.74]
Poissonfordeling: findes ikke, så her må formel for konfidensinterval benyttes

Statistiske beregninger på lommeregner og PC-er
MAPLE
Beregn gennemsnit og spredning af tallene 1 3 4 8
> with(stats):
data:=[1,3,4,8];
data := [1, 3, 4, 8]
> describe[mean](data);
4
> describe[standarddeviation[1]](data);
Beregne korrelationskoefficient for den i eksempel 9.2 nævnte stikprøve
(1,2), (0,0), (2,2), (2,2), (1,0), (2,2), (0,2), (2,2), (0,2), (2,2) .
Programudførelse:
> data1:=[1,0,2,2,1,2,0,2,0,2]; x- værdier
data1 := [1, 0, 2, 2, 1, 2, 0, 2, 0, 2] udskrift
> data2:=[2,0,2,2,0,2,2,2,2,2]; y-værdier
data2 := [2, 0, 2, 2, 0, 2, 2, 2, 2, 2] udskrift
> describe[linearcorrelation](data1,data2): evalf(");
.4014775343 resultat
Normalfordeling.
Find for n(113.3,5.6) P( X ≤ 116.1) .
Programudførelse:
> with(stats):
> with(statevalf):
> cdf[normald[113.3,5.6]](116.1);
Facit .6914624613
χ 2
fordeling.
Find en tests P-værdi: P( Q ≥ 27.26) idet frihedsgradstallet er 19 (jævnfør eksempel 5.6)
Programudførelse:
> with(stats):
> with(statevalf):
> 1-cdf[chisquare[19]](27.36);
Facit: .0965431211
t - fordeling.
Find en tests P-værdi: PT ( ≤ -1.31) idet frihedsgradstallet er 14 (jævnfør eksempel 5.5)
Programudførelse:
> with(stats):
> with(statevalf):
> cdf[studentst[14]](-1.31);
Facit: .1056420798
Find for binomialfordelingen b(100,0.3) P( X ≤ 35)
Programudførelse:
> with(stats):
> with(statevalf):
> dcdf[binomiald[100,0.3]](35);
Facit: .8839213940
138

MATHCAD
1) Generelt:
Sandsynlighedsfunktioner :
Skriv funktionens navn eller vælg fra (øverste) værktøjslinie
f ( x)
\Probability Density (dfunktionsnavn). Tæthedsfunktion PX ( = a)
,
f ( x)
\Probability Distribution (pfunktionsnavn). Fordelingsfunktion PX ( ≤ a)
eller
f ( x)
\Probability Distribution (qfunktionsnavn) Invers tæthedsfunktion: P( X ≤ xp) = pFind
x p .
Rækkefølgen af parametrene kan findes ved at placere cursor på navnet og trykke på tasten F1.
2) Sandsynlighedsfordelinger.
Normalfordeling n( µ , σ )
p = P( a ≤ X ≤b)
µ , σ
139
MATHCAD
a) Find , hvor a ,b, er givne konstanter.
p= P( a≤ X ≤ b) = P( X ≤b) − P( X ≤ a)
= pnorm(b, µ , σ ) - pnorm(a, µ , σ )
Eksempel: p = P( X ≤116
. ) , hvor µ = 113 ., σ = 5
p = pnorm(11.6, 11.3,5) = 0.524
b) Find x p : P( X ≤ x ) = p,
hvor p, µ , σ er givne konstanter. x p =qnorm( p, µ , σ )
p
Eksempel: P( X ≤ xp) = 07 . ,hvor µ = 11,, 4 σ = 6
x p =qnorm(0.7,11.4,6) =14.55
t - fordeling.
Lad T være t - fordelt med frihedsgradstallet f.
a) Find p = P( a ≤T ≤b)
, hvor a og b er givne konstanter.
p= P( a≤ X ≤ b) = P( X ≤b) − P( X ≤ a)
= pt(b,f) -pt(a,f)
Eksempel: p = P( T ≤ −13
. ) , med f = 14 p = pt(-1.3,14) = 0.1073
b) Find tα ( f ): P( T ≤ tα ( f )) = α ( α given konstant). tα ( f ) = qt( α ,f )
Eksempel: t0975 . ( 12)
= qt (0.975,12) = 2.179
χ 2 −
fordeling.
Lad Q være χ fordelt med frihedsgradstallet f.
2 −
a) Find p= P( a ≤Q≤b) , hvor a og b er givne konstanter. p = pchisq(b,f) - pshisq(a,f)
Eksempel:Find p = P( Q≥27.
3) , med f = 19 p= 1− P( Q≤273
. ) =1- pchisq(27.3,19) = 0.0979
2
b) Find fraktilen χα ( f ) : PQ ( ≤ χ ( f))
= α ( given konstant). f = qchisq( α ,f )
α 2 α χ α 2 ( )
2
Eksempel: χ 0. 025 () 8 = qchisq(0.025,8) = 2.18
Binomialfordeling.
Lad X være binomialfordelt b(n,p)
a) P(X=x) =dbinom(x,n,p)
P( X ≤ x)
= pbinom(x,n,p)
Eksempel :q = P( 3≤ X ≤6)
, hvor n = 10 og p = 0.3
q = P( X≤6) − P( X≤2)
= pbinom(6,10, 0.3)-pbinom(2,10,0.3) = 0.6066
b) Find det hele tal m for hvilket P( X≤ m)
=α m = qbinom(p, n, α )
Eksempel: Lad X være binomialfordelt med p = 0.3 og n = 10.
Find det hele tal m for hvilket PX ( ≤ m)
=095
.
m = qbinom(0.3, 10,0.95 ) = 9

Statistiske beregninger på lommeregner og PC-er
Poissonfordeling.
Lad X være Poissonfordelt p( )
µ
a) P(X=x) =dpois(x, µ )
P( X ≤ x)
= ppois(x, µ )
Eksempel: p = , hvor = 147.6 p = ppois(94,147.6) = 1.54 10-6 P( X≤
94 ) µ ⋅
b) Find det hele tal m for hvilket P( X≤ m)
=α m = qpois( α , µ )
Eksempel: Lad X være Poissonfordelt med = 147.6.
µ
Find det hele tal m for hvilket PX ( ≤ m)
=095 .
m = qpois(0.95, 147.6 ) =168
Hypergeometrisk fordeling:
Lad X være hyprgeometrisk fordelt h(N,M,n)
a) P(X=x) =dhypgeo(x,M, N-M,n)
P( X ≤ x)
= phypgeo(x,M,N-M,n)
3) Gennemsnit, varians og spredning
Find gennemsnit , varians og spredning af tallene 1, 3, 4, 8
⎛1⎞
⎜ ⎟
⎜ 3⎟
Opret en søjlematrix v:=
⎜4⎟
⎜ ⎟
⎝8⎠
Vælg fra værktøjslinie f ( x)
\ Category: Statistics \ Function Name: eksempelvis mean
Eksempel : Gennemsnit: mean (v) =4 Mean({1,3,4,8}) = 4
Varians: Var(v) = 8.667
Spredning: Stdev (v) = 2.944
140

APPENDIX . Oversigt over approksimationer.
1
10
n
N
p ≤ 1
10
≤ 1
10
9
< p< ∧5≤n⋅p≤n−5 10
n 1 M 1
1) Når > og ≤ benyttes, at hNMn ( , , ) = hNnM ( , , ) .
N 10 N 10
141
M
N
APPENDIX
2) For p ≥ benyttes, i stedet for at tælle Xgammel = “antal af successer”, så at tælle X = antal fiaskoer dvs.
9
10
p = 1 − pgammel
og X = n − Xgammel
.
3) Husk heltalskorrektion ved approksimation med normalfordeling. (se næste side)

APPENDIX
Approksimation af binomialfordeling til normalfordeling.
Det kan vises, at tæthedsfunktionen for binomialfordelingen b (n, p) nærmer sig ubegrænset til normalfordelingen
, hvor og , når n vokser ubegrænset1) n( µ , σ ) µ = n ⋅ p σ = n⋅ p⋅( 1−
p)
.
Approksimation af en binomialfordeling med en normalfor-
1 9
deling anses, når < p < i praksis for at være tilfreds-
10 10
stillende, såfremt n⋅ p≥5(og
n⋅( 1− p)
≥5).
Da binomialfordelingen kun antager heltalsværdier,
medens en normalfordeling kan antage alle værdier på
talaksen, svarer hvert helt tal ved binomialfordelingen til et
interval af længden 1 ved normalfordelingen. På figur 1 er
derfor tegnet en firkant, der har bredden 1, og hvis højde er
P( X = 4)
udregnet ved binomialfordelingen. Arealet
under normalfordelingskurven fra x = 3.5 til x = 4,5 er med
tilnærmelse lig firkantens areal. Man siger, at man ved
approksimationen må heltalskorrigere (korrigeres for
Fig. 1. Heltalskorrektion
kontinuitet).
Ved approksimationen benyttes derfor følgende anførte formler, gældende for en binomialfordelt variabel X fordelt
1 9
b (n, p), hvor ≤ p ≤ og 5≤n⋅ p≤n−5. 10 10
Eksempel 7.13: Approksimation af binomialfordeling med normalfordeling.
En kunde til de i eksempel 2.3 producerede plastikkasser køber kasserne i partier på 2000. Kunden godkender
et parti efter en stikprøvekontrol, hvor der udtages 100 kasser. Hvis antallet af defekte kasser i stikprøven højst
er 14 godkendes hele partiet. I modsat fald kasseres partiet.
Hvor stor er sandsynligheden for at et parti bliver godkendt, hvis der er 300 defekte kasser i hele partiet på de
2000.
Løsning:
Lad X være antallet af defekte kasser i stikprøven. Vi ønsker at udregne P( X ≤ 14)
.
Umiddelbart er X hypergeometrisk fordelt med N = 2000, M = 300, og n = 100.
⎛ n 100 1 ⎞
Da stikprøvestørrelsen er lille ⎜ = < ⎟ kan fordelingen af X umiddelbart approksimeres med
⎝ N 2000 10⎠
binomialfordelingen b (100, p), hvor p . Dette giver ved benyttelse af en lommeregner som
M 300
= = = 015 .
N 2000
TI-89 at P( X ≤ 14)
= 45.72%.
Idet n⋅ p=
15 > 5 , kan i stedet for approksimeres med normalfordelingen med µ = 15 og σ = 15⋅ 085 . = 357 . .
Ved hjælp af denne approksimation kan vi beregne:
P( X ≤ 14)
= normCdf( −∞,
14.5, 15, 3.57) = 44.43%
Det ses, at der er ca. 1.5 % afvigelse, hvilket normalt ingen betydning har.
1) Matematisk formulering: Når X er fordelt b(n, p), vil for den tilsvarende normerede variabel
Y =
X −n⋅ p
n⋅ p⋅( 1 − p)
gælde, at PY ( ≤ y) ⎯ ⎯→∞→ ( y)
for ethvert tal y.
Φ
n
142

u p
Tabel over fraktiler i normeret normalfordeling
Tabel over fraktiler i normeret normalfordeling n( 01 , ) . PU ( ≤ u ) = p.
Bemærk: u p = - u 1 - p
p 0.0005 0.001 0.005 0.01 0.025 0.05 0.10
u p
-3.291 -3.090 -2.576 -2.326 -1.960 -1.645 -1.282
p 0.90 0.95 0.975 0.99 0.995 0.999 0.9995
u p
Eksempel: u 0.975 = 1.960
1.282 1.645 1.960 2.326 2.576 3.090 3.291
143
p

Facitliste
FACITLISTE
KAPITEL 2
2.1 -
2.2 -
2.3
2.4 (1) - (2) ca 24%
2.5 (1) - (2) ca 0.052
2.6 (1) - (2) ca 13%
2.7 (1) - (2) 24.8 24.5
2.8 (1) - (2) - (3) -
KAPITEL 3
3.1 (1) - (2) - (3) 0.833 0.3056 0.5528 (4) 0.1641
3.2 (1) - (2) - (3) 1.5 0.75 0.866 (4) 0.088
3.3 65 0.4
3.4 1658.76 57.31 3.46%
3.5 103.32 2.6 2.52%
3.6 996.3 46.36 4.65%
3.7 (a) 515 10 (b) 41.8% (c ) (d) 20.9%
6 −
. ⋅
258 10 4 −
. ⋅
KAPITEL 4
4.1 (1) 0.7734 0.0548 0.1718 (2) 0.7480
4.2 (1) 69.15% (2) 10.88% (3) 112.2 (4) 117.3 6.535
4.3 (1) 86.64% (2) 0.008 (3) 0.020
4.4 (1) 5.94% (2) 27.71% (3) [783.51; 816.49]
4.5 (1) 9.5 1.265 (2) 12.45 (3) 2.41%
4.6 (1) 92.8%
4.7 (1) 97.71% (2) 25.45
4.8 (1) 65 0.4 (2) 77.34%
KAPITEL 5
5.1 (1) 12.13 0.6783 (2) [11.65 ; 12.61] (3) [10.52 ; 13.74] (4) [11.73 ; 12.53]
5.2 (1) 2259.92 35.569 (2) [2237 ; 2283] (3) [2178 ; 2341]
5.3 (1) 74.0362 0.00124 (2) [74.035; 74.037] (3) [74.036 ; 74.037]
5.4 (1) 750.2 (2) [740.1 ; 760.3] (3) 19.13 (4) [14.0 ; 30.2]
5.5 (1) 7.83 0.363 (2) [7.45 ; 8.22] (3) 53
5.6 [25.21 ; 60.36]
5.7 [0.00083 ; 0.00231]
5.8 (a) [4.23 ; 4.29] (b) 22 (c ) [4.16 ; 4.36] (d) [0.028 ; 0.076]
5.9 (1) [0.965 ; 1.111] (2) [0.0263; 0.1714]
144

145
Facitliste
KAPITEL 6
6.1 (1) nej P-værdi = 2.28% (2.67%)
6.2 ja 3.45% (2) 58.0 (3) [55.84; 60.16]
6.3 (1) 84.47 6.85 (2) ja P-værdi = 0.44% (3) [81.27 ; 87.67] (4) 25.7%
6.4 (a)nej P-værdi = 12.1% (b) [7.93 ; 8.49 ]
6.5 (a) ja P-værdi = 0.157% (b) [24.07 ; 35.56]
6.6 nej P-værdi = 6.45%
6.7 (1) ja, P-værdi = 0.012 (2) 0.987 (3) [0.68 ; 1.80 ]
. ⋅
6.8 ja, P-værdi =18 10 9 −
6.9 (1) 19.5 (2) nej, P-værdi =0.1% , (eller P-værdi =0.135%)
6.10 (1) 12 (2) ja P-værdi = 0.48 (3) nej
6.11 (1) 24 (2) ja P-værdi = 0.16% (3) nej [2.59 ; 2.67]
6.12 (1) 26 (2) ja P-værdi = 25 10 (3) ja
13 −
. ⋅
KAPITEL 7
7.1 P - værdi = 0.1044
7.2 (1) P - værdi = 0.001 (2) [0.70 ; 3.12]
7.3 P - værdi = 0.0204
7.4 (1) P - værdi = 0.0714 (2) P - værdi = 0.401
7.5 (1) 18 (2) P - værdi = 0.00017 , [11.9 ; 15.0]
7.6 P - værdi = 0.589
7.7 P - værdi = 0.1398
7.8 (1) nej P-værdi =14.95%
7.9 (1) nej, P-værdi =9.85% (2) [0.22 ;7.28 ]
7.10 (1) - (2) Ja, P-værdi =3.63%
KAPITEL 8
8.1 0.1 0.8 0.2 0.7
8.2 (1) 0.9134 (2) 0.9678
8.3 (1) 8.75% (2) 38.75% (3) 41.25% (4)11.25%
8.4 (1) 6.4% (2) 78.4% (3) 7.2%
8.5 (a) 30.24% (b) 0.24% (c ) 99.76% (d) 4.04% (e) 44.04% (f) 21.44%
8.6 1.283 ⋅ 10 12
8.7 (a) - (b) 736
8.8 (a) 6 (b) 24
8.9 (a) 100 /b) 2400
8.10 60
8.11 (1) 27.1% 36.0% 9.756% (2) 53.34% (3) 49.20%
8.12 3 40
8.13 (1) 5 (2) 9
8.14 30.24%
8.15 910 7
⋅

Facitliste
KAPITEL 9
9.1 (1) - )2) 0.6
9.2 (1) 91.67% (2) 9.167%
9.3 (1) 17.68% (2) 59.28%
9.4 2.58%
9.5 5.83%
9.4 (1) 0.988%
9.5 (1) - 73.75 30.08 (2) 221.25 kr 57.48%
9.6 5.6%
9.7 94.9%
9.8 40.87%
9.9 13%
9.10 nej, P-værdi =0.08%
9.11 (1) 0.9% (2) nej
9.12 (1) ja, P-værdi = 2.53% (2) 0.12 (3) [0.056 ; 0.184]
9.13 ja p = 0.43%
9.14 (1) 0.108 (2) [0.089 ; 0.127]
9.15 [0.799 ; 0.847]
9.16 1522
9.17 77.86%
9.18 (1) 7.94% (2) 11.8%
9.19 (1) (a) 60.6% (b) 91.6% (c) 6.2% (2) 4.4%
9.20 (1) 30.1% (2) 87.9% (3) 4
9.21 50.37%
9.22 (1) 15 (2) 81.9%
9.23 75.3%
9.24 6.56%
9.25 92.2%
9.26 44.6%
9.27 (1) nej P-værdi = 7.84% (2) 100.8 (4) [85.56 ; 116.04]
9.28 (1) 4.68 (2) [4.47 ; 4.89] (3) 69.44
9.29 (1a) 11 (1b) [4.5 ; 17.5] (2a) 1.1 (2b) [0.45 ; 1.75]
9.30 (1) 0.539% (2) 0.119%
9.31 7.31%
9.32 0.188%
KAPITEL 10
10.1 (1) 2.90 (2) 14.6% (3) 16.98
10.2 (1) 77.88% (2) 10.45% (3) 77.88% (4) 9.48%
10.3 1
10.4 (1) 79.8% (2) 99.33% (3) 22.8 (4) 14
146

147
Facitliste
KAPITEL 11
11.1.1 (a1) - (a2) - (a3) nej (a4) 2.3 1.8 1.345 1.470 (a5) 12.6 (b1) 2.2 1.5 1.316
1.5811
11.1.2 (a6) 0.06 0.0304 (b2) 0.6667 0.3203
11.1.3 (a7) 52 15.52 (b3) 53.33 17.51
11.2.1 (a1) - (a2) nej (a3) 0.9 0.5 0.830 0.5 (a4) 0.9707 (b1) 0.6 0.6 0.843
0.516
11.2.2 (a5) 0.15 0.36 (b2) 0.2667 0.6124
11.2.3 (a6) 15300 3716.18 (b3) 15800 4131.18
11.3.1 (a1) - (a2) nej a3) 4.2 3.2 1.4 0.9798 (a4) 0.625 (b1) 4 3.2 1.633 1.033
11.3.2 (a5) 0.16 0.0342 (b2) 0.4444 0.2635
11.3.3 (a6) 316 44.36 (b3) 300 28.28
11.4.1 178.33 71.833 11.428 10,870
11.4.2 100.97 0.8128
11.4.3 139.13 2.089
11.5 4.6344
11.6 3.559
11.7 3.3466

Stikord
STIKORDSREGISTER
A
acceptområde 54
additionssætning
for sandsynligheder 81
for linearkomb. af normalf. variable 30, 35
alternativ hypotese 58
approksimation 104
binomial til normalfordeling 141
binomial til Poissonfordeling 141
hypergeometrisk til binomialford. 100, 141
Poisson til normalfordeling 141
B
bagatelgrænse 60
Bayes sætning 83
betinget sandsynlighed 82
binomialfordeling
binomialfordelingstest 97, 105
både A og B 80
C
centrale grænseværdisætning 39
chi i anden fordeling 49
D
deskriptiv statistik 2
dimensionering 60, 64
diskret variabel 16, 91
E
eksperiment, tilfældigt 15
eksponentialfordeling 115
ensfordelte variable 21
ensidet
binomialtest 97, 105
chi-i-anden test 59
Poissontest 102, 106
t -test 57, 63
test 53
enten A eller B 80
estimat 7
Excel, oversigt 133
148
F
fakultet 85
fejl af type I 59
fejl af type II 59
flerdimensional variabel 120
fordeling
binomial- 94
chi i anden- 49
eksponential- 115
hypergeometrisk- 91
kontinuert 17
logaritmisk normal- 119
normal- 28
rektangulær 113
t- 43
To-dimensional normal- 118
Weibull- 117
fordelingsfunktion
kontinuert variabel 20
foreningsmængde 80
forkastelsesområde 54
fraktil 9, 20
fraktiltabel for normalfordeling 144
frihedsgrad 10
fællesmængde 80
G
Galton apparat 29
Gauss fordeling 29
generaliseret hypergeometrisk ford. 103
gennemsnit 7, 32, 39
H
heltalskorrektion 142
histogram 5, 17
hypergeometrisk fordeling 91
hypotesetest
1 normalfordelt variabel 53
2 normalfordelte variable 70
binomialfordeling 97
Poissonfordeling 102
hyppighed, relativ 7, 15
hændelse 15
additionssætning 81
både A og B 80
enten A eller B 80

Stikord
foreningsmængde 80
fællesmængde 80
ikke A 80
uafhængige 81
I,J
ikke A 80
inferentiel statistik 1
K
karakteristiske tal 7
kombination 86
kombinatorik 84
konfidensinterval 40, 42 , 44, 48, 49
konfidensinterval
1 normalfordelt variabel 40, 42, 44, 48, 49
2 normalfordelte variable , differens 72, 76
binomialfordeling 98, 105
Poissonfordeling 103, 106
kontinuert stokastisk variabel 17
korrelationskoefficient 120, 123
kovarians 120, 23
kvadratregel 21
kvalitative data 2
kvalitetskontrol 34
kvantitative data 4
kvartil 8
kvartilafstand 11
kvartilafstand, relativ 11
L
lagkagediagram 2
levetid 116
linearitetsregel 21
linearkombination 21
logaritmisk normalfordeling 118
lommeregner
TI - 83 137
TI - 89 132
M
Maple 138
Mathcad 139
median 8
middelværdi 7
diskret variabel 91, 95, 191
kontinuert variabel 19
multiplikationsprincip 84
149
N
nedre kvartil 9
n fakultet 85
normalfordeling 28
logaritmisk 118
normeret 31
todimensional 118
nulhypotese 54
O
observationer, parvise 74
opgaver kapitel
2 12
3 26
4 36
5 51
6 66
7 77
8 88
9 107
10 119
11 128
ophobningslov 24
oversigt
kap 5 50
kap6 63
kap 7 76
kap 9 105
P
parvise observationer 74
Poissonfordeling 100
Poissonfordelingstest 102
polynomialfordeling 104
population 1, 17
produktsætning 81, 82
prædistinationsinterval 46
P-værdi 55
R
randomisering 38
rektangulær fordeling 113
relativ hyppighed 7
relativ usikkerhed 23
repræsentativ stikprøve 38
Facitliste

Stikord
S
SAK 10
sandsynlighed 16, 80
additionssætning 81
betinget 82
produktsætning 81
Satterwaithes metode 71
signifikansniveau 54
simpel udvælgelse 38
spredning 9, 32
på gennemsnit 28
SS 10
standard deviation 9
statistisk uafhængige 81
stikprøve 17 , 38
gennemsnit 7, 32
ordnet 85
spredning 9, 32
udvælgelse 38
uordnet 86
varians 9
stikprøvestørrelse 46, 99
stokastisk variabel 16
stratificeret udvælgelse 38
systematisk udvælgelse 38
søjlediagram 3
T
tabel over fraktiler i normalfordeling 143
test
af middelværdi 53, 63
af spredning 59, 65
fejl af type I 59
fejl af type II 59
P-værdi 53
testfunktioner
χ 2
- fordeling 49
t - fordelingen 43
t-fordeling 43
to-dimensional normalfordeling 118
tosidet test 58
Ti-83 136
TI - 89 131
t-test, ensidet 57
tæthedsfunktion
diskret variabel 92, 96
kontinuert variabel 17
150
U
uafhængige hændelser 15
uafhængige stokastiske variable 15
udfald 15
udfaldsrum 15
usikkerhed
maksimal 23
relativ 23
statistisk 23
usikkerhedsberegning 23
U-fordeling 31
V
variabel
binomialfordelt 94
diskret 1
kontinuert 17
stokastisk 16
varians 9
diskret variabel 16, 91
kontinuert variabel 19
variationsbredde 5
W
Weibullfordeling 117
Z
Z - fordeling 31
Ø
øvre kvartil 9