Lineær programmering - Matematik og naturfag i verdensklasse
Lineær programmering - Matematik og naturfag i verdensklasse Lineær programmering - Matematik og naturfag i verdensklasse
Retningsvektoren for linien #12: nf := [80, 65] angiver den retning, hvori funktionen vokser 2 . Kriteriefunktionens værdi vil altså vokse, når linien bevæger sig op til højre. Maximalværdien i mulighedsområdet fås derfor lige før linien slipper, hvilket må ske i et hjørnepunkt (eller liniestykket, der forbinder to hjørnepunkter). På figuren har linien passeret to punkter (A og B), medens der er tre tilbage (C, D og E). Ved at bevæge linien yderligere ses, at det er punktet D, der passeres sidst, hvilket betyder, at kriteriefunktionen opnår sin maximale værdi i mulighedsområdet i dette punkt. Ulighederne i bibetingelserne og positivitetsbetingelserne giver i dette tilfælde anledning til 5 linier, der har 10 skæringspunkter, hvoraf de 5 er hjørner i mulighedsområdet. Da kriteriefunktionens maximalværdi antages i et hjørnepunkt, kunne vi have løst det oprindelige problem ved at finde de 10 skæringspunkter, bestemme hvilke, der ligger i mulighedsområdet, indsætte disse i kriteriefunktionen og vælge den største. Den grafiske (geometriske) metode gør, at vi kun skal finde punktet D, der her er bestemt af den første og sidste ulighed i bibetingelserne: #13: 0.15·x + 0.1·y = 110 0.05·x + 0.05·y = 40 #14: x = 600 y = 200 Disse værdier indsættes i kriteriefunktionen #15: f(600, 200) = 61000 2 Vektorpile kan i Derive tegnes v.h.a. Arrows.mth 5
Hermed bliver svaret på problemet: Der skal produceres 600 skjorter og 200 par bukser (pr. uge) Herved bliver fortjenesten 61000 kr. Hvis vi i ovenstående eksempel forestiller os at fabrikken også fremstillede f.eks. kjoler, ville der i ulighederne indgå tre variable x (skjorter), y (bukser) og z (kjoler). Herudover ville kriteriefunktionen blive en lineær funktion i tre variable f(x,y,z) = ax+by+cz. Det betyder, at en geometrisk fremstilling skulle foretages i et 3-dimensionalt koordinatsystem. Vi illustrerer det 3-dimensionale tilfælde med et lille simpelt eksempel. Eksempel 1.1. Lad bibetingelserne være #16: x + y + z “ 4 #17: 2·y + z “ 4 #18: z “ 3 #19: x “ 2 og positivitetsbetingelserne #20: x ’ 0 y ’ 0 z ’ 0 Vi ønsker at maksimere kriteriefunktionen #21: f(x, y, z) := 2·x + 3·y + 4·z Mulighedsområdet - som bliver et konvekst polyeder - får følgende udseende, set fra forskellige vinkler 3 : For en given funktionsværdi for kriteriefunktionen (f.eks. 10) får vi ligningen for en plan: #22: 2·x + 3·y + 4·z = 10 3 Derive kan ikke i 3 dimensioner grafisk løse ulighedssystemer, så mulighedsområdet er her optegnet ved at finde de relevante hjørnepunkter og forbinde disse på passende vis (se appendiks). 6
- Page 1 and 2: Lineær programmering med Derive B
- Page 3 and 4: Forord. Dette undervisningsmaterial
- Page 5: Uligheden er lineær, hvilket betyd
- Page 9 and 10: Opgave 1.2 Ulighederne i bibetingel
- Page 11 and 12: 2. Simplexmetoden Vi har i de tidli
- Page 13 and 14: Herefter får tabellen følgende ud
- Page 15 and 16: „ x y z s t u v b † ¦ ¦ ¦ 1
- Page 17 and 18: Pivotsøjlen bliver nu x-søjlen, o
- Page 19 and 20: 3. Simplexmetoden med Derive Simple
- Page 21 and 22: Simplex-programmet kan udskrive all
- Page 23 and 24: 4. Skyggepriser og følsomhedsanaly
- Page 25 and 26: #133: sluttabel_max „ 1 † ¦ 0
- Page 27 and 28: #144: D := FORCE0(FORCE0(FORCE0(SCA
- Page 29 and 30: #162: x ’ 0 y ’ 0 Dette LP-pro
Retningsvektoren for linien<br />
#12: nf := [80, 65]<br />
angiver den retning, hvori funktionen vokser 2 .<br />
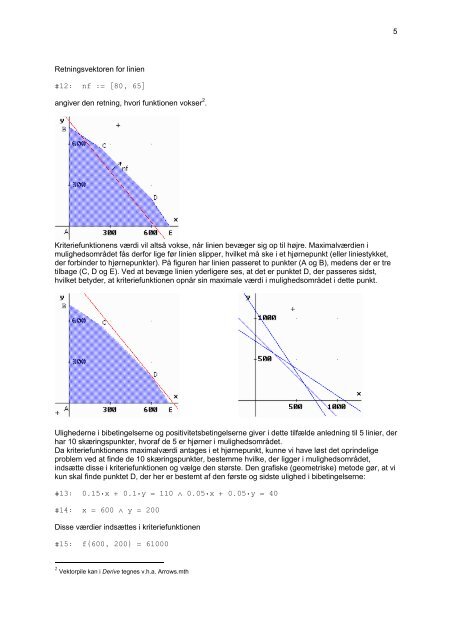
Kriteriefunktionens værdi vil altså vokse, når linien bevæger sig op til højre. Maximalværdien i<br />
mulighedsområdet fås derfor lige før linien slipper, hvilket må ske i et hjørnepunkt (eller liniestykket,<br />
der forbinder to hjørnepunkter). På figuren har linien passeret to punkter (A <strong>og</strong> B), medens der er tre<br />
tilbage (C, D <strong>og</strong> E). Ved at bevæge linien yderligere ses, at det er punktet D, der passeres sidst,<br />
hvilket betyder, at kriteriefunktionen opnår sin maximale værdi i mulighedsområdet i dette punkt.<br />
Ulighederne i bibetingelserne <strong>og</strong> positivitetsbetingelserne giver i dette tilfælde anledning til 5 linier, der<br />
har 10 skæringspunkter, hvoraf de 5 er hjørner i mulighedsområdet.<br />
Da kriteriefunktionens maximalværdi antages i et hjørnepunkt, kunne vi have løst det oprindelige<br />
problem ved at finde de 10 skæringspunkter, bestemme hvilke, der ligger i mulighedsområdet,<br />
indsætte disse i kriteriefunktionen <strong>og</strong> vælge den største. Den grafiske (geometriske) metode gør, at vi<br />
kun skal finde punktet D, der her er bestemt af den første <strong>og</strong> sidste ulighed i bibetingelserne:<br />
#13: 0.15·x + 0.1·y = 110 0.05·x + 0.05·y = 40<br />
#14: x = 600 y = 200<br />
Disse værdier indsættes i kriteriefunktionen<br />
#15: f(600, 200) = 61000<br />
2 Vektorpile kan i Derive tegnes v.h.a. Arrows.mth<br />
5