PDF: Galaxen Nr. 17 - Marts 1998 - SmartData
PDF: Galaxen Nr. 17 - Marts 1998 - SmartData
PDF: Galaxen Nr. 17 - Marts 1998 - SmartData
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
12<br />
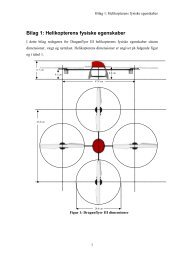
<strong>Nr</strong>. <strong>17</strong> – <strong>Marts</strong> <strong>1998</strong> GALAXEN<br />
selvfølgelig mere speget, fordi den<br />
grafiske lommeregner kun arbejder<br />
med en endelig præcision!<br />
For at afgøre om et lommeregnertal<br />
opfører sig rationalt, skal vi altså<br />
udvikle det i en kædebrøk. Hvis der<br />
fremkommer en endelig kædebrøk er<br />
sagen selvfølgelig i orden. Men på<br />
grund af afrundingsfejl, behøver<br />
resten ikke blive eksakt nul:<br />
Fig. 7<br />
Da 22/7 = 3 + 1/7 består spektret<br />
netop af tallene 3 og 7.<br />
Den tredje heltalsdel 4.76·10 11 skyldes<br />
afrundingsfejl i lommeregneren.<br />
Spørgsmålet er så hvor lille en rest, vi<br />
vil acceptere som værende tæt nok<br />
på nul: Valget af denne grænse giver<br />
et ’filter’, som accepterer nogle<br />
lommeregnertal som opførende sig<br />
rationalt, mens andre forkastes, fordi<br />
de ikke udviser den rette rationale<br />
opførsel.<br />
I praksis ønsker vi selvfølgelig at<br />
genkende så mange rationale tal som<br />
muligt. På den anden side ønsker vi<br />
ikke at genkende et tal som rationalt,<br />
hvis det klart er fremkommet ved en<br />
irrational udregning. Vi skulle helst<br />
holde fingrene fra 100 2 og 1000π.<br />
Nu er de kvadratiske irrationaliteter<br />
ikke noget større problem, fordi de<br />
netop udgør den type tal, som adskiller<br />
sig mest fra de rationale tal. Det<br />
er langt mere problematisk med<br />
transcendente tal som 1000π. For at<br />
få en fornemmelse for problemet,<br />
kan vi starte med at prøve at udregne<br />
spektret for π:<br />
3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 21, 3,<br />
1, 1, 2, 64, 4, 1, 48<br />
(NB! Det er de første tyve tal i lommeregnerens<br />
spektrum – og de stemmer<br />
jo ikke nødvendigvis overens med<br />
tallene i det eksakte spektrum! Faktisk<br />
er det kun de første 12 tal i det<br />
ovenfor anførte spektrum, der er<br />
korrekte). Læg mærke til tallet 292 i<br />
starten, som er overraskende højt!<br />
Det viser, at et filter under fx 1/250<br />
ville lade slippe π igennem som et<br />
rationalt tal!<br />
Prøver vi i stedet med 1000π fås<br />
spektret<br />
3141; 1, 1, 2, 5, 22, 3, 3, 2, 1, 1, 1, 1,<br />
1, 15, 6, 2, 1, 1, 3, 2<br />
Her er det største tal i brøkdelsspektret<br />
givet ved 22, så der er faktisk<br />
ingen fare for at genkende det som<br />
rationalt. (Og derved har vi fundet<br />
endnu en måde at undgå Fracrutinens<br />
fejlagtige genkendelse af<br />
1000π som værende et rationalt tal!)<br />
Et af de virkeligt grimme tal, som<br />
man skal gardere sig mod er π 4 , som<br />
har en usædvanlig lille rest i starten<br />
af kædebrøksudviklingen, idet spektret<br />
indeholder det usædvanligt høje<br />
tal 16539:<br />
Fig. 8<br />
I praksis benytter man derfor et filter<br />
som 10 -5 til at afgøre om resten er<br />
lille nok.<br />
Hvis man nu ikke indenfor de første<br />
20 iterationer kan finde en rest som<br />
er lille nok opfører lommeregner<br />
tallet sig altså ikke rationalt. Man<br />
kan da undersøge om tallet i stedet<br />
skulle være en kvadratisk irrationalitet,<br />
dvs. om spektret ser ud til at<br />
være periodisk. Det sker i praksis ved<br />
at undersøge om en passende forskydning<br />
af spektret stemmer overens<br />
med det oprindelige spektrum.<br />
Hvis vi fx ser på spektret for tallet<br />
(9– 3 )/6, som er givet ved<br />
L1 = {1 4 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 …},<br />
så vil den to gange forskudte liste L1″<br />
L1″ = {1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 … }<br />
netop ende på samme måde som L1,<br />
idet differensen ender på lutter<br />
nuller:<br />
L1–L1″ = {0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0…}.<br />
Altså er spektret periodisk med<br />
perioden 2. Dermed har vi samlet<br />
ingredienserne til et program, som<br />
kan genkende simple typer af tal, og<br />
dermed udføre simple inverse symbolske<br />
udregninger.<br />
De ovenstående rutiner er samlet i<br />
programmet NICE, der findes til<br />
såvel TI-82, TI-83 som TI-86. Det<br />
adskiller sig fra Frac-rutinen på to<br />
forskellige måder: Dels kan det også<br />
genkende simple kvadratrodskombinationer,<br />
dels er det meget mere<br />
forsigtigt med at genkende rationale<br />
tal, idet det både checker om tallet<br />
opfører sig rationalt, og om det<br />
rationale tal genskaber alle cifrene<br />
indefor regnemaskinens nøjagtighed.<br />
Til gengæld er det selvfølgelig ikke så<br />
hurtigt som Frac-rutinen, da det jo<br />
skal fortolkes under udføreslen, i<br />
modsætning til Frac-rutinen, som jo<br />
er skrevet i maskinkode. Det skal<br />
derfor ikke opfattes som en erstatning<br />
for Frac-rutinen, men som et<br />
nyttigt supplement!