PÅÃKLADY K MATEMATICE 2 1. Funkce vÃce promÄnných 1.1 ...
PÅÃKLADY K MATEMATICE 2 1. Funkce vÃce promÄnných 1.1 ... PÅÃKLADY K MATEMATICE 2 1. Funkce vÃce promÄnných 1.1 ...
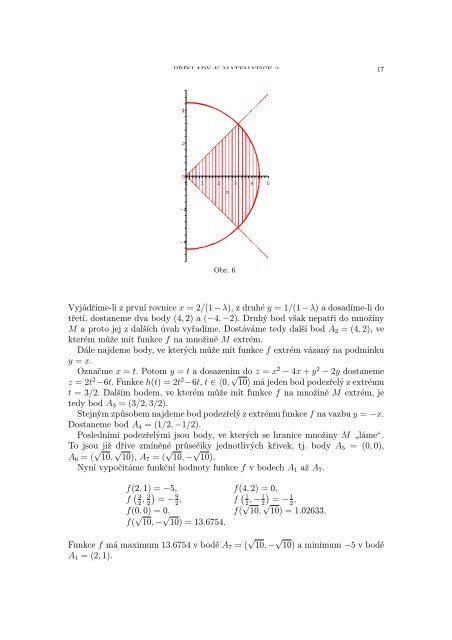
16 ZDENĚK ŠIBRAVAPříklad 1.63. f(x, y) = 3x − y, y = x 3 + 1.Výsledek: Ostré lok. max. f(1, 2) = 1, Ostré lok. min. f(−1, 0) = −3Příklad 1.64. f(x, y) = x 2 y, y = e x .Výsledek: Ostré lok. max. f(−2, e −2 ) = 4 e −2 , Ostré lok. min. f(0, 1) = 0Příklad 1.65. f(x, y) = 1 + 1 , 4x + y = 6 ∧ x ≠ 0 ∧ y ≠ 0.x yVýsledek: Ostré lok. max. f(3, −6) = 1/6, Ostré lok. min. f(1, 2) = 3/2Příklad 1.66. f(x, y) = x 2 − y 2 , x 2 + y 2 = 1.Výsledek: Ostrá lok. max. f(±1, 0) = 1, Ostrá lok. min. f(0, ±1) = −11.2.3. Globální extrémy funkcí dvou a tří proměnných.Příklad 1.67. Najděme globální extrémy funkce f(x, y) = x 2 − 4x + y 2 − 2y namnožině M = {(x, y) ∈ R 2 : x ≥ |y| ∧ x 2 + y 2 ≤ 20}.Řešení: Při hledání globálních (absolutních) extrémů spojité funkce f na uzavřenémnožině M budeme postupovat následujícím způsobem:(i) Najdeme všechny kritické body na M.(ii) Najdeme všechny kritické body funkce f vázané na hranici h množiny M.(iii) Najdeme všechny body, ve kterých se h „láme (ke křivce v tomto boděnelze sestrojit tečnu).(iv) Ve všech těchto nalezených bodech vypočítáme funkční hodnotu funkcef. Největší, resp. nejmenší z těchto hodnot je globální maximum, resp.globální minimum funkce f na množině M.V našem případě je množina M kruhová výseč o poloměru √ 20 se středemv počátku, ohraničená přímkami y = x a y = −x, přičemž x ≥ 0 (Obr. 6).Hledejme stacionární body funkce f.∂f(x,y)= 2x − 4, ⇒ 2x − 4 = 0,∂x∂f(x,y)= 2y − 2, ⇒ 2y − 2 = 0.∂yOdtud A 1 = (2, 1).Nyní najdeme kritické body na hranici h množiny M. Tato hranice je sjednocenímtří křivek C 1 (část kružnice x 2 + y 2 = 20), C 2 (část přímky y = x) a C 3(část přímky y = −x), přičemž tyto křivky se postupně protnou v bodech (0, 0),( √ 10, √ 10), ( √ 10, − √ 10).Body podezřelé z extrémů vazaných na podmínku x 2 + y 2 = 20 najdeme metodouLagrangeových multiplikátorů. Hledáme takový bod A = (x, y) (splňujícípodmínku g(x, y) = 0) a takový skalár λ, pro který platí∇f(A) = λ · ∇g(A).Protože ∇f(x, y) = (2x − 4, 2y − 2) a ∇g(x, y) = (2x, 2y), je A řešením soustavy2x − 4 − 2λx = 0,2y − 2 − 2λy = 0,x 2 + y 2 − 20 = 0.
PŘÍKLADY K MATEMATICE 2 174200 1 2 3 4 5x-2-4Obr. 6Vyjádříme-li z první rovnice x = 2/(1 − λ), z druhé y = 1/(1 − λ) a dosadíme-li dotřetí, dostaneme dva body (4, 2) a (−4, −2). Druhý bod však nepatří do množinyM a proto jej z dalších úvah vyřadíme. Dostáváme tedy další bod A 2 = (4, 2), vekterém může mít funkce f na množině M extrém.Dále najdeme body, ve kterých může mít funkce f extrém vázaný na podmínkuy = x.Označme x = t. Potom y = t a dosazením do z = x 2 − 4x + y 2 − 2y dostanemez = 2t 2 −6t. Funkce h(t) = 2t 2 −6t, t ∈ 〈0, √ 10〉 má jeden bod podezřelý z extrémut = 3/2. Dalším bodem, ve kterém může mít funkce f na množině M extrém, jetedy bod A 3 = (3/2, 3/2).Stejným způsobem najdeme bod podezřelý z extrému funkce f na vazbu y = −x.Dostaneme bod A 4 = (1/2, −1/2).Posledními podezřelými jsou body, ve kterých se hranice množiny M „láme.To jsou již dříve zmíněné průsečíky jednotlivých křivek, tj. body A 5 = (0, 0),A 6 = ( √ 10, √ 10), A 7 = ( √ 10, − √ 10).Nyní vypočítáme funkční hodnoty funkce f v bodech A 1 až A 7 .f(2, 1) = −5, f(4, 2) = 0,f ( 3, ) 32 2 = −9, f ( 1, − 12 2 2)= −12 ,f(0, 0) = 0, f( √ 10, √ 10) = 1.02633,f( √ 10, − √ 10) = 13.6754.Funkce f má maximum 13.6754 v bodě A 7 = ( √ 10, − √ 10) a minimum −5 v boděA 1 = (2, 1).
- Page 4 and 5: 4 ZDENĚK ŠIBRAVAkde ∇f(P ) je g
- Page 6 and 7: 6 ZDENĚK ŠIBRAVANechť tedy P = (
- Page 8 and 9: 8 ZDENĚK ŠIBRAVAa funkce f má v
- Page 10 and 11: 10 ZDENĚK ŠIBRAVAŘešení: Funkc
- Page 12 and 13: 12 ZDENĚK ŠIBRAVA12108z 642-4 -4-
- Page 14 and 15: 14 ZDENĚK ŠIBRAVA141210z8644-4-22
- Page 18 and 19: 18 ZDENĚK ŠIBRAVAPříklad 1.68.
- Page 20 and 21: 20 ZDENĚK ŠIBRAVAPříklad 1.70.
- Page 22: 22 ZDENĚK ŠIBRAVAPříklad 1.98.
PŘÍKLADY K <strong>MATEMATICE</strong> 2 174200 1 2 3 4 5x-2-4Obr. 6Vyjádříme-li z první rovnice x = 2/(1 − λ), z druhé y = 1/(1 − λ) a dosadíme-li dotřetí, dostaneme dva body (4, 2) a (−4, −2). Druhý bod však nepatří do množinyM a proto jej z dalších úvah vyřadíme. Dostáváme tedy další bod A 2 = (4, 2), vekterém může mít funkce f na množině M extrém.Dále najdeme body, ve kterých může mít funkce f extrém vázaný na podmínkuy = x.Označme x = t. Potom y = t a dosazením do z = x 2 − 4x + y 2 − 2y dostanemez = 2t 2 −6t. <strong>Funkce</strong> h(t) = 2t 2 −6t, t ∈ 〈0, √ 10〉 má jeden bod podezřelý z extrémut = 3/2. Dalším bodem, ve kterém může mít funkce f na množině M extrém, jetedy bod A 3 = (3/2, 3/2).Stejným způsobem najdeme bod podezřelý z extrému funkce f na vazbu y = −x.Dostaneme bod A 4 = (1/2, −1/2).Posledními podezřelými jsou body, ve kterých se hranice množiny M „láme.To jsou již dříve zmíněné průsečíky jednotlivých křivek, tj. body A 5 = (0, 0),A 6 = ( √ 10, √ 10), A 7 = ( √ 10, − √ 10).Nyní vypočítáme funkční hodnoty funkce f v bodech A 1 až A 7 .f(2, 1) = −5, f(4, 2) = 0,f ( 3, ) 32 2 = −9, f ( 1, − 12 2 2)= −12 ,f(0, 0) = 0, f( √ 10, √ 10) = <strong>1.</strong>02633,f( √ 10, − √ 10) = 13.6754.<strong>Funkce</strong> f má maximum 13.6754 v bodě A 7 = ( √ 10, − √ 10) a minimum −5 v boděA 1 = (2, 1).